ТЕОРИЯ МНОЖЕСТВ 1. Основные понятия теории множеств Множество – некоторая совокупность объектов, называемых элементами этого множества. Понятие множества является одн им из исходных (аксиоматических) понятий математики, то есть не сводимое к другим понятиям, а значит и не имеющее определения. Однако, можно дать описание множества. Основатель теории множеств - Георг Кантор, немецкий математик, 1845-1918.
В данном курсе рассматириваются конечные множества и бесконечные счетные множнства, т.е. такие множества элементы которых можно пересчитать с помощью натуральных чисел. Множества конечные, содержат конечное число элементов по числу содержащихся в них элементов делятся на 2 вида бесконечные, содержат конечное число элементов
1.1 Способы задания множеств Множества обозначают большими латинскими буквами : A, B, C,... Элементы множеств обозначают малыми латинскими буквами : a, b, c,... Если элемент a принадлежит множеству A, то пишут : a A Если элемент a не принадлежит множеству A, то пишут : a A
Способы задания множеств: 1. Множество А определяется перечислением всех своих элементов: V = {a, e, i, o, u, õ, ä, ö, ü} A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} 2. Множество А определяется частичным перечислением своих элементов, которое выражает какую-то определенную закономерность : Z = {..., -2, -1, 0, 1, 2, 3...} – множество целых чисел N = {0, 1, 2, 3,...}- множество натуральных чисел Пример : Пример :
3. Множество А определяется как совокупность элементов из множества Т, которые обладают свойством : А = х Т ( х ) , где запись ( х ) означает, что элемент х обладает свойством . B = { x N | x mod 2 = 0} – множество четных натуральных чисел C = { a N | a – простое число } – множество простых чисел D = { n N | n > 1000 & n < 2000} – множество натуральных чисел больших 1000, но меньших 2000 Пример :
1.2 Операции над множествами ( теоретико-множественные операции ) Равенство множеств: Множества A и B равны, если они состоят из одних и тех же элементов : {1, 3, 5} = {5, 1, 3} Подмножество: Множество A является подмножеством множества B, A B, если каждый элемент множества A принадлежит в то же время и множеству B : A B x ( x A x B ) А В диаграмм а Эйлера - Венна
Свойства : A ( A A ) ( A B ) & ( B A ) A = B по определению равенства множеств: A = B ( x, x A x B & x, x В x А ) Пустое множество является подмножеством любого множества : A ( A ) Пустое множество: Множество, которое не содержит ни одного элемента называется пустым множеством и обозначается символом = { }. Свойство :
Универсальное множество I : V = {a, e, i, o, u, õ, ä, ö, ü} – множество гласных букв I = { множество всех букв } V Каждое множество A является подмножеством универсального множества : A ( A I ) Множество, которое содержит все возможные элементы, рассматриваемые в данном контексте. Пример : I
Дополнение множества: Элементы универсального множества I, не принадлежащие к множеству A, образуют дополнение множества A относительно универсального множества I, которое обозначают A I = {E, T, K, N, R, L, P} A = {L, P} A = {E, T, K, N, R} A A I A = { x I | x A} Пример : дни недели делятся на будничные и выходные дни
Объединение (сумма) множеств: A B = { x x A или x B } = A + B Пример : {1, 4, 7} {2, 4, 6, 7 } = { 1, 2, 4, 6, 7} Объединение множеств А и В состоит из элементов, принадлежащих хотя бы одному из множеств А или В : A B I
A B = { x x A и x B } = AB Пример : {1, 4, 7} {2, 4, 6, 7 } = {4, 7} Пересечение (общая часть, умножение) множеств: Пересечение множеств А и В состоит из элементов, принадлежащих одновременно множеству А и множеству В : A B I A B
Непересекающиеся множества: Если A B = , то множества A и B непересекающиеся множества. {1, 4, 7} {2, 3, 6} = Пример :
A \ B = { x x A и x B } Пример : {1, 4, 7} \ {2, 4, 6, 7 } = { 1 } Разность множеств: Разность множеств А и В состоит из элементов, принадлежащих множеству А и не принадлежащих множеству В: A B I
Симметрическая разность множеств: Симметрическая разность множеств A и B состоит из элементов принадлежащих множеству А или множеству В, но не принадлежащих множествам А и В одновременно : A B I A B = { x ( x A ) & ( x B ) ( x A ) & ( x B ) } Пример : {1, 4, 7} {2, 4, 6, 7 } = { 1, 2, 6 }
Приоритет выполнения операций Сначала выполняются операции дополнения, затем пересечения, объединения, разности и симметрической разности которые имеют одинаковый приоритет. Последовательность выполнения операций может быть изменена скобками. Если в выражении есть знаки пересечения и объединения и нет скобок, то сначала выполняется операция пересечения, а потом – операция объединения (аналог сложению и умножению в арифметике).
Определение 1.3.1 выражение теории множеств определяется следующим образом : Все множества A, B,... - выражения теории множеств ; Пустое множество и универсальное множество I - выражения (константы) теории множеств ; Если A – выражение теории множеств, то A – тоже выражение теории множеств ; Если A и B - выражения теории множеств, то A B, A B, A \ B, A B – тоже выражения теории множеств. При помощи теоретико-множественны х операци й из множеств образуют выражения. 1.3 Выражение теории множеств
Свойства теоретико-множественны х операци й 2. Коммутативность: a) A B = B b) A B = B 3. Асоциативность: a) A ( B C ) = ( A B ) C b) A ( B C ) = ( A B ) C 4. Дистрибутивность: a) A ( B C ) = ( A B ) ( A C ) b) A ( B C ) = ( A B ) ( A C ) 5. Идемпотентность: a) A A = A b) A A = A 1.
6. Действия с константами : 7. Законы де Моргана : 8. Преобразование разности : A \ B = A B 9. Преобразования симметрической разности : A B = (A \ B) (B \ A) A B = (A B) \ (A B) 10. Законы склеивания : (A B) (A B) = A (A B) (A B) = A 11. Законы поглощения : A (A B) = A A (A B) = A A I = I A A = I A A = A = A = A A I = A
1.4 Нормальные формы Кантора ( НФК ) Нормальной формой Кантора ( НФК ) выражения теории множеств называют выражение, которое представляет собой пересечение объединений или объединение пересечений. Пересечение объединений в теории множеств аналогично КНФ в мат. логике. ( A B ) ( A C ) ( A B ) ( A C ) Дополнение в нормальной форме может быть применено только к отдельным множествам, не к их объединению или пересечению. Объединие пересечений в теории множеств аналогично ДНФ в мат. логике.
Совершенной нормальной формой Кантора ( СНФК ) выражения теории множеств называют такое пересечение объединений или объединение пересечений, где в каждом пересечении/объединении присутствует каждое множество выражения и точно один раз.
Задача 1. Доказать равенство выражений теории множеств : А) B) C) D)
Задача 2. Найти СНФК : А) B) C) D)
Задача 3. Найти МНФК : A) H(A,B,C)= ( 0, 2, 3, 4, 6 ) B) H(A,B,C,D)= ( 0, 1, 4, 5, 8,9,14 ) C) H(A,B,C,D)= ( 1, 3, 4, 5, 7,8,9,11,12,15 )
A B C = A + B + C - A B - A C - B C + + A B C 1.5. Мощность множеств. Формулы Грассмана Мощностью конечного множества A называют количеств о (числ о ) элементов этого множества и обозначают A . Формулы Грассмана позволяют найти мощность объединения множеств : A B = A + B - A B
Задача 4. Множество A состоит из натуральных чисел от 1 до 1000. Сколько элементов множества A не делится ни на 3, ни на 5. В группе 25 студентов. Для допуска к экзамену необходимо получить зачет по двум контрольным работам. По первой контрольной работе зачет получили 20 студентов, по второй 21. Сколько студентов (минимум и максимум) будет допущено к сдаче экзамена. Задача 5. Задача 6. Каждый студент физико-математического факультета интересуется физикой или математикой. Сколько студентов интересуется и физикой, и математикой, если математикой интересуется 84%, а физикой 64% студентов.
По результатам опроса 100 студентов 28 из них интересуется искусством, 30 музыкой, 42 спортом. 10 студентов интересуются и искусством, и спортом. 5 студентов интересуются и искусством, и музыкой. 8 студентов интересуются и спортом, и музыкой. 3 студента интересуется и искусством, и музыкой, и спортом. Сколько студентов интересуются только спортом? Только музыкой? Ничем из перечисленного? Задача 7.
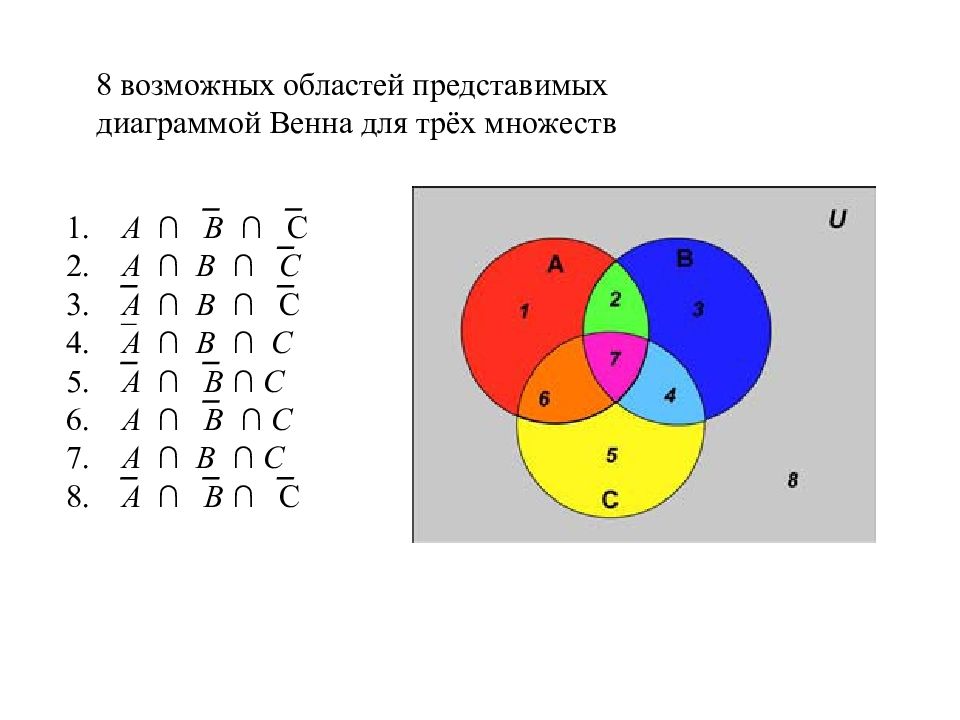
1. A ∩ B ∩ C 2. A ∩ B ∩ C 3. A ∩ B ∩ C 4. A ∩ B ∩ C 5. A ∩ B ∩ C 6. A ∩ B ∩ C 7. A ∩ B ∩ C 8. A ∩ B ∩ C 8 возможных областей представимых диаграммой Венна для трёх множеств
1.6. Прямое произведение множеств Прямое произведение множеств А и В состоит из упорядоченных пар элементов этих множеств А x B = { ( a, b ) | ( a A ) & ( b B ) } Свойства : A x B B x A | A x B | = | A | x | B | Пример : A = { a,b,c } B = {1,2} A x B = { ( a,1 ), ( a,2 ), ( b,1 ), ( b,2 ), ( c,1 ), ( c,2 ) }
Множество всех подмножеств множества A называется булеаном A или степенью множества A, и обозначается Р(А) или 2 A. A x B x C x D x … x Y = {( a, b, c, d, …, y ) | a A, b B,..., y Y} Прямое произведение нескольких множеств: A x А x ……. x А = А k – Декартова степень множества А k раз R x R = R 2 – ху-плоскость R x R x R = R 3 – xyz- пространство Пример :
