Для управления реляционными данными были введены реляционные языки обработки данных – реляционную алгебру и реляционное исчисление. Реляционная алгебра определяет следующие операции: Объединение, Пересечение, Разность, Декартово произведение, Выбор (селекция), Проекция, Естественное соединение, Деление.
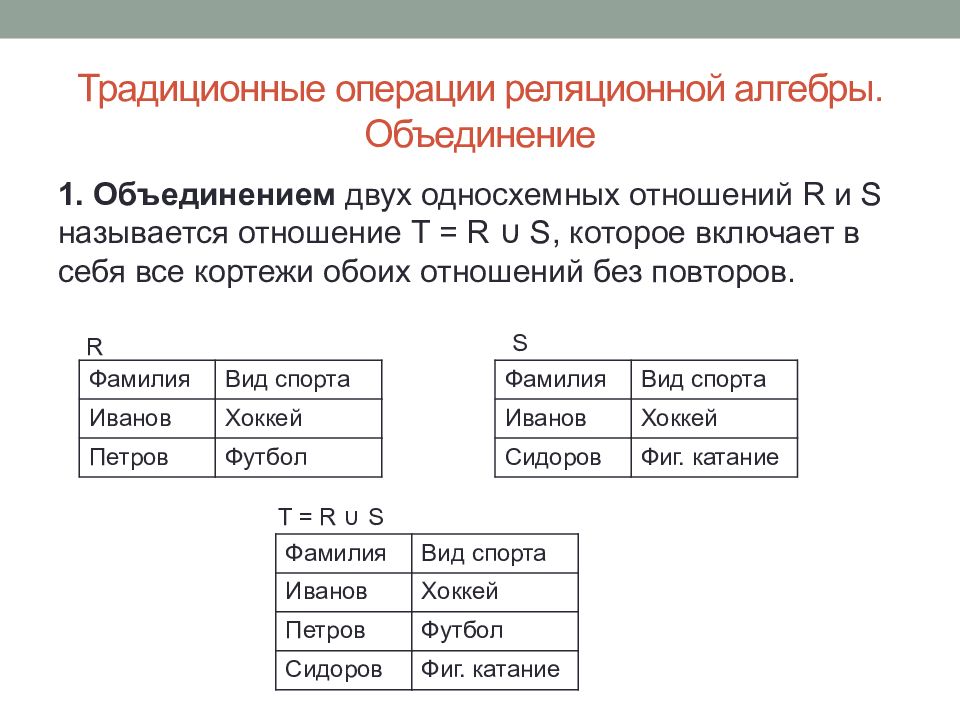
1. Объединением двух односхемных отношений R и S называется отношение T = R ∪ S, которое включает в себя все кортежи обоих отношений без повторов. Фамилия Вид спорта Иванов Хоккей Петров Футбол Фамилия Вид спорта Иванов Хоккей Сидоров Фиг. катание Фамилия Вид спорта Иванов Хоккей Петров Футбол Сидоров Фиг. катание R S T = R ∪ S
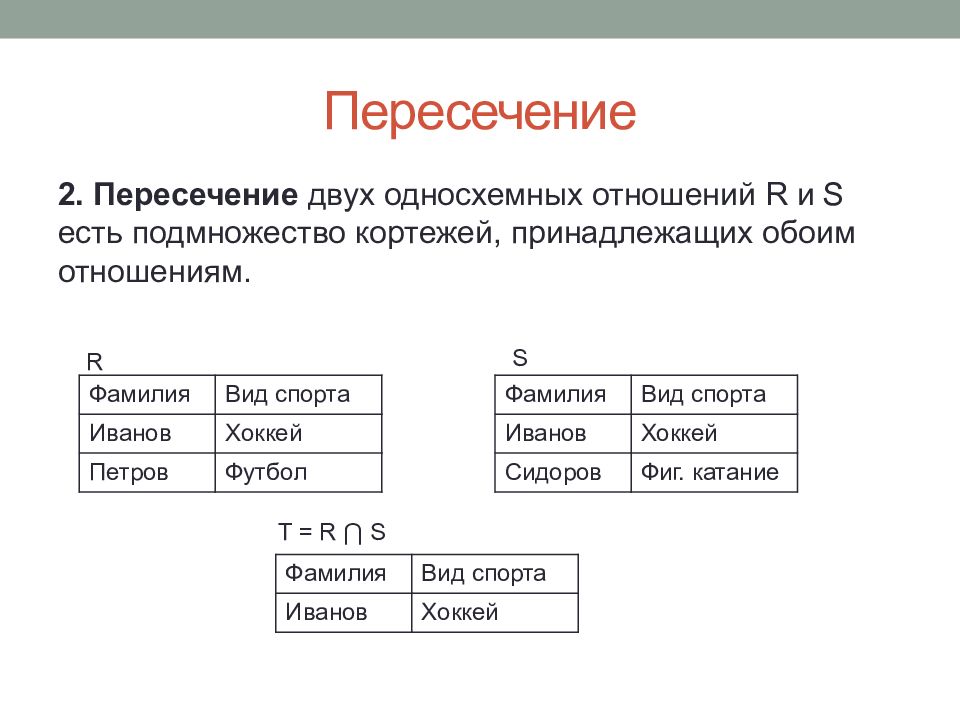
2. Пересечение двух односхемных отношений R и S есть подмножество кортежей, принадлежащих обоим отношениям. Фамилия Вид спорта Иванов Хоккей Петров Футбол R S Фамилия Вид спорта Иванов Хоккей Сидоров Фиг. катание T = R ⋂ S Фамилия Вид спорта Иванов Хоккей
3. Пусть имеется 2 отношения R и S, тогда отношение T = R - S называется разностью R и S, если каждый картеж, принадлежащий T принадлежит R, но не принадлежит S. R S Фамилия Вид спорта Иванов Хоккей Петров Футбол Фамилия Вид спорта Иванов Хоккей Сидоров Фиг. катание T = R - S Фамилия Вид спорта Петров Футбол
4. Операция декартова произведения ( R×S ) определяет новое отношение T, которое является результатом конкатенации каждого кортежа отношения R с каждым кортежем отношения S. Пусть имеются отношение R(A,B) и отношение S(C,D,E). Тогда декартово произведение R×S будет таким : A B a b b a c d C D E 1 2 3 4 5 6 A B C D E a b 1 2 3 a b 4 5 6 b a 1 2 3 b a 4 5 6 c d 1 2 3 c d 4 5 6 R S T = R× S
5. Селекция - это операция, результатом которой является подмножество кортежей исходного отношения, соответствующих условиям, которые накладываются на значения определённых атрибутов. Для отношения R(A,B,C) селекция sC =d(R) (при условии "значение атрибута C равно d") будет такой: A B C a b c c a d c b d A B C c a d c b d sC =d(R) R
6. Проекция - э то операция (выполняемая над одним отношением), служащая для выбора подмножества атрибутов из отношения R. Она уменьшает арность отношения и может уменьшить мощность отношения за счёт исключения одинаковых кортежей. R A B C a b c c a d c b d A C a d c d pA,C (R)
7. Естественное соединение ( join ) – операция возвращает отношение, картежи которого в сочетании двух картежей, принадлежащих соответственно двум исходным отношениям, имеющим общие атрибуты этих двух отношений. Новое отношение формируется путем сцепления картежей 1-го отношения с картежами 2-го отношения. A B C a b c c a d c h c g b d R A D E g h a c b c h d d S T = R join S A B C D E c a d b c c h c b c g b d h a
8. Пусть отношение R содержит атрибуты {r1,r2,..., rk, rk+1,..., rn }, а отношение S – атрибуты {rk+1,..., rn }. Тогда результирующее отношение содержит атрибуты {r1,r2,..., rk }. Кортеж отношения R включается в результирующее отношение, если его декартово произведение с отношением S входит в R A B C D a b c b c f g h a v c b a b g h c v g h c f c b R S C D g h c b A B a b c f R/S
