Первый слайд презентации: Векторная алгебра
Термин вектор (от лат. Vector - “ несущий “) впервые появился в 1845 г. у ирландского математика Уильяма Гамильтона Уи́льям Ро́уэн Га́мильтон 1805 — 1865 выдающийся ирландский математик и физик XIX века.
Слайд 2
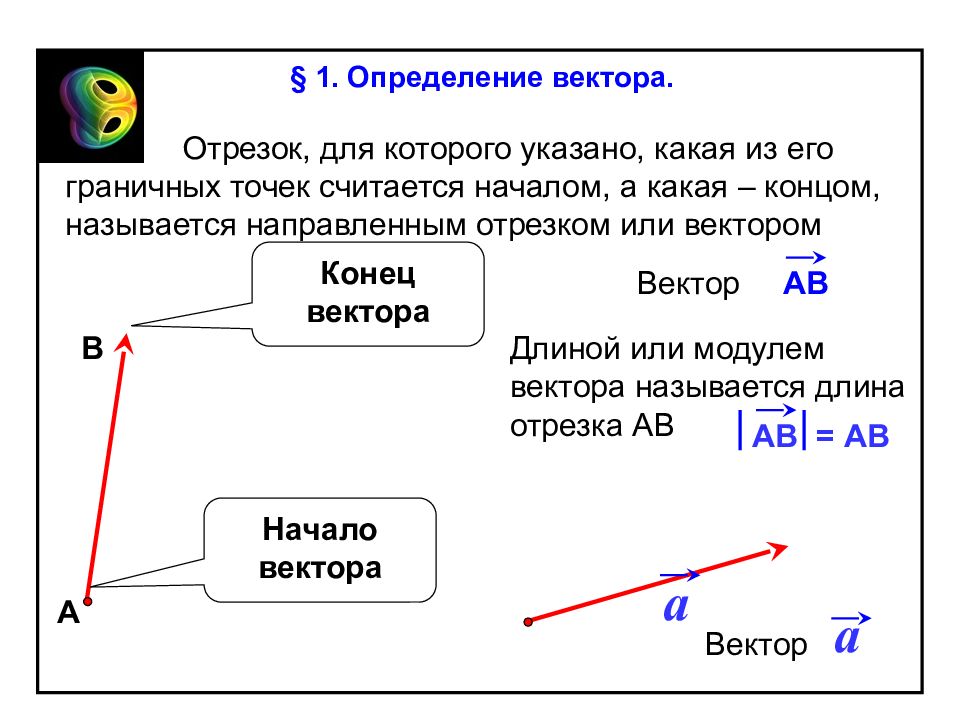
Длиной или модулем вектора называется длина отрезка АВ Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором А В a АВ = АВ Начало вектора Конец вектора АВ Вектор a Вектор § 1. Определение вектора.
Слайд 3
Любая точка плоскости также является вектором. В этом случае вектор называется нулевым M MM = 0 Длина нулевого считается равной нулю MM Вектор 0 Вектор Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определенного направления. Иначе говоря, любое направление можно считать направлением нулевого вектора. § 1. Определение вектора.
Слайд 4
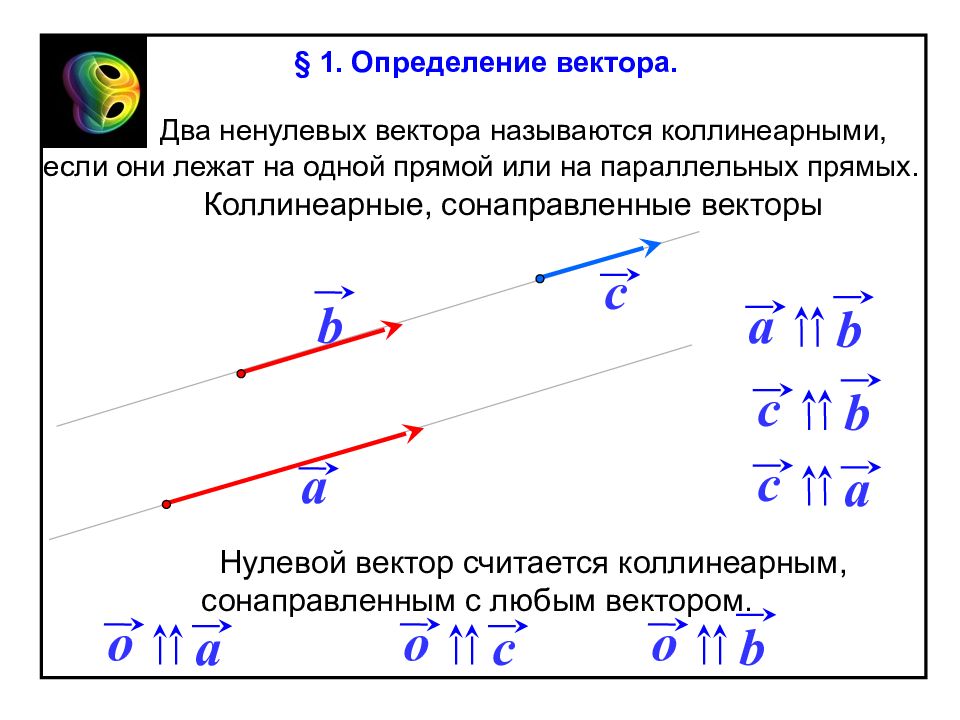
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. a b c a b c a c b Коллинеарные, сонаправленные векторы o a o c o b Нулевой вектор считается коллинеарным, сонаправленным с любым вектором. § 1. Определение вектора.
Слайд 5
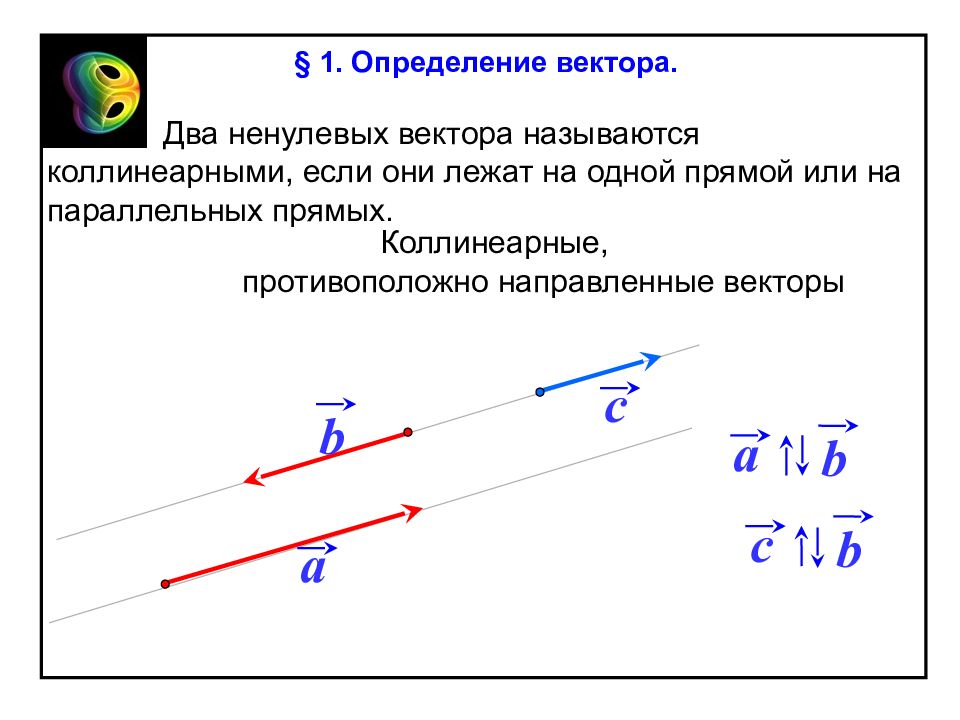
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. a b c b a Коллинеарные, противоположно направленные векторы b c § 1. Определение вектора.
Слайд 6
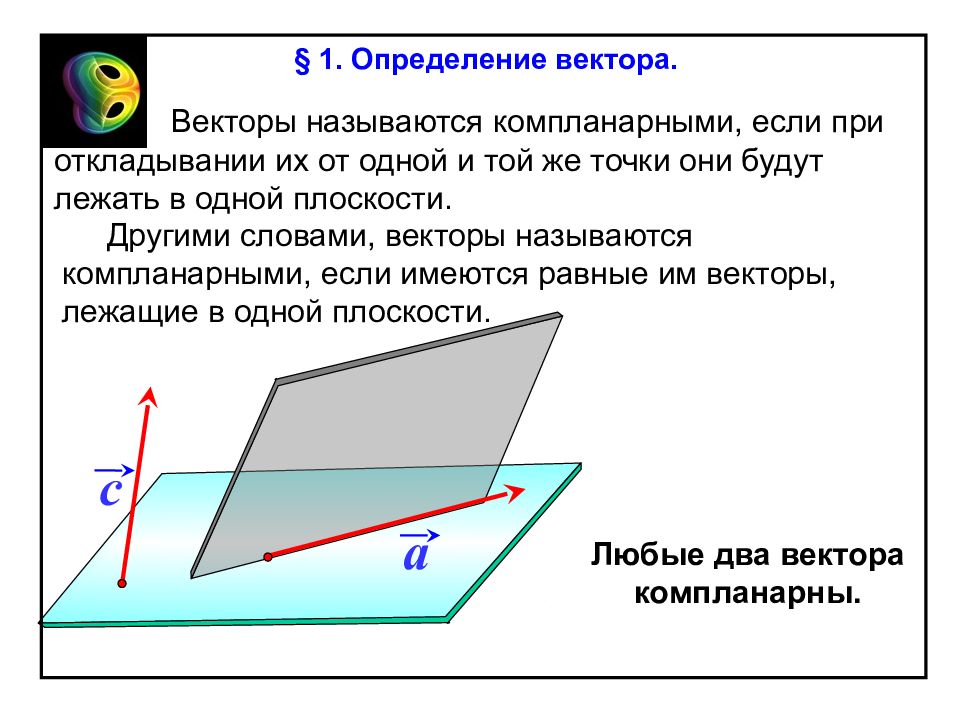
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Другими словами, векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости. a c Любые два вектора компланарны. § 1. Определение вектора.
Слайд 7
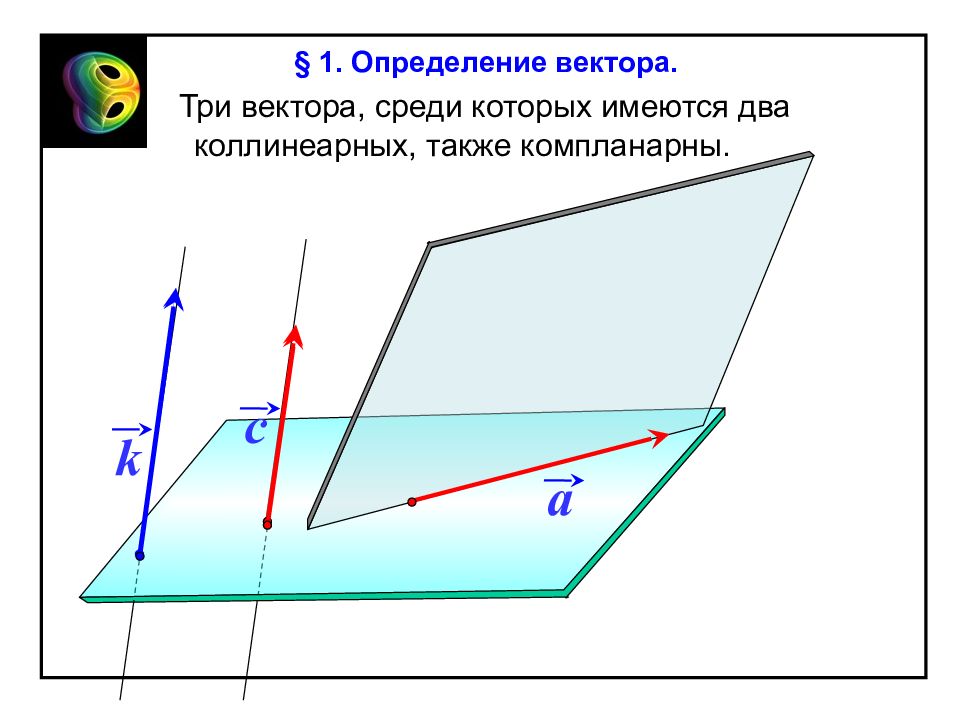
Три вектора, среди которых имеются два коллинеарных, также компланарны. c a k § 1. Определение вектора.
Слайд 8
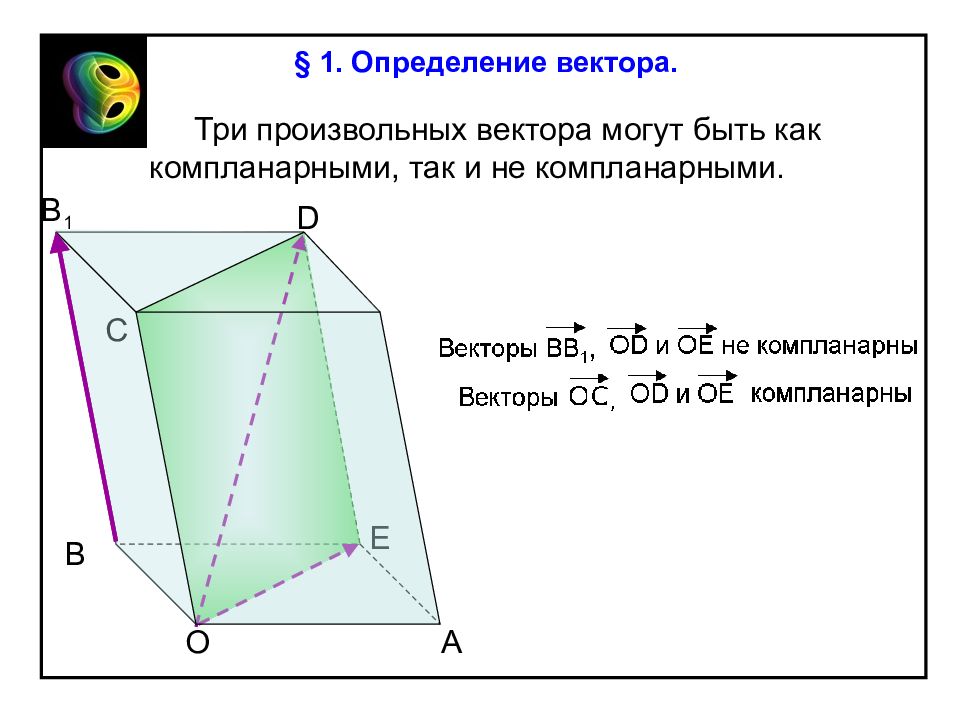
Три произвольных вектора могут быть как компланарными, так и не компланарными. А О Е D C В B 1 § 1. Определение вектора.
Слайд 9
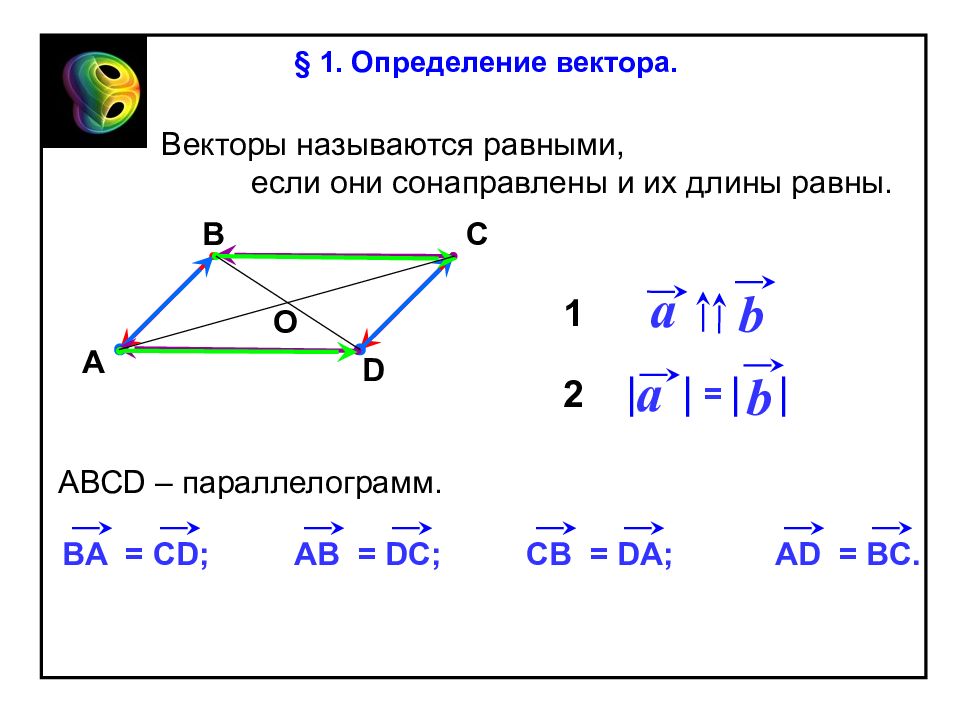
АВС D – параллелограмм. А В С D b a Векторы называются равными, если они сонаправлены и их длины равны. a b = 1 2 В A = CD ; A В = DC ; C В = DA ; AD = BC. О § 1. Определение вектора.
Слайд 10
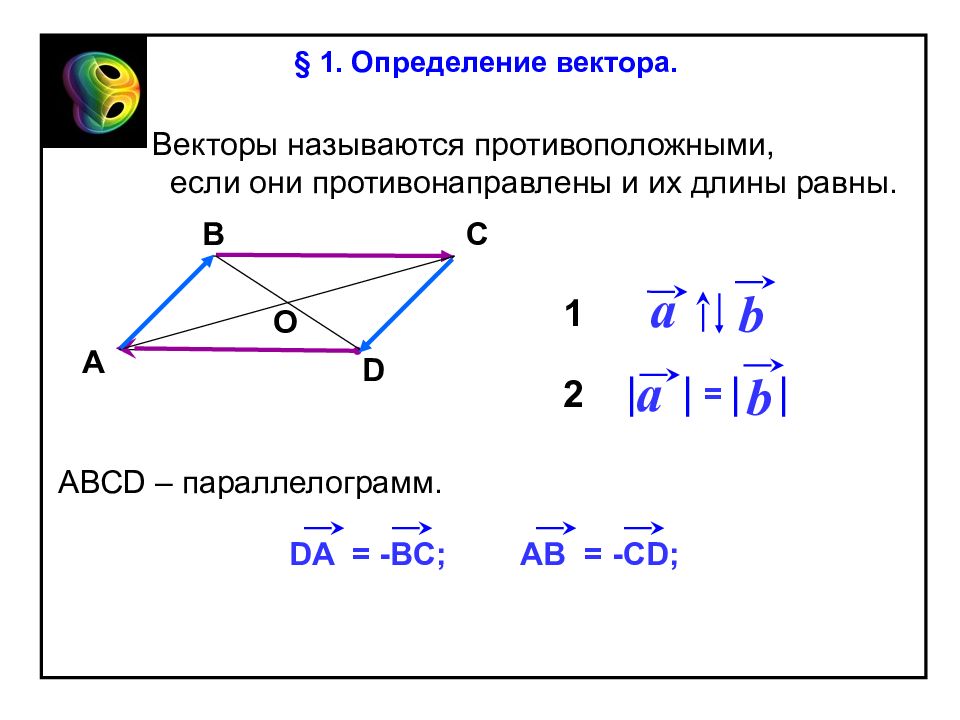
Векторы называются противоположными, если они противонаправлены и их длины равны. § 1. Определение вектора. АВС D – параллелограмм. А В С D b a a b = DA = - BC ; A В = - CD ; О 1 2
Слайд 11
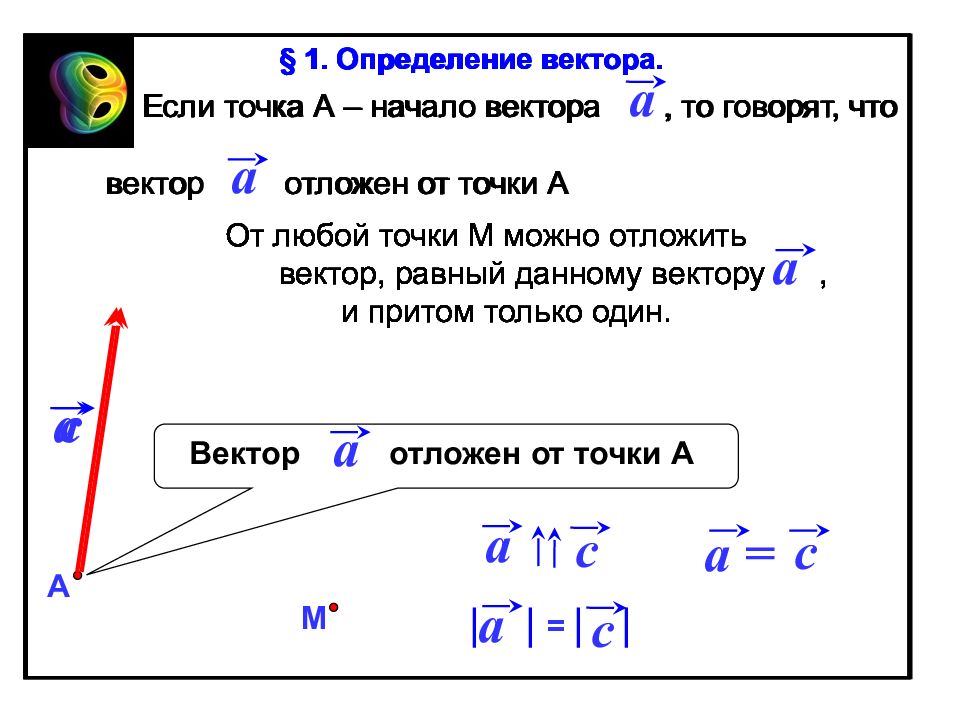
Если точка А – начало вектора, то говорят, что вектор отложен от точки А А a a Вектор отложен от точки А a a М c От любой точки М можно отложить вектор, равный данному вектору, и притом только один. a a c = c a c a = § 1. Определение вектора. Если точка А – начало вектора, то говорят, что вектор отложен от точки А § 1. Определение вектора. От любой точки М можно отложить вектор, равный данному вектору, и притом только один. Если точка А – начало вектора, то говорят, что вектор отложен от точки А § 1. Определение вектора. От любой точки М можно отложить вектор, равный данному вектору, и притом только один. Если точка А – начало вектора, то говорят, что вектор отложен от точки А § 1. Определение вектора. От любой точки М можно отложить вектор, равный данному вектору, и притом только один. От любой точки М можно отложить вектор, равный данному вектору, и притом только один. Если точка А – начало вектора, то говорят, что вектор отложен от точки А От любой точки М можно отложить вектор, равный данному вектору, и притом только один.
Слайд 12
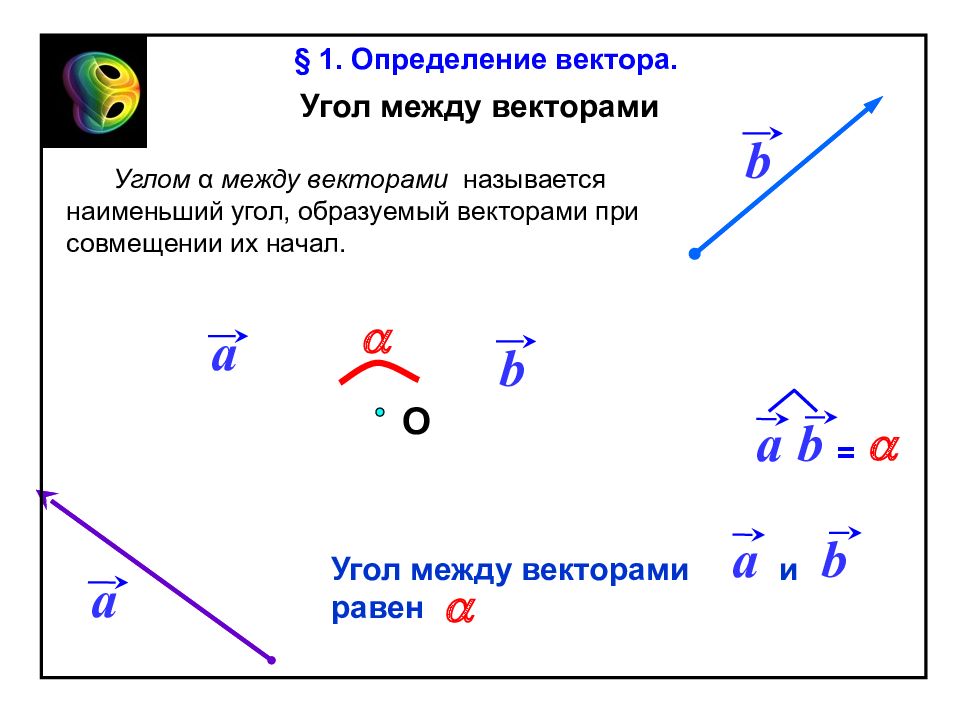
a b Угол между векторами a b a b a = a Угол между векторами и равен a a b О Углом α между векторами называется наименьший угол, образуемый векторами при совмещении их начал. § 1. Определение вектора.
Слайд 13
Два вектора называются ортогональными, если угол между ними равен 90 0. b c ^ Для коллинеарных векторов или b c § 1. Определение вектора.
Слайд 14
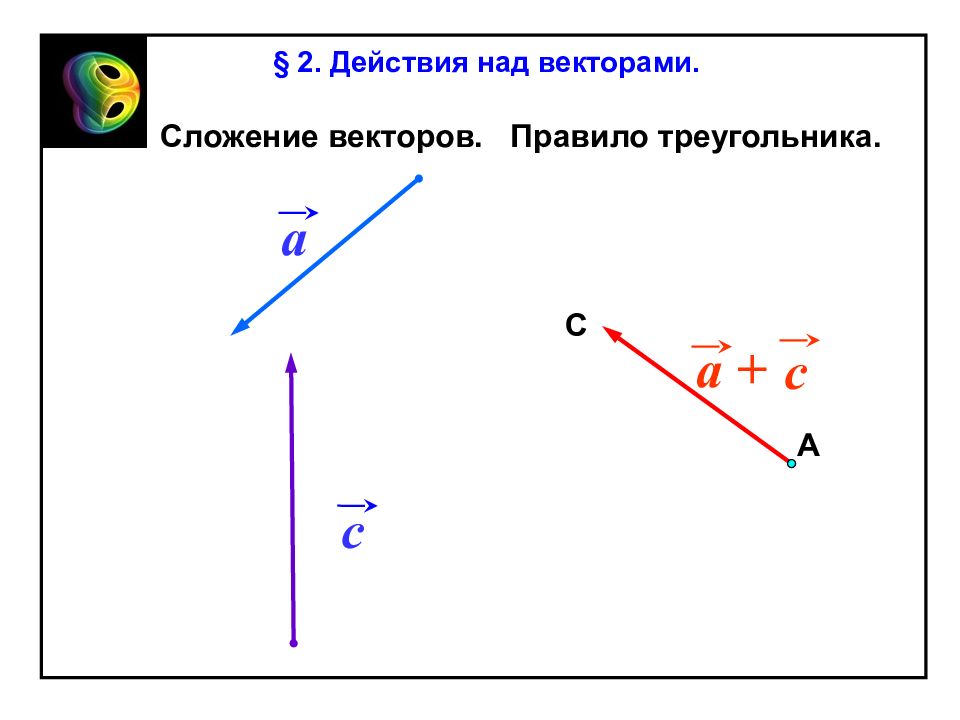
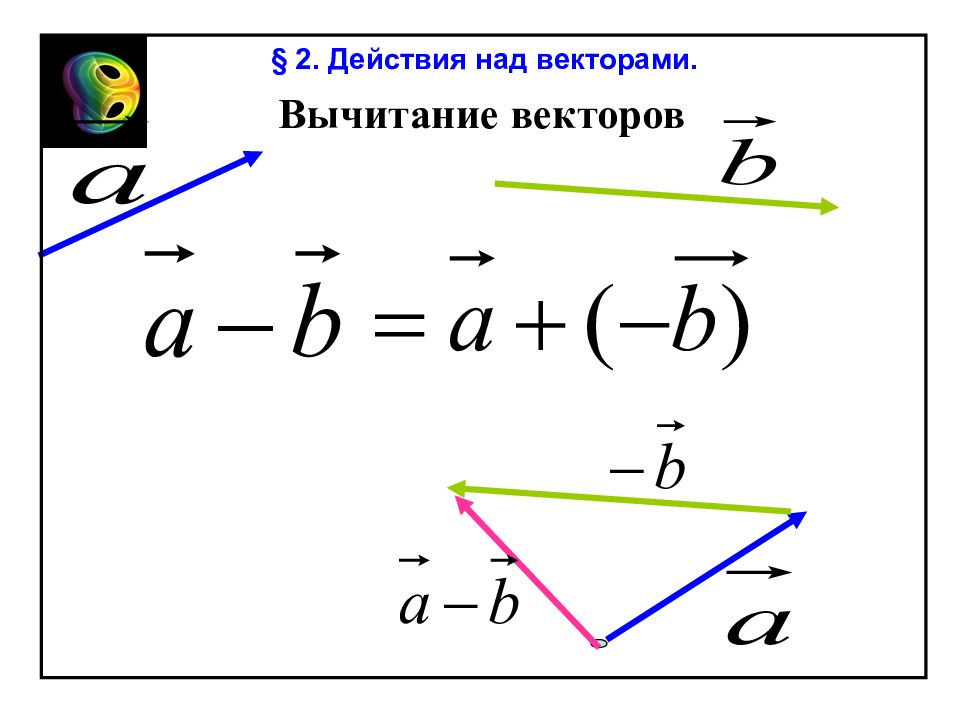
c a + a С А c Сложение векторов. Правило треугольника. § 2. Действия над векторами.
Слайд 15
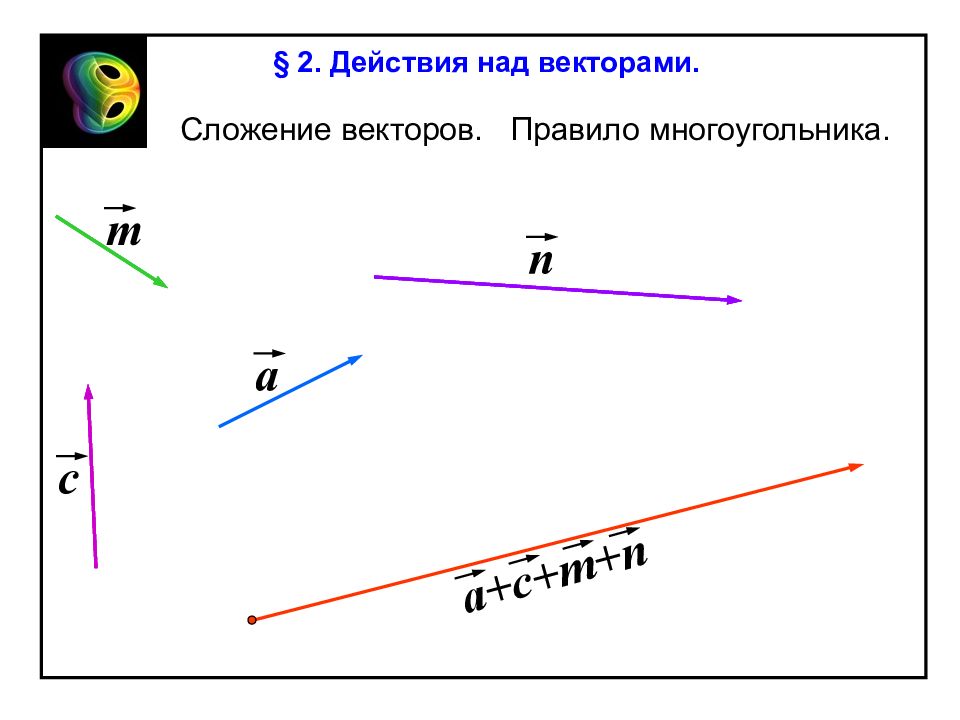
a c n m a+c+m+n Сложение векторов. Правило многоугольника. § 2. Действия над векторами.
Слайд 16
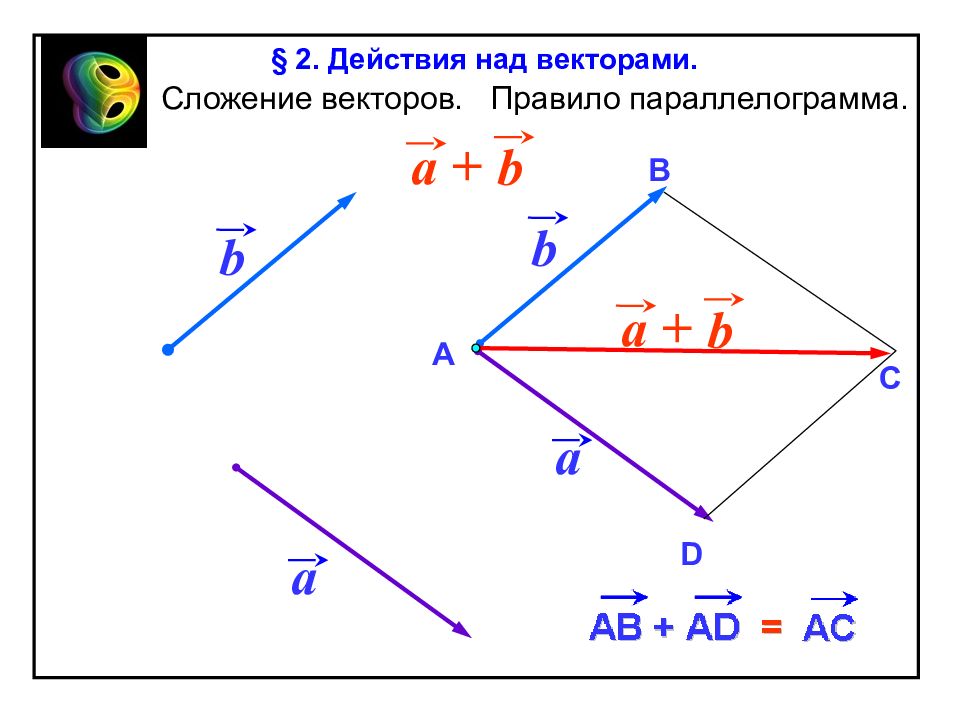
Сложение векторов. Правило параллелограмма. a a b b a + b b a + А В D C § 2. Действия над векторами.
Слайд 17
Сложим первые две силы F 1 и F 2 (аксиома параллелограмма). Количество сил уменьшилось на единицу. Сложим полученную равнодействующую R 12 со следующей силой F 3. Количество сил вновь уменьшилось на единицу. Повторим эту же операцию со следующей силой F 4. Осталась всего одна сила, эквивалентная исходной системе сил. Сложение сил построением параллелограммов можно заменить построением силового треугольника – выбирается одна из сил или изображается параллельно самой себе с началом в любой произвольной точке, все другие силы изображаются параллельными самим себе с началом, совпадающим с концом предыдущей силы. Результатом такого сложения является вектор, направленный из начала первой силы к концу последней из сил. § 2. Действия над векторами.
Слайд 18
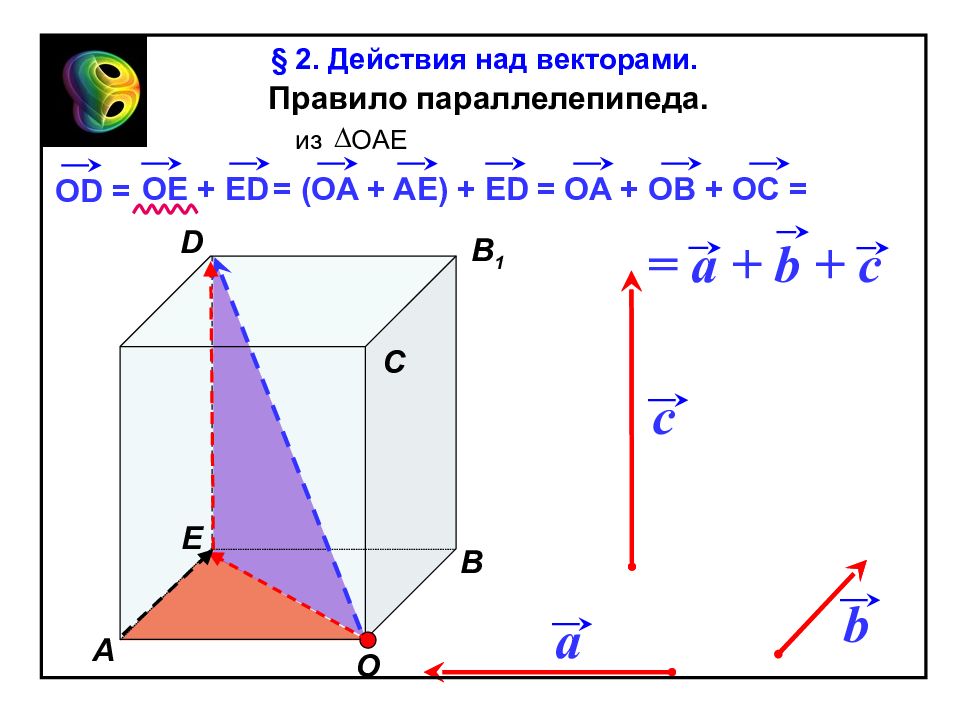
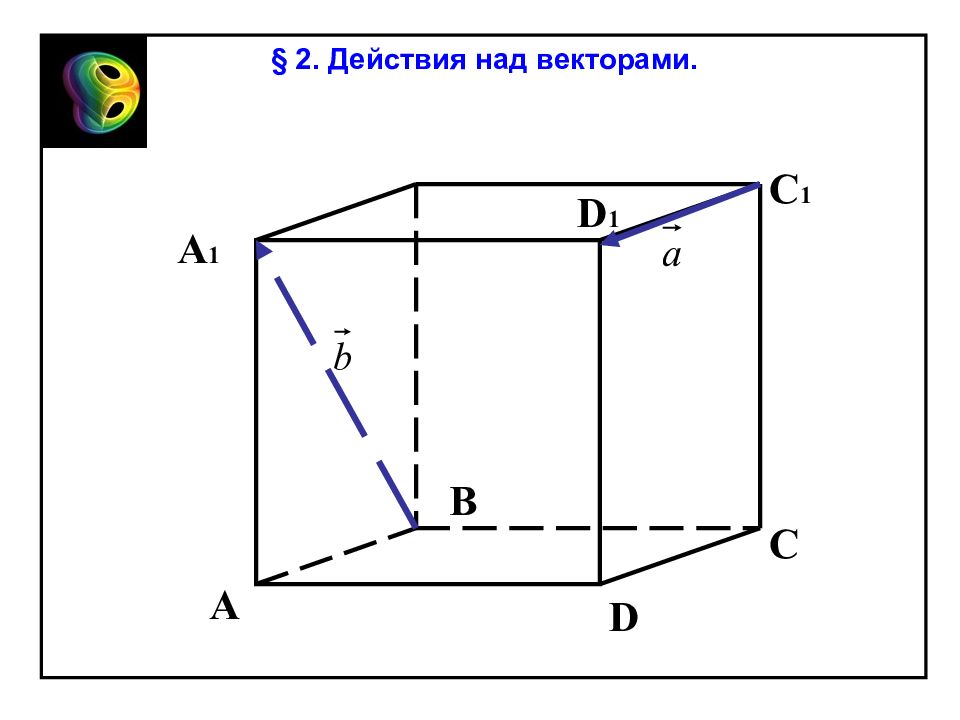
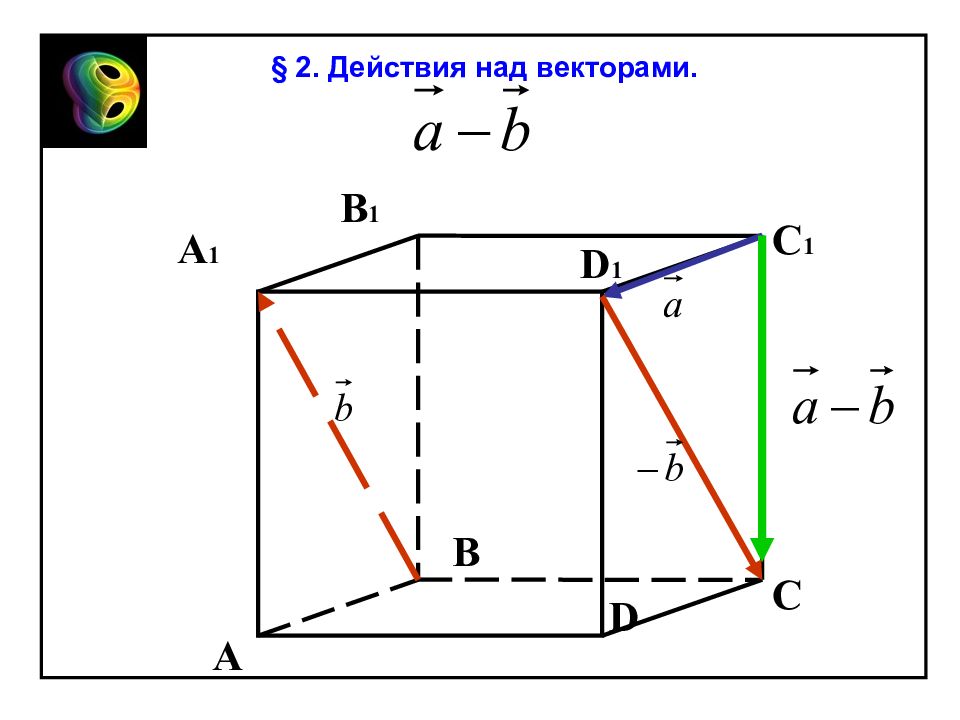
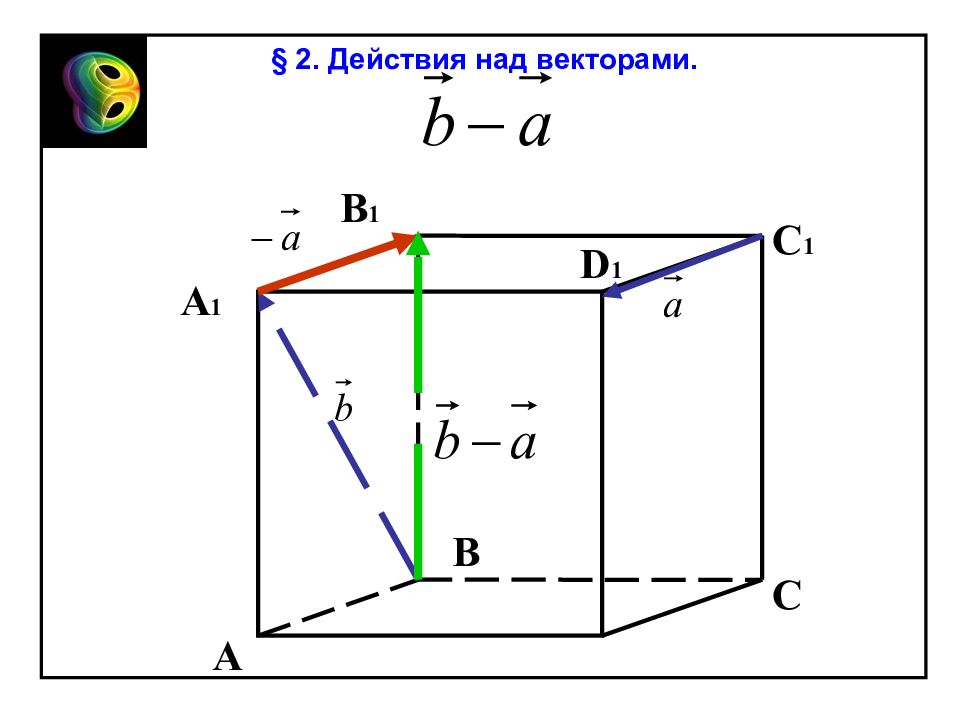
A В С В 1 D Е Правило параллелепипеда. a b c О OE + ED = (OA + AE) + ED = OA + OB + OC = = a + b + c из OAE OD = § 2. Действия над векторами.
Слайд 20
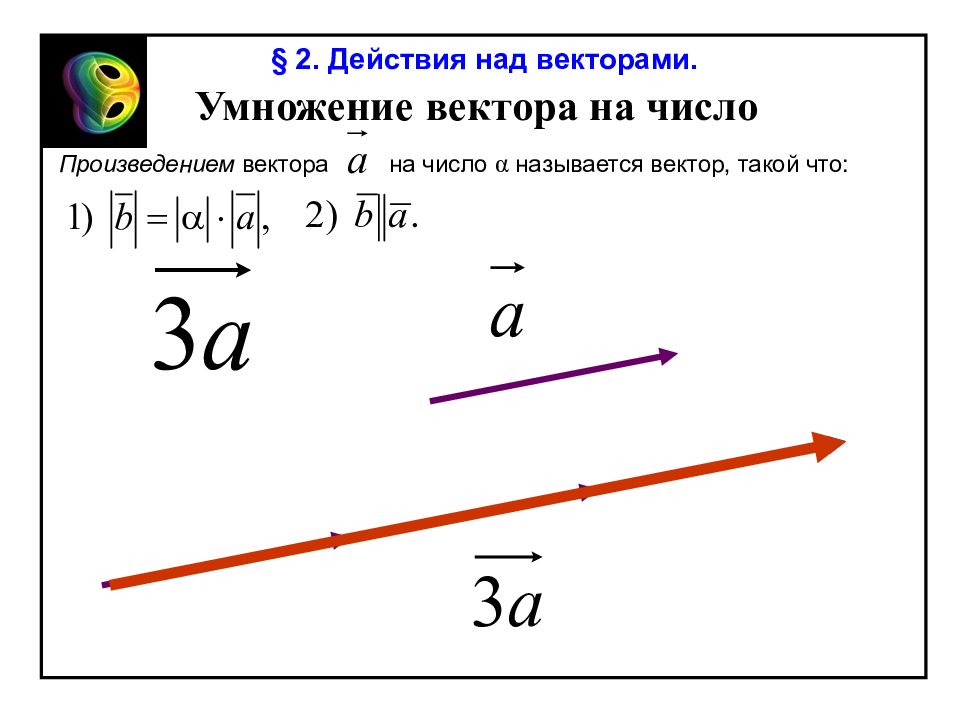
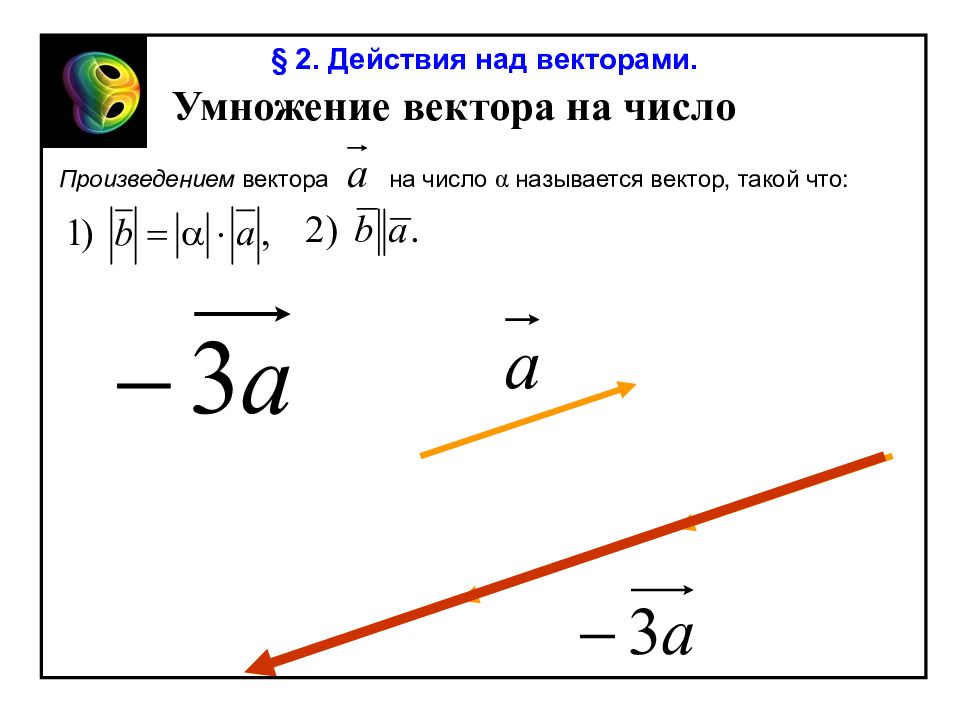
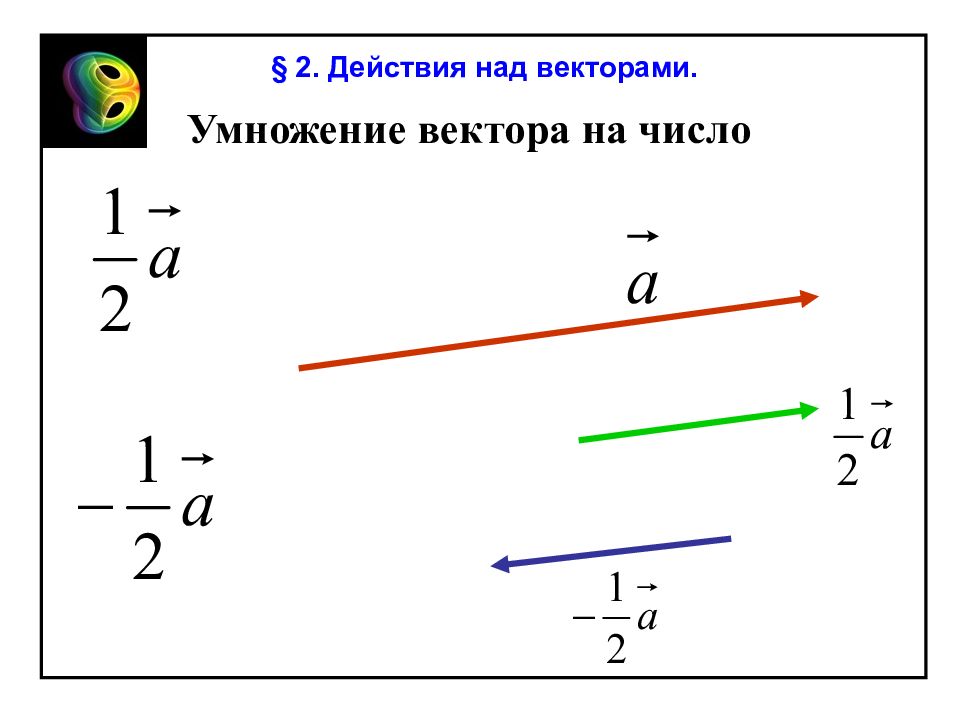
§ 2. Действия над векторами. Умножение вектора на число Произведением вектора на число α называется вектор, такой что:
Слайд 21
§ 2. Действия над векторами. Умножение вектора на число Произведением вектора на число α называется вектор, такой что:
Слайд 26
§ 3. Линейная зависимость векторов Определение 1. Линейной комбинацией векторов называется вектор где λ i – некоторые числа. Определение 2. Вектора называются линейно зависимыми, если существуют действительные числа λ i, такие, что хотя бы одно из них отлично от нуля, и при этом выполняется равенство: Определение 2. Вектора называются линейно независимыми, если из условия следует тривиальная комбинация
Слайд 27
§ 3. Линейная зависимость векторов Теорема 1. Для линейной зависимости векторов необходимо и достаточно, чтобы один из них был линейной комбинацией остальных. Доказательство. Необходимость. Пусть вектора линейно зависимы. Тогда существуют числа λ i, не равные нулю одновременно, такие, что Пусть λ 1 ≠ 0, тогда что доказывает необходимость. Достаточность. Пусть для определенности Тогда причем Это и есть условие линейной зависимости.
Слайд 28
§ 3. Линейная зависимость векторов Для линейно зависимых векторов справедливы теоремы 2–6. Теорема 2. Один вектор линейно зависим тогда и только тогда, когда он нулевой. Теорема 3. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Теорема 4. Три вектора линейно зависимы тогда и только тогда, когда они компланарны. Доказательство. Необходимость. Пусть три вектора линейно зависимы. Тогда существуют не равные одновременно нулю три числа, такие, что Тогда по теореме 1 один из векторов есть линейная комбинация двух остальных, и, значит, данные три вектора компланарны.
Слайд 29
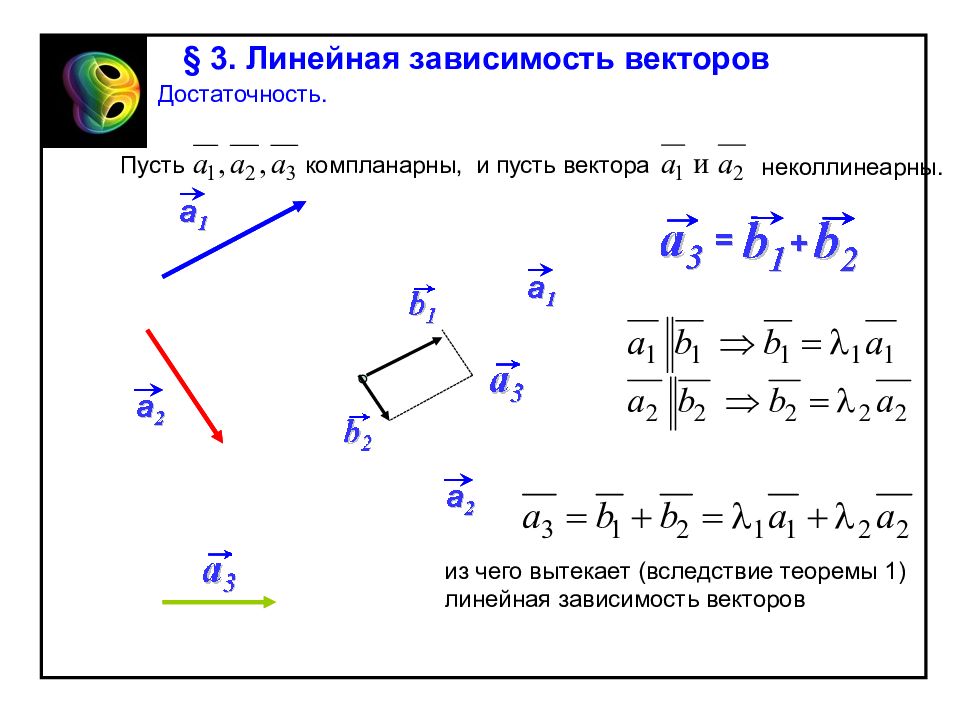
§ 3. Линейная зависимость векторов Достаточность. Пусть компланарны, и пусть вектора неколлинеарны. из чего вытекает (вследствие теоремы 1) линейная зависимость векторов
Слайд 30
§ 3. Линейная зависимость векторов Теорема 5. Любые четыре вектора в пространстве линейно зависимы. Действительно, можно подобрать, причем единственным образом, такие числа что будет Теорема 6. Если среди векторов имеется хотя бы один нулевой вектор, то вектора линейно зависимы.
Слайд 31
§ 3. Линейная зависимость векторов Свойства линейно независимых векторов: Один вектор линейно независим тогда и только тогда, когда он ненулевой. Два вектора линейно независимы тогда и только тогда, когда они неколлинеарны. Три вектора линейно независимы тогда и только тогда, когда они некомпланарны.
Слайд 32
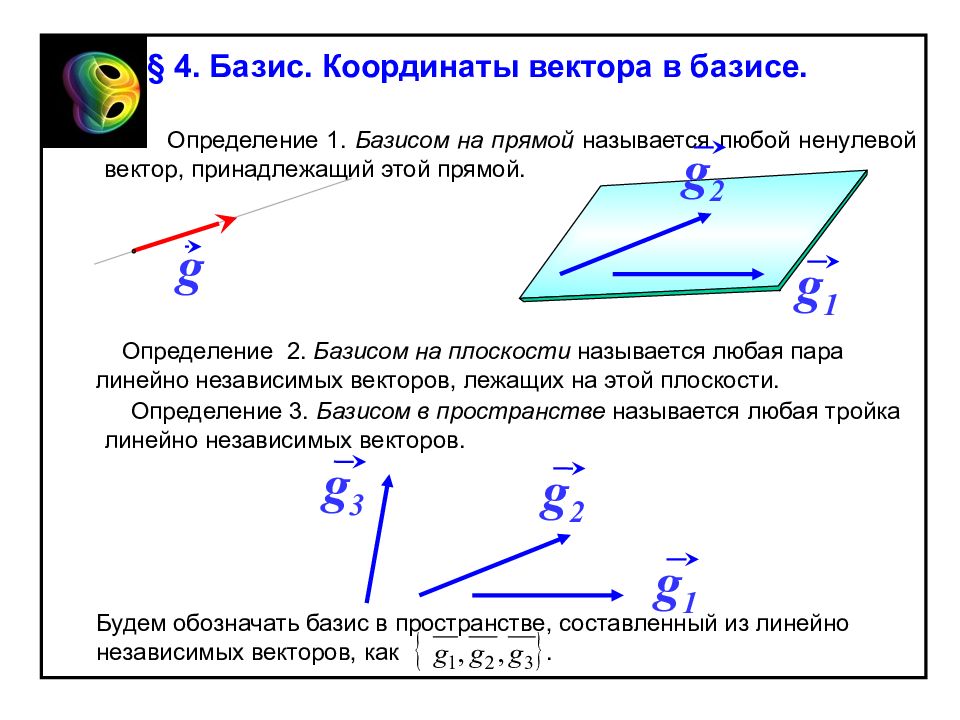
§ 4. Базис. Координаты вектора в базисе. Определение 1. Базисом на прямой называется любой ненулевой вектор, принадлежащий этой прямой. Определение 2. Базисом на плоскости называется любая пара линейно независимых векторов, лежащих на этой плоскости. Определение 3. Базисом в пространстве называется любая тройка линейно независимых векторов. g g 1 g 2 g 1 g 2 g 3 Будем обозначать базис в пространстве, составленный из линейно независимых векторов, как.
Слайд 33
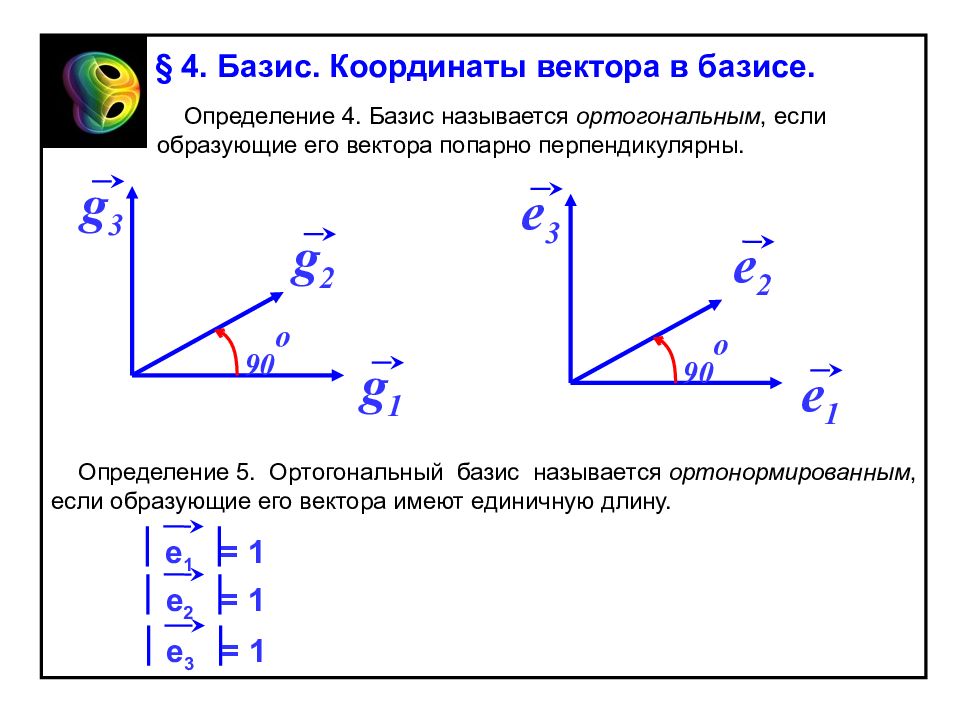
§ 4. Базис. Координаты вектора в базисе. Определение 4. Базис называется ортогональным, если образующие его вектора попарно перпендикулярны. Определение 5. Ортогональный базис называется ортонормированным, если образующие его вектора имеют единичную длину. g 1 g 2 g 3 90 o e 1 e 2 e 3 90 o e 1 = 1 e 2 = 1 e 3 = 1
Слайд 34
§ 4. Базис. Координаты вектора в базисе. Теорема 1. Любой вектор в пространстве с базисом может быть представлен, и причем единственным способом, в виде где α, β, γ – некоторые числа. Доказательство. Докажем вначале, что такие числа существуют. и в силу коллинеарности и в силу коллинеарности Следовательно, и Докажем единственность разложения по данному базису. Но это условие и означает, что вектора являются линейно зависимыми и не могут образовывать базис. Это, в свою очередь, доказывает единственность разложения. Пусть
Слайд 35
§ 4. Базис. Координаты вектора в базисе. Определение 6. Числа в разложении называются координатами вектора в базисе. Координаты – величины скалярные. Для краткой записи вектора в координатном представлении будем использовать следующую форму: т. е. каждому вектору в данном базисе можно поставить во взаимно однозначное соответствие матрицу-строку.
Слайд 36
§ 5. Действия с векторами в координатном представлении. В каждом конкретном базисе каждый вектор находится во взаимно-однозначном соответствии с упорядоченной тройкой чисел – своими координатами. Возникает вопрос о том, как выполнять операции с векторами в координатном представлении. С другой стороны, ранее были изучены матрицы и операции над ними, и целесообразно было бы свести операции с векторами в координатном представлении к матричным операциям. Теорема 1. Два вектора и равны тогда и только тогда, когда равны матрицы координат
Слайд 37
Теорема 2. Пусть в некотором базисе даны два вектора и Тогда в этом базисе Иными словами: при умножении вектора на число его координаты умножаются на это число; при сложении векторов складываются их соответствующие координаты. § 5. Действия с векторами в координатном представлении.
Слайд 38
Теорема 3. Два вектора и на плоскости линейно зависимы тогда и только тогда, когда их соответствующие координаты в некотором базисе пропорциональны, т. е. Доказательство. Необходимость. Пусть вектора и линейно зависимы, тогда по теореме 3.1 или в координатной форме Исключив λ из этих уравнений, получаем что и означает равенство нулю определителя. Достаточность. Пусть Тогда откуда Таким образом, вектора и пропорциональны, а, значит, и линейно зависимы. § 5. Действия с векторами в координатном представлении.
Слайд 39
Теорема 4. Три вектора в пространстве линейно зависимы тогда и только тогда, когда и Следствие. Равенства и соответственно являются необходимыми и достаточными условиями коллинеарности пары векторов на плоскости и компланарности тройки векторов в пространстве. § 5. Действия с векторами в координатном представлении.
Слайд 40
Пример 1. Показать, что вектора образуют базис в трехмерном пространстве. Решение. Вычислим определитель, столбцы которого представляют координаты векторов: Так как определитель отличен от нуля, то столбцы линейно независимы, т. е. указанные вектора образуют базис. § 5. Действия с векторами в координатном представлении.
Слайд 41
Пример 2. Разложить вектор по базису где Решение. Разложим вектор по базису с неопределенными коэффициентами В координатах это разложение представляет собой систему трех уравнений относительно Имеем: откуда по правилу Крамера Ответ: § 5. Действия с векторами в координатном представлении.
Слайд 42
§ 6. Декартова система координат. Определение 1. Совокупность базиса и точки О, в которую помещены начала всех базисных векторов, называется декартовой системой координат и обозначается Определение 2. Система координат состоящая из ортонормированного ортогонального базиса и точки О, называется прямоугольной декартовой системой координат. i j k x y z O Ох – ось абсцисс Оу – ось ординат О z – ось аппликат
Слайд 43
§ 6. Декартова система координат. Рене́ Дека́рт 1596 — 1650, — французский математик,, создатель аналитической геометрии и современной алгебраической символики, Декарт ввел математическую символику, близкую к современной. Коэффициенты он обозначал a, b, c …, а неизвестные — x, y, z. Натуральный показатель степени принял современный вид. Появилась черта над подкоренным выражением. Родился в городе Лаэ (ныне г. Декарт).
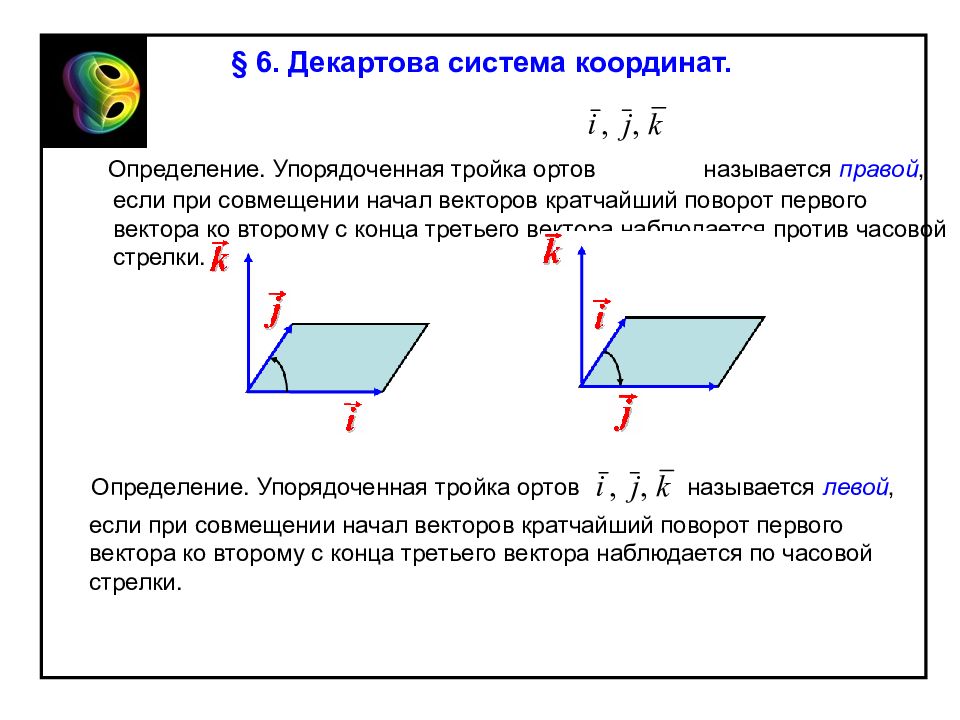
Слайд 44
§ 6. Декартова система координат. Определение. Упорядоченная тройка ортов называется правой, если при совмещении начал векторов кратчайший поворот первого вектора ко второму с конца третьего вектора наблюдается против часовой стрелки. Определение. Упорядоченная тройка ортов называется левой, если при совмещении начал векторов кратчайший поворот первого вектора ко второму с конца третьего вектора наблюдается по часовой стрелки.
Слайд 45
§ 6. Декартова система координат. Если задана система координат то произвольной точке М в пространстве можно поставить во взаимно однозначное соответствие вектор начало которого находится в точке О, а конец в точке М. Определение 3. Вектор называется радиус-вектором точки М в системе координат Определение 4. Координаты радиус-вектора точки М называются координатами точки М в системе координат
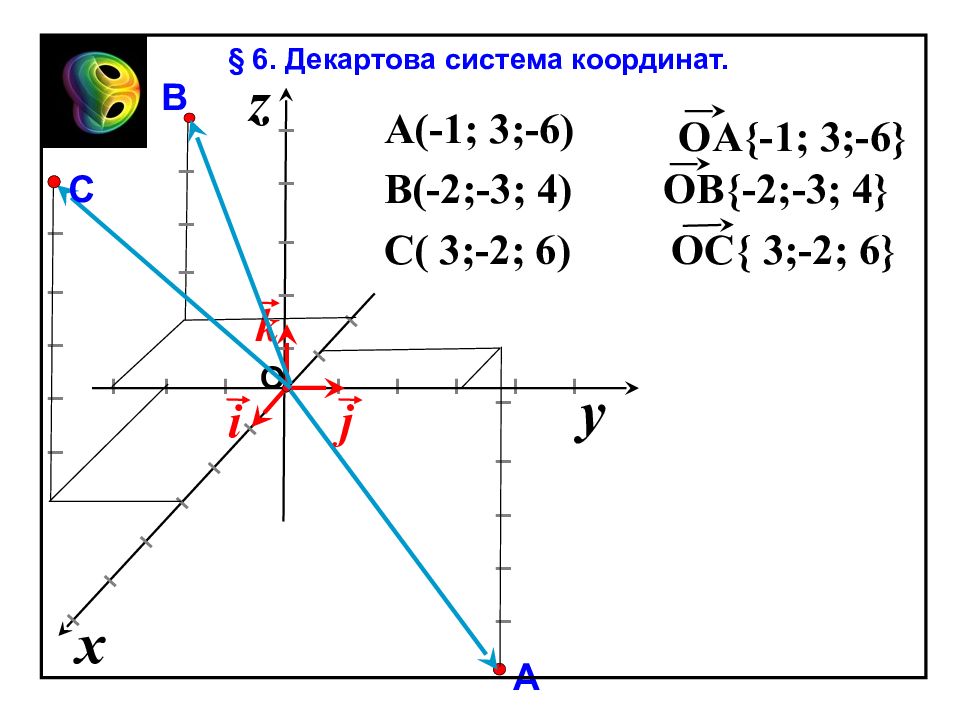
Слайд 46
A (-1 ; 3 ; -6 ) B( - 2;-3; 4) y x z I I I I I I I I I I I I I I I I I I I I I j k i O I I I В А I I I I I I I I I I С OB{ - 2;-3; 4} C( 3;-2; 6) OA{ -1 ; 3 ; -6 } OC{ 3;-2; 6} § 6. Декартова система координат.
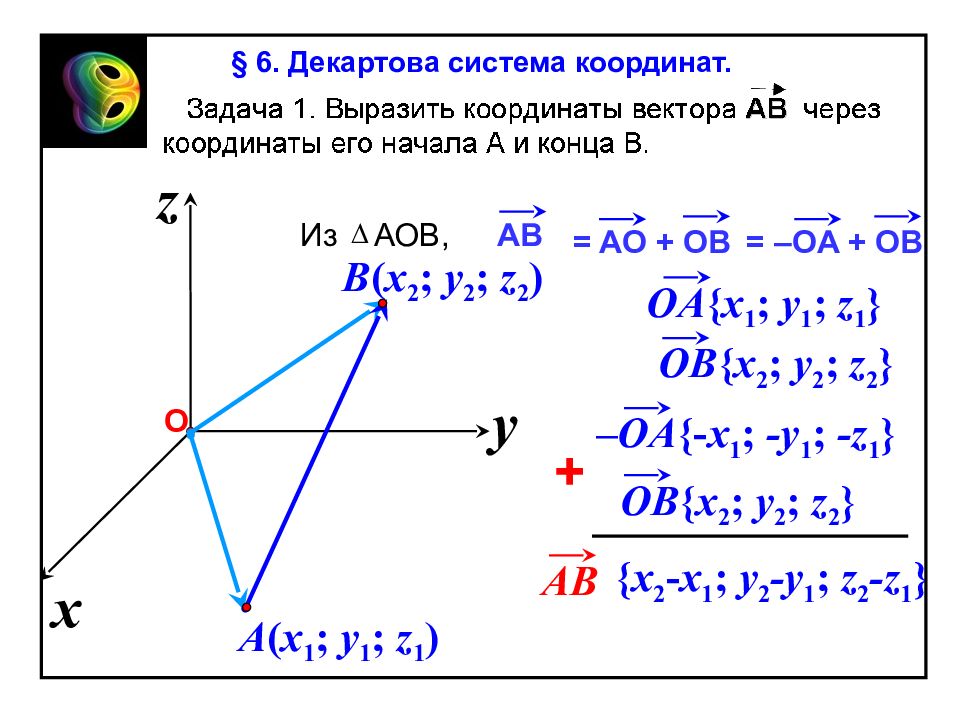
Слайд 47
x z y О A ( x 1 ; y 1 ; z 1 ) B ( x 2 ; y 2 ; z 2 ) Из АО B, = A О + О B AB = –О A + О B –OA {- x 1 ; -y 1 ; -z 1 } OB { x 2 ; y 2 ; z 2 } + AB { x 2 - x 1 ; y 2 -y 1 ; z 2 -z 1 } OA { x 1 ; y 1 ; z 1 } OB { x 2 ; y 2 ; z 2 } § 6. Декартова система координат.
Слайд 48
§ 6. Декартова система координат. Задача 2 (условие коллинеарности двух векторов в координатной форме). Пусть два вектора и коллинеарны. т. е. откуда или – условие коллинеарности двух векторов. Если два вектора коллинеарны, то их координаты пропорциональны. Тогда по теореме 3.1 существует такое число λ, при котором
Слайд 49
Пример 1. Коллинеарны ли вектора a { 2 ; 6 ; -3 }; 6 6 18 -9 b { 6 ; 18 ; -9 } 1 3 = = = Векторы и коллинеарны. a b § 6. Декартова система координат. = 3 b b a или a = 1 3
Слайд 50
§ 6. Декартова система координат. Пример 2. В декартовой системе координат A (1,3,0), B (2,0,-1), C (3,-3,-2). Доказать, что точки A, B, C лежат на одной прямой. Решение Очевидно, точки A, B, C лежат на одной прямой, если векторы и коллинеарны. Для этого необходимо выполнение условия: . Отсюда следует (теорема 5.2), что координаты векторов и должны быть пропорциональны. Таким образом, точки A, B, C лежат на одной прямой.
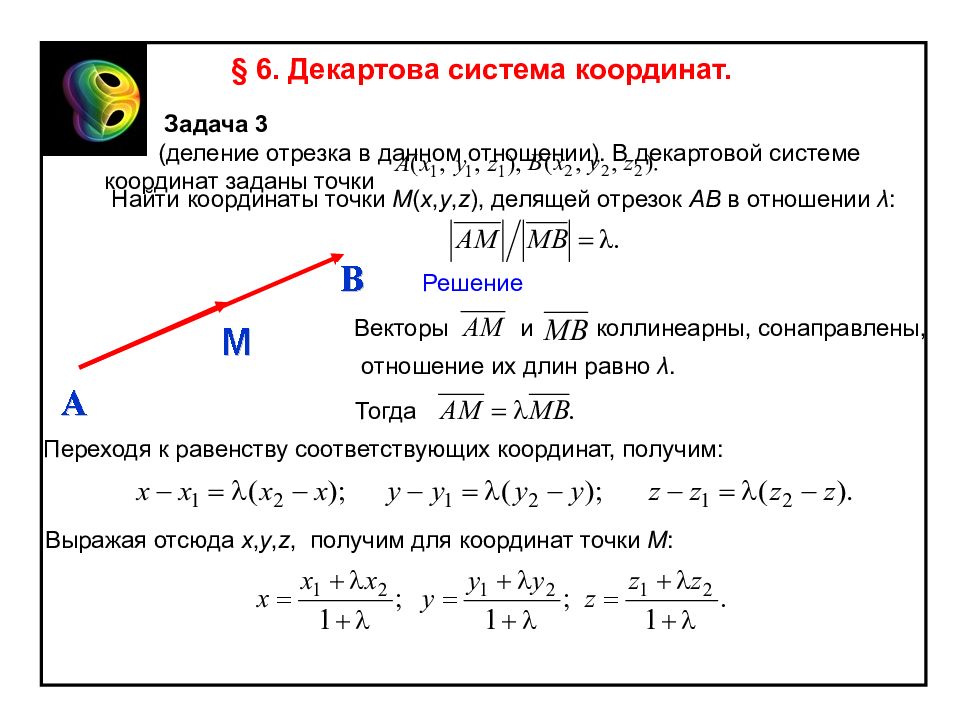
Слайд 51
§ 6. Декартова система координат. Задача 3 ( деление отрезка в данном отношении). В декартовой системе координат заданы точки Найти координаты точки M ( x, y, z ), делящей отрезок AB в отношении λ : Векторы Решение и коллинеарны, сонаправлены, отношение их длин равно λ. Тогда Переходя к равенству соответствующих координат, получим: Выражая отсюда x, y, z, получим для координат точки M :
Слайд 52
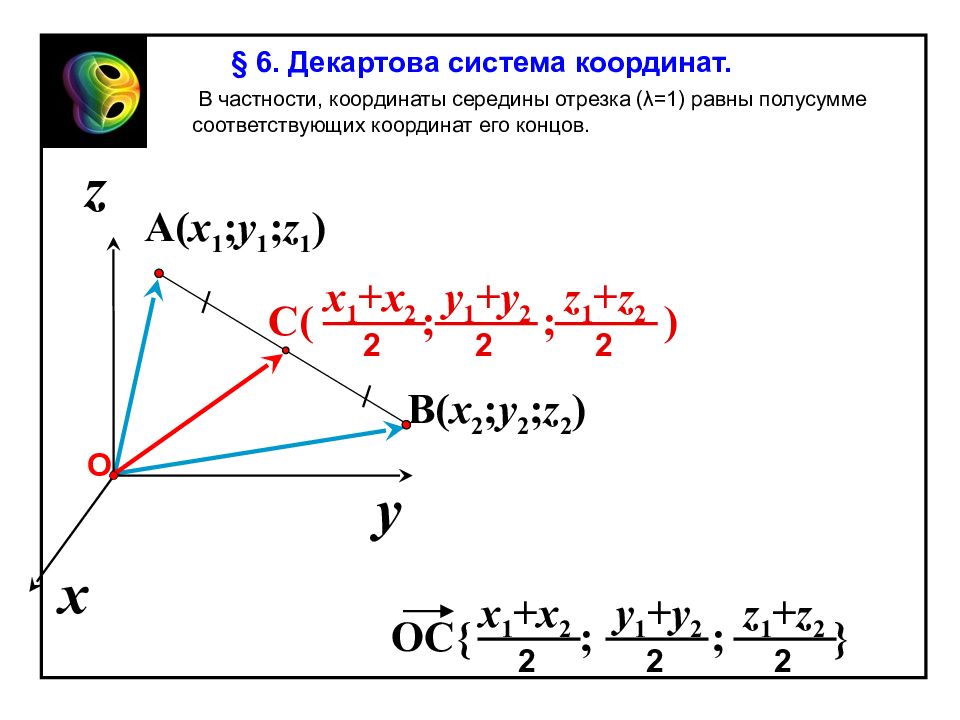
A ( x 1 ; y 1 ; z 1 ) x z y О B ( x 2 ; y 2 ; z 2 ) В частности, координаты середины отрезка (λ=1) равны полусумме соответствующих координат его концов. C ( ; ; ) y 1 + y 2 2 x 1 + x 2 2 z 1 + z 2 2 { ; ; } y 1 + y 2 2 x 1 + x 2 2 z 1 + z 2 2 OC § 6. Декартова система координат.
Слайд 53
§ 6. Декартова система координат. Пример. Разделить отрезок АВ ( А (3,5; 1), B (2; 2)) на три равные части. Решение
Слайд 54
§ 7. Проекция вектора на ось. Пусть вектор лежит на некоторой оси l. Направление орта соответствует направлению оси. l Определение 1. Проекцией вектора, лежащего на оси, на эту ось называется число, по абсолютной величине равное длине вектора и взятое со знаком плюс, если направление вектора совпадает с направлением оси и со знаком минус, если они противоположны. Пусть вектор не лежит на некоторой оси l. Из точек А и B опустим перпендикуляры на ось. Вектор называется компонентой вектора по оси l. Определение 2. Проекцией вектора, не лежащего на оси l, на эту ось называется проекция его компоненты по оси l на эту же ось. Проекция вектора на ось обычно обозначается так:
Слайд 55
§ 7. Проекция вектора на ось. Свойства проекций вектора на ось: 1. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью: где θ – угол между вектором и осью. 2. Проекция суммы векторов на ось равна сумме проекций этих векторов на эту же ось, т. е. . 3. Проекция на ось вектора, умноженного на число, равна произведению проекции вектора на это число, т. е. 4. Проекции на ось двух равных векторов равны между собой.
Слайд 56
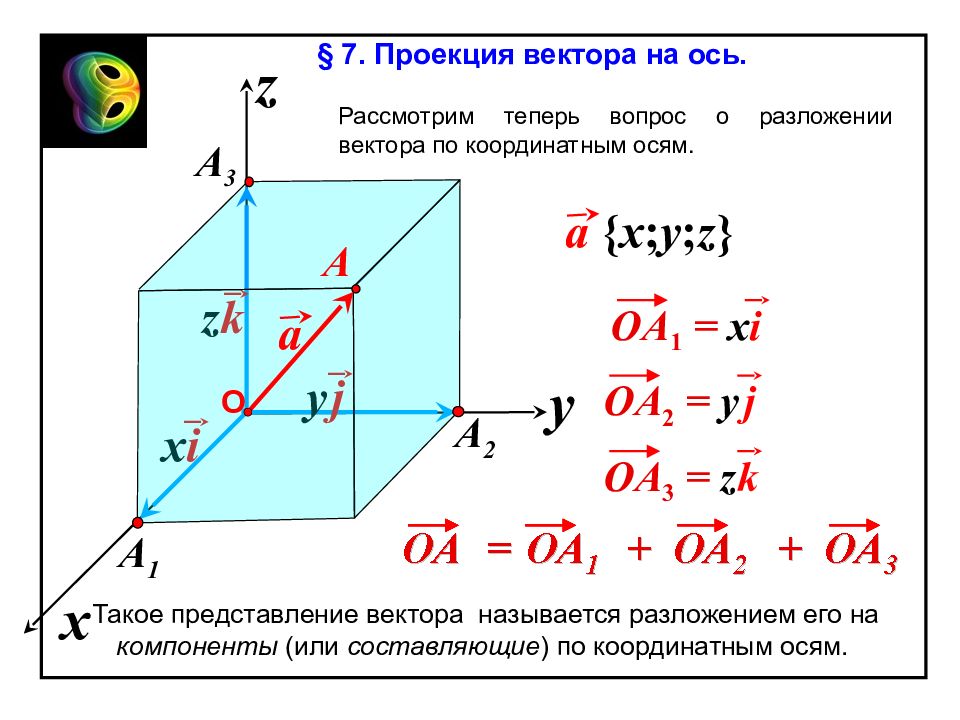
z k y j x i A 1 OA 3 = z k OA 1 = x i x z y A 2 a a { x ; y ; z } OA 2 = y j О A A 3 § 7. Проекция вектора на ось. Рассмотрим теперь вопрос о разложении вектора по координатным осям. Такое представление вектора называется разложением его на компоненты (или составляющие ) по координатным осям.
Слайд 57
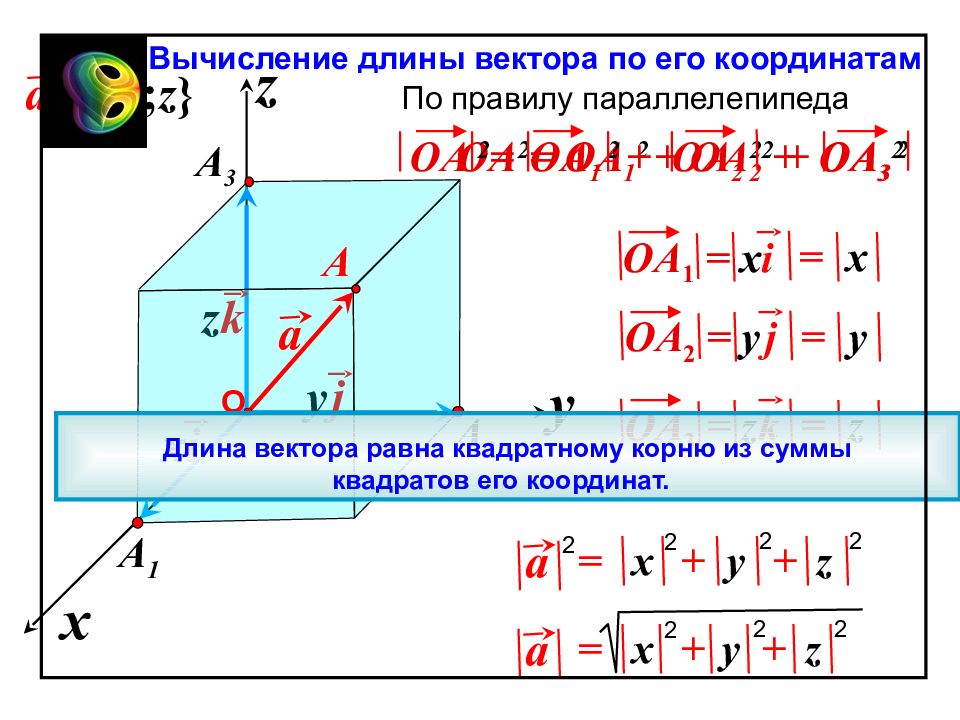
z k y j x i + + y z x = a 2 2 2 A 1 OA 3 = z k OA 1 = x i x z y A 2 Вычисление длины вектора по его координатам OA 2 = OA 1 2 + OA 2 2 + OA 3 2 По правилу параллелепипеда OA 2 = OA 1 2 + OA 2 2 + OA 3 2 a a { x ; y ; z } = x OA 2 = y j = = z y y = a x + + z 2 2 2 2 О A A 3 Длина вектора равна квадратному корню из суммы квадратов его координат.
Слайд 58
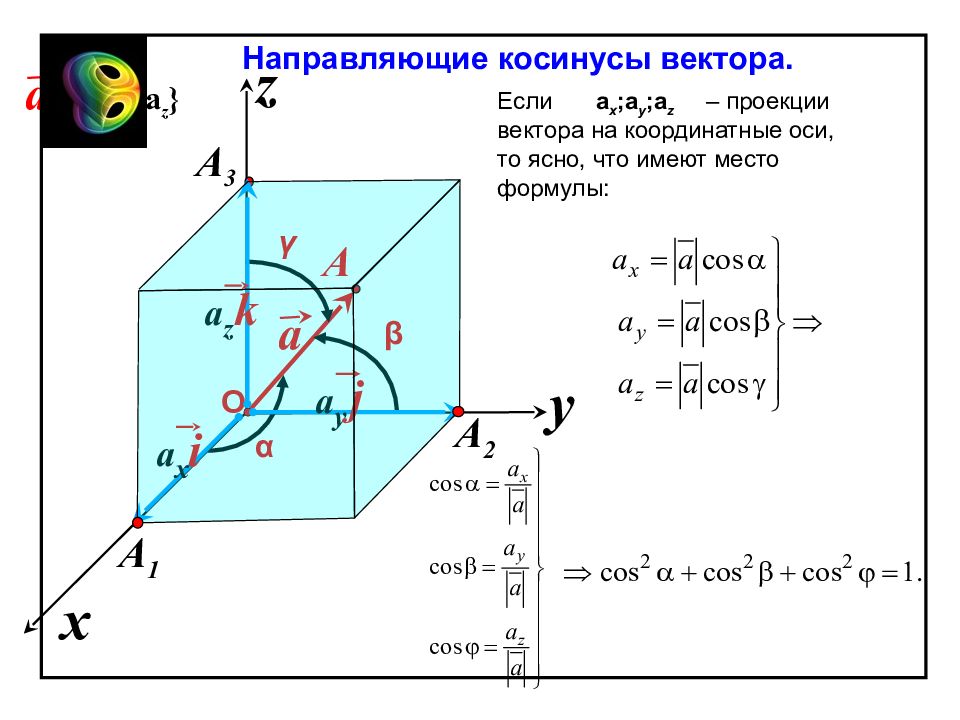
x z y Направляющие косинусы вектора. a a { а x ; а y ; а z } О A A 3 α β γ Если – проекции вектора на координатные оси, то ясно, что имеют место формулы: а x i а y j а z k A 2 A 1 а x ; а y ; а z
Слайд 59
§ 7. Проекция вектора на ось. Пример 1. Даны точки A (1, –1, 2) и B (3, 2, 3). Найти: Найти: Найти: Найти: Найти: Координаты вектора Длину вектора Так как значит Направляющие косинусы вектора Разложение вектора по базису; Так как значит Единичный вектор (орт), соответствующий вектору Так как значит
Слайд 60
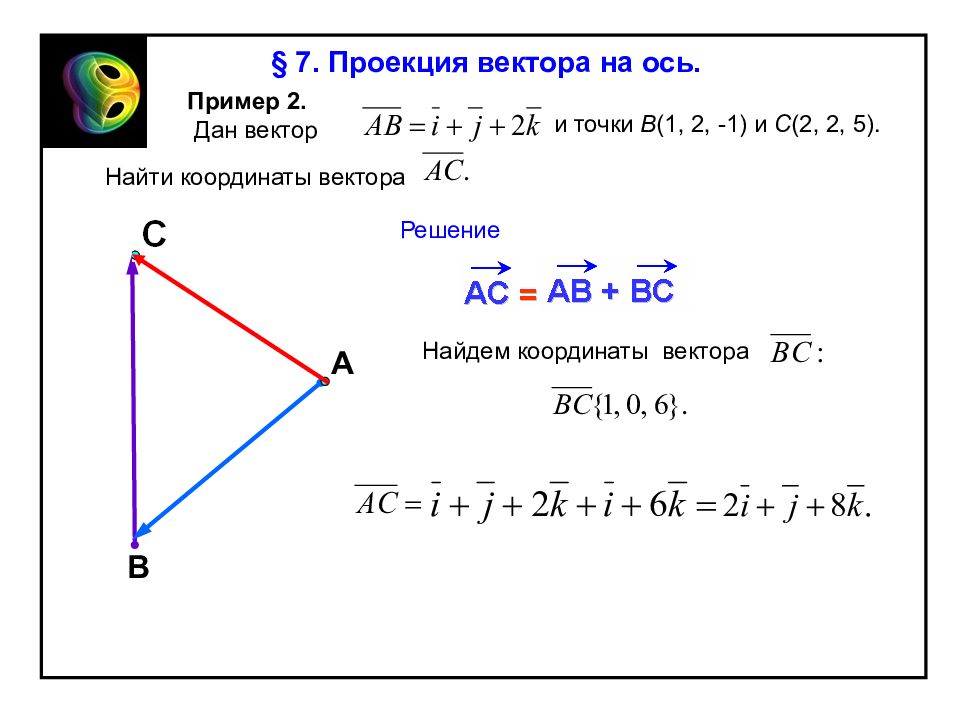
В А § 7. Проекция вектора на ось. Пример 2. Дан вектор и точки В (1, 2, -1) и С (2, 2, 5). Найти координаты вектора Решение Найдем координаты вектора
Слайд 61
§ 7. Проекция вектора на ось. Пример 3. Выяснить, при каких значениях параметров вектора Решение Два вектора коллинеарны, если существует некая константа c такая, что имеет место соотношение Отсюда следует, что откуда Так как орты линейно независимы, ибо они представляют собою базис, то должны обращаться в нуль коэффициенты этой линейной комбинации, т. е. откуда и коллинеарны.
Слайд 62
Скалярным произведением двух ненулевых векторов называется произведение их длин на косинус угла между ними. a b = a b cos ( ) a b § 8. Скалярное произведение векторов. Если хотя бы один из векторов равен нулю, то скалярное произведение этих векторов равно нулю (по определению). Скалярное произведение векторов – число (скаляр). Скаляр – лат. scale – лестница, шкала. Ввел в 1845г. У. Гамильтон, ирландский математик.
Слайд 63
a b = a b cos 90 0 a b = 0 0 Если векторы и перпендикулярны, то скалярное произведение векторов равно нулю. a b Обратно: если, то векторы и перпендикулярны. a b = 0 a b a b = 0 a b ^ Û Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. a b = 90 0 § 8. Скалярное произведение векторов.
Слайд 64
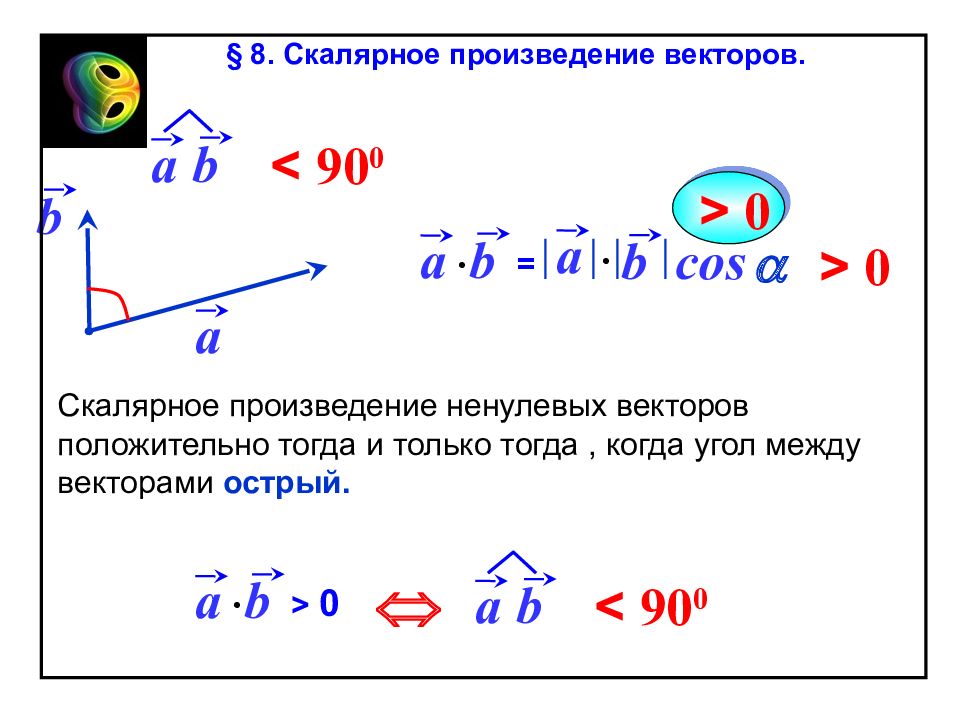
a b = a b cos a b Скалярное произведение ненулевых векторов положительно тогда и только тогда, когда угол между векторами острый. a b > 0 Û a > 0 > 0 a b < 90 0 a b < 90 0 § 8. Скалярное произведение векторов.
Слайд 65
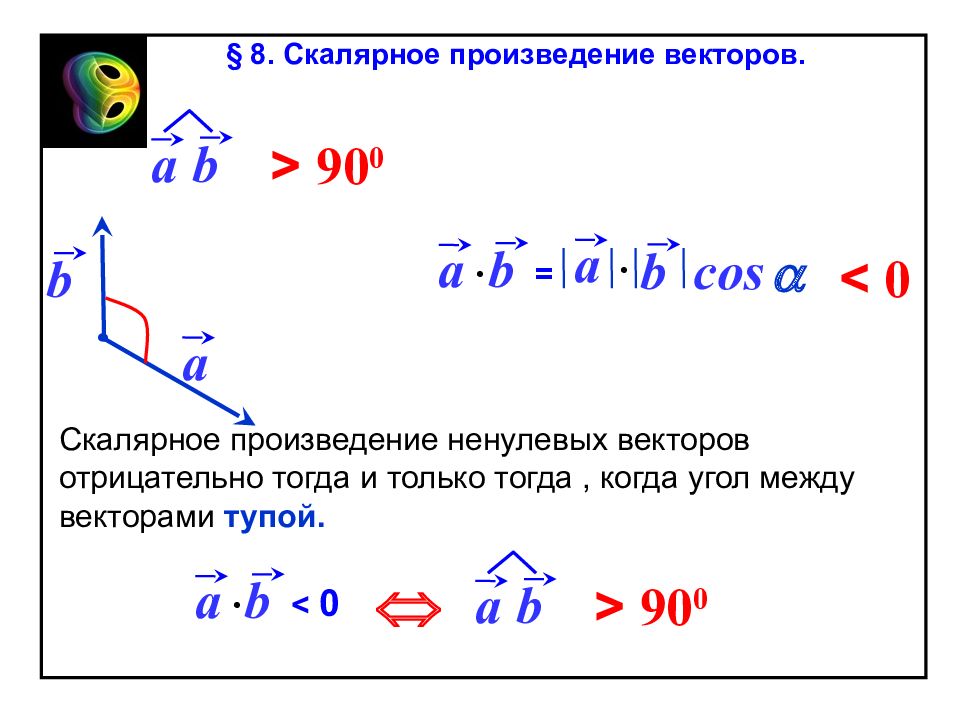
a b = a b cos a b Скалярное произведение ненулевых векторов отрицательно тогда и только тогда, когда угол между векторами тупой. a b < 0 Û a < 0 a b > 90 0 a b > 90 0 § 8. Скалярное произведение векторов.
Слайд 66
a b = a b = a b cos 0 0 a b a b = 0 0 Если a b a b = a b cos 180 0 a b a b = 180 0 Если a b = – a b § 8. Скалярное произведение векторов.
Слайд 67
a a = a a cos a 0 0 a a = 0 0 a a = = a 2 Скалярное произведение называется скалярным квадратом вектора и обозначается a a a a 2 Таким образом, a 2 = a 2 § 8. Скалярное произведение векторов. откуда Длина вектора равен квадратному корню из его скалярного квадрата.
Слайд 68
§ 8. Скалярное произведение векторов. Свойства скалярного произведения: Действительно, Отсюда следует формула для нахождения проекции одного вектора на другой: тогда 2) Переместительное или коммутативное свойство: 3) Сочетательное (ассоциативное) свойство: 4) Распределительное (дистрибутивное) свойство относительного сложения векторов:
Слайд 69
§ 8. Скалярное произведение векторов. . Выведем формулу скалярного произведения в координатной форме. a { а x ; а y ; а z } b {b x ;b y ;b z } т.к. В частности,
Слайд 70
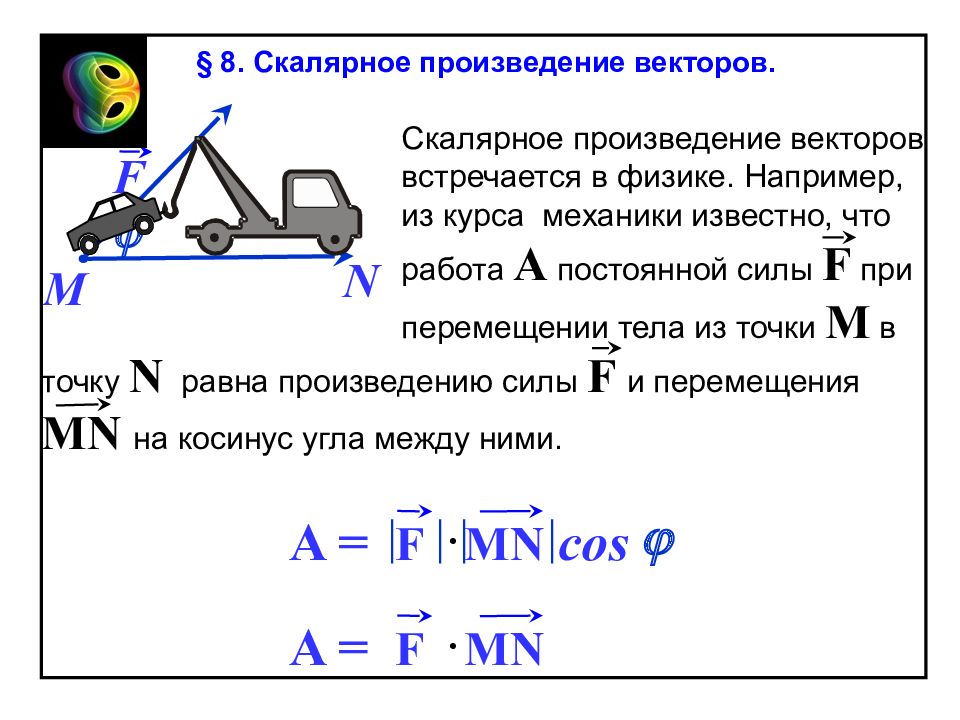
A = F MN cos j F j N M A = F MN точку N равна произведению силы F и перемещения MN на косинус угла между ними. Скалярное произведение векторов встречается в физике. Например, из курса механики известно, что работа A постоянной силы F при перемещении тела из точки M в § 8. Скалярное произведение векторов.
Слайд 71
§ 8. Скалярное произведение векторов. Скалярное произведение двух векторов позволяет решить следующие задачи векторной алгебры: Нахождение угла между двумя векторами. Отсюда нетрудно получить условие ортогональности (перпендикулярности) двух векторов в координатной форме:
Слайд 72
§ 8. Скалярное произведение векторов. Пример 1. Даны вершины треугольника: A (2; –1; 3), B (1; 1; 1), C (0; 0; 5). Найти Решение
Слайд 73
§ 8. Скалярное произведение векторов. 2. Нахождение проекции одного вектора на направление другого Пример 2. Даны три точки A (2; 3; 5), B (1; 2; 2), C (3; 5; 4). Найти Решение
Слайд 74
§ 8. Скалярное произведение векторов. 3. Нахождение длины вектора. Пример 3. Дан вектор Найти длину вектора Решение Найдем скалярный квадрат вектора
Слайд 75
§ 8. Скалярное произведение векторов. Определить длины диагоналей параллелограмма, построенного на векторах и где угол между которыми равен 60°. – единичные векторы, Решение
Слайд 76
§ 8. Скалярное произведение векторов. 4) Доказательство ортогональности векторов Пример 5. При каком значении α ортогональны вектора и Решение Принимая во внимание условие ортогональности двух векторов получим 5) Задачи с механическим содержанием Пример 6. Даны три постоянные силы приложенные в одной точке. Найти работу равнодействующей этих сил на прямолинейном перемещении из положения М 1 (4,4,6) в положение М 2 (7,5,2). Равнодействующая сила Вектор перемещения Искомая работа Решение
Слайд 77
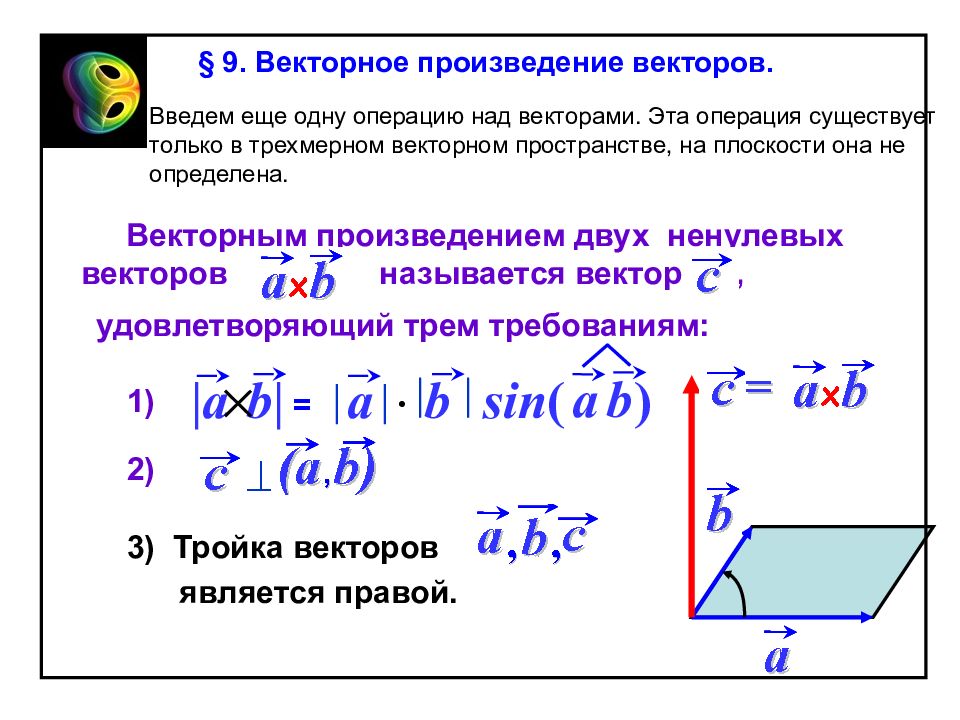
Векторным произведением двух ненулевых векторов называется вектор, § 9. Векторное произведение векторов. Введем еще одну операцию над векторами. Эта операция существует только в трехмерном векторном пространстве, на плоскости она не определена. удовлетворяющий трем требованиям: | a b | = a b sin ( ) a b 1) 2) 3) Тройка векторов является правой.
Слайд 79
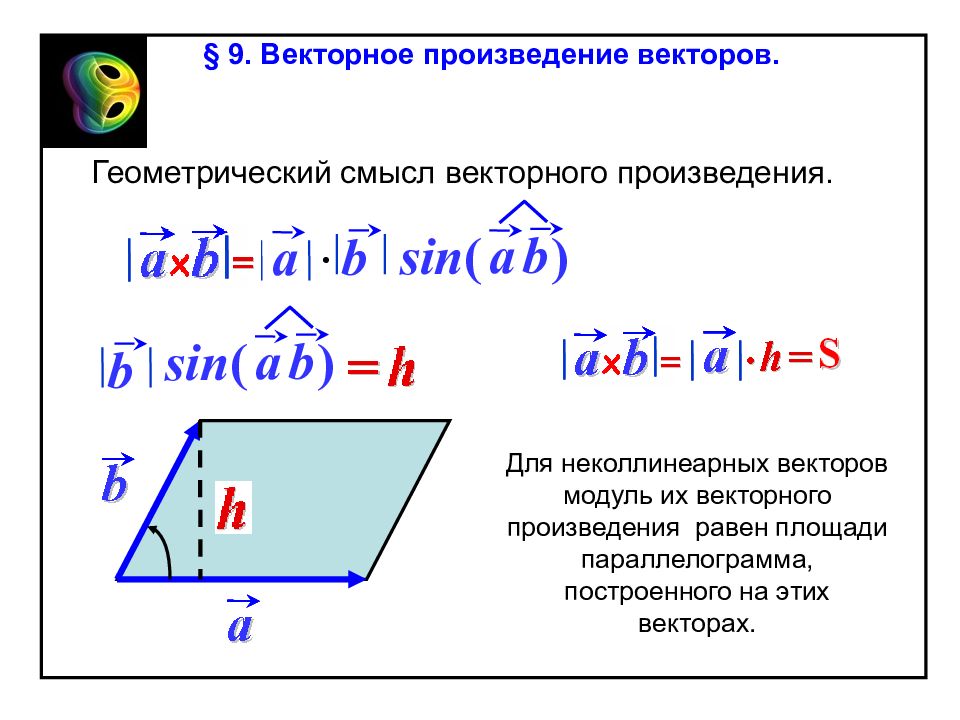
§ 9. Векторное произведение векторов. Геометрический смысл векторного произведения. a b sin ( ) a b sin ( ) a b b Для неколлинеарных векторов модуль их векторного произведения равен площади параллелограмма, построенного на этих векторах.
Слайд 80
§ 9. Векторное произведение векторов. Свойства векторного произведения: Свойство очевидно, так как синус – функция нечетная. 2 ) Свойство сочетательности относительно скалярного множителя: 3 ) Распределительное свойство относительно сложения векторов:
Слайд 81
a b sin b 0 0 a b = 0 0 § 8. Векторное произведение векторов. Признак коллинеарности векторов: Для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было бы равно нулю. a Если вектора коллинеарные, то В частности, имеем для ортов:
Слайд 82
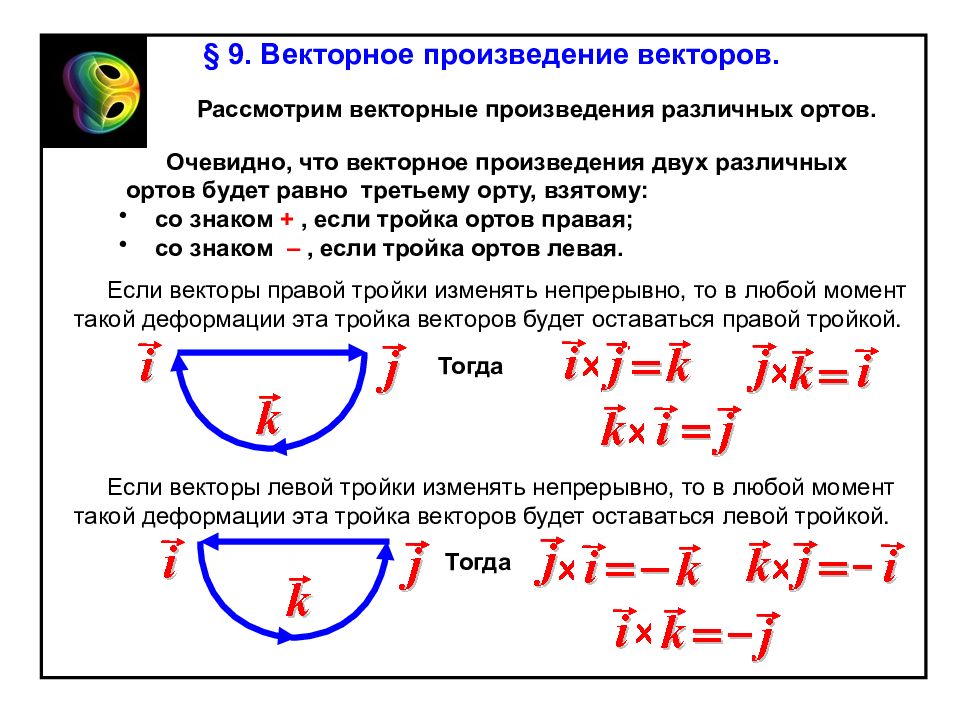
§ 9. Векторное произведение векторов. Рассмотрим векторные произведения различных ортов. Очевидно, что векторное произведения двух различных ортов будет равно третьему орту, взятому: со знаком +, если тройка ортов правая; со знаком –, если тройка ортов левая. Тогда Если векторы правой тройки изменять непрерывно, то в любой момент такой деформации эта тройка векторов будет оставаться правой тройкой. Если векторы левой тройки изменять непрерывно, то в любой момент такой деформации эта тройка векторов будет оставаться левой тройкой. Тогда
Слайд 83
§ 9. Векторное произведение векторов. Выразим теперь векторное произведение через координаты векторов, его составляющих.
Слайд 84
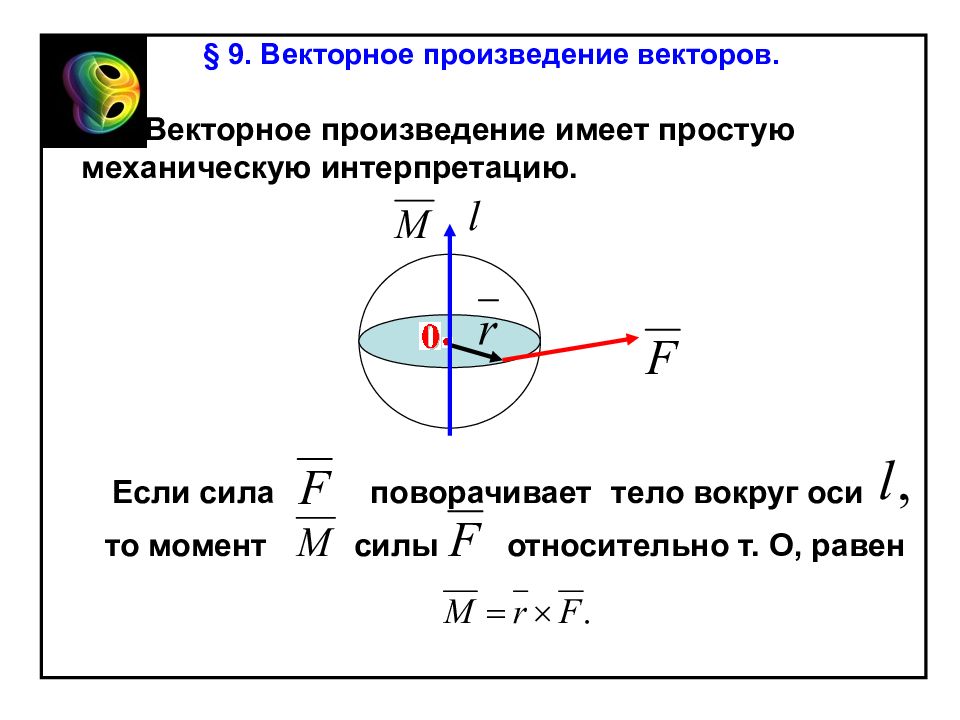
§ 9. Векторное произведение векторов. Векторное произведение имеет простую механическую интерпретацию. Если сила поворачивает тело вокруг оси то момент силы относительно т. О, равен
Слайд 85
§ 9. Векторное произведение векторов. Векторное произведение двух векторов позволяет решить следующие задачи векторной алгебры. 1) Нахождение площади параллелограмма и треугольника
Слайд 86
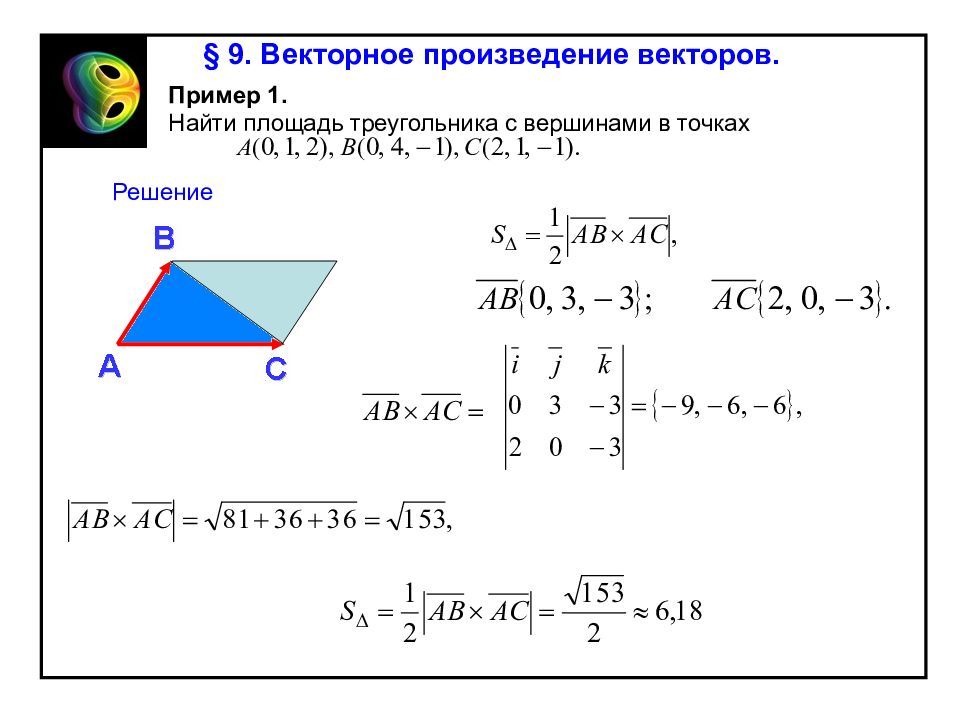
§ 9. Векторное произведение векторов. Пример 1. Найти площадь треугольника с вершинами в точках Решение
Слайд 87
§ 9. Векторное произведение векторов. Пример 2. Найти площадь треугольника, построенного на векторах Решение
Слайд 88
§ 9. Векторное произведение векторов. 2) Нахождение векторов, перпендикулярных данной плоскости Пример 3. Найти единичный вектор, перпендикулярный к плоскости, в которой лежат точки Решение В силу определения векторного произведения векторов Поставленной задаче удовлетворяют два единичных вектора
Слайд 89
§ 9. Векторное произведение векторов. 3) Доказательство коллинеарности векторов Решение Условие коллинеарности: т. е. вектора неколлинеарны. 4) Задачи механического содержания Решение
Слайд 90
§ 10. Смешанное произведение векторов. Определение 1. Смешанным произведением ненулевых векторов называется скалярное произведение вектора и векторного произведения вектора на вектор, т. е. выражение Свойства смешанного произведения: 1) Смешанное произведение не меняется при циклической перестановке перемножаемых векторов. 2) При перестановке двух соседних векторов модуль смешанного произведения не меняется, а знак меняется на противоположный, т. к. тройка меняет свою ориентацию. т.е. порядок знаков умножения не важен. Поэтому принято смешанное произведение обозначать
Слайд 91
§ 10. Смешанное произведение векторов. Выразим теперь смешанное произведение через координаты векторов, его составляющих. или
Слайд 92
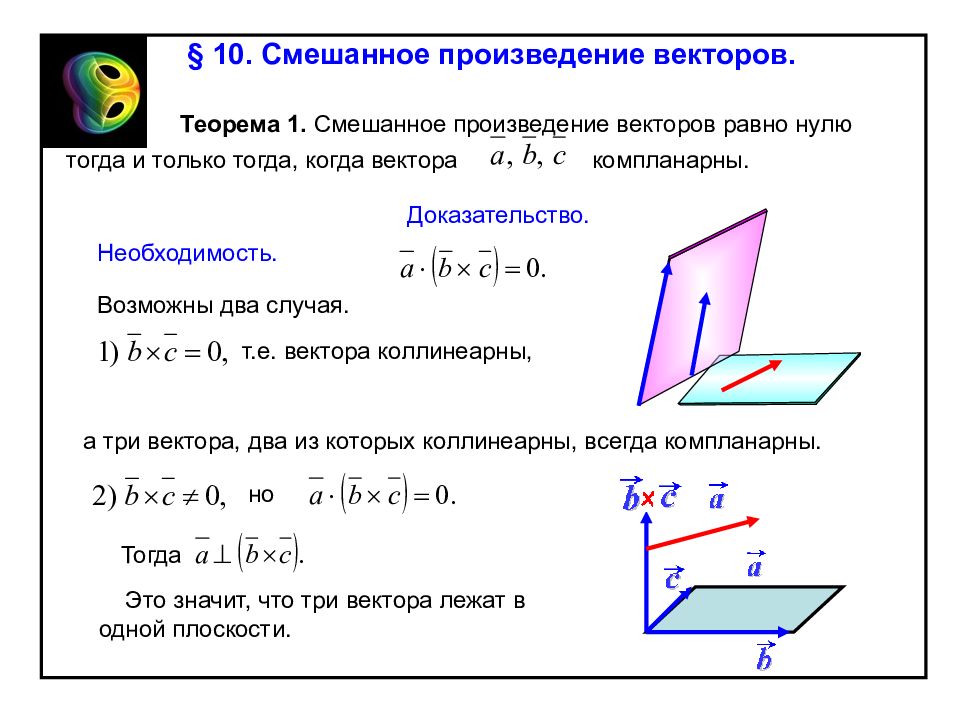
§ 10. Смешанное произведение векторов. Теорема 1. Смешанное произведение векторов равно нулю тогда и только тогда, когда вектора компланарны. Доказательство. Необходимость. Возможны два случая. т.е. вектора коллинеарны, а три вектора, два из которых коллинеарны, всегда компланарны. Тогда но Это значит, что три вектора лежат в одной плоскости.
Слайд 93
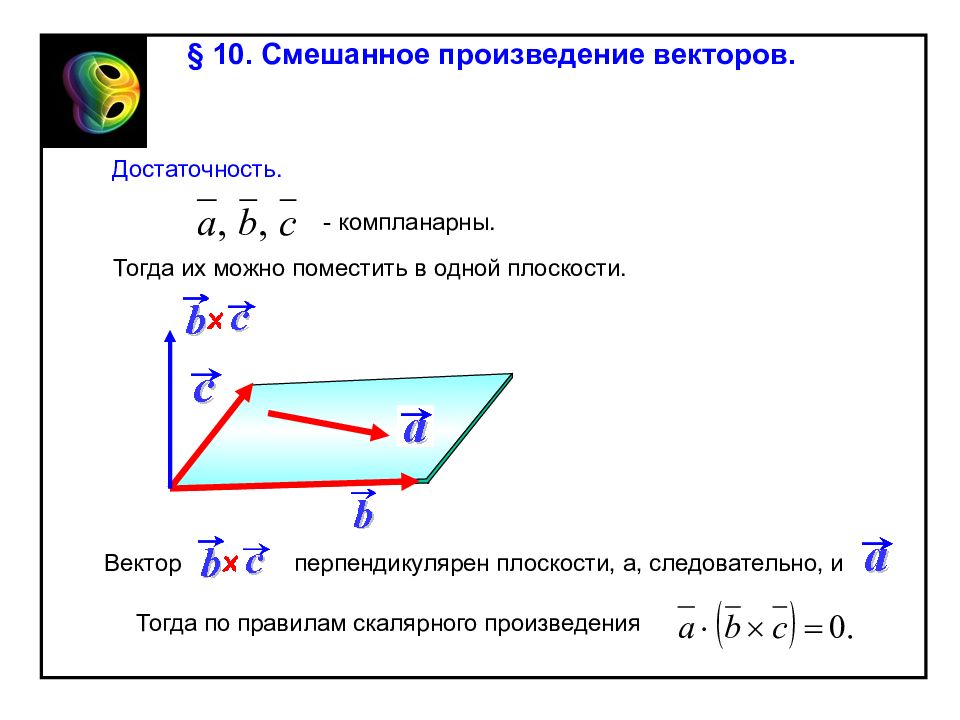
§ 10. Смешанное произведение векторов. Достаточность. - компланарны. Тогда их можно поместить в одной плоскости. Вектор перпендикулярен плоскости, а, следовательно, и Тогда по правилам скалярного произведения
Слайд 94
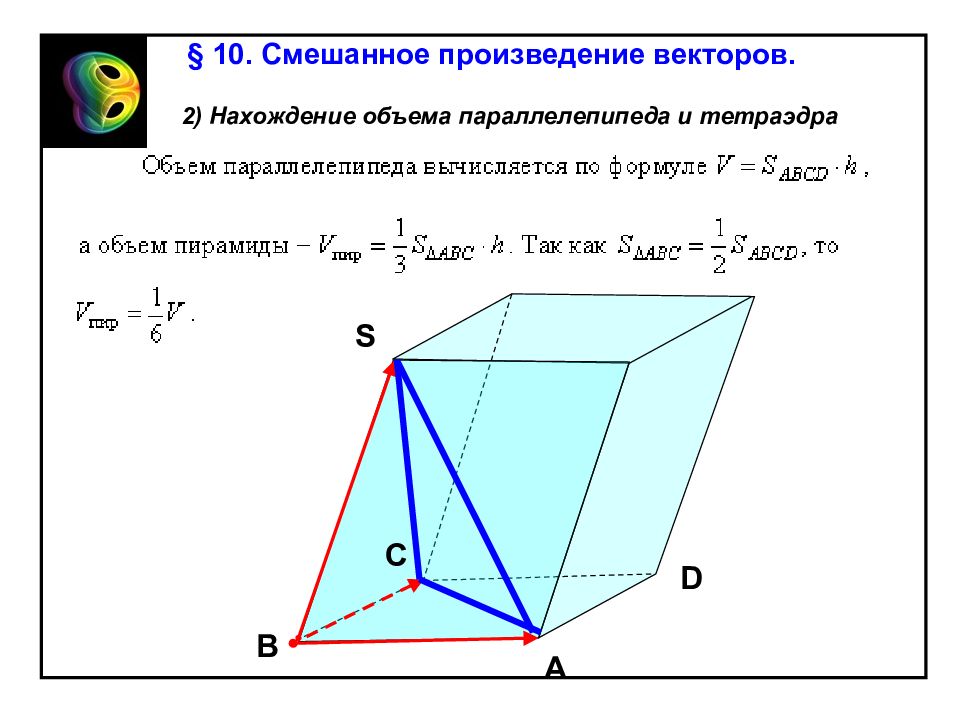
§ 10. Смешанное произведение векторов. Установим геометрический смысл смешанного произведения векторов. Теорема 2. Смешанное произведение некомпланарных векторов равно объему параллелепипеда, сторонами которого служат эти вектора, взятому со знаком +, если тройка векторов правая, и со знаком -, если тройка левая. Доказательство. В А D Но тогда
Слайд 95
§ 10. Смешанное произведение векторов. Смешанное произведение трех векторов позволяет решить c ледующие задачи векторной алгебры: 1) Доказательство компланарности (линейной зависимости) трех векторов Пример 1. Показать, что точки А (1, 2, 1), В (3, 3, 3), С (4, 1, 2) и D (5, 4, 5) лежат в одной плоскости. Решение А B C D Если точки А, В, С и D лежат в одной плоскости, то и вектора лежат в одной плоскости, а тогда смешанное произведение этих векторов равно нулю. Следовательно, точки лежат в одной плоскости.
Слайд 96
§ 10. Смешанное произведение векторов. Решение т. е. существуют константы λ, μ и ν такие, что Следовательно, векторы компланарны, а значит, они линейно зависимы, Данная система имеет бесчисленное множество решений. откуда получим искомую линейную зависимость:
Слайд 97
§ 10. Смешанное произведение векторов. 2) Нахождение объема параллелепипеда и тетраэдра В А D С S