Сечение поверхности плоскостью
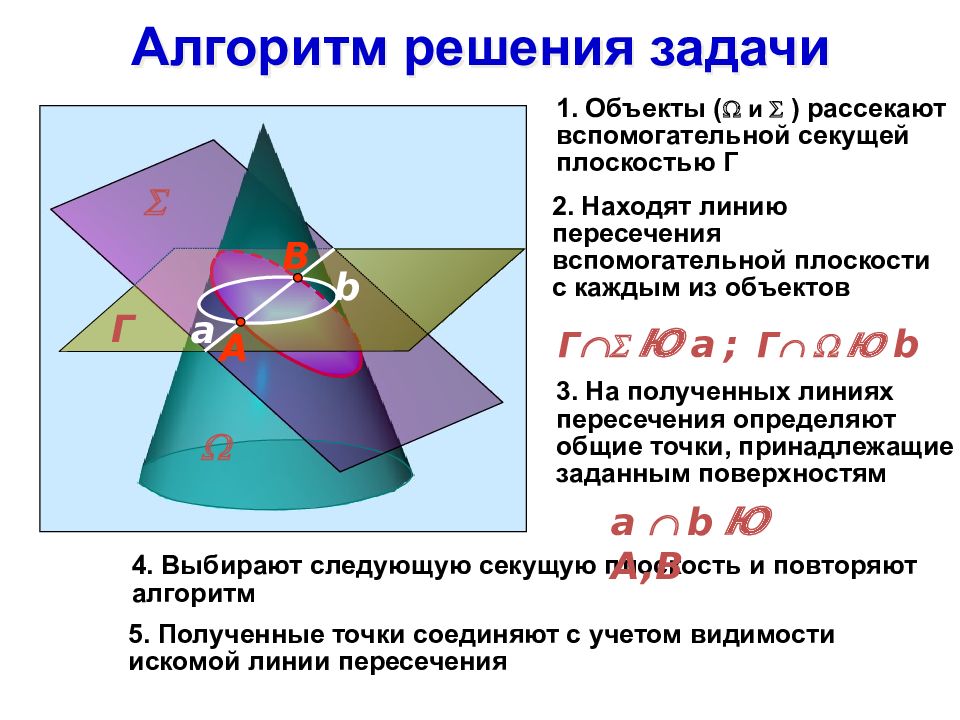
Алгоритм решения задачи 1. Объекты ( и ) рассекают вспомогательной секущей плоскостью Г 2. Находят линию пересечения вспомогательной плоскости с каждым из объектов 4. Выбирают следующую секущую плоскость и повторяют алгоритм 5. Полученные точки соединяют с учетом видимости искомой линии пересечения Г Ю b Г Ю а ; a b Ю A,B 3. На полученных линиях пересечения определяют общие точки, принадлежащие заданным поверхностям Г а b А B
Методические указания Плоскость, пересекающая поверхность, может занимать общее и частное положение относительно плоскостей проекций В общем случае вид сечения – кривая линия Сечение поверхности вращения плоскостью является фигурой симметричной. Ось симметрии фигуры сечения лежит в плоскости общей симметрии заданной поверхности и плоскости, при условии: - проходит через ось вращения поверхности; - перпендикулярности секущей плоскости Сечением многогранной поверхности является ломаная линия, вершины которой лежат на ребрах поверхности
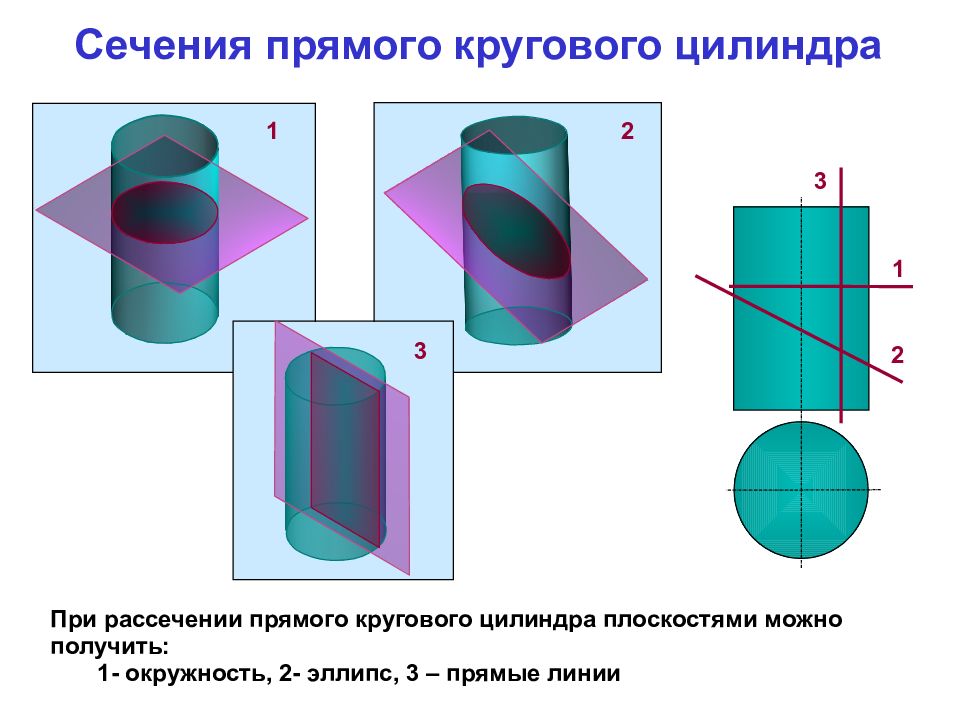
2 1 При рассечении прямого кругового цилиндра плоскостями можно получить: 1- окружность, 2- эллипс, 3 – прямые линии Сечения прямого кругового цилиндра 3 2 1 3
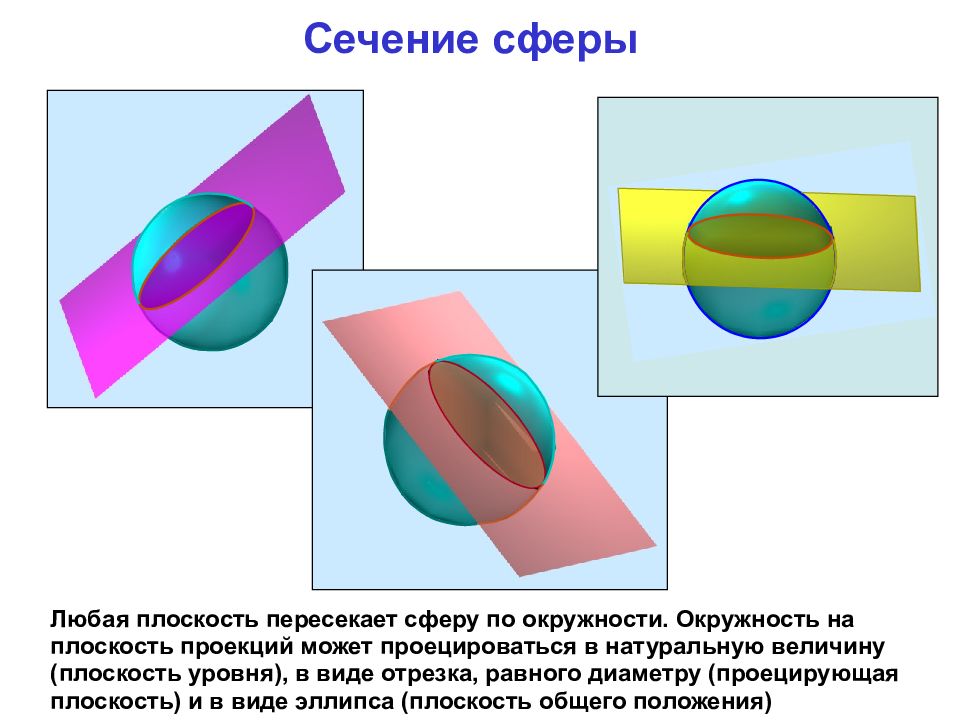
Сечение сферы Любая плоскость пересекает сферу по окружности. Окружность на плоскость проекций может проецироваться в натуральную величину (плоскость уровня), в виде отрезка, равного диаметру (проецирующая плоскость) и в виде эллипса (плоскость общего положения)
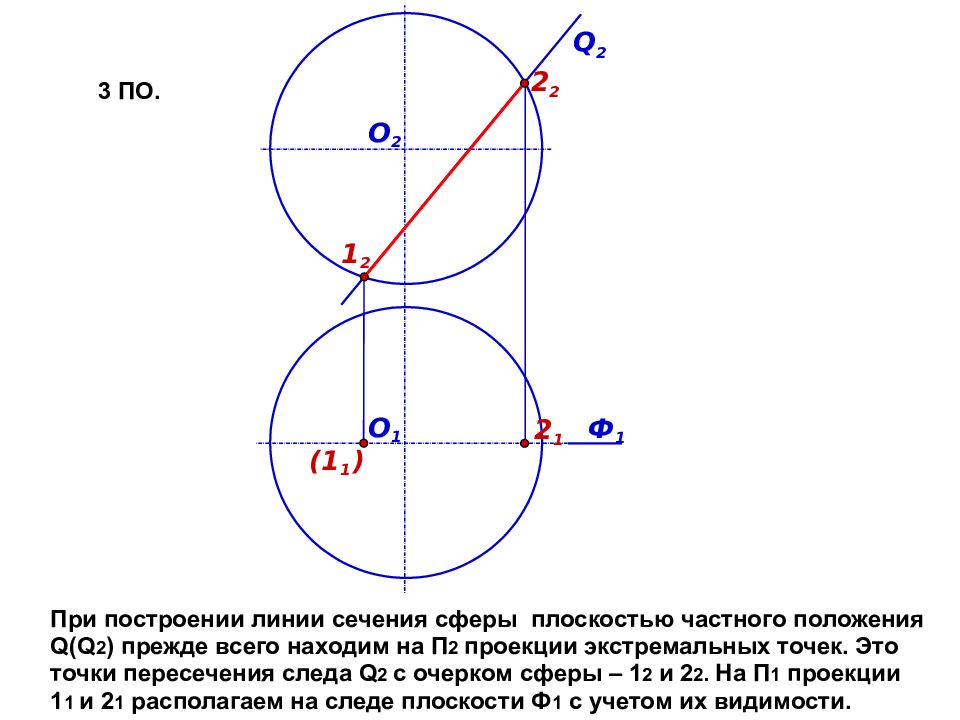
Ф 1 Q 2 О 1 О 2 (1 1 ) 1 2 2 1 2 2 При построении линии сечения сферы плоскостью частного положения Q(Q 2 ) прежде всего находим на П 2 проекции экстремальных точек. Это точки пересечения следа Q 2 с очерком сферы – 1 2 и 2 2. На П 1 проекции 1 1 и 2 1 располагаем на следе плоскости Ф 1 с учетом их видимости. 3 ПО.
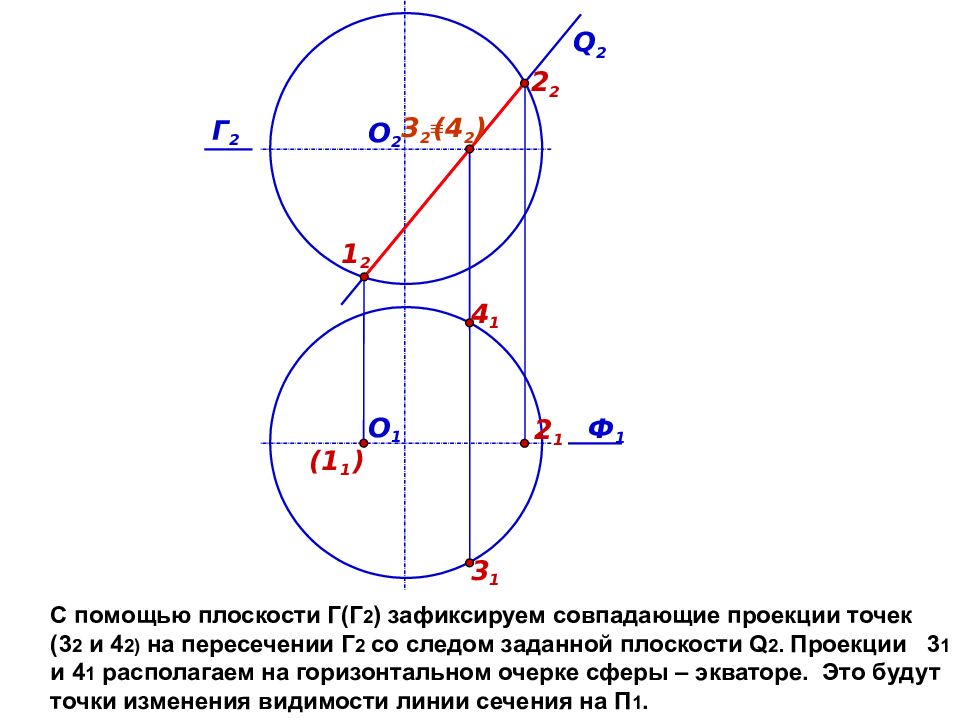
С помощью плоскости Г(Г 2 ) зафиксируем совпадающие проекции точек (3 2 и 4 2) на пересечении Г 2 со следом заданной плоскости Q 2. Проекции 3 1 и 4 1 располагаем на горизонтальном очерке сферы – экваторе. Это будут точки изменения видимости линии сечения на П 1. Ф 1 Q 2 О 1 О 2 3 1 ( 4 2 ) 3 2 Г 2 4 1 (1 1 ) 2 1 1 2 2 2
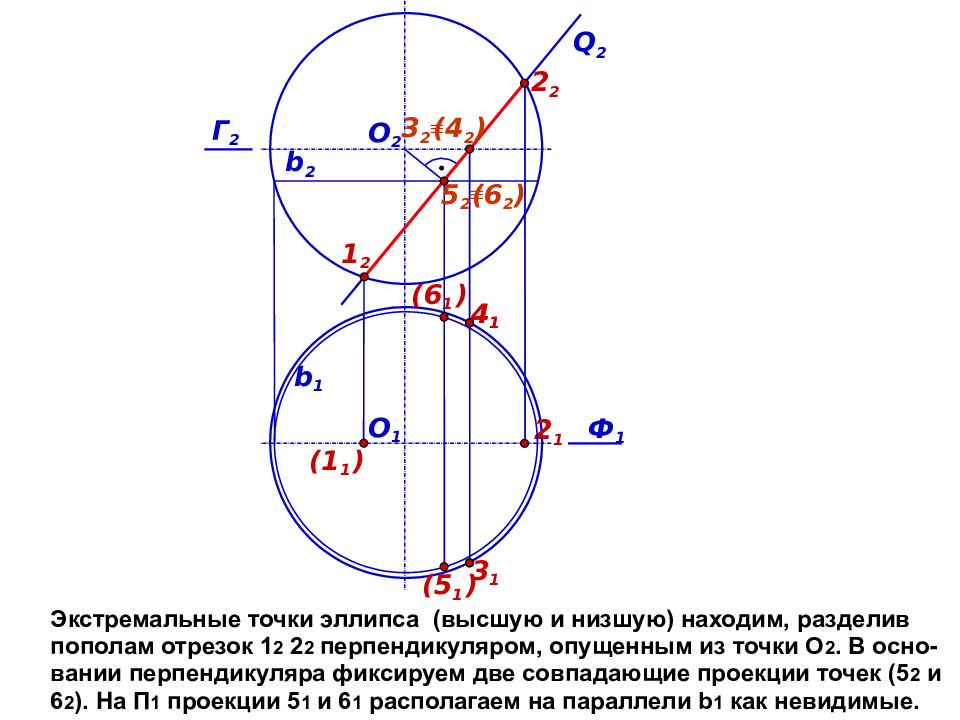
Экстремальные точки эллипса (высшую и низшую) находим, разделив пополам отрезок 1 2 2 2 перпендикуляром, опущенным из точки О 2. В осно- вании перпендикуляра фиксируем две совпадающие проекции точек (5 2 и 6 2 ). На П 1 проекции 5 1 и 6 1 располагаем на параллели b 1 как невидимые. Ф 1 Q 2 О 1 О 2 (1 1 ) 1 2 2 1 3 1 ( 4 2 ) 3 2 Г 2 4 1 b 2 4 1 b 1 2 2 (5 1 ) (6 1 ) (6 2 ) 5 2
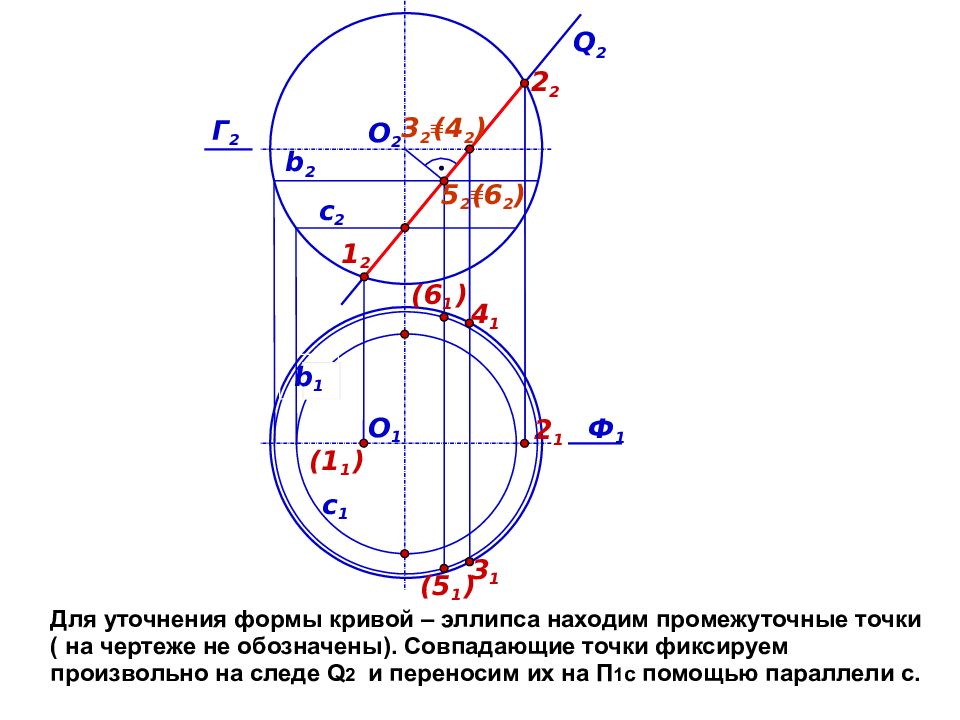
с 1 Для уточнения формы кривой – эллипса находим промежуточные точки ( на чертеже не обозначены). Совпадающие точки фиксируем произвольно на следе Q 2 и переносим их на П 1 с помощью параллели с. Ф 1 Q 2 О 2 (1 1 ) 1 2 (6 1 ) 2 1 Г 2 b 2 (5 1 ) (6 2 ) 5 2 b 1 2 2 с 2 3 1 4 1 О 1 ( 4 2 ) 3 2
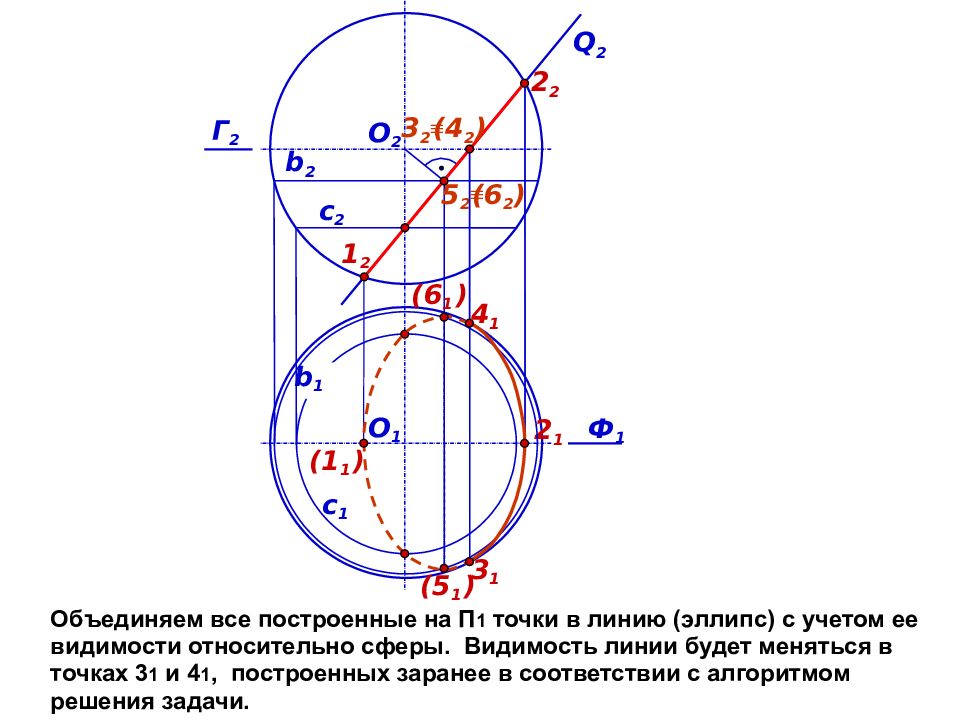
Объединяем все построенные на П 1 точки в линию (эллипс) с учетом ее видимости относительно сферы. Видимость линии будет меняться в точках 3 1 и 4 1, построенных заранее в соответствии с алгоритмом решения задачи. Ф 1 Q 2 с 1 О 2 (1 1 ) 1 2 (6 1 ) 2 1 Г 2 b 2 (5 1 ) (6 2 ) 5 2 b 1 2 2 с 2 3 1 4 1 ( 4 2 ) 3 2 О 1
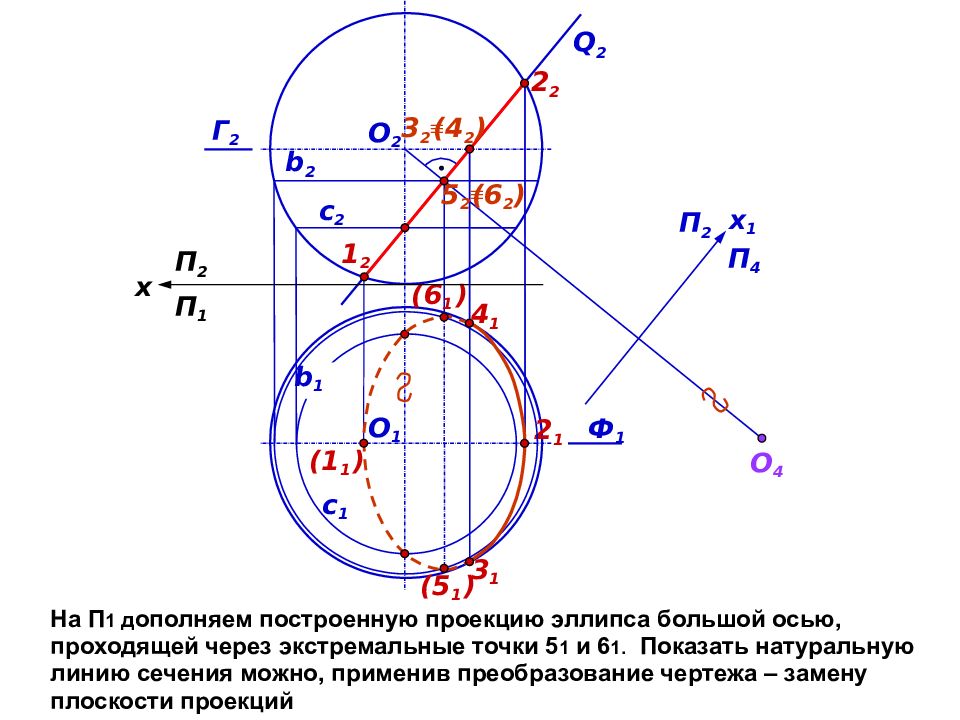
На П 1 д ополняем построенную проекцию эллипса большой осью, проходящей через экстремальные точки 5 1 и 6 1. Показать натуральную линию сечения можно, применив преобразование чертежа – замену плоскости проекций Ф 1 Q 2 с 1 О 2 (1 1 ) (6 1 ) 2 1 Г 2 b 2 (5 1 ) b 1 2 2 с 2 3 1 4 1 ( 4 2 ) 3 2 О 1 П 2 x 1 П 4 П 1 П 2 x (6 2 ) 5 2 1 2 О 4
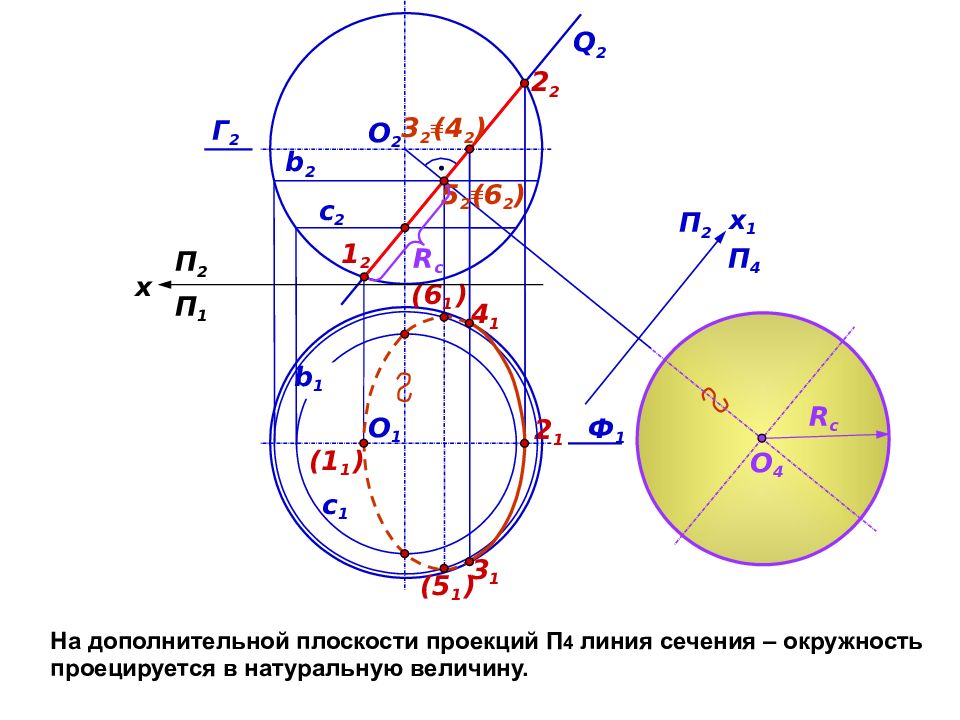
R c На дополнительной плоскости проекций П 4 линия сечения – окружность проецируется в натуральную величину. Ф 1 Q 2 с 1 О 2 (1 1 ) (6 1 ) 2 1 Г 2 b 2 (5 1 ) b 1 2 2 с 2 3 1 4 1 ( 4 2 ) 3 2 О 1 П 2 x 1 П 4 П 1 П 2 x О 4 (6 2 ) 5 2 R c 1 2
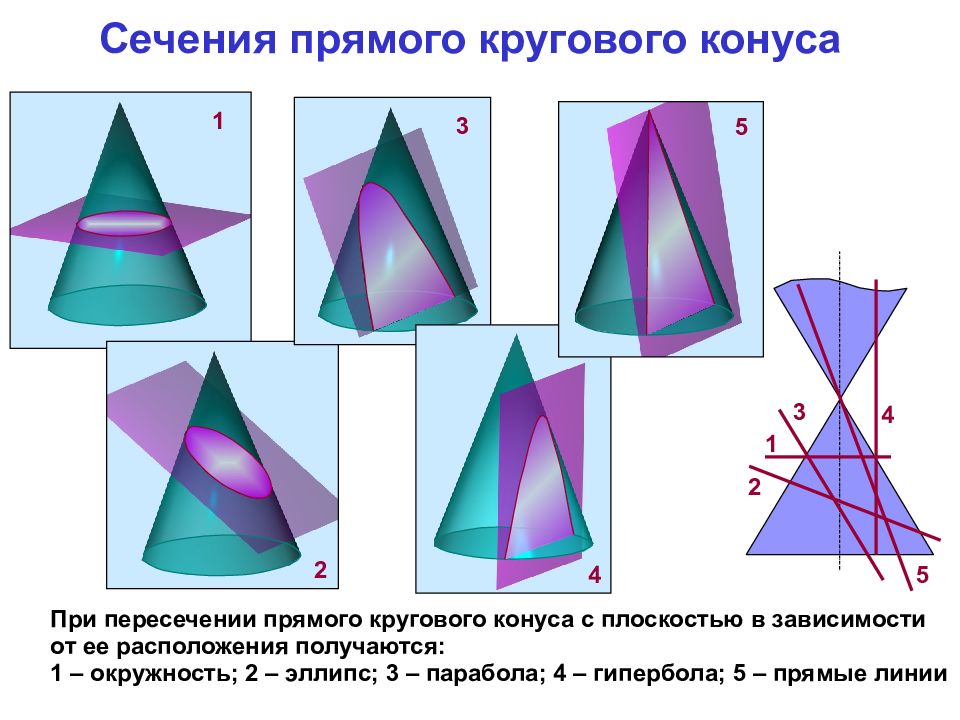
1 Сечения прямого кругового конуса При пересечении прямого кругового конуса с плоскостью в зависимости от ее расположения получаются: 1 – окружность; 2 – эллипс; 3 – парабола; 4 – гипербола; 5 – прямые линии 1 2 3 4 5 2 3 4 5
В сечении конической поверхности вращения плоскостью могут быть получены различные геометрические образы В плоскости Г – точка, Δ – окружность, Θ – эллипс, Σ – гипербола, Ф – парабола, Ψ – одна прямая, Ω – две прямые.
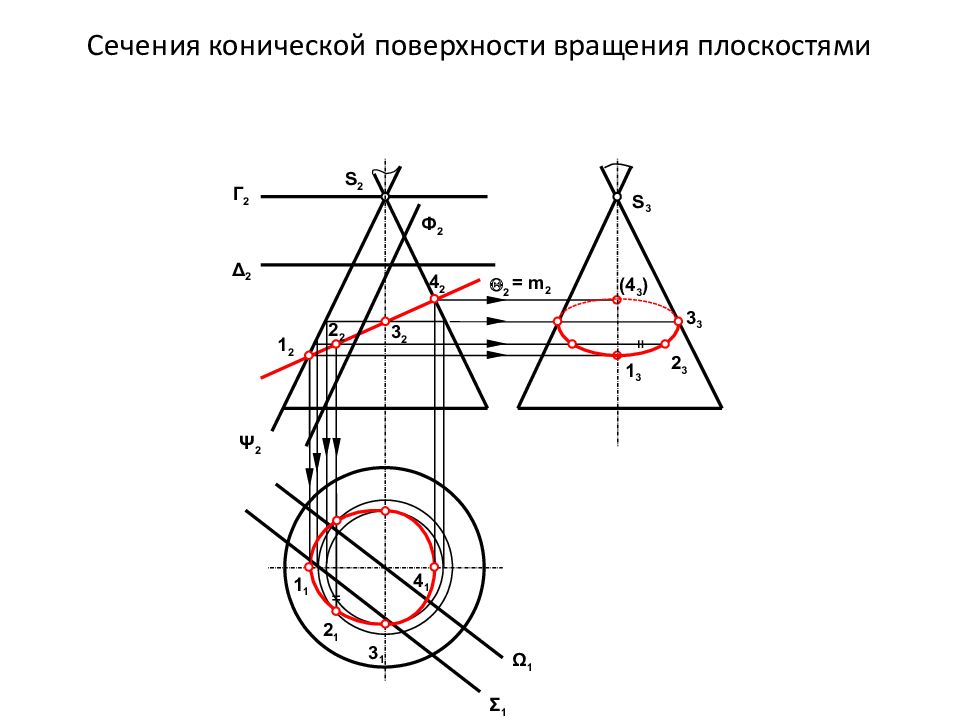
1 3 (4 3 ) Сечения конической поверхности вращения плоскостями S 3 S 2 Г 2 Δ 2 Ф 2 2 Ψ 2 Σ 1 Ω 1 S 1 = m 2 2 3 3 3 1 1 4 1 2 1 3 1 1 2 2 2 3 2 4 2
