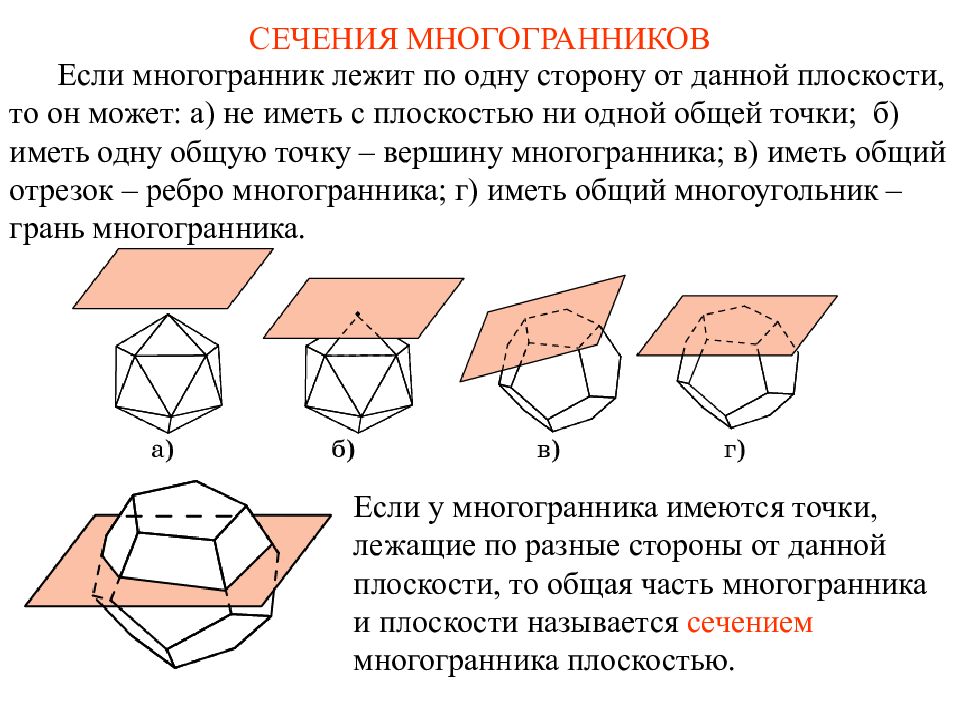
Первый слайд презентации: СЕЧЕНИЯ МНОГОГРАННИКОВ
Если многогранник лежит по одну сторону от данной плоскости, то он может: а) не иметь с плоскостью ни одной общей точки; б) иметь одну общую точку – вершину многогранника; в) иметь общий отрезок – ребро многогранника; г) иметь общий многоугольник – грань многогранника. Если у многогранника имеются точки, лежащие по разные стороны от данной плоскости, то общ ая часть многогранника и плоскости называе тся сечением многогранника плоскостью. СЕЧЕНИЯ МНОГОГРАННИКОВ
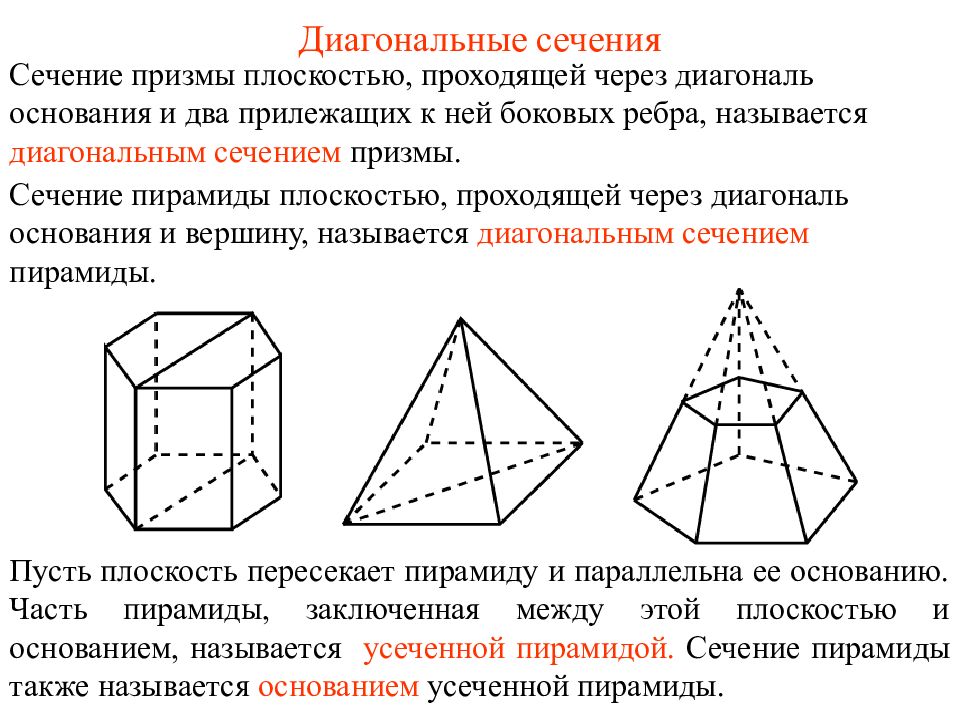
Слайд 2: Диагональные сечения
Сечение призмы плоскостью, проходящей через диагональ основания и два прилежащих к ней боковых ребра, называется диагональным сечением призмы. Сечение пирамиды плоскостью, проходящей через диагональ основания и вершину, называется диагональным сечением пирамиды. Диагональные сечения Пусть плоскость пересекает пирамиду и параллельна ее основанию. Часть пирамиды, заключенная между этой плоскостью и основанием, называется усеченной пирамидой. Сечение пирамиды также называется основанием усеченной пирамиды.
Слайд 3: Упражнение 1
Какой фигурой может быть сечение многогранника плоскостью? Упражнение 1 Ответ: Многоугольником или объединением нескольких многоугольников.
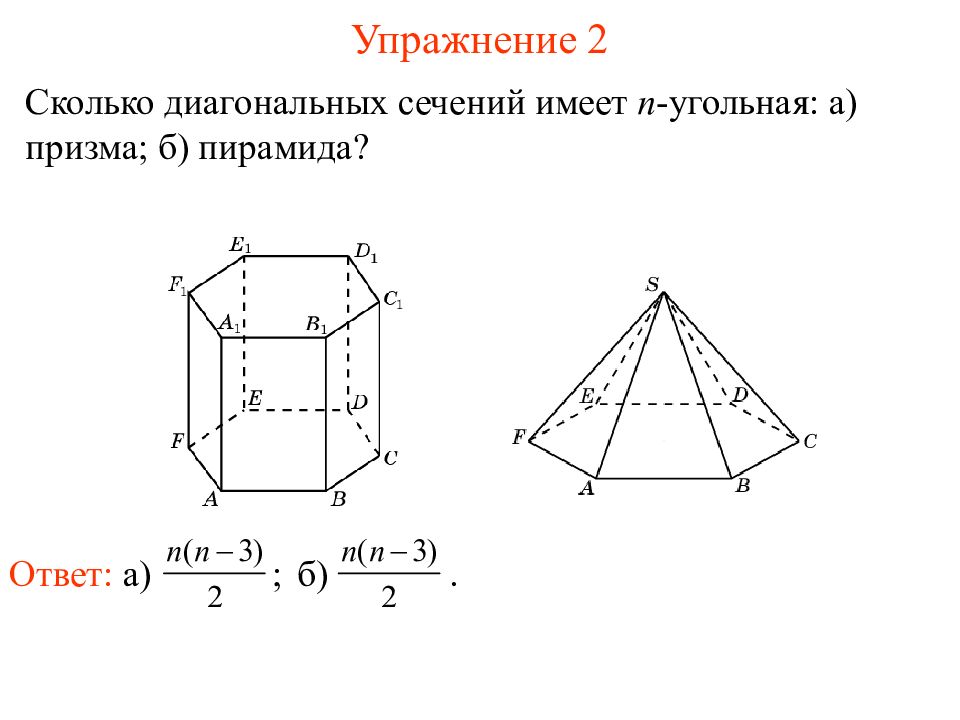
Слайд 4: Упражнение 2
Сколько диагональных сечений имеет n -угольная: а) призма; б) пирамида? Упражнение 2 Ответ: а) ; б).
Слайд 5: Упражнение 3
Может ли в сечении куба плоскостью получиться: а) треугольник ? Упражнение 3 Ответ: а) Да; б) правильный треугольник ? в) равнобедренный треугольник ? г) прямоугольный треугольник ? д) тупоугольный треугольник ? в) да; г) нет; д) нет. б) да;
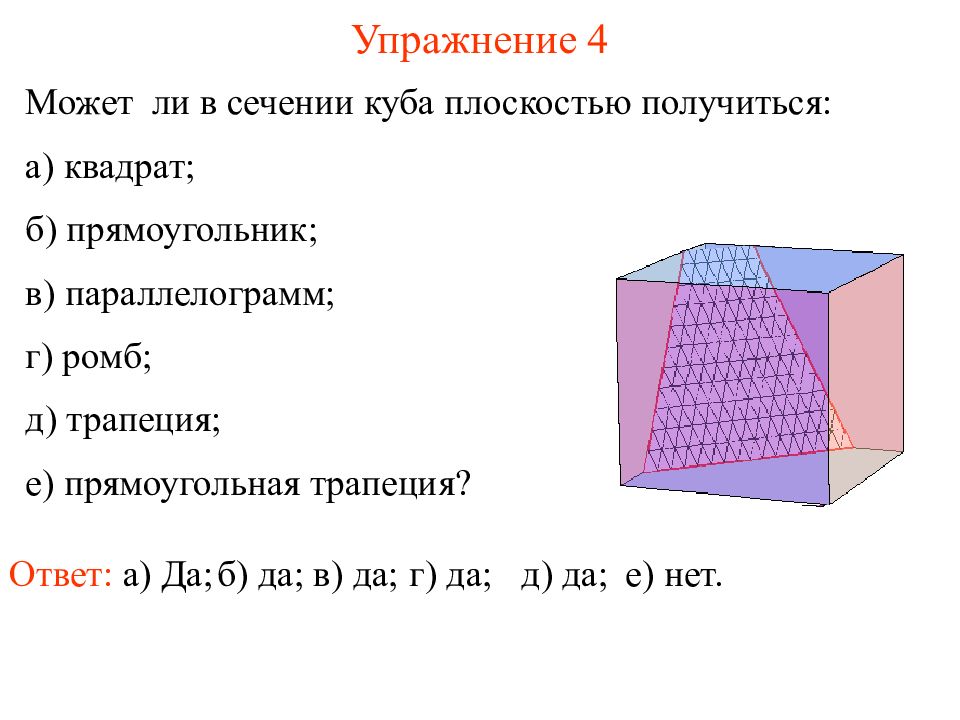
Слайд 6: Упражнение 4
Может ли в сечении куба плоскостью получиться: а) квадрат; б) прямоугольник; в) параллелограмм; г) ромб; д) трапеция; е) прямоугольная трапеция? Упражнение 4 Ответ: а) Да; б) да; в) да; е) нет. г) да; д) да;
Слайд 7: Упражнение 5
Может ли в сечении куба плоскостью получиться: а) пятиугольник; б) правильный пятиугольник? Упражнение 5 б) нет. У пятиугольников, которые получаются в сечении куба, имеются две пары параллельных сторон, а у правильного пятиугольника таких сторон нет. Ответ: а) Да;
Слайд 8: Упражнение 6
Может ли в сечении куба плоскостью получиться: а) шестиугольник; б) правильный шестиугольник; в) многоугольник с числом сторон больше шести? Упражнение 6 Ответ: а) Да; в) нет. б) да;
Слайд 9: Упражнение 7
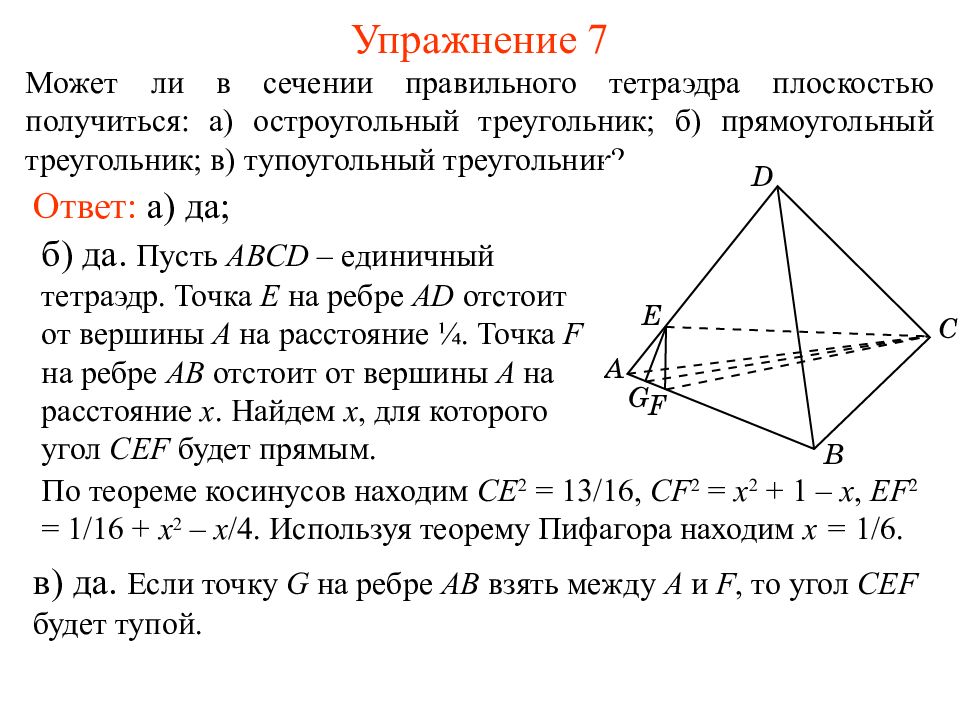
Может ли в сечении правильного тетраэдра плоскостью получиться : а) остроугольный треугольник; б) прямоугольный треугольник; в) тупоугольный треугольник ? Упражнение 7 Ответ: а) да; б) да. Пусть ABCD – единичный тетраэдр. Точка E на ребре AD отстоит от вершины A на расстояние ¼. Точка F на ребре AB отстоит от вершины A на расстояние x. Найдем x, для которого угол CEF будет прямым. По теореме косинусов находим CE 2 = 13/16, CF 2 = x 2 + 1 – x, EF 2 = 1/16 + x 2 – x /4. Используя теорему Пифагора находим x = 1/6. в) да. Если точку G на ребре AB взять между A и F, то угол CEF будет тупой.
Слайд 10: Упражнение 8
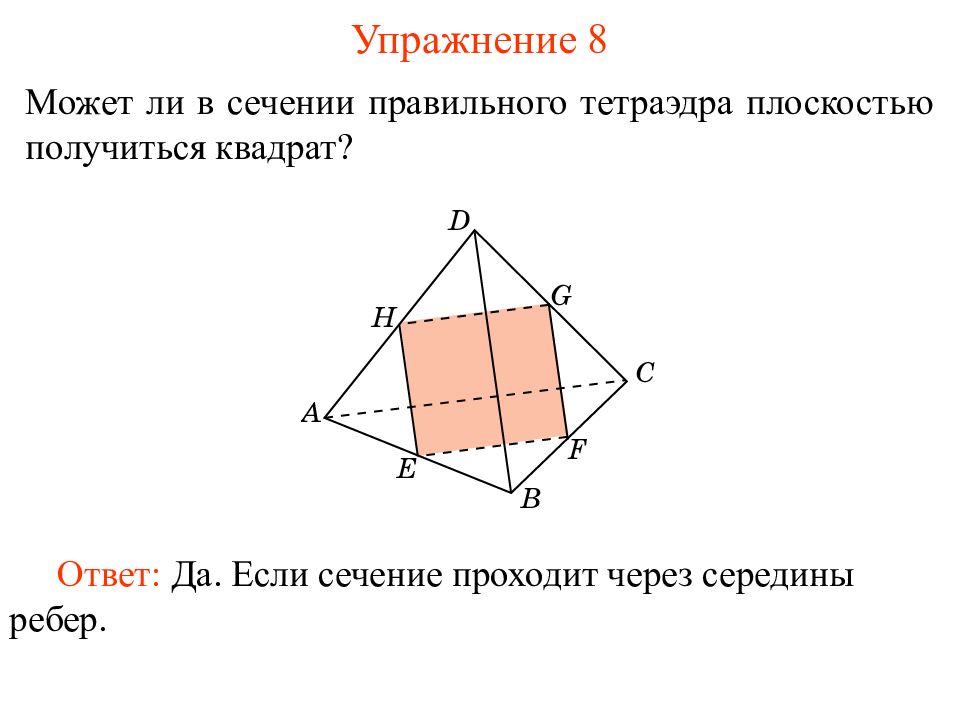
Может ли в сечении правильного тетраэдра плоскостью получиться квадрат? Упражнение 8 Ответ: Да. Если сечение проходит через середины ребер.
Слайд 11: Упражнение 9
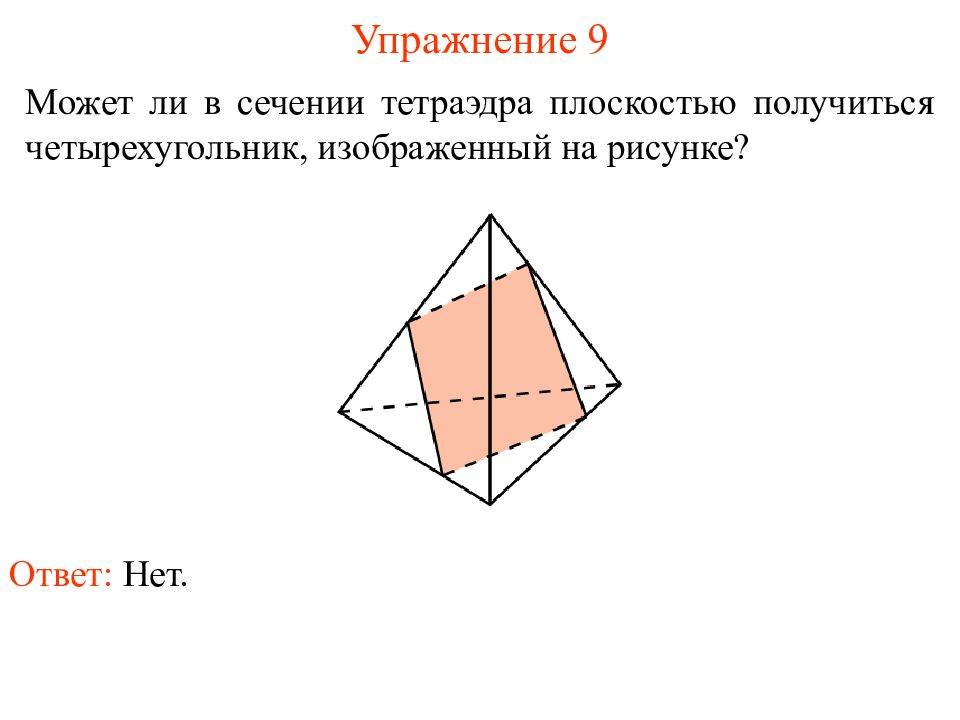
Может ли в сечении тетраэдра плоскостью получиться четырехугольник, изображенный на рисунке ? Упражнение 9 Ответ: Нет.
Слайд 12: Упражнение 10
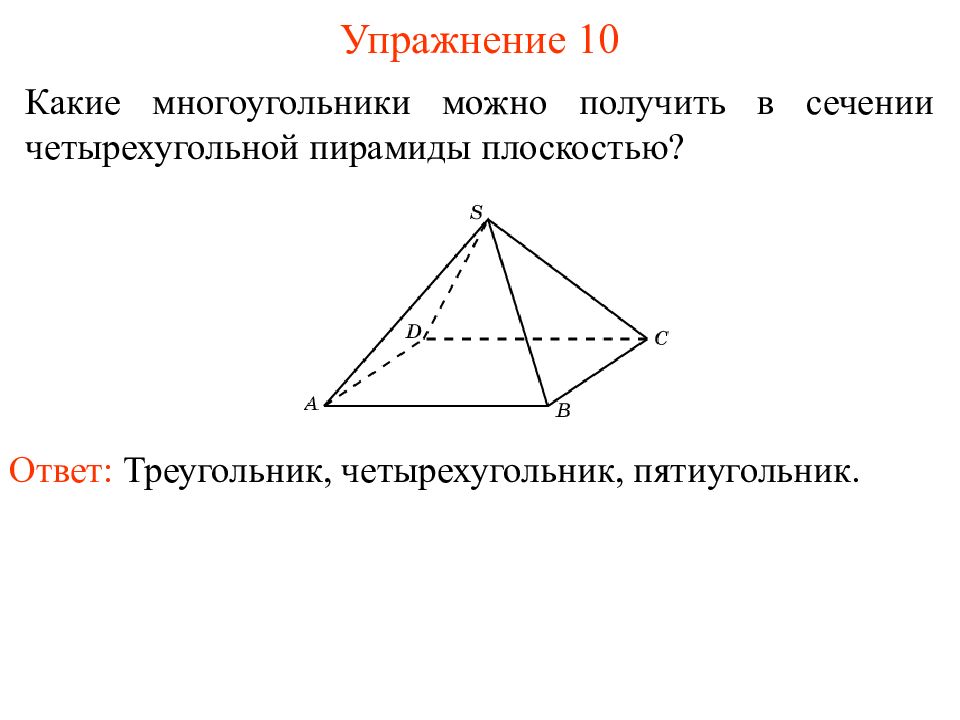
Какие многоугольники можно получить в сечении четырехугольной пирамиды плоскостью? Упражнение 10 Ответ: Треугольник, четырехугольник, пятиугольник.
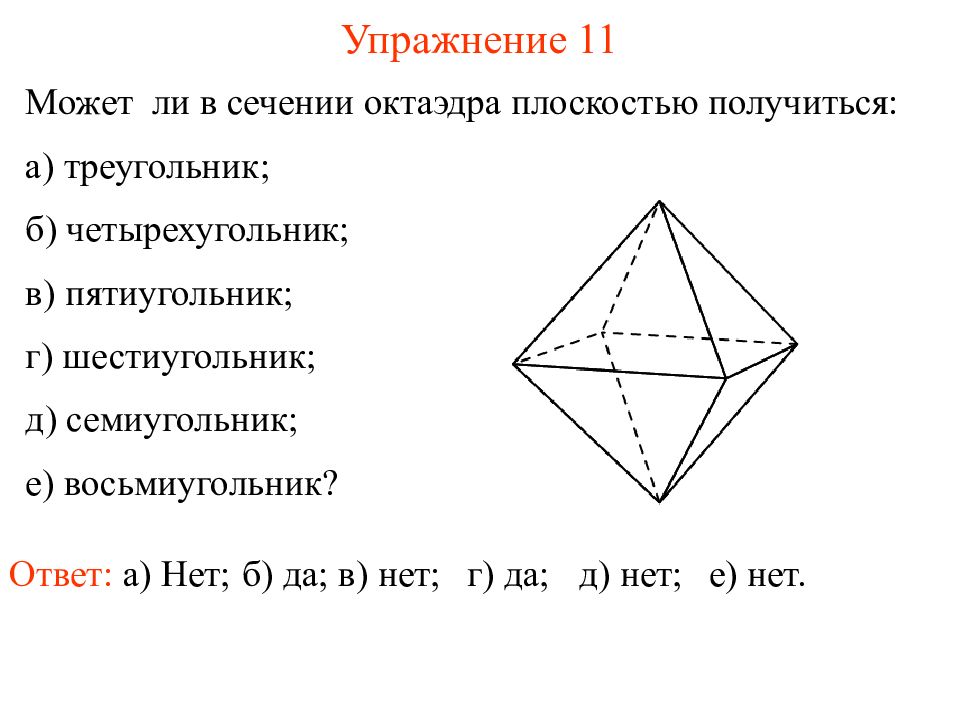
Слайд 13: Упражнение 11
Может ли в сечении октаэдра плоскостью получиться: а) треугольник; б) четырехугольник; в) пятиугольник; г) шестиугольник; д) семиугольник; е) восьмиугольник? Упражнение 11 Ответ: а) Нет; б) да; в) нет; г) да; д) нет; е) нет.
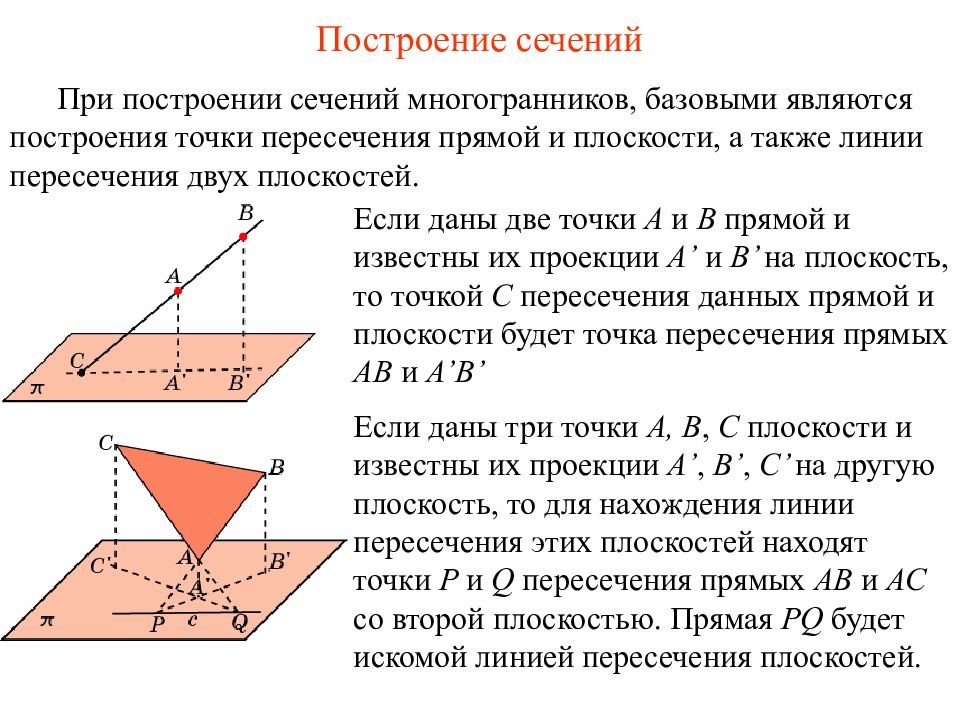
Слайд 14: Построение сечений
При построении сечений многогранников, базовыми являются построения точки пересечения прямой и плоскости, а также линии пересечения двух плоскостей. Если даны две точки A и B прямой и известны их проекции A’ и B’ на плоскость, то точкой С пересечения данных прямой и плоскости будет точка пересечения прямых AB и A’B’ Если даны три точки A, B, C плоскости и известны их проекции A’, B’, C’ на другую плоскость, то для нахождения линии пересечения этих плоскостей находят точки P и Q пересечения прямых AB и AC со второй плоскостью. Прямая PQ будет искомой линией пересечения плоскостей. Построение сечений
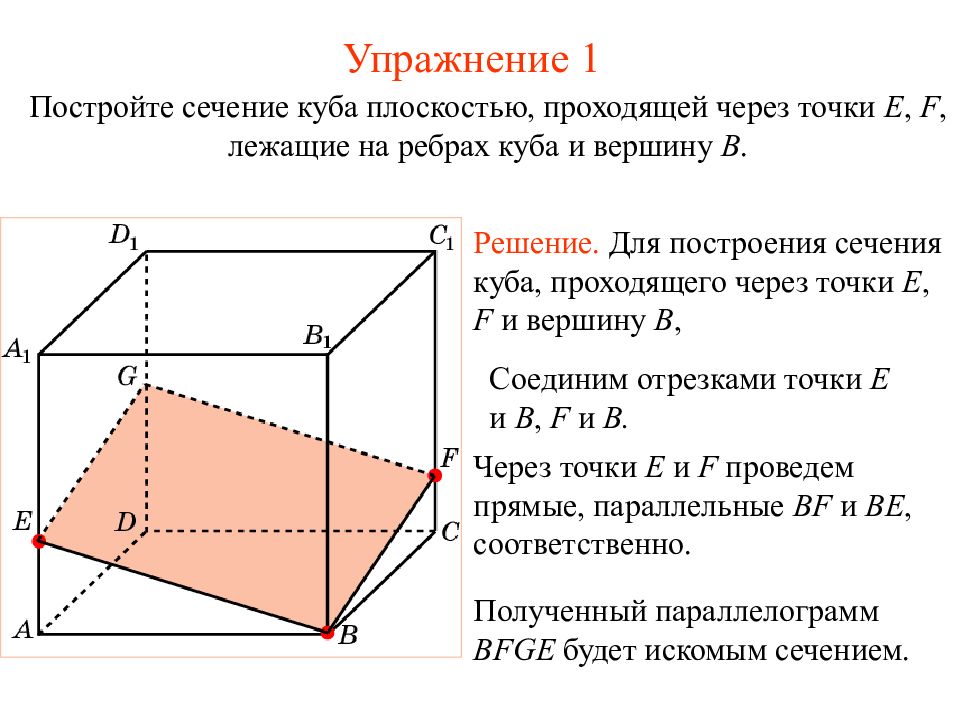
Слайд 15: Упражнение 1
Решение. Для построения сечения куба, проходящего через точки E, F и вершину B, Постройте сечение куба плоскостью, проходящей через точки E, F, лежащие на ребрах куба и вершину B. Соединим отрезками точки E и B, F и B. Через точки E и F проведем прямые, параллельные BF и BE, соответственно. Полученный параллелограмм BFGE будет искомым сечением. Упражнение 1
Слайд 16: Упражнение 2
Решение. Для построения сечения куба, проходящего через точки E, F, G, проведем прямую EF и обозначим P её точку пересечения с AD. Обозначим Q точку пересечения прямых PG и AB. Соединим точки E и Q, F и G. Постройте сечение куба плоскостью, проходящей через точки E, F, G, лежащие на ребрах куба. Полученная трапеция EFGQ будет искомым сечением. Упражнение 2
Слайд 17: Упражнение 3
Решение. Для построения сечения куба, проходящего через точки E, F, G, проведем прямую EF и обозначим P её точку пересечения с AD. Обозначим Q, R точки пересечения прямой PG с AB и DC. Соединим точки E и Q, G и S. Постройте сечение куба плоскостью, проходящей через точки E, F, G, лежащие на ребрах куба. Полученный пятиугольник EFSGQ будет искомым сечением. Обозначим S точку пересечения FR c СС 1. Упражнение 3
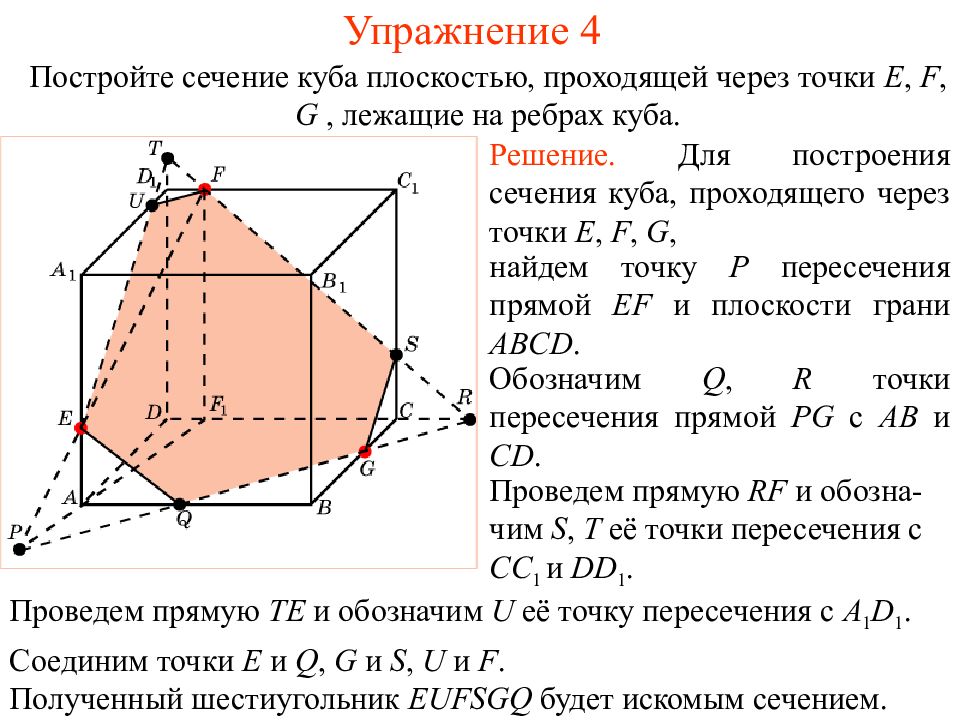
Слайд 18: Упражнение 4
Решение. Для построения сечения куба, проходящего через точки E, F, G, найдем точку P пересечения прямой EF и плоскости грани ABCD. Проведем прямую RF и обозна - чим S, T её точки пересечения с CC 1 и DD 1. Обозначим Q, R точки пересечения прямой PG с AB и CD. Постройте сечение куба плоскостью, проходящей через точки E, F, G, лежащие на ребрах куба. Соединим точки E и Q, G и S, U и F. Проведем прямую TE и обозначим U её точку пересечения с A 1 D 1. Полученный шестиугольник EUFSGQ будет искомым сечением. Упражнение 4
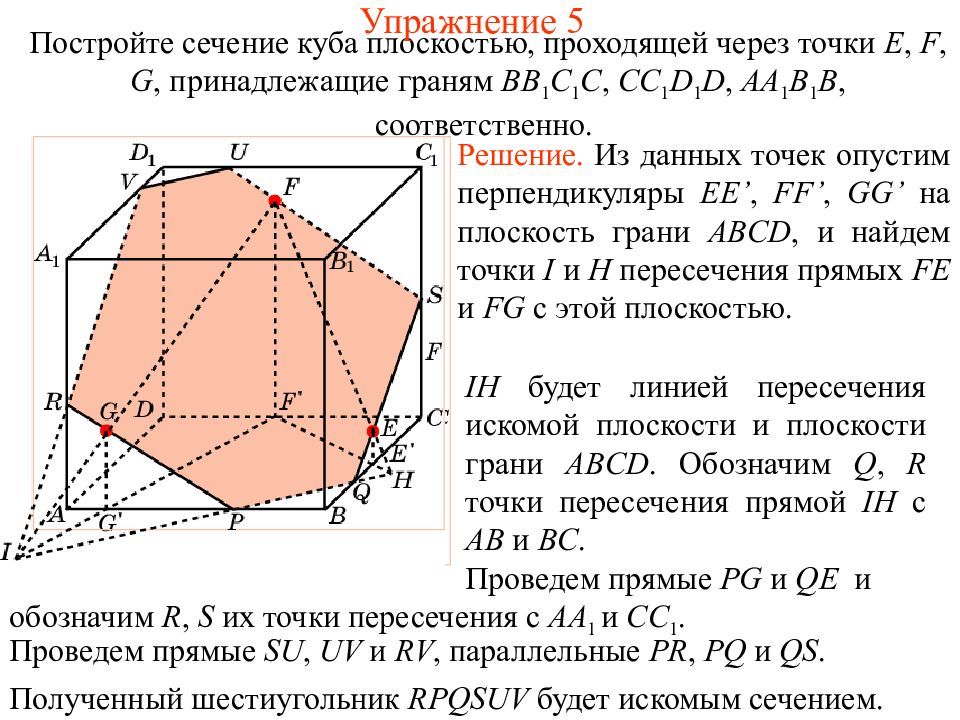
Слайд 19: Упражнение 5
Постройте сечение куба плоскостью, проходящей через точки E, F, G, принадлежащие граням BB 1 C 1 C, CC 1 D 1 D, AA 1 B 1 B, соответственно. Решение. Из данных точек опустим перпендикуляры EE’, FF’, GG’ на плоскость грани ABCD, и найдем точки I и H пересечения прямых FE и FG с этой плоскостью. IH будет линией пересечения искомой плоскости и плоскости грани ABCD. Обозначим Q, R точки пересечения прямой IH с AB и BC. Проведем прямые PG и QE и обозначим R, S их точки пересечения с AA 1 и CC 1. Проведем прямые SU, UV и RV, параллельные PR, PQ и QS. Полученный шестиугольник RPQSUV будет искомым сечением. Упражнение 5
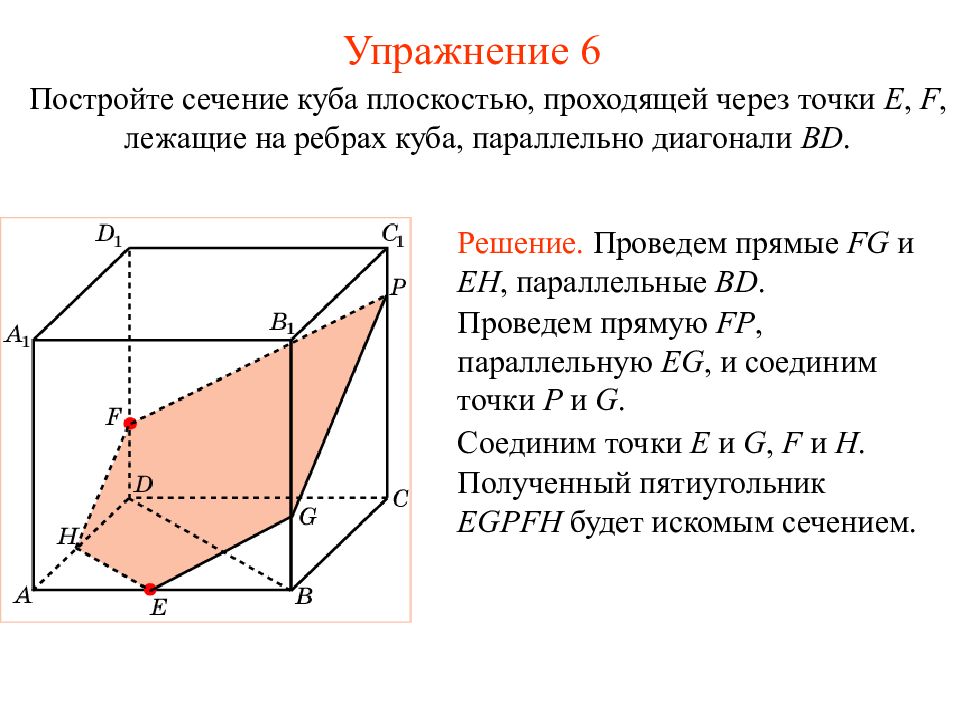
Слайд 20: Упражнение 6
Постройте сечение куба плоскостью, проходящей через точки E, F, лежащие на ребрах куба, параллельно диагонали BD. Решение. Проведем прямые FG и EH, параллельные BD. Проведем прямую FP, параллельную EG, и соединим точки P и G. Соединим точки E и G, F и H. Полученный пятиугольник EGPFH будет искомым сечением. Упражнение 6
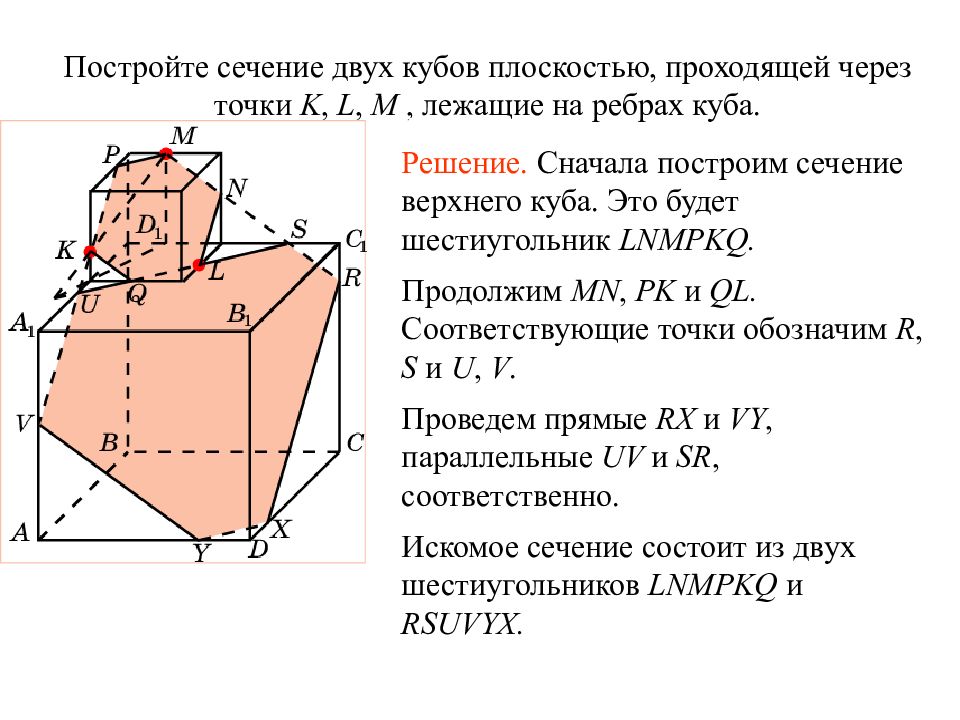
Слайд 21: Упражнение 7
Постройте сечение двух кубов плоскостью, проходящей через точки K, L, M, лежащие на ребрах куба. Решение. Сначала построим сечение верхнего куба. Это будет шестиугольник LNMPKQ. Продолжим MN, PK и QL. Соответствующие точки обозначим R, S и U, V. Проведем прямые RX и VY, параллельные UV и SR, соответственно. Искомое сечение состоит из двух шестиугольников LNMPKQ и RSUVYX. Упражнение 7
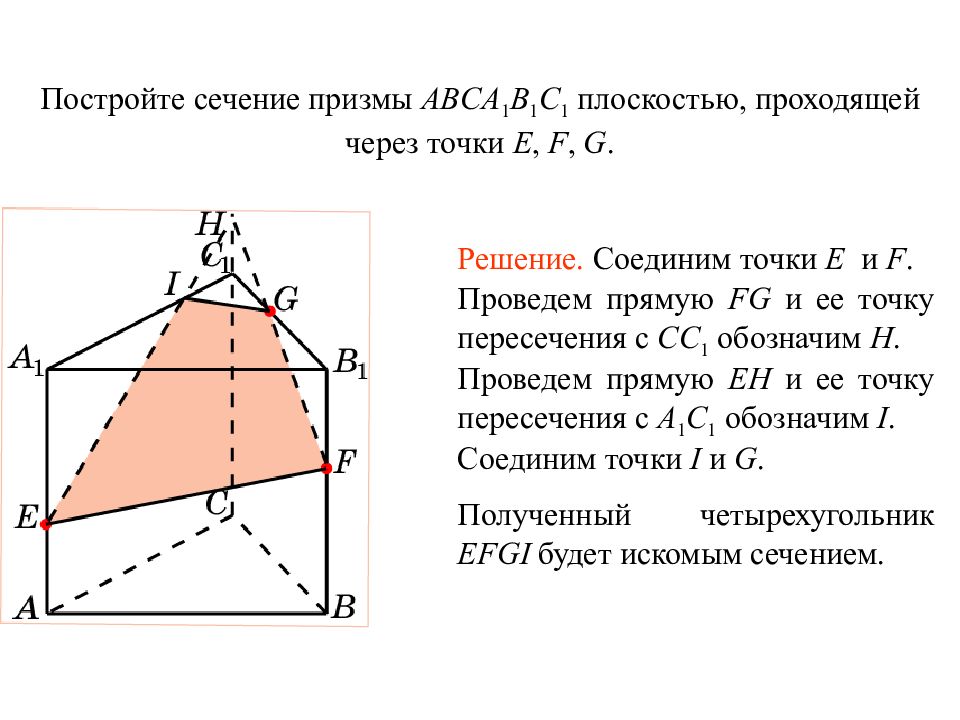
Слайд 22: Упражнение 8
Постройте сечение призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки E, F, G. Решение. Соединим точки E и F. Проведем прямую FG и ее точку пересечения с CC 1 обозначим H. Проведем прямую EH и ее точку пересечения с A 1 C 1 обозначим I. Соединим точки I и G. Полученный четырехугольник EFGI будет искомым сечением. Упражнение 8
Слайд 23: Упражнение 9
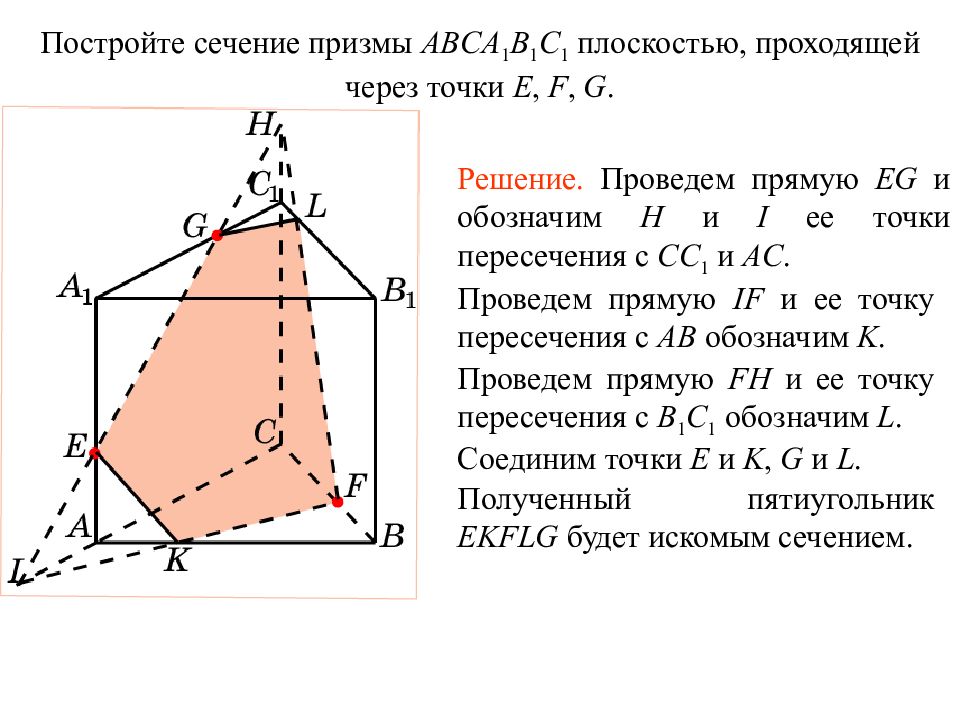
Постройте сечение призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки E, F, G. Решение. Проведем прямую EG и обозначим H и I ее точки пересечения с CC 1 и AC. Проведем прямую IF и ее точку пересечения с AB обозначим K. Проведем прямую FH и ее точку пересечения с B 1 C 1 обозначим L. Соединим точки E и K, G и L. Полученный пятиугольник EKFLG будет искомым сечением. Упражнение 9
Слайд 24: Упражнение 1 0
Постройте сечение призмы ABCA 1 B 1 C 1 плоскостью, параллельной AC 1, проходящей через точки D и D 1. Упражнение 1 0 Решение. Через точку D проведем прямую параллельную AC 1 и обозначим E ее точку пересечения с прямой BC 1. Эта точка будет принадлежать плоскости грани ADD 1 A 1. Проведем прямую DE и обозначим F ее точку пересечения с ребром BC. Соединим отрезком точки F и D. Через точку D проведем прямую параллельную прямой FD и обозначим G точку ее пересечения с ребром A 1 C 1, H – точку ее пересечения с прямой A 1 B 1. Проведем прямую DH и обозначим P ее точку пересечения с ребром AA 1. Соединим отрезком точки P и G. Полученный четырехугольник EFIK будет искомым сечением.
Слайд 25: Упражнение 1 1
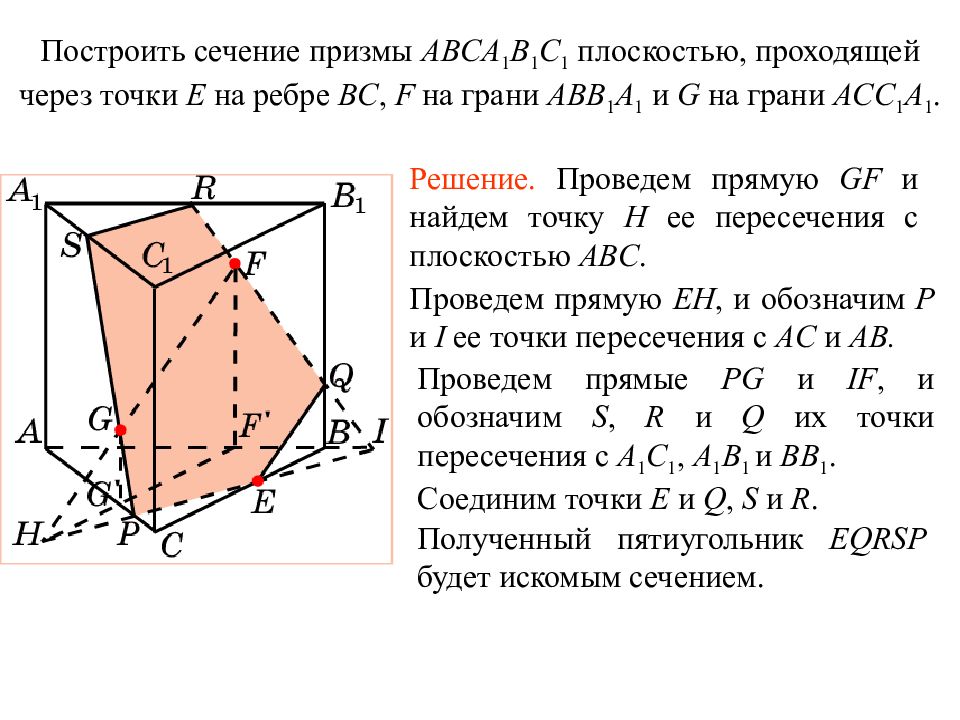
Построить сечение призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки E на ребре BC, F на грани ABB 1 A 1 и G на грани ACC 1 A 1. Решение. Проведем прямую GF и найдем точку H ее пересечения с плоскостью ABC. Проведем прямую EH, и обозначим P и I ее точки пересечения с AC и AB. Проведем прямые PG и IF, и обозначим S, R и Q их точки пересечения с A 1 C 1, A 1 B 1 и BB 1. Соединим точки E и Q, S и R. Полученный пятиугольник EQRSP будет искомым сечением. Упражнение 1 1
Слайд 26: Упражнение 1 2
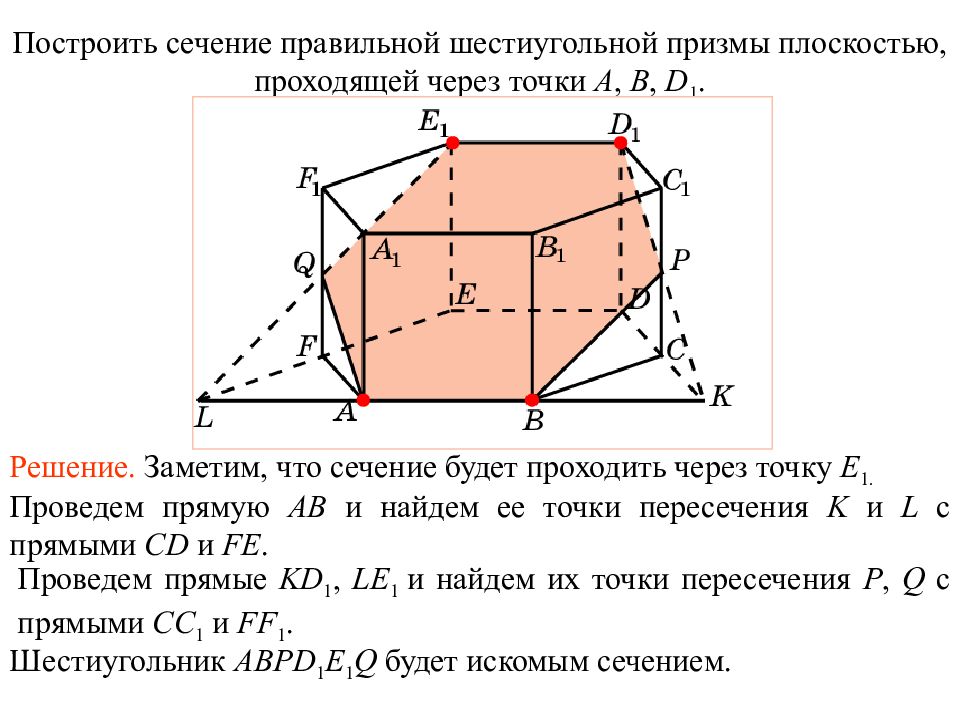
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки A, B, D 1. Решение. Заметим, что сечение будет проходить через точку E 1. Проведем прямую AB и найдем ее точки пересечения K и L с прямыми CD и FE. Проведем прямые KD 1, LE 1 и найдем их точки пересечения P, Q с прямыми CC 1 и FF 1. Шестиугольник ABPD 1 E 1 Q будет искомым сечением. Упражнение 1 2
Слайд 27: Упражнение 1 3
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки A, B’, F’. Решение. Проведем отрезки AB’ и AF’. Через точку B’ проведем прямую, параллельную AF’, и ее точку пересечения с EE 1 обозначим E’. Через точку F’ проведем прямую, параллельную AB’, и ее точку пересечения с CC 1 обозначим C’. Через точки E’ и C’ проведем прямые, параллельные AB’ и AF’, и их точки пересечения с D 1 E 1 и C 1 D 1 обозначим D’, D”. Соединим точки B’, C’ ; D’, D” ; F’, E’. Полученный семиугольник AB’C’D”D’E’F’ будет искомым сечением. Упражнение 1 3
Слайд 28: Упражнение 1 4
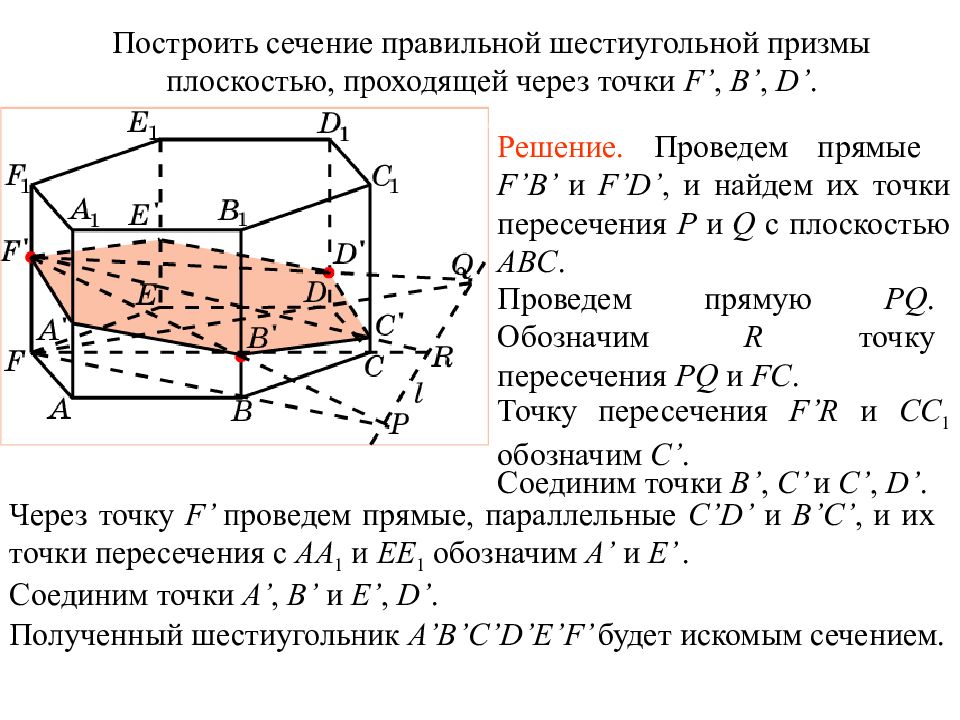
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки F’, B’, D’. Решение. Проведем прямые F’B’ и F’D’, и найдем их точки пересечения P и Q с плоскостью ABC. Проведем прямую PQ. Обозначим R точку пересечения PQ и FC. Точку пересечения F’R и CC 1 обозначим C’. Соединим точки B’, C’ и C’, D’. Через точку F’ проведем прямые, параллельные C’D’ и B’C’, и их точки пересечения с AA 1 и EE 1 обозначим A’ и E’. Соединим точки A’, B’ и E’, D’. Полученный шестиугольник A’B’C’D’E’F’ будет искомым сечением. Упражнение 1 4
Слайд 29: Упражнение 1 5
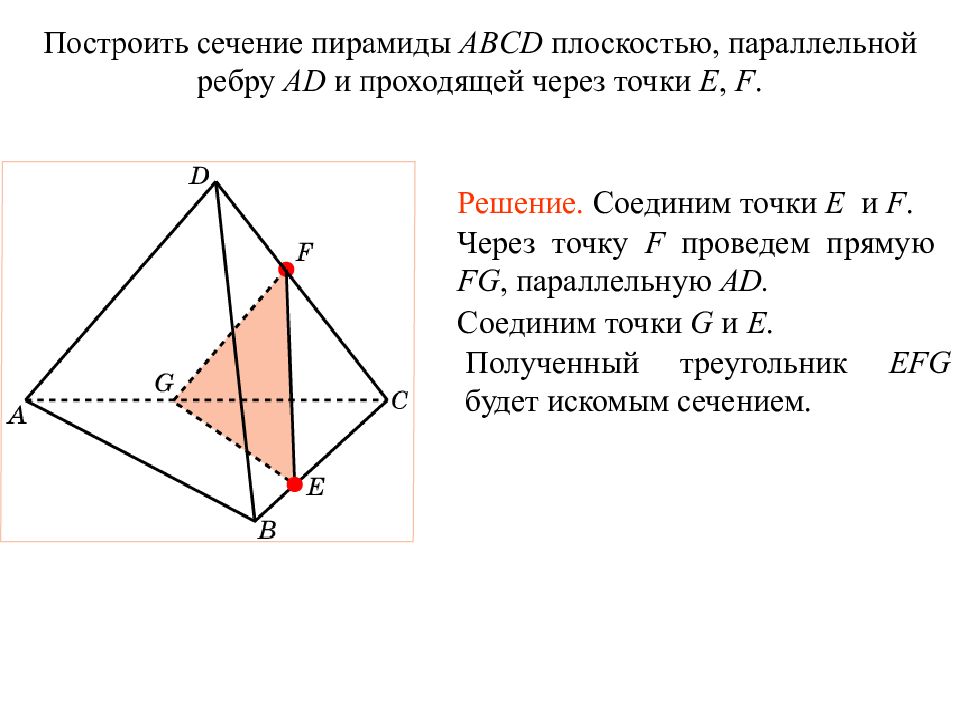
Построить сечение пирамиды ABCD плоскостью, параллельной ребру AD и проходящей через точки E, F. Решение. Соединим точки E и F. Через точку F проведем прямую FG, параллельную AD. Соединим точки G и E. Полученный треугольник EFG будет искомым сечением. Упражнение 1 5
Слайд 30: Упражнение 1 6
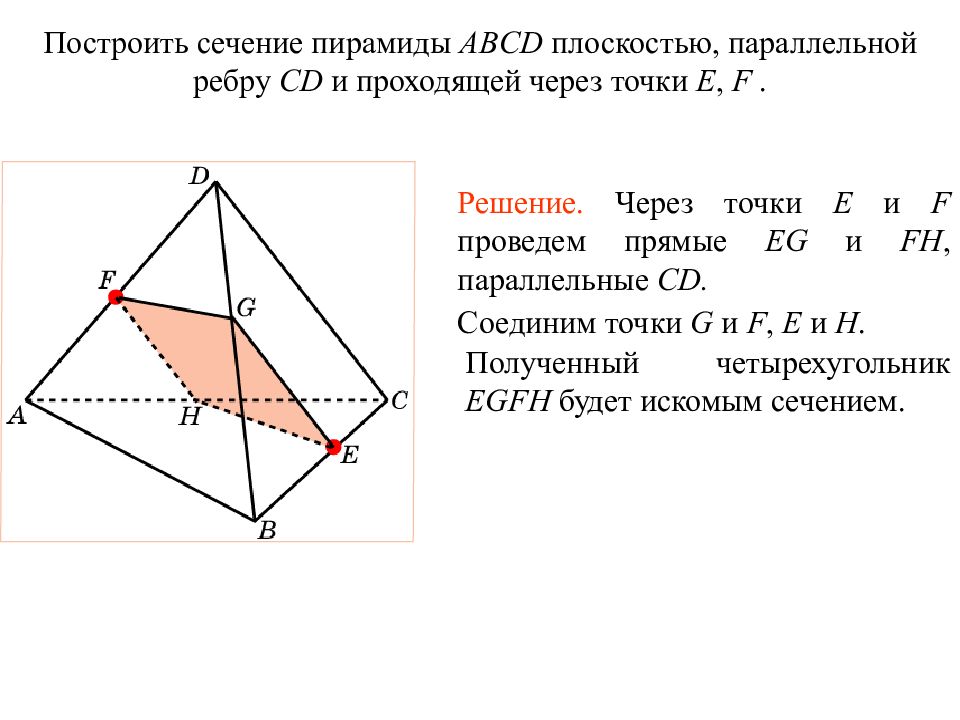
Построить сечение пирамиды ABCD плоскостью, параллельной ребру CD и проходящей через точки E, F. Решение. Через точки E и F проведем прямые EG и FH, параллельные CD. Соединим точки G и F, E и H. Полученный четырехугольник EGFH будет искомым сечением. Упражнение 1 6
Слайд 31: Упражнение 17
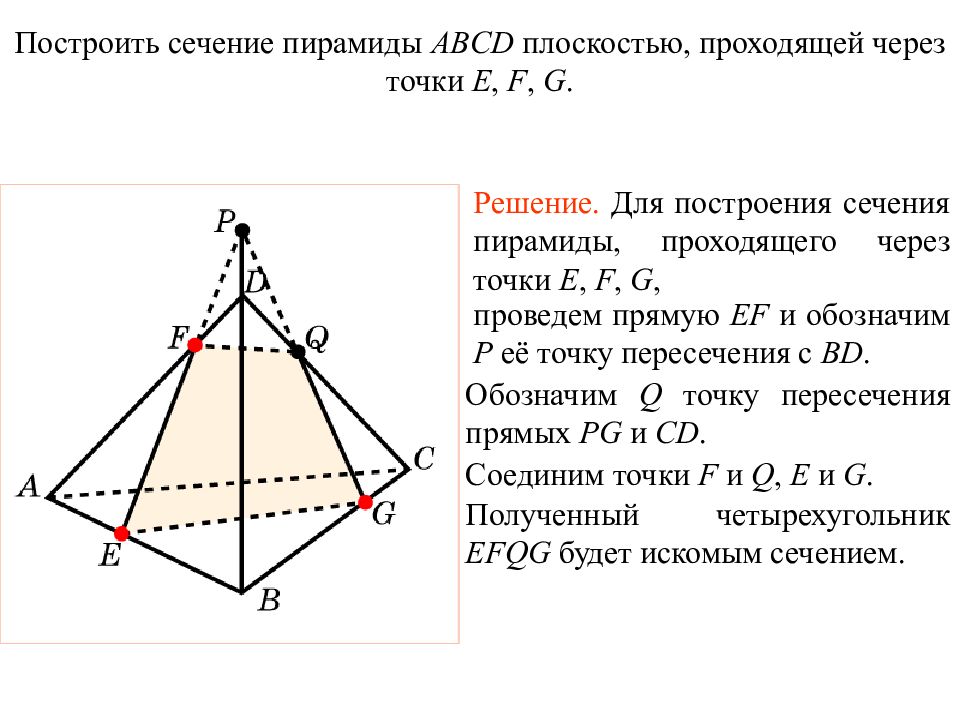
Решение. Для построения сечения пирамиды, проходящего через точки E, F, G, проведем прямую EF и обозначим P её точку пересечения с BD. Обозначим Q точку пересечения прямых PG и CD. Соединим точки F и Q, E и G. Построить сечение пирамиды ABCD плоскостью, проходящей через точки E, F, G. Полученный четырехугольник EFQG будет искомым сечением. Упражнение 17
Слайд 32: Упражнение 18
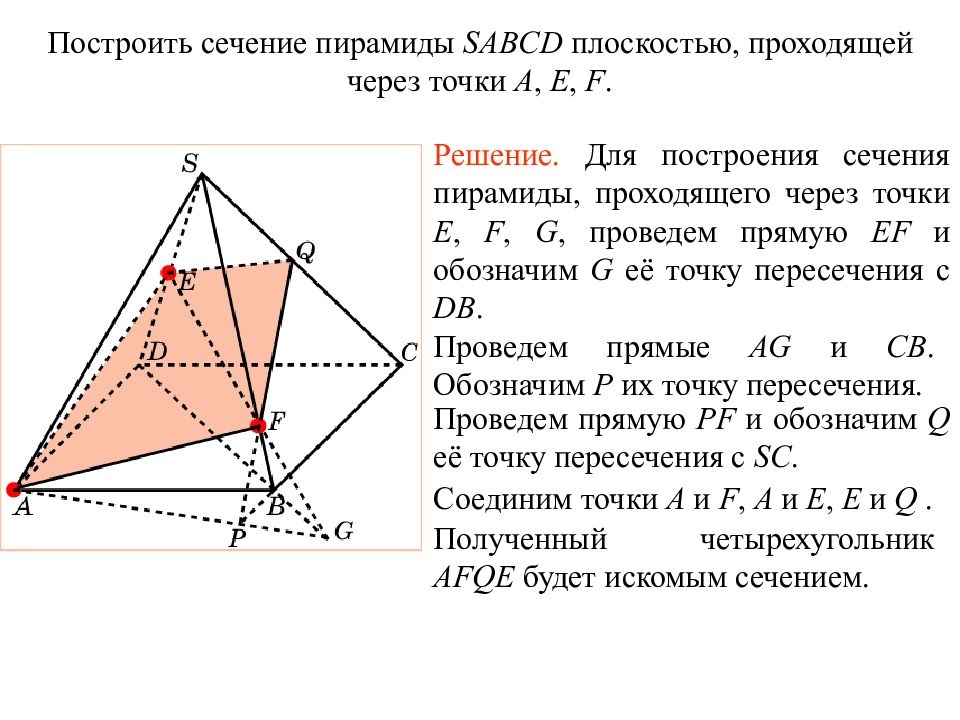
Построить сечение пирамиды SABCD плоскостью, проходящей через точки A, E, F. Решение. Для построения сечения пирамиды, проходящего через точки E, F, G, проведем прямую EF и обозначим G её точку пересечения с DB. Проведем прямые AG и CB. Обозначим P их точку пересечения. Проведем прямую PF и обозначим Q её точку пересечения с SC. Соединим точки A и F, A и E, E и Q. Полученный четырехугольник AFQE будет искомым сечением. Упражнение 18
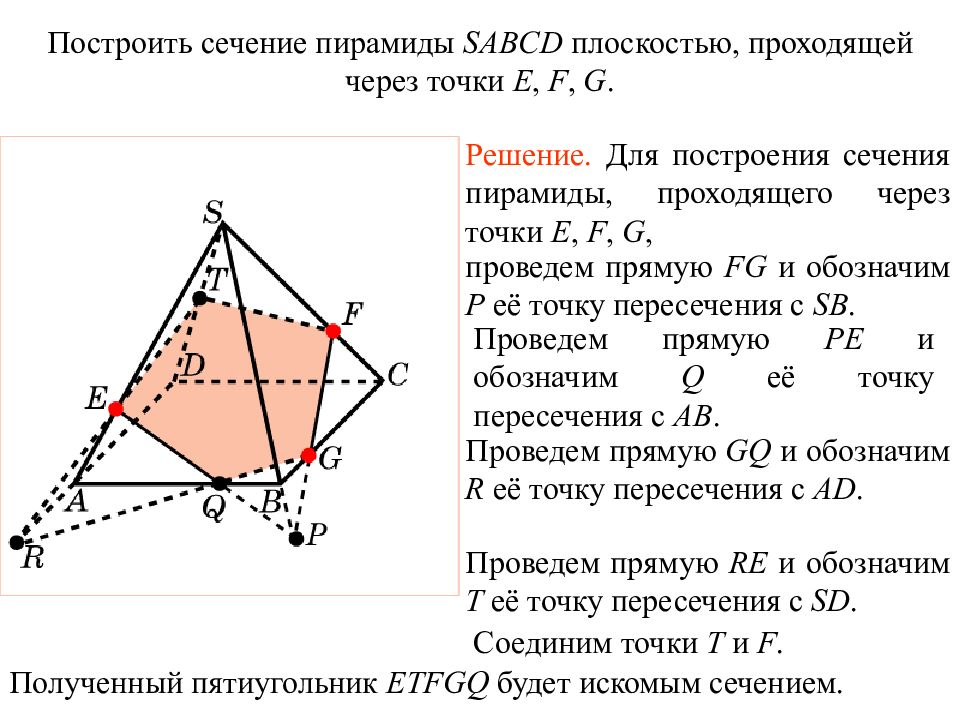
Слайд 33: Упражнение 19
Решение. Для построения сечения пирамиды, проходящего через точки E, F, G, проведем прямую FG и обозначим P её точку пересечения с SB. Проведем прямую PE и обозначим Q её точку пересечения с AB. Построить сечение пирамиды SABCD плоскостью, проходящей через точки E, F, G. Полученный пятиугольник ETFGQ будет искомым сечением. Соединим точки T и F. Проведем прямую GQ и обозначим R её точку пересечения с AD. Проведем прямую RE и обозначим T её точку пересечения с SD. Упражнение 19
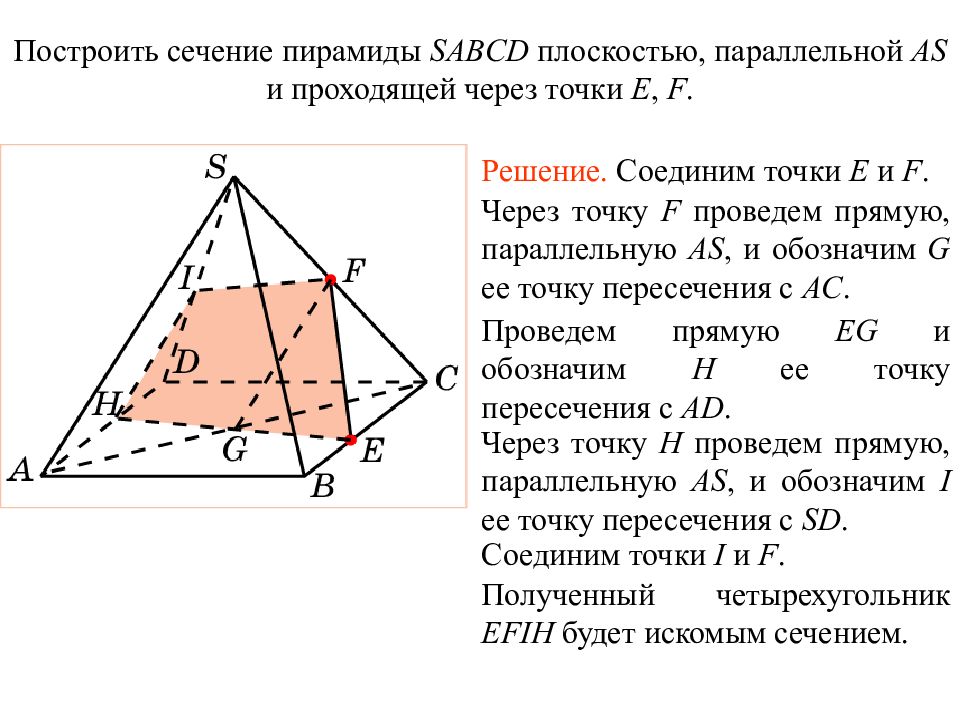
Слайд 34: Упражнение 2 0
Построить сечение пирамиды SABCD плоскостью, параллельной AS и проходящей через точки E, F. Решение. Соединим точки E и F. Через точку F проведем прямую, параллельную AS, и обозначим G ее точку пересечения с AC. Проведем прямую EG и обозначим H ее точку пересечения с AD. Через точку H проведем прямую, параллельную AS, и обозначим I ее точку пересечения с SD. Соединим точки I и F. Полученный четырехугольник EFIH будет искомым сечением. Упражнение 2 0
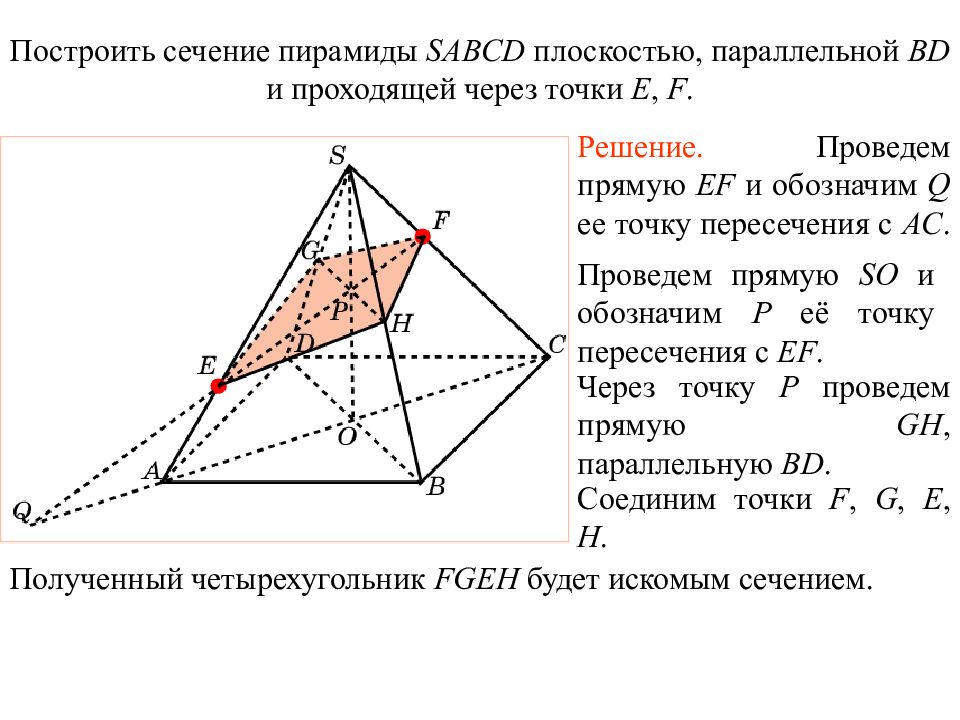
Слайд 35: Упражнение 2 1
Построить сечение пирамиды SABCD плоскостью, параллельной BD и проходящей через точки E, F. Решение. Проведем прямую EF и обозначим Q ее точку пересечения с AC. Проведем прямую SO и обозначим P её точку пересечения с EF. Через точку P проведем прямую GH, параллельную BD. Соединим точки F, G, E, H. Полученный четырехугольник FGEH будет искомым сечением. Упражнение 2 1
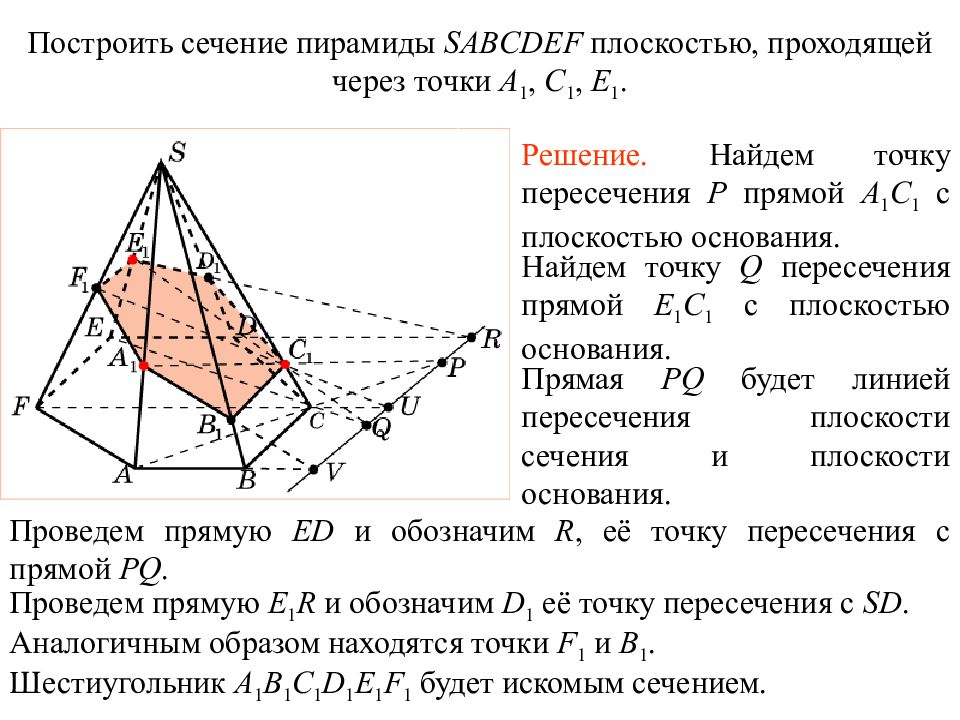
Последний слайд презентации: СЕЧЕНИЯ МНОГОГРАННИКОВ: Упражнение 2 2
Решение. Найдем точку пересечения P прямой A 1 C 1 с плоскостью основания. Найдем точку Q пересечения прямой E 1 C 1 с плоскостью основания. Проведем прямую ED и обозначим R, её точку пересечения с прямой PQ. Прямая PQ будет линией пересечения плоскости сечения и плоскости основания. Построить сечение пирамиды SABCDEF плоскостью, проходящей через точки A 1, C 1, E 1. Аналогичным образом находятся точки F 1 и B 1. Проведем прямую E 1 R и обозначим D 1 её точку пересечения с SD. Шестиугольник A 1 B 1 C 1 D 1 E 1 F 1 будет искомым сечением. Упражнение 2 2