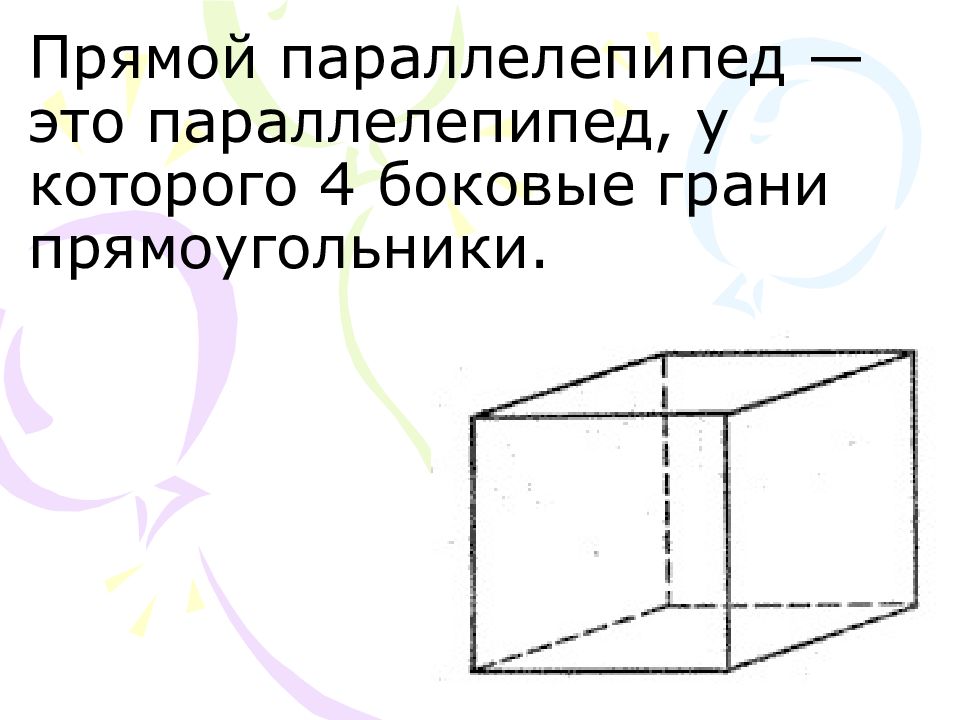
Слайд 3
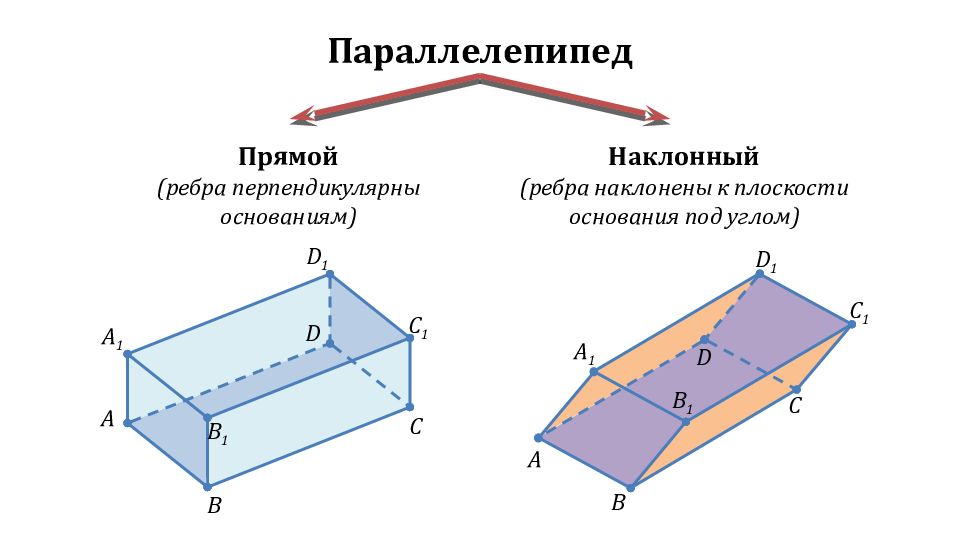
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Слайд 4
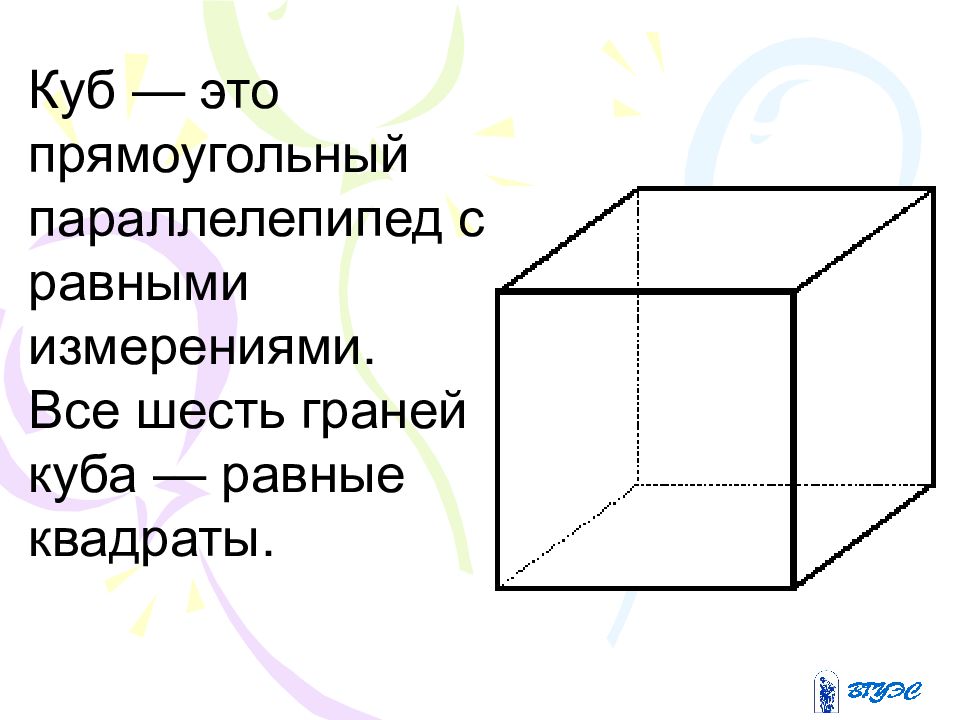
Куб — это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты.
Слайд 5: Свойства
- Параллелепипед симметричен относительно середины его диагонали. - Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
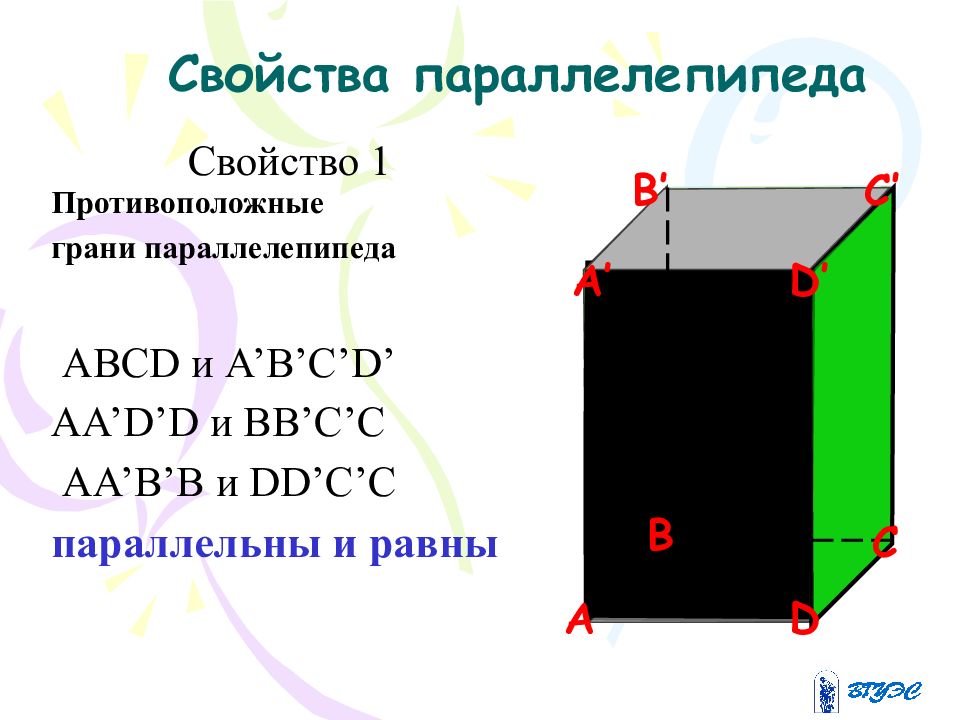
Слайд 6: Свойства параллелепипеда
Свойство 1 Противоположные грани параллелепипеда АВС D и А ’ В ’ С ’D’ АА ’D’D и ВВ ’ С ’ С АА ’ В ’ В и DD’ С ’ С параллельны и равны B’ C A D D’ A’ C’ B
Слайд 7
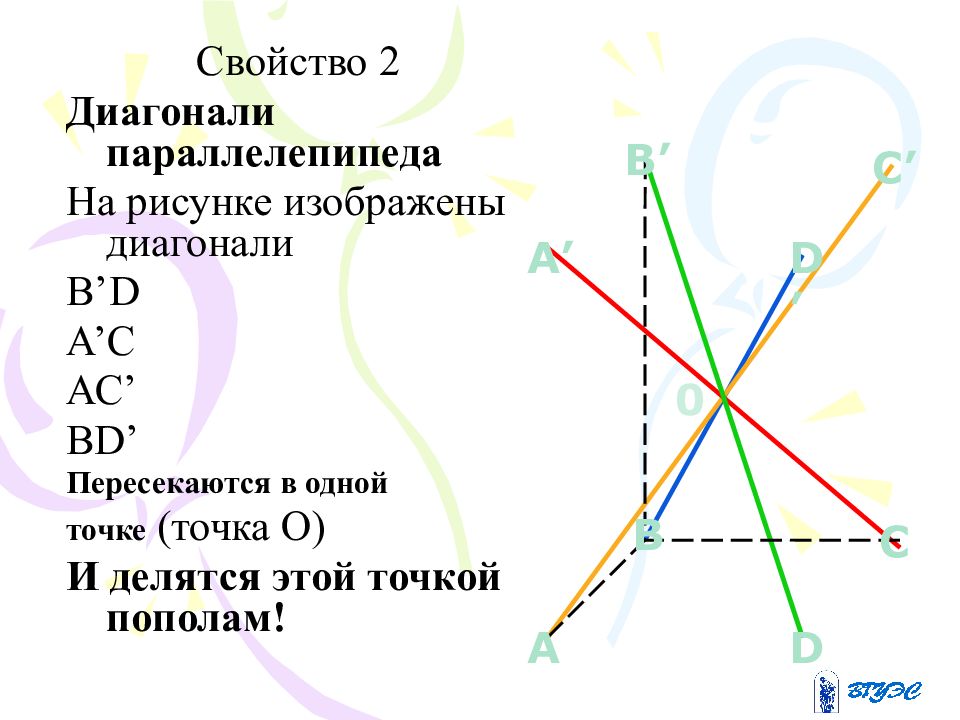
Свойство 2 Диагонали параллелепипеда На рисунке изображены диагонали В ’D А ’ С АС ’ В D’ Пересекаются в одной точке (точка О) И делятся этой точкой пополам! B C A D D’ A’ C’ B’ 0
Слайд 8
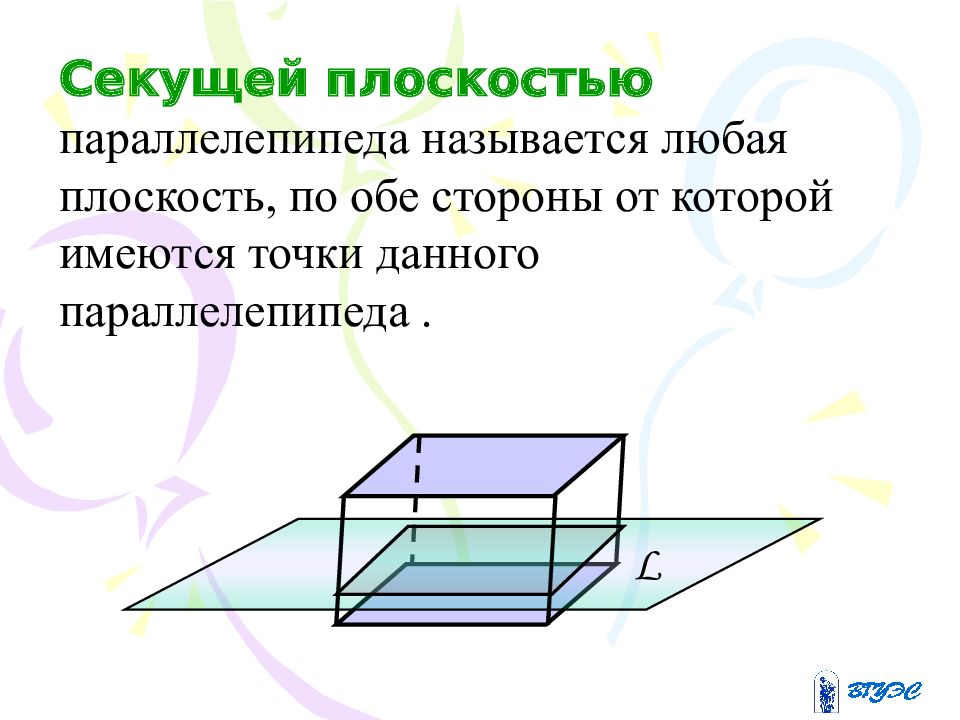
Секущей плоскостью параллелепипеда называется любая плоскость, по обе стороны от которой имеются точки данного параллелепипеда. L
Слайд 9
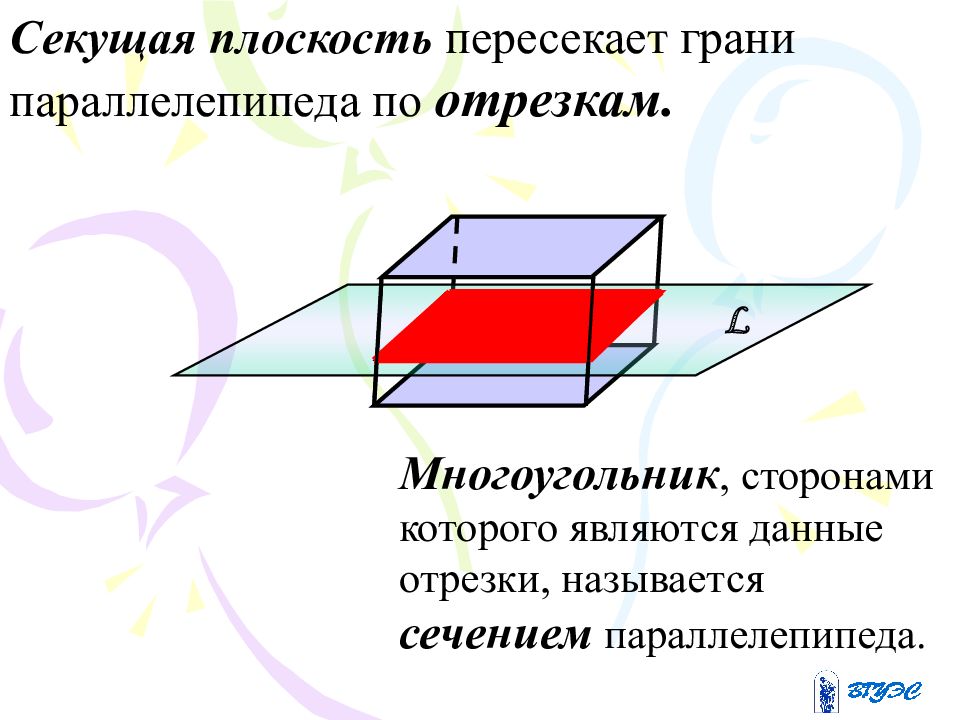
Секущая плоскость пересекает грани параллелепипеда по отрезкам. Многоугольник, сторонами которого являются данные отрезки, называется сечением параллелепипеда. L
Слайд 10: При этом необходимо учитывать следующее:
1. Соединять можно только две точки, лежащие в плоскости одной грани. 2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам. 3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях. Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.
Слайд 11
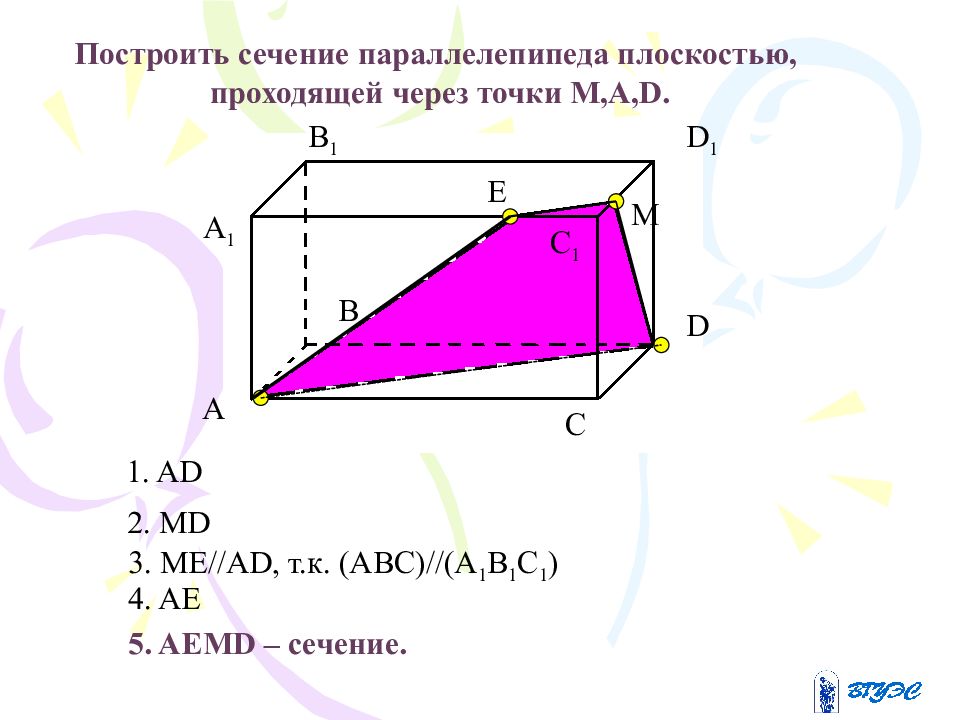
A 1 А В В 1 С С 1 D D 1 Построить сечение параллелепипеда плоскостью, проходящей через точки M,A,D. М 1. AD 2. MD 3. ME//AD, т.к. ( ABC)//(A 1 B 1 C 1 ) 4. AE 5. AEMD – сечение. E
Слайд 12
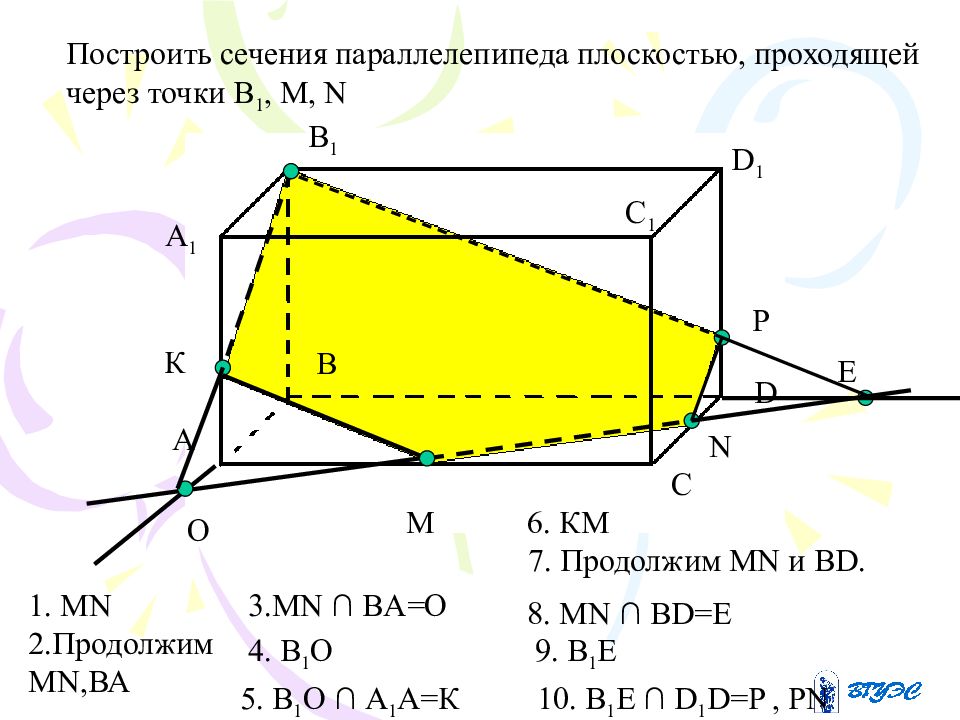
A 1 А В В 1 С С 1 D D 1 M N Построить сечения параллелепипеда плоскостью, проходящей через точки В 1, М, N O К Е P 1. MN 2.Продолжим MN,ВА 4. В 1 О 6. КМ 7. Продолжим MN и BD. 9. В 1 E 5. В 1 О ∩ А 1 А=К 8. MN ∩ BD=E 10. B 1 Е ∩ D 1 D=P, PN 3. MN ∩ BA=O
Слайд 13
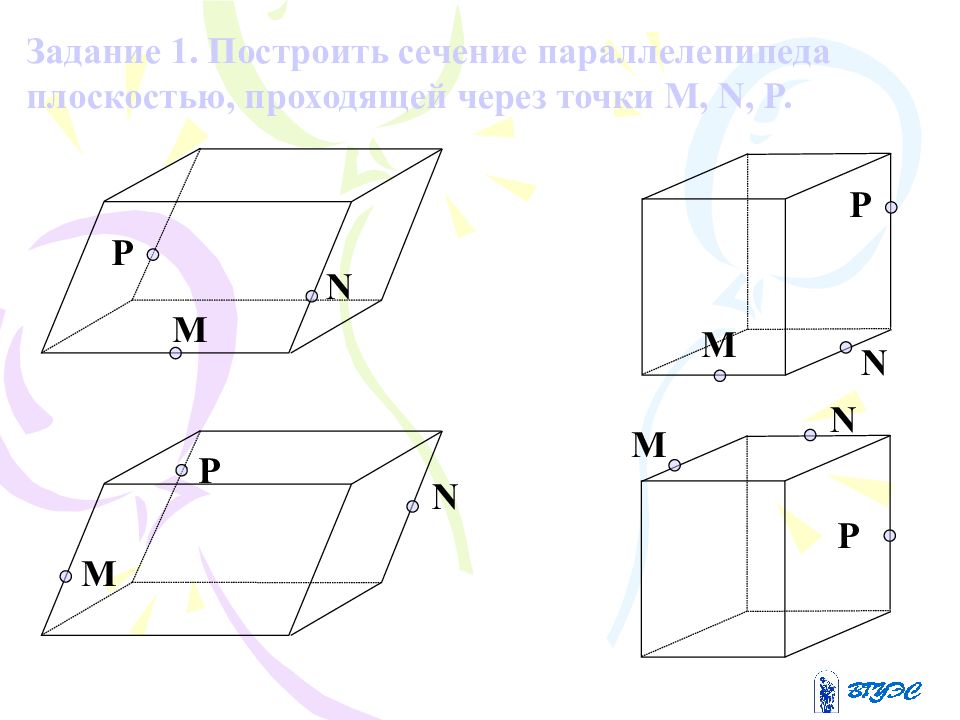
M N P M N P M N P M N P Задание 1. Построить сечение параллелепипеда плоскостью, проходящей через точки M, N, P.
Последний слайд презентации: ПАРАЛЛЕЛЕПИПЕД. СЕЧЕНИЕ ПАРАЛЛЕЛЕИППЕДА: Основные формулы
Прямой параллелепипед Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания Объём V=Sо*h Прямоугольный параллелепипед Основная статья : Прямоугольный параллелепипед Площадь боковой поверхности Sб =2c( a+b ), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда Площадь полной поверхности Sп =2( ab+bc+ac ) Объём V= abc, где a, b, c — измерения прямоугольного параллелепипеда. Куб Площадь боковой поверхности Sб =4a², где а — ребро куба Площадь полной поверхности Sп =6a² Объём V=a³