1) Понятия: система, совокупность. Содержание. 2) Алгоритмы решения систем и совокупностей уравнений и неравенств с одной переменной. 3) Тренировочные упражнения с пошаговым разбором. В ресурсе сделан акцент на использование понятий система – совокупность и правильное применение математической символики на примерах систем (совокупностей), содержащих квадратные уравнения и рациональные неравенства, подробное решение которых не предоставлено. При необходимости повтори: решение квадратных уравнений: решение линейных неравенств: решение рациональных неравенств: http://ta-shah.ucoz.ru/load/8_klass/8_klass/reshenie_linejnykh_neravenstv/10-1-0-62 http://ta-shah.ucoz.ru/load/8_klass/8_klass/reshenie_kvadratnykh_uravnenij_10_sposobov/10-1-0-30 http://ta-shah.ucoz.ru/load/egeh/egeh_s3/s3_1_reshenie_racionalnykh_neravenstv_metodom_intervalov/15-1-0-85
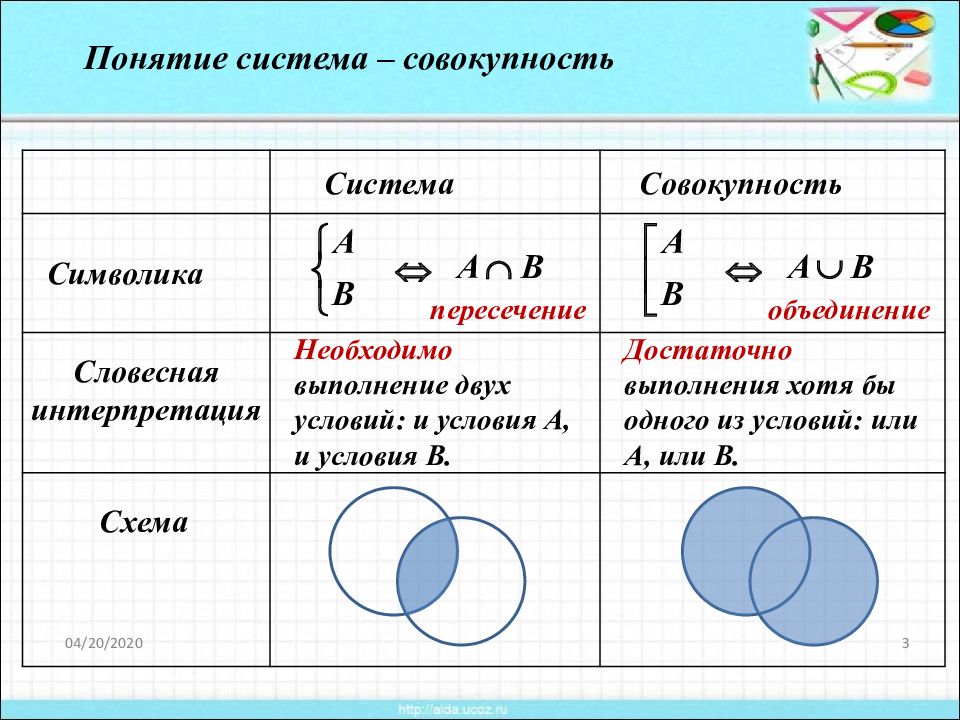
20.04.2020 3 Понятие система – совокупность Система Совокупность Символика Словесная интерпретация Схема Необходимо выполнение двух условий: и условия А, и условия В. Достаточно выполнения хотя бы одного из условий: или А, или В. пересечение объединение
20.04.2020 4 Понятие система – совокупность присутствует в решении квадратного уравнения по теореме Виета Необходимо выполнение двух условий: и первого, и второго – система. Для обращения уравнения в верное равенство достаточно выполнения хотя бы одного из условий: или первого, или второго – совокупность.
20.04.2020 5 Система Совокупность Решение системы уравнений с одной переменной. Решение совокупности уравнений с одной переменной. 1) Решить каждое уравнение независимо одно от другого. 2) В ответ записать общие решения данных уравнений. 1) Решить каждое уравнение независимо одно от другого. 2) В ответ записать все решения данных уравнений.
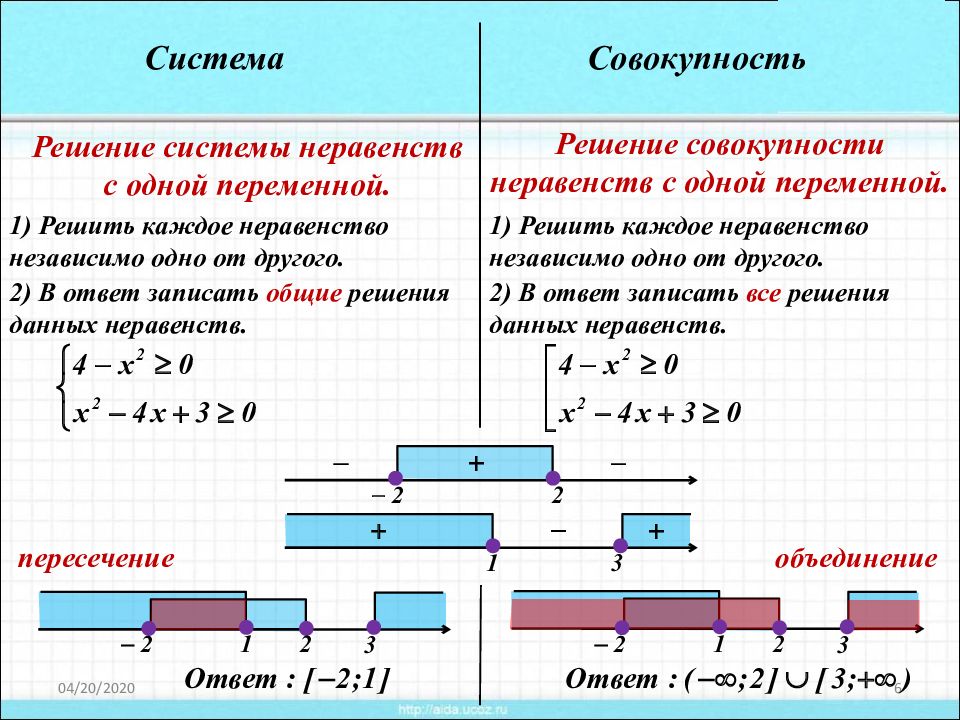
20.04.2020 6 Система Совокупность Решение системы неравенств с одной переменной. Решение совокупности неравенств с одной переменной. 1) Решить каждое неравенство независимо одно от другого. 2) В ответ записать общие решения данных неравенств. 1) Решить каждое неравенство независимо одно от другого. 2) В ответ записать все решения данных неравенств. пересечение объединение
20.04.2020 7 1. Решите уравнение: Некоторые задачи, при решении которых возникает понятие система – совокупность. Так как квадрат принимает только неотрицательные значения, то рассматриваемая сумма может быть равна нулю только в случае, если и то и другое слагаемое принимают значение ноль (система).
20.04.2020 8 2. Решите уравнение: Некоторые задачи, при решении которых возникает понятие система – совокупность. Произведение равно нулю, если хотя бы один множитель равен нулю, или первый, или второй (совокупность).
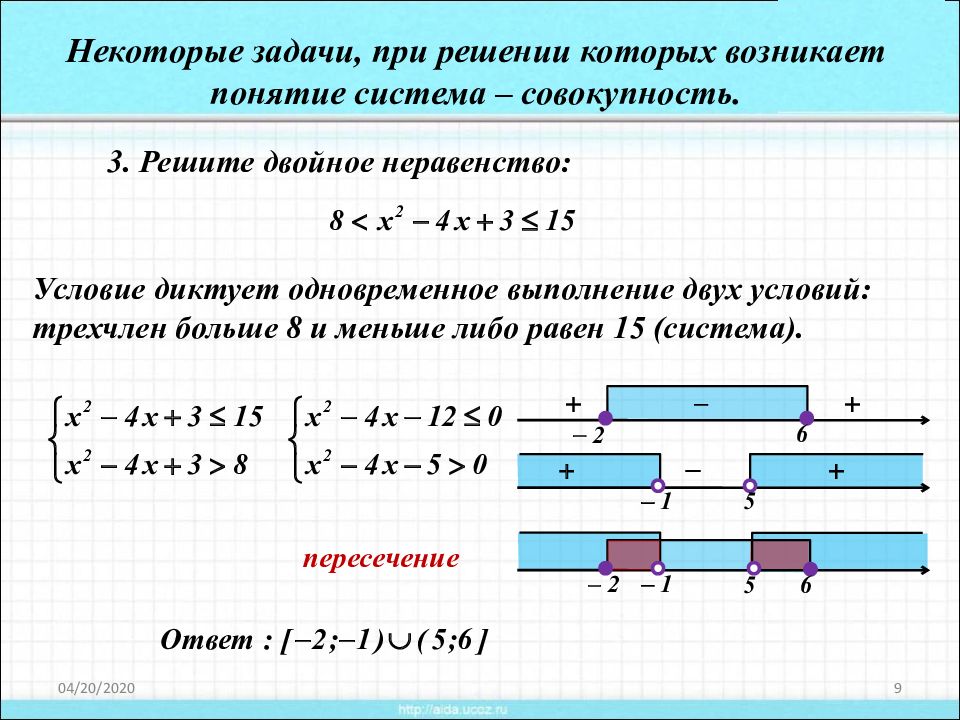
20.04.2020 9 3. Решите двойное неравенство: Некоторые задачи, при решении которых возникает понятие система – совокупность. Условие диктует одновременное выполнение двух условий: трехчлен больше 8 и меньше либо равен 15 (система). пересечение
20.04.2020 4. Решите неравенство методом замены переменной: Некоторые задачи, при решении которых возникает понятие система – совокупность. - совокупность. объединение
20.04.2020 5. Решите неравенство методом замены переменной: Некоторые задачи, при решении которых возникает понятие система – совокупность. - система Ø пересечение
20.04.2020 6. Найдите область определения функции. Некоторые задачи, при решении которых возникает понятие система – совокупность. пересечение Условие существования квадратного корня: Условие существования дроби:
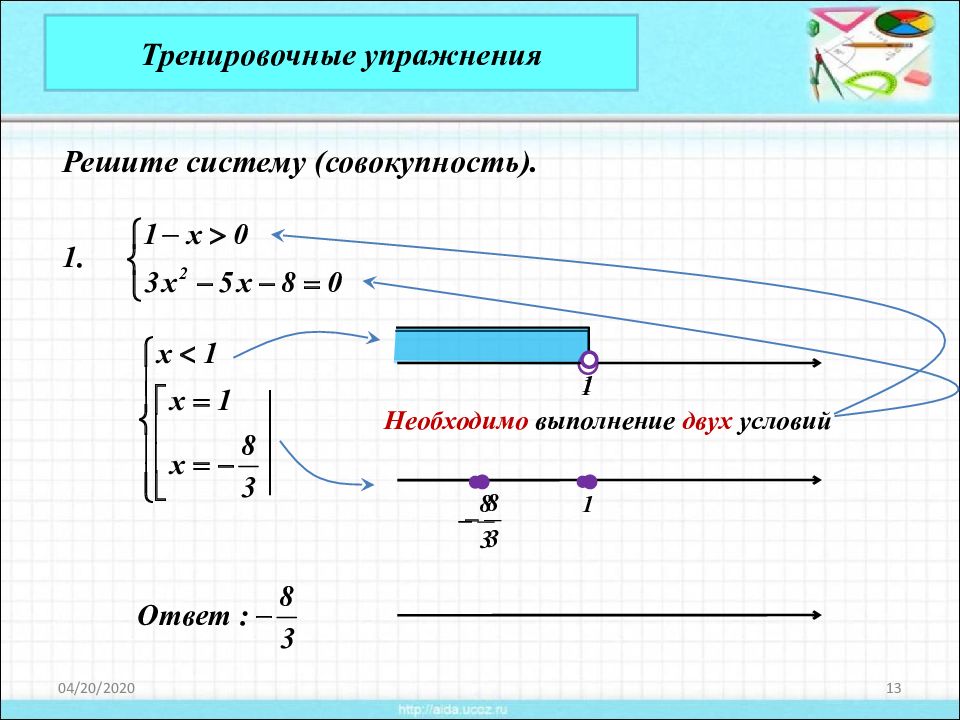
20.04.2020 13 Тренировочные упражнения Решите систему (совокупность). Необходимо выполнение двух условий
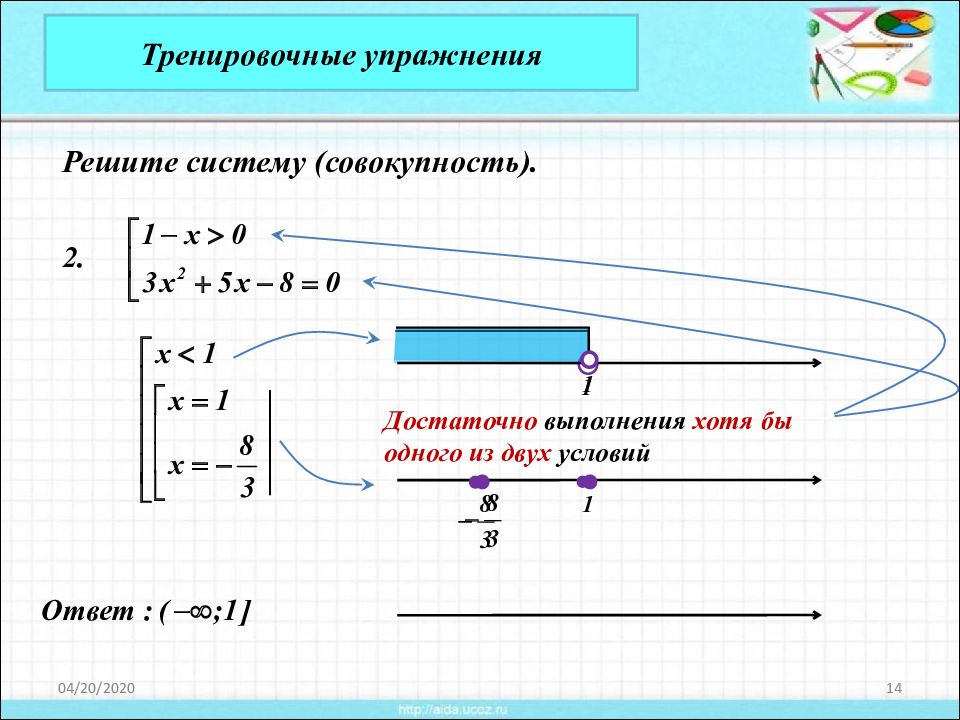
20.04.2020 14 Тренировочные упражнения Решите систему (совокупность). Достаточно выполнения хотя бы одного из двух условий
20.04.2020 15 Замечание. В случае, если вы не уверены в том, что правильно используете знак «система», «совокупность», то лучше этого избежать. На экзамене за неверное использование математической символики может быть снижен балл. Однако, в литературе и в различных ресурсах интернета эта символика используется очень часто. Например, при решении неравенств с модулями с использованием альтернативных переходов. Поэтому полезно все - же ориентироваться в данных понятиях. Как можно записать начало решения, например, иррационального уравнения (экзамен)? ОДЗ : Условие существования корней: Возведем обе части в квадрат: Условно. (на самом деле даже при выполнении этого условия корней может не быть) Все записи верны.
Спасибо за внимание. В следующих ресурсах рассмотренные понятия и символы будут использоваться.
