Первый слайд презентации: СТАТИСТИКА И ТЕОРИЯ ВЕРОЯТНОСТЕЙ 9 класс
Испытание. Успех и неудача. Серия испытаний до первого успеха 1
Слайд 2: СОБЫТИЯ
Случайное событие - событие называется случайным, если нельзя утверждать, что это событие в данных обстоятельствах произойдет. Элементарное событие – Вероятность – Частота случайного события – Маловероятное случайное событие – Равновероятные события – Достоверное событие – Невозможное событие – Наибольшее и наименьшее значение вероятности – Несовместные события – Независимые события -
Слайд 3: Испытание Бернулли
Определение. Испытанием Бернулли называют случайный опыт, который может закончиться одним из двух элементарных событий.
Слайд 4: УСПЕХ И НЕУДАЧА
Одно из двух элементарных событий в таких опытах условно называют успехом, а другой — неудачей. Вероятность того, что опыт закончится успехом, обычно обозначают буквой р. Вероятность неудачи обозначают q. Числа р и q положительные, при этом p + q = 1.
Если проводится несколько одинаковых и независимых испытаний Бернулли подряд, то говорят, что проведена серия или последовательность испытаний Бернулли. Серия испытаний Бернулли также является случайным экспериментом.
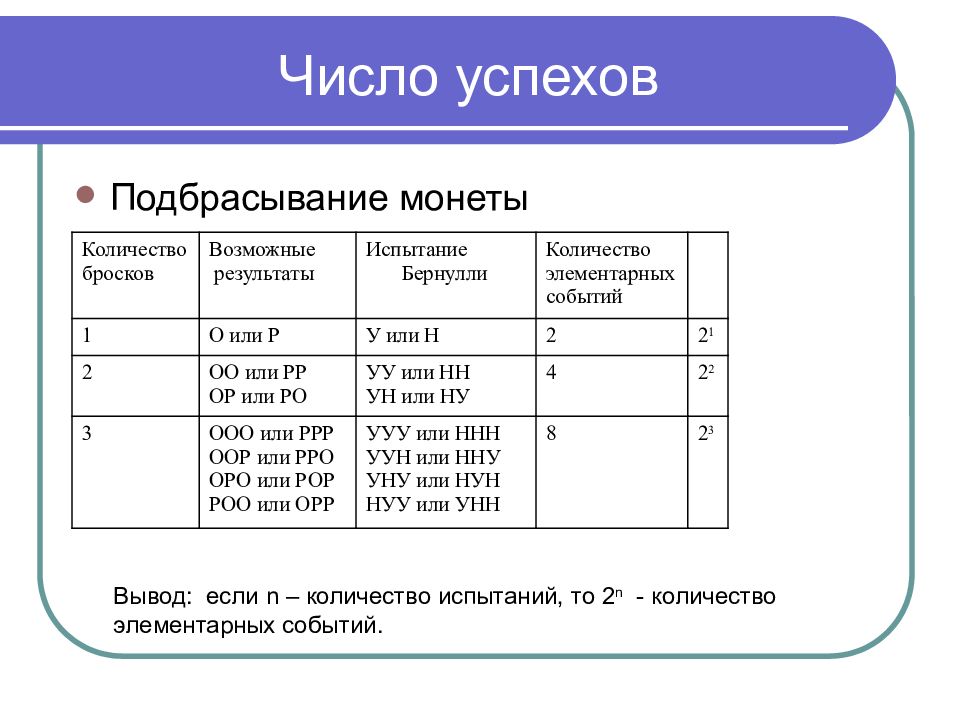
Слайд 6: Число успехов
Подбрасывание монеты Вывод: если n – количество испытаний, то 2 n - количество элементарных событий. Количество бросков Возможные результаты Испытание Бернулли Количество элементарных событий 1 О или Р У или Н 2 2 1 2 ОО или РР ОР или РО УУ или НН УН или НУ 4 2 2 3 ООО или РРР ООР или РРО ОРО или РОР РОО или ОРР УУУ или ННН УУН или ННУ УНУ или НУН НУУ или УНН 8 2 3
Слайд 7: Вероятность успеха
При одном подбрасывании монеты вероятность выпадения орла ( О или Р - У или Н) При двух подбрасываниях монеты вероятность события -выпадение орла при каждом броске (ОО, то есть УУ)
Слайд 8: Вероятности событий
При проведении серии из n независимых испытаний Бернулли одно элементарное событие с k успехами имеет вероятность Число таких элементарных событий с k успехами равно событие «наступило ровно к успехов» имеет вероятность
Слайд 9: Пример 1
При стрельбе в мишень с вероятностью попадания производится 7 выстрелов. Какова вероятность попасть в мишень ровно 3 раза? Решение. n=7, k=3, p=, q=1- = Выполним расчеты по формуле вероятностей , где