Классификация элементов систем Уравнения динамики и статики. Понятие передаточной функции Передаточные функции различных соединений звеньев Временные характеристики систем и их элементов
Система автоматического управления – это совокупность элементов, соединенных в замкнутый контур, которые функционируют согласованно и подчинены определенной форме управления. По функциональному назначению: Измерительные Усилительно-преобразовательные Исполнительные Корректирующие
По виду энергии, используемой для работы: Электрические Механические Гидравлические Пневматические Комбинированные По характеру математического соответствия между входным и выходным сигналами.
При математическом описании элементы называются звеньями САУ. Несмотря на многообразие различного рода элементов (устройств) и независимо от физических принципов их работы, поведение каждого из них может быть описано дифференциальным уравнением, связывающим входную и выходную переменные. Элементы описываются, как правило, дифференциальными уравнениями первого или второго порядка. Рассматриваем одномерную модель с одним входом и одним выходом, и обозначим входную величину звена через u ( t ), а выходную через y ( t ). При рассмотрении линейных систем статическая характеристика y = f ( t ) любого звена может быть изображена прямой линией.
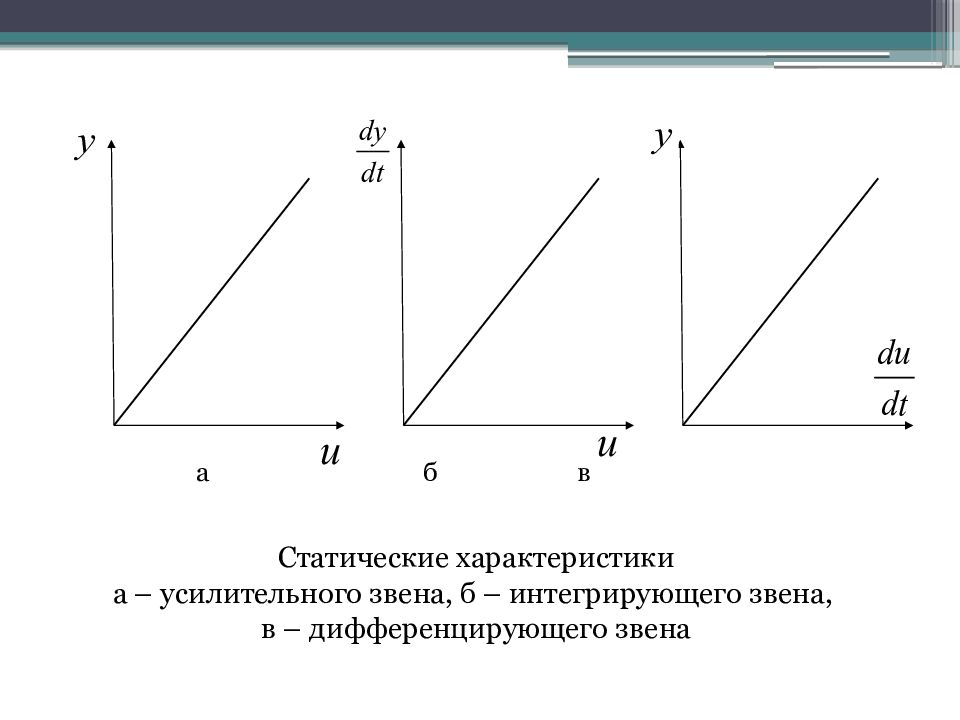
В позиционном (или усилительном) звене линейной зависимостью y = Ku связаны входная и выходная величина в установившемся режиме. K - коэффициент передачи или коэффициент усиления звена. В интегрирующих звеньях линейной зависимостью связаны производная выходной величины и входная величина в установившемся режиме. В дифференцирующих звеньях линейной зависимостью связаны в установившемся режиме выходная величина и производная входной величины
a б в Статические характеристики а – усилительного звена, б – интегрирующего звена, в – дифференцирующего звена
В общем случае линейная система описывается линейным дифференциальным уравнением, представленным в стандартной форме где t – текущее время; n – порядок дифференциального уравнения; m ≥ n u – входное воздействие (сигнал); y- выходное воздействие(сигнал); a i и b j - коэффициенты, определяемые параметрами системы. Если эти коэффициенты не зависят от времени, то система называется стационарной. (1)
Дифференциальные уравнения называют уравнениями динамики, они описывают переходные режимы в системах. Переходной режим возникает при подаче на вход сигнала (включение устройства) и существует до тех пор, пока на выходе не устанавливается определенная величина сигнала. Переходной процесс – это процесс изменения сигнала y ( t ) на выходе от момента подачи входного сигнала u ( t ) до установления процесса на выходе. С математической точки зрения y ( t ) – решение дифференциального уравнения. Уравнение статики – уравнение установившегося режима, когда все производные равны нулю.
В инженерной практике широко используется метод решения дифференциальных уравнений, основанный на интегральном преобразовании Лапласа и позволяющий свести задачу к алгебраическим действиям. Для сигнала f ( t ) преобразование Лапласа где s – оператор Лапласа F ( s ) - называется изображением функции f ( t )
y ( t ) – оригинал ; Y ( s ) – изображение функции y ( t ); s – комплексная переменная; х ( t ) ( t > 0) Х ( s ) = L [ х ( t )] 1(t) 1/s δ ( t) 1 t 1/s 2 t n n!/s n+1 e at 1/(s – a) e -at 1/(s + a) t·e at 1/(s – a) 2 t n ·e at n!/(s – a) n+1 sin( ωt ) ω/(s 2 + ω 2 ) cos(ωt) s/(s 2 + ω 2 ) Соответствие между рядом оригиналов и изображений
При нулевых начальных условиях, т. е. в том случае, если при t < 0 (до момента подачи сигнала) входная и выходная величины, а так же их производные, тождественно равны нулю, o т уравнения (1) формально можно перейти к выражению: (2) Передаточная функция звена (системы) W(s) – это отношение изображения по Лапласу выходного сигнала Y(s) к изображению по Лапласу входного сигнала U(s) при нулевых начальных условиях
Примем Прямое преобразование Лапласа
Передаточные функции звеньев имеют вид: - Позиционное или усилительное звено Интегрирующее звено Дифференцирующее звено Передаточная функция – это одна из форм математических моделей элементов. =
Передаточная функция элемента не зависит от того, какой функцией времени является его входное воздействие. Она зависит лишь от вида дифференциального уравнения и от значений параметров элемента, которые определяют коэффициенты уравнения. Зная W(s) и U(S) можно найти Y(s) – изображение по Лапласу выходного сигнала: Y(s)= W(s)*U(S), тогда можно найти как обратное преобразование Лапласа:
W ( s ) можно представить следующим образом: где K – коэффициент усиления, – нули системы, т. е. корни многочлена числителя, – полюсы системы, т. е. корни многочлена знаменателя.
Для описания моделей систем и действий над ними широко используется система MATLAB и пакет прикладных программ Control System Toolbox. В пакете введен класс объектов, называемый lti объекты – линейные с постоянными параметрами. При создании lti объекта ему присваивается имя. - tf - форма, передаточная функция задается двумя векторами строками, составленными из коэффициентов многочленов числителя и знаменателя в порядке убывания степеней s. Например, оператор W = tf ([2 1], [1 3 7]) создает объект W подкласса tf, соответствующий передаточной функции =
zpk- форма нулей, полюсов и коэффициента усиления, в которой передаточная функция описывается двумя векторами-строками и одним числом, задающим нули, полюсы и коэффициент усиления системы. Например: = При отсутствии нулей на их место записывается знак пусто []. ss -форма представляет передаточную функцию в параметрах пространства состояний.
При описании элементов и систем кроме входных u ( t ) и выходных y ( t ) переменных можно выделить некоторые промежуточные переменные x ( t ), которые связаны с внутренней структурой системы и называются переменными состояния. В параметрах пространства состояний система n -го порядка с одним входом и одним выходом описывается системой уравнений где A – квадратная матрица порядка n, элементы которой определяются коэффициентами дифференциального уравнения, B – вектор-столбец [n·1] постоянных коэффициентов, C – вектор-строка [1·n] постоянных коэффициентов, D – одноэлементная матрица.
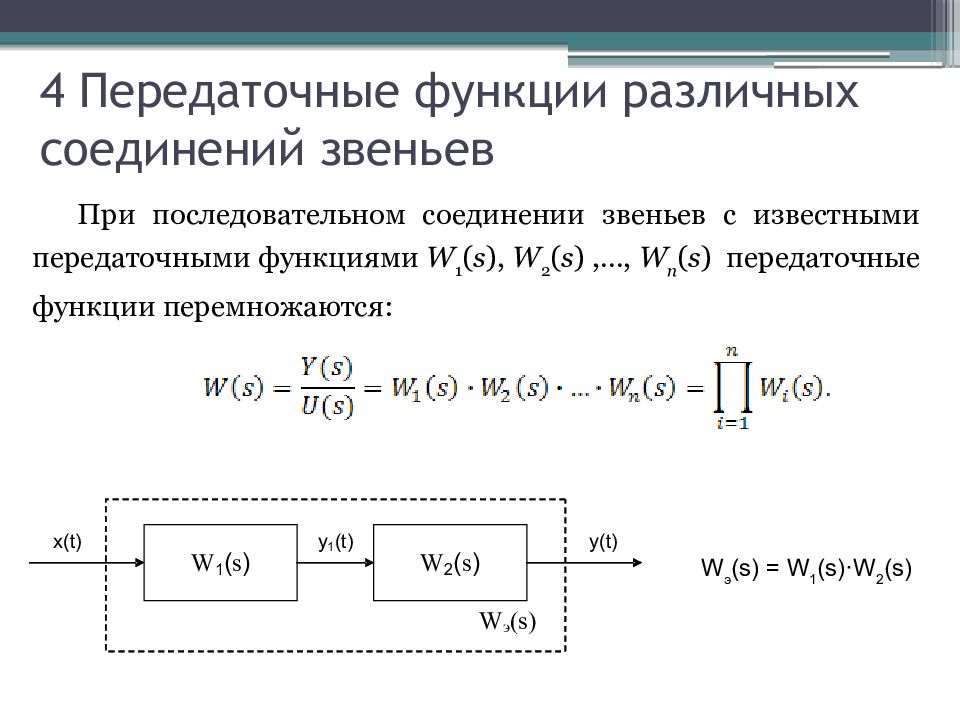
При последовательном соединении звеньев с известными передаточными функциями W 1 ( s ), W 2 ( s ) ,…, W n ( s ) передаточные функции перемножаются: W э (s) = W 1 (s)·W 2 (s)
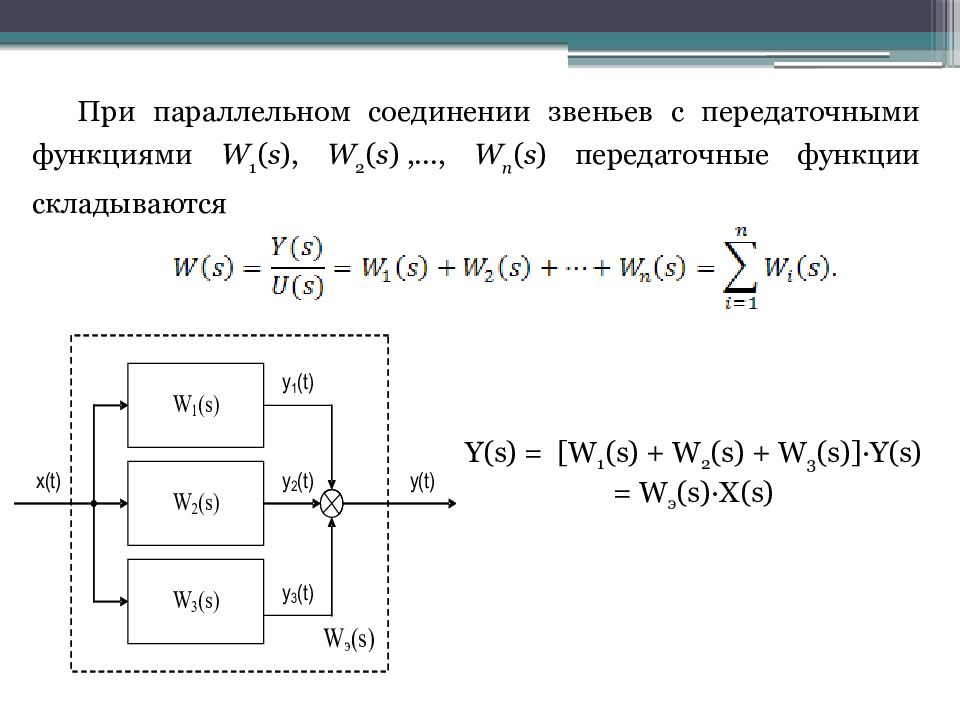
При параллельном соединении звеньев с передаточными функциями W 1 ( s ), W 2 ( s ) ,…, W n ( s ) передаточные функции складываются Y(s) = [W 1 (s) + W 2 (s) + W 3 (s)]·Y(s) = W э (s)·X(s)
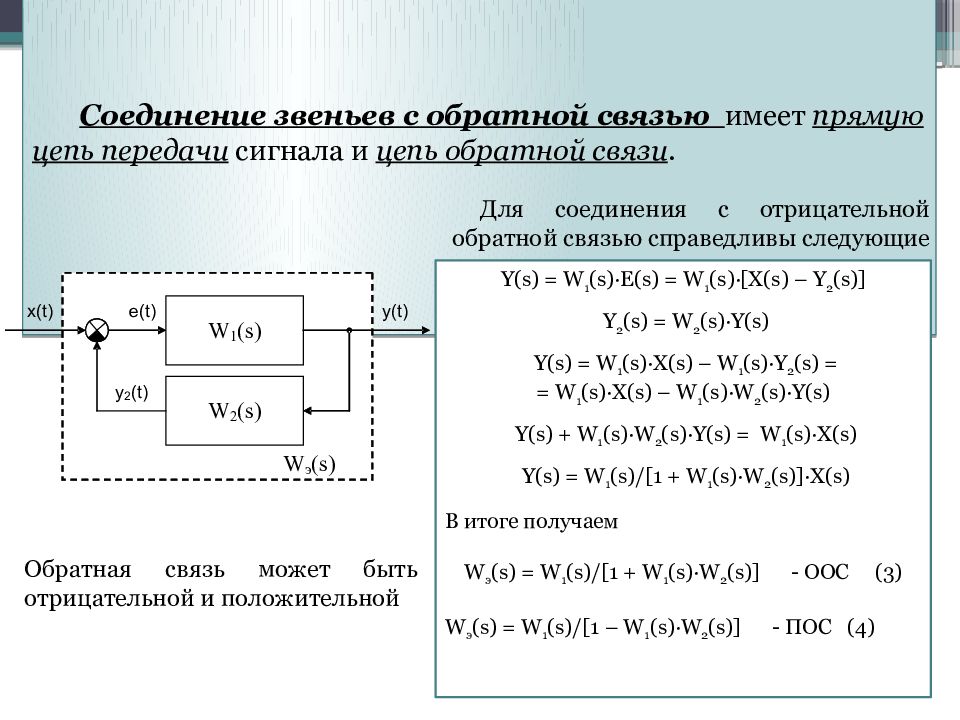
Соединение звеньев с обратной связью имеет прямую цепь передачи сигнала и цепь обратной связи. Для соединения с отрицательной обратной связью справедливы следующие соотношения: Y(s) = W 1 (s)·E(s) = W 1 (s)·[X(s) – Y 2 (s)] Y 2 (s) = W 2 (s)·Y(s) Y(s) = W 1 (s)·X(s) – W 1 (s)·Y 2 (s) = = W 1 (s)·X(s) – W 1 (s)·W 2 (s)·Y(s) Y(s) + W 1 (s)·W 2 (s)·Y(s) = W 1 (s)·X(s) Y(s) = W 1 (s)/[1 + W 1 (s)·W 2 (s)]·X(s) В итоге получаем W э ( s ) = W 1 ( s )/[1 + W 1 ( s )· W 2 ( s )] - ООС (3) W э ( s ) = W 1 ( s )/[1 – W 1 ( s )· W 2 ( s )] - ПОС (4) Обратная связь может быть отрицательной и положительной
Типовые воздействия Единичное ступенчатое воздействие Единичное импульсное воздействие, ( дельта – функция)
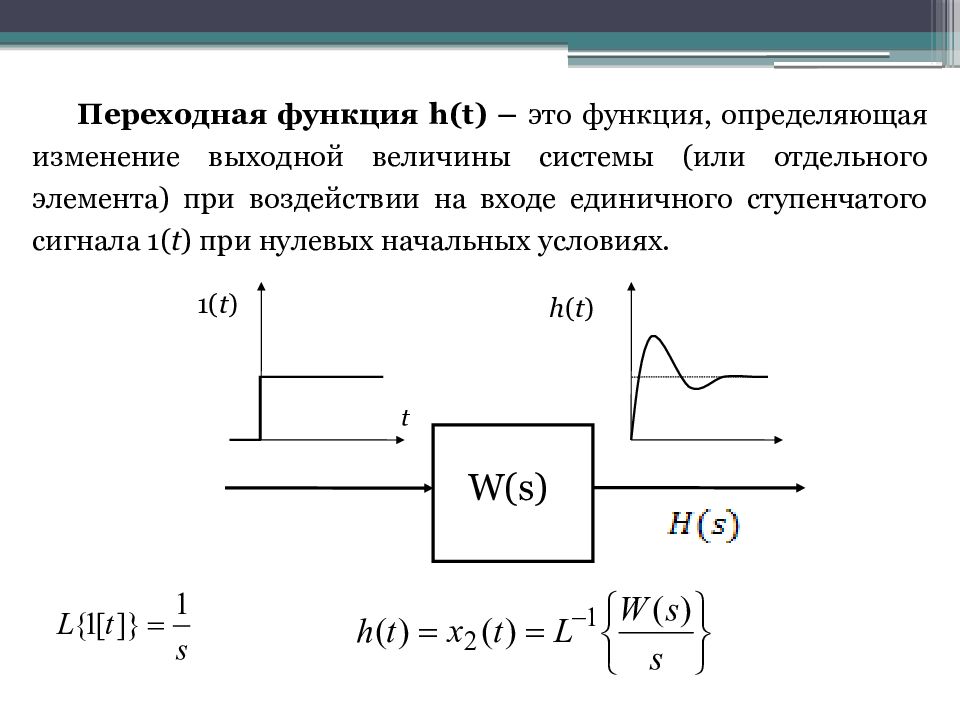
Переходная функция h(t) – это функция, определяющая изменение выходной величины системы (или отдельного элемента) при воздействии на входе единичного ступенчатого сигнала 1( t ) при нулевых начальных условиях. t 1( t ) h ( t ) W(s)
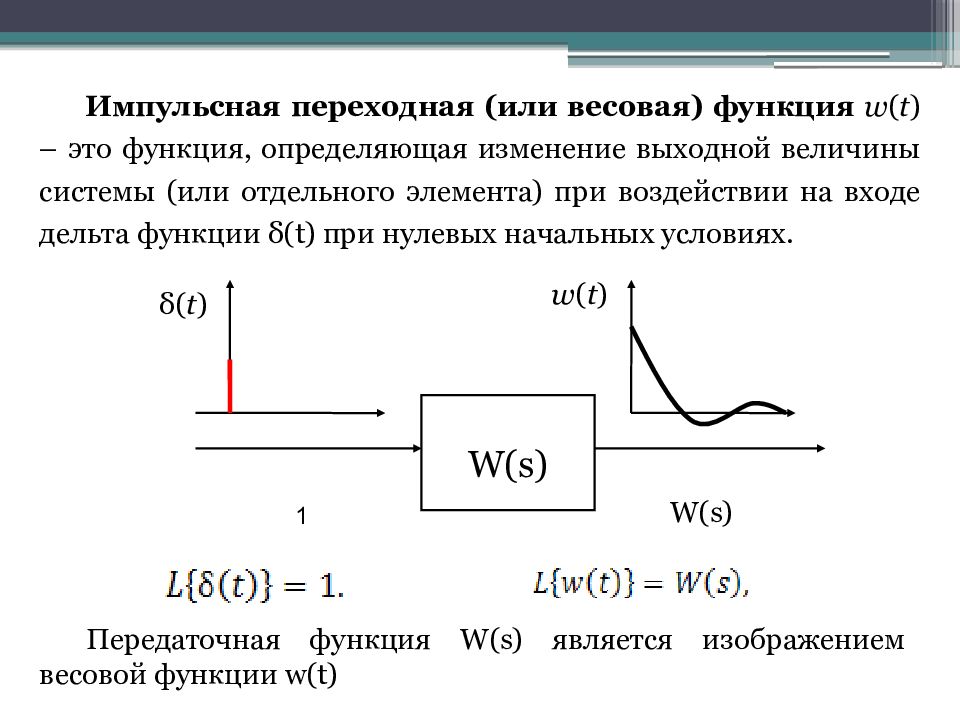
Импульсная переходная (или весовая) функция w ( t ) – это функция, определяющая изменение выходной величины системы (или отдельного элемента) при воздействии на входе дельта функции δ ( t ) при нулевых начальных условиях. δ( t ) w ( t ) W(s) 1 W(s) Передаточная функция W(s) является изображением весовой функции w(t)
Пример 1: Найти весовую функцию системы, если переходная функция равна Решение: Найдем изображение переходной функции Получаем передаточную функцию или изображение весовой функции Откуда весовая функция системы определяется по формуле
Пример 2. Определить передаточную, переходную и весовую функции звена, которое описывается дифференциальным уравнением Переходя в область изображений по Лапласу найдем передаточную функцию Решение:
Весовая или импульсная переходная характеристика: Переходная характеристика:
