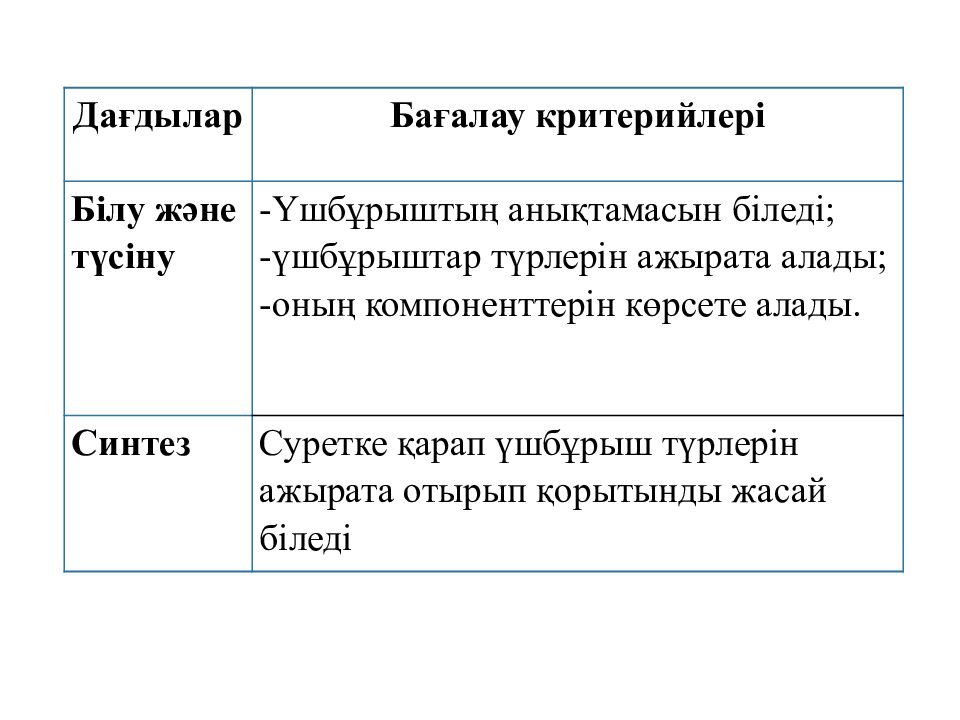
Дағдылар Бағалау критерийлері Білу және түсіну -Үшбұрыштың анықтамасын біледі; -үшбұрыштар түрлерін ажырата алады; -оның компоненттерін көрсете алады. Синтез Суретке қарап үшбұрыш түрлерін ажырата отырып қорытынды жасай біледі
№2.37. Табаны BC болатын ABC тең бүйірлі үшбұрышының AD медианасының бойынан E нүктесі алынған. Үшбұрыштардың теңдігін дәлелдеңдер: 1) △AEB және △AEC; №2.38. AB және CD кесінділері O нүктесінде қиылысады. Егер BO = CO және ∠ACO = ∠DBO болса, онда △ACO = △DBO теңдігін дәлелдеңдер. №2.39. AB және CD кесінділері O нүктесінде қиылысады. Егер AO = BO және ∠CAO = ∠DBO болса, онда △CAO = △DBO теңдігін дәлелдеңдер. №2.40. ABC үшбұрышында AB = BC, BD – биссектриса. Егер: 1) A төбесіндегі сыртқы бұрыш 130°-қа тең болса, онда ∠BCA бұрышын табыңдар; 2) егер AB = 5 см, AD = 2 см болса, онда ABC үшбұрышының периметрін табыңдар.
№2.28. Табаны BC болатын тең бүйірлі ABC үшбұрышында ∠B = 40°. C бұрышының сыртқы бұрышын табыңдар. №2.29. ON кесіндісі – AOB тік бұрышының биссектрисасы, ал OK және OP кесінділері – сәйкес AON және NOB бұрыштарының биссектрисалары. KOP бұрышын табыңдар (2.27-сурет). №2.30. A және C нүктелері a түзуіне қатысты әртүрлі жарты жазықтықтарда жатады және a түзуіне жүргізілген AB және CD перпендикулярлары тең. 1) ∆ABD = ∆CDB теңдігін дәлелдеңдер; 2) Егер ∠ADB = 44° болса, онда ∆ABC-ны табыңдар. №2.32. Тең бүйірлі үшбұрыштың табаны бүйір қабырғасынан екі есе кіші, ал периметрі 50 см. Үшбұрыштың қабырғаларын табыңдар. № 2.33. Табаны BC болатын тең бүйірлі ABC үшбұрышында ∠A = 40°. AC және BC қабырғаларын табыңдар
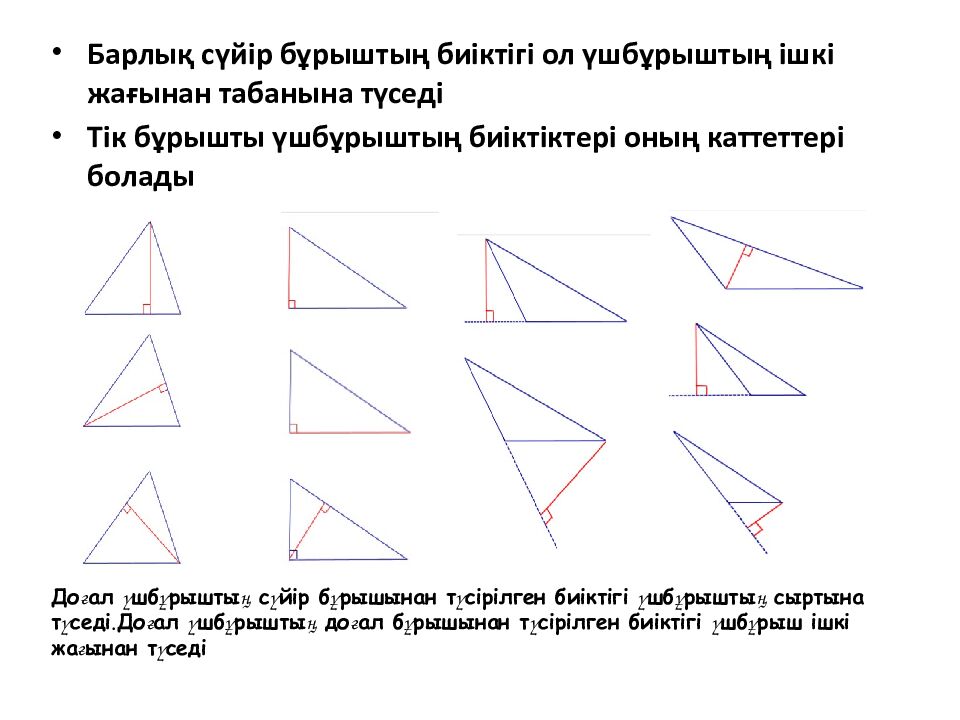
Барлық сүйір бұрыштың биіктігі ол үшбұрыштың ішкі жағынан табанына түседі Тік бұрышты үшбұрыштың биіктіктері оның каттеттері болады Доғал үшбұрыштың сүйір бұрышынан түсірілген биіктігі үшбұрыштың сыртына түседі. Доғал үшбұрыштың доғал бұрышынан түсірілген биіктігі үшбұрыш ішкі жағынан түседі
Рефлексия Сабаққа мен белсенді / белсенді емес қатынастым. Сабақтағы өз жұмысыма ризамын / әлі де жұмыстануым керек. Шығарылған есептер түсінікті болды / тағы да қарап шығуым керек.
