Упругие волны
Волны. Продольные и поперечные волны. Волной называется процесс распространения колебаний в пространстве с течением времени. Фронт волны - поверхность, которая отделяет часть пространства, вовлеченного в волновой процесс, от области, в которой колебания еще не возникли. Фронт волны (волновой фронт) - геометрическое место точек, которых достигла распространяющаяся в пространстве волна. Волновая поверхность - геометрическое место точек, которых в волне, совершающих колебания в одинаковой фазе.
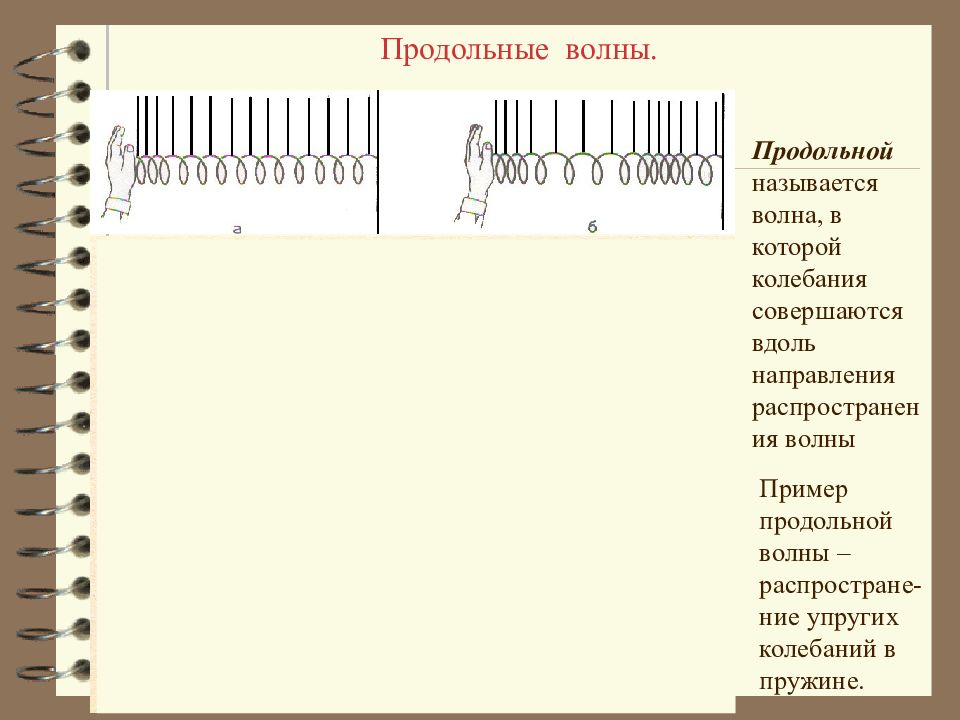
Продольные волны. Продольной называется волна, в которой колебания совершаются вдоль направления распространения волны Пример продольной волны – распростране-ние упругих колебаний в пружине.
Продольные волны. Распространение продольной волны в упругой среде.
Поперечные волны. Возбуждение продольной волны в упругой среде. На рисунке из старинного манускрипта показан древний народный способ возбуждения поперечной волны с помощью палки и верёвки. Поперечной называется волна, в которой колебания совершаются в направлении, перпендикулярном направлению распространения волны.
Поперечные волны. Процесс распространения поперечной волны. В момент времени t = 0 колебания отсутствуют. t = T/4, Т - период колебаний. t = T/ 2. t = 3 T/ 4. t = T. t = 5 T /4.
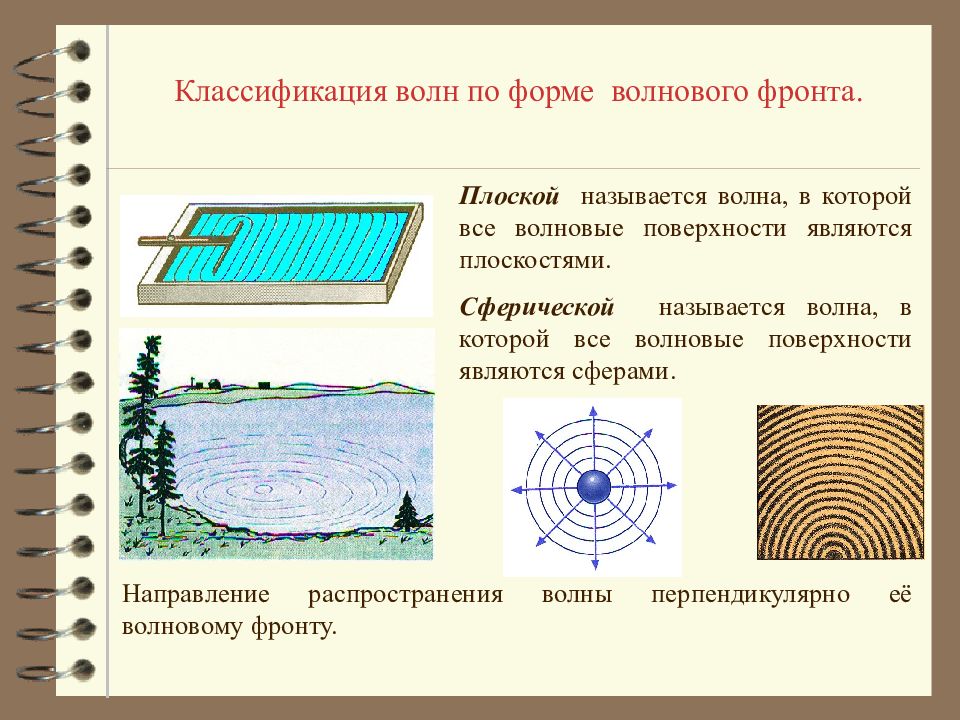
Классификация волн по форме волнового фронта. Плоской называется волна, в которой все волновые поверхности являются плоскостями. Сферической называется волна, в которой все волновые поверхности являются сферами. Направление распространения волны перпендикулярно её волновому фронту.
Уравнение плоской волны. Уравнение волны - выражение, которое задаёт смещение колеблющейся частицы, как функцию координат и времени: Рассмотрим процесс распространения плоской волны (безразлично, продольной или поперечной). Пусть c - скорость распространения волны (это не скорость движения частиц в волне v !). В момент времени t = 0 начинается распространение колебаний в пространстве. К моменту времени t = t достигнет точки x 1 ( см. рис.).
Пусть в плоскости x = 0 колебания происходят по закону Чтобы достичь точки с координатой x 1 = c t, волне потребуется время Следовательно, колебания в плоскости с координатой x = x 1, будут запаздывать по сравнению с колебаниями в плоскости с координатой x = 0 на время Подобное рассуждение справедливо для плоскости с любой координатой x. Поэтому уравнение колебаний частиц, в плоскости c координатой x можно записать так:
Это и есть уравнение плоской волны, распространяющейся вдоль положительного направления оси OX. Уравнение плоской волны, распространяющейся вдоль отрицательного направления оси OX : Здесь - циклическая частота колебаний, с - скорость распространения поверхности постоянной фазы (напр. волнового фронта) или фазовая волны, A - амплитуда колебаний в волне, - начальная фаза колебаний.
Волновое число. Волновой вектор. Перепишем уравнение плоской волны, распространяющейся вдоль положительного направления оси OX : Обозначим тогда Величина k называется волновым числом. Если плоская волна распространяется в произвольном направлении, не совпадающем с с направлением какой-либо из осей координат, то уравнение плоской волны можно записать так:
Волновое число. Волновой вектор. Здесь k называется волновым вектором,
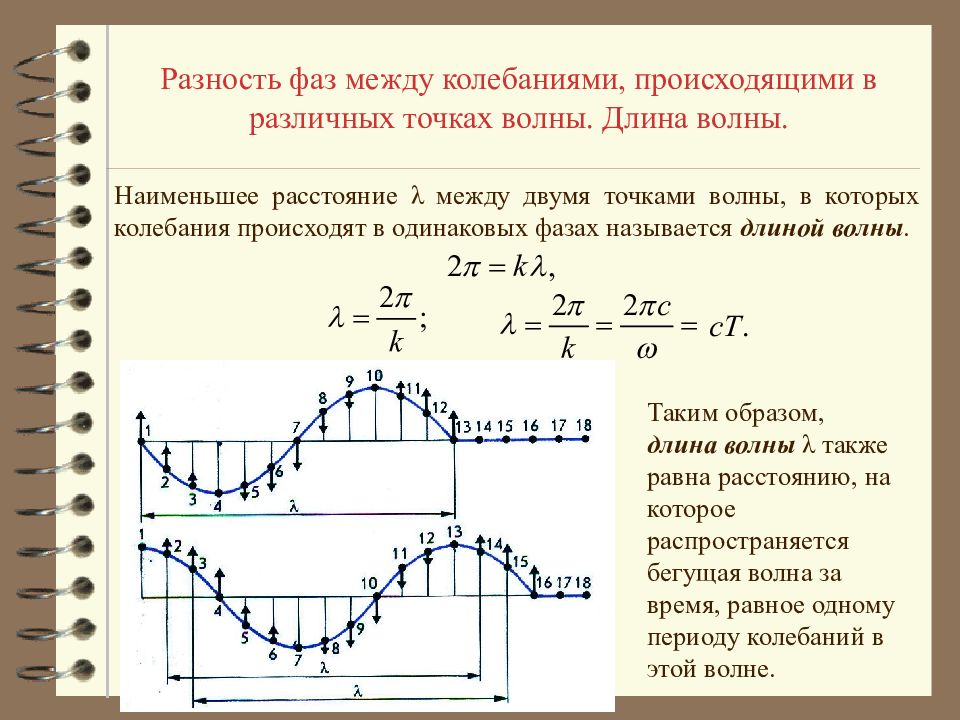
Разность фаз между колебаниями, происходящими в различных точках волны. Длина волны. Уравнение плоской волны, распространяющейся вдоль положительного направления оси OX Выражение в скобках называется фазой колебаний. Разность фаз между колебаниями в двух пространственных точках плоской волны L 12 – расстояние между двумя пространственными точками. Гармоническая функция имеет период, равный 2 π, поэтому наименьшее расстояние λ между двумя точками, в которых колебания происходят в одинаковых фазах определяется уравнением
Разность фаз между колебаниями, происходящими в различных точках волны. Длина волны. Наименьшее расстояние λ между двумя точками волны, в которых колебания происходят в одинаковых фазах называется длиной волны. Таким образом, длина волны λ также равна расстоянию, на которое распространяется бегущая волна за время, равное одному периоду колебаний в этой волне.
Фазовая скорость волны. Волновые поверхности - это геометрическое место точек, в которых колебания происходят в одинаковой фазе. Волновой фронт - одна из таких поверхностей. Поэтому, чтобы определить скорость распространения волны в пространстве, будем считать, что фаза постоянна, то есть = const. Найдём полный дифференциал d :
Фазовая скорость волны. Отсюда Таким образом, скорость распространения волны есть скорость перемещения поверхности постоянной фазы. Она ещё называется фазовой скоростью.
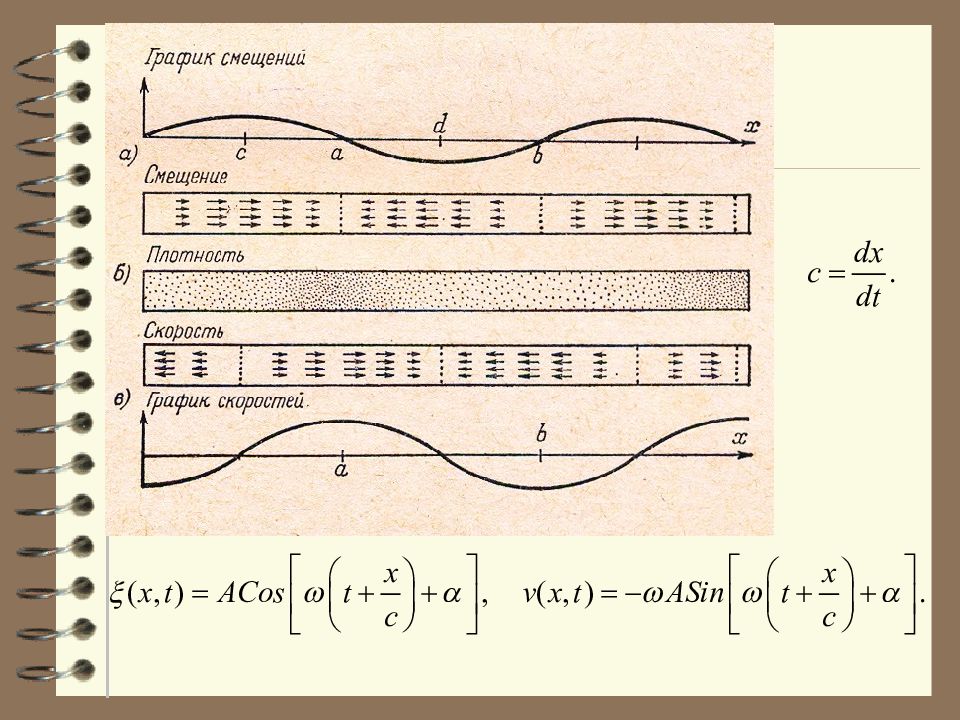
Колебания частиц среды в упругой поперечной и продольной волне. Скорость волны - это скорость распространения колебаний в пространстве : Скорость движения частиц упругой среды, участвующих в колебаниях можно найти так: Скорость распространения волны на рисунке обозначена буквой c Скорость движения частиц упругой среды - v.
Волновое уравнение. Уравнение волны есть решение некоторого дифференциального уравнения, описывающего движение частиц упругой среды. попытаемся подобрать вид дифференциального уравнения, решением которого было бы уравнение плоской волны. Дифференциальное уравнение должно описывать движение частиц среды, поэтому оно должно содержать производные по времени t и пространственным переменным x, y и z. При этом, если мы будем рассматривать процесс колебаний в некоторой фиксированной пространственной точке, то в каждой точке пространства, то есть при любых ( x,y,z ) это должно быт уравнение, описывающее гармонические колебания.
Волновое уравнение. Дифференциальное уравнение должно содержать также производные по пространственным переменным x, y и z. Оно должно иметь вид: Здесь - некоторый дифференциальный оператор, содержащий производные по x, y, и z ; a - константа. Так как решением этого уравнения является гармоническая функция (синус или косинус), производные по x, y и z должны быть чётного порядка. Например, первая производная синуса есть косинус и при подстановке решения в виде гармонической функции дифференциальное уравнение не обратится в тождество.
Волновое уравнение. Предположим, в состав дифференциального оператора входят вторые производные по координатам. Тогда
Волновое уравнение.
Волновое уравнение. – оператор Лапласа. с – скорость распространения волны. Это и есть волновое уравнение. Легко убедиться прямой подстановкой, что уравнение плоской волны является его решением.
