Первый слайд презентации: Волновая оптика. 1. Электромагнитные волны
Уравнения Максвелла и волновое уравнение. 1.1.
Слайд 2: Список литературы
1. И.В.Савельев. Курс общей физики, т.2, и т.3. 2. Н.Н.Заичкин. Лекции по общему курсу физики. ч. VI. Оптика. 3. Сборник вопросов, упражнений и задач по дисциплине «Физика», Часть 3. (№2616 - 3). 4. Методическое пособие к решению задач по курсу физики в системе РИТМ. Часть 3. (№3126 - 3). 5. Н.И.Калитеевский. Волновая оптика. 6. А.Н.Матвеев. Оптика.
Уравнения Максвелла и волновое уравнение. 1.1.
Слайд 4
1.1. Уравнения Максвелла и волновое уравнение. Рассмотрим однородную и изотропную, электрически нейтральную, непроводящую среду. Электромагнитное поле описывается уравнениями Максвелла:
Слайд 5
1.1. Уравнения Максвелла и волновое уравнение. Вычислим ротор от правой и левой части уравнения (1). В рассматриваемой среде ( ε = const., μ = const., = 0, = 0 ) эти уравнения можно переписать так: (1) (2) (3) (4)
Слайд 6
1.1. Уравнения Максвелла и волновое уравнение. После вычисления ротора от левой части уравнения (1) получаем: Согласно уравнению (4)
Слайд 7
1.1. Уравнения Максвелла и волновое уравнение. После вычисления ротора от правой и левой части уравнения (1) получаем: Согласно уравнению (3) Вычислим ротор от правой части уравнения (1).
Слайд 8
1.1. Уравнения Максвелла и волновое уравнение. Сравним полученное уравнение с общим видом дифференциального волнового уравнения: где v – фазовая скорость распространения волны. Полученное нами уравнение для напряжённости электрического поля совпадает волновым уравнением, если Решениями волнового уравнения являются плоские волны вида
Слайд 9
1.1. Уравнения Максвелла и волновое уравнение. Решениями волнового уравнения для вектора напряжённости электрического поля также являются плоские волны. В данном случае в пространстве распространяются колебания напряжённости электрического поля. Фазовая скорость распространения в пространстве таких колебаний: В вакууме, когда = 1 и = 1, (м/с).
Слайд 10
1.1. Уравнения Максвелла и волновое уравнение. Вычислим ротор от правой и левой части уравнения (3). Аналогично можно вывести волновое уравнение, рассматривая напряжённость магнитного поля. В рассматриваемой среде ( ε = const., μ = const., = 0, = 0 ) : (1) (2) (3) (4) Выполним преобразования, как и в предыдущем случае, воспользуемся уравнением (2) и получим:
Слайд 11
1.1. Уравнения Максвелла и волновое уравнение. Это уравнение можно переписать так: где - фазовая скорость волны. - решение волнового уравнения, уравнение плоской волны. Отметим, что решения одинаковы как для электрического поля, так и для магнитного. Колебания напряжённостей электрического и магнитного поле происходят одновременно и распространяются с одинаковой скоростью. Эти колебания совпадают по фазе. Колебания напряжённостей электрического и магнитного полей, распространяющиеся в пространстве, называются электромагнитными волнами.
Слайд 12
1.1. Уравнения Максвелла и волновое уравнение. Фазовая скорость электромагнитной волны В вакууме, когда ε = 1 и μ = 1, В некоторой среде, когда ε > 1 и μ > 1, В оптике величина n называется показателем преломления. Физический смысл показателя преломления - он показывает, во сколько раз скорость света (ЭМВ) в данной среде меньше, чем в вакууме.
Слайд 13
1.1. Уравнения Максвелла и волновое уравнение. Основные выводы: 1. Уравнения Максвелла допускают волновые решения. 2. Электромагнитная волна представляет собой колебания напряженностей электрического и магнитного полей, распространяющихся в пространстве. 3. Скорость распространения ЭМВ в вакууме 4. Скорость распространения ЭМВ в любой диэлектрической среде меньше, чем в вакууме: n – показатель преломления среды.
Слайд 15
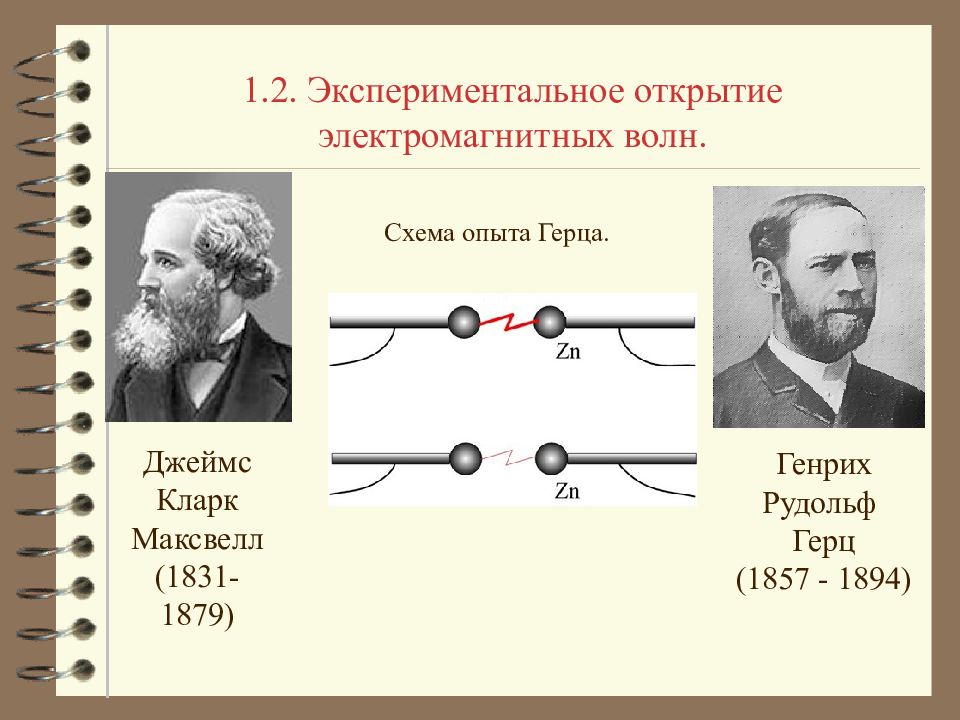
1.2. Экспериментальное открытие электромагнитных волн. Схема опыта Герца. Генрих Рудольф Герц (1857 - 1894) Джеймс Кларк Максвелл (1831-1879)
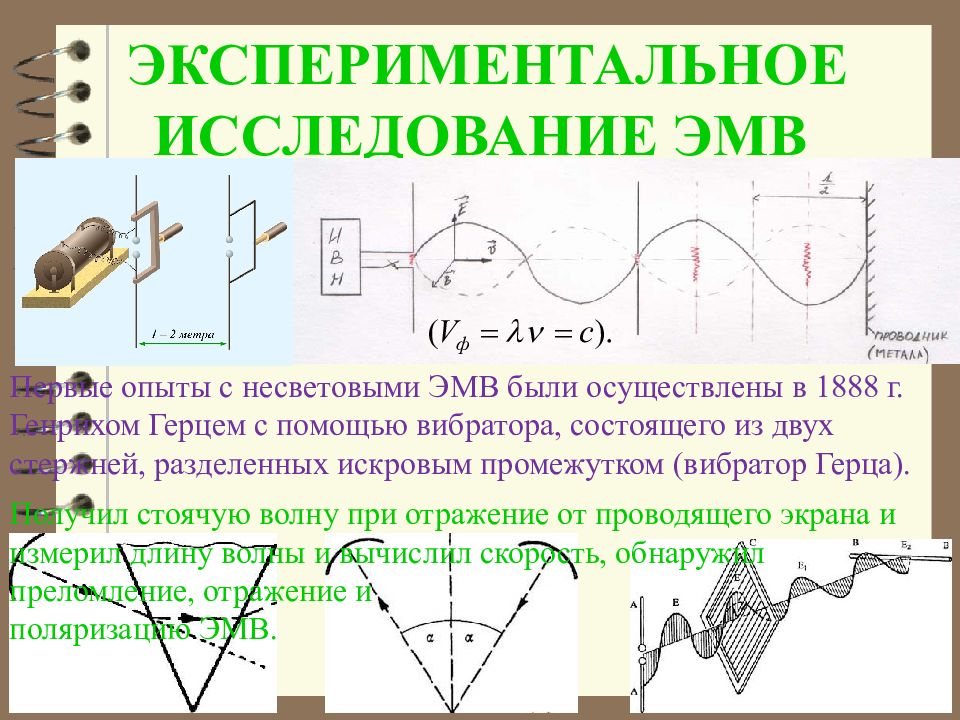
Слайд 16: ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ЭМВ
Первые опыты с несветовыми ЭМВ были осуществлены в 1888 г. Генрихом Герцем с помощью вибратора, состоящего из двух стержней, разделенных искровым промежутком (вибратор Герца). Получил стоячую волну при отражение от проводящего экрана и измерил длину волны и вычислил скорость, обнаружил преломление, отражение и поляризацию ЭМВ.
Слайд 18
1.3. Поперечность ЭМВ. 1. Скорость распространения ЭМВ в вакууме 2. Скорость распространения ЭМВ в любой диэлектрической среде меньше, чем в вакууме: n – показатель преломления среды. Некоторые свойства ЭМВ мы уже отметили: Ещё одним важнейшим свойством ЭМВ является её поперечность.
Слайд 19
1.3. Поперечность ЭМВ. Если плоская ЭМВ распространяется вдоль оси OX выбранной нами системы отсчёта, то её уравнение можно записать так: Здесь ω – циклическая (круговая) частота колебаний волны, k – волновое число. Известно, что волновые поверхности плоской волны - плоскости. Если волна распространяется вдоль оси OX, то её волновые поверхности есть плоскости, параллельные плоскости YZ (перпендикулярные OX).
Слайд 20
1.3. Поперечность ЭМВ. ЭМВ распространяется вдоль оси OX, изменение векторов E и H описывается уравнениями Каждая из волновых поверхностей характеризуется одним значением координаты X. Поэтому в пределах одной волновой поверхности в данный момент времени значения вектора напряжённости одинаковы. Это справедливо и для вектора E и для вектора H. Значения всех трёх компонент вектора E и всех трёх компонент вектора H зависят только от координаты X и не зависят от координат Y и Z.
Слайд 21
1.3. Поперечность ЭМВ. Рассмотрим уравнение, описывающее распространение ЭМВ: В левой части этого уравнения То же по компонентам:
Слайд 23
1.3. Поперечность ЭМВ. Величина E x, E y, E z зависит только от координаты x, поэтому
Слайд 24
1.3. Поперечность ЭМВ. В направлениях, перпендикулярных направлению распространения волны, производные по времен от H нулю не равны, следовательно, в этих направлениях может существовать переменное магнитное поле. В направлении, параллельном направлению распространения волны, может существовать только стационарное магнитное поле.
Слайд 25
1.3. Поперечность ЭМВ. Если рассмотреть уравнение, описывающее распространение ЭМВ и, как и в предыдущем случае, переписать его в виде проекций на оси координат, и учесть, что все компоненты вектора H зависят только от координаты x, получим В направлениях, перпендикулярных направлению распространения волны, может существовать переменное электрическое поле. В направлении, параллельном направлению распространения волны, может существовать только стационарное электрическое поле.
Слайд 26
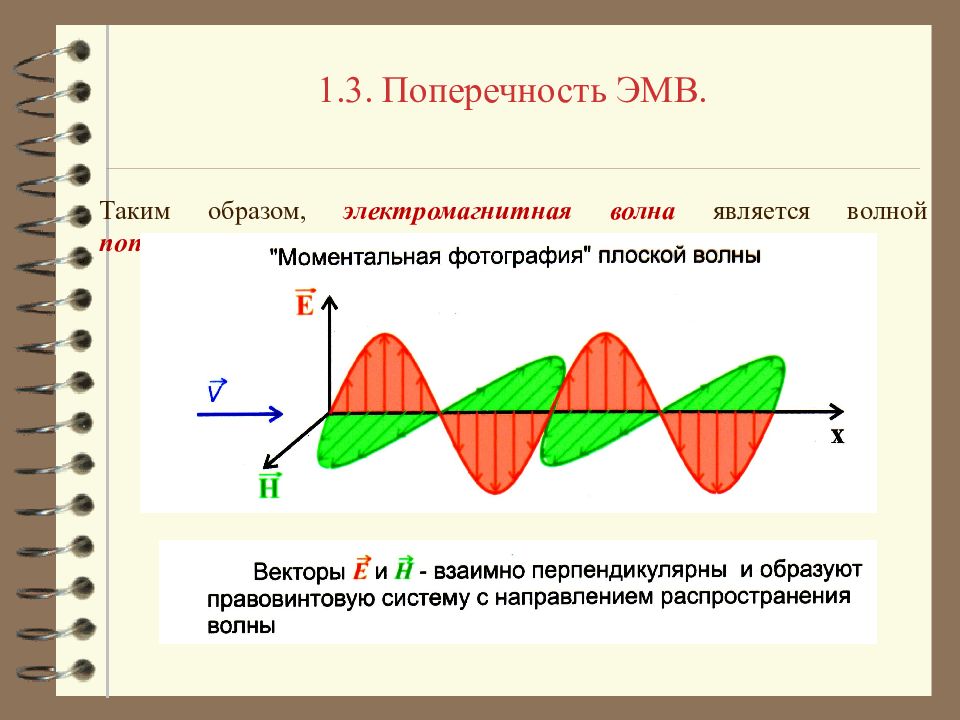
1.3. Поперечность ЭМВ. Таким образом, электромагнитная волна является волной поперечной.
Слайд 28
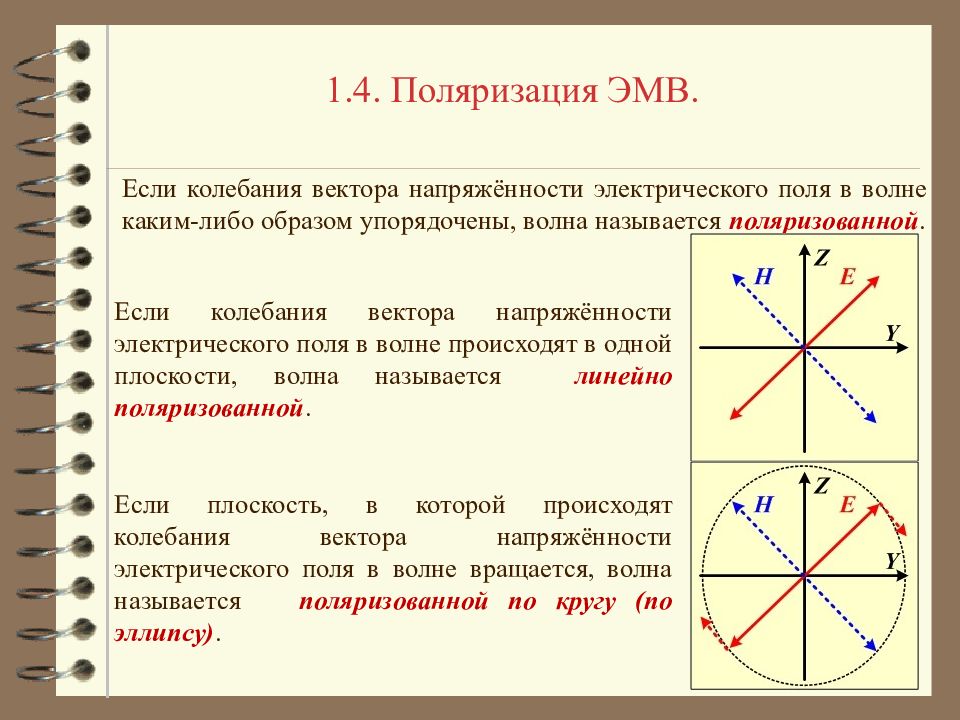
1.4. Поляризация ЭМВ. Если колебания вектора напряжённости электрического поля в волне каким-либо образом упорядочены, волна называется поляризованной. Если колебания вектора напряжённости электрического поля в волне происходят в одной плоскости, волна называется линейно поляризованной. Если плоскость, в которой происходят колебания вектора напряжённости электрического поля в волне вращается, волна называется поляризованной по кругу (по эллипсу).
Слайд 30
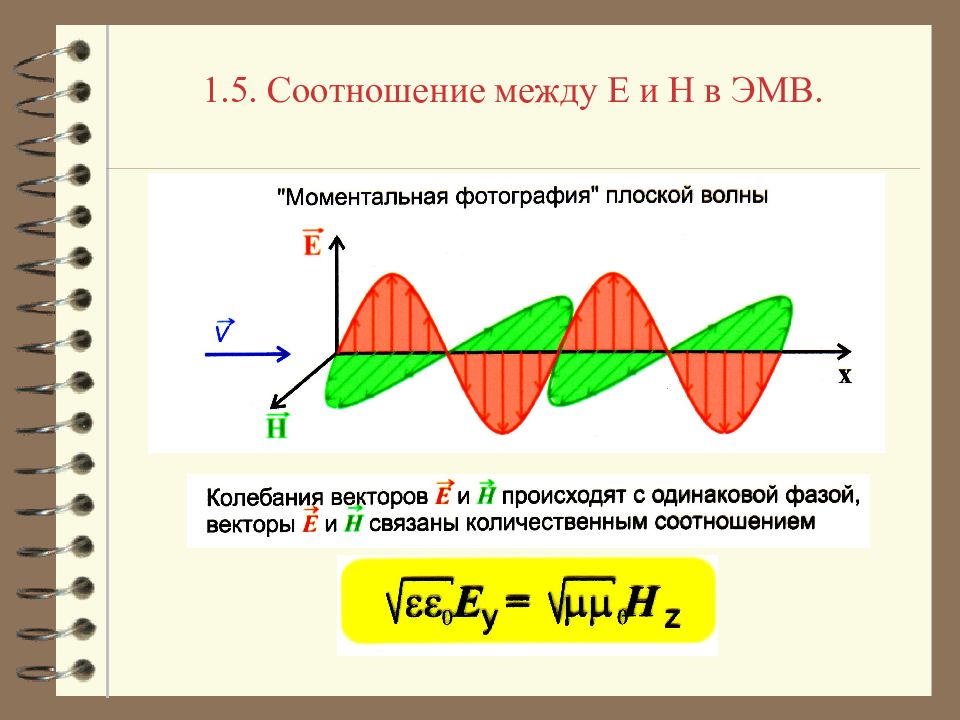
1.5. Соотношение между E и H в ЭМВ. Рассмотрим уравнение, описывающее распространение ЭМВ: В левой части этого уравнения
Слайд 31
1.5. Соотношение между E и H в ЭМВ. Учтём, что вектор E зависит только от координаты x Рассмотрим уравнение, описывающее распространение ЭМВ: В левой части этого уравнения
Слайд 32
1.5. Соотношение между E и H в ЭМВ. Учтём, что вектор H зависит только от координаты x Решениями волнового уравнения являются плоские волны (волна распространяется вдоль OX, векторы напряжённостей перпендикулярны)
Слайд 33
1.5. Соотношение между E и H в ЭМВ. Как мы установили ранее, Подставим в это уравнение выражения для напряжённостей полей. Это соотношение должно выполняться в любой момент времени и в точке с любой координатой x.
Слайд 34
1.5. Соотношение между E и H в ЭМВ. Волновое число k связано с циклической частотой ω соотношением