Лекция 15. Волновые процессы. Основные понятия. Волновые процессы. Основные понятия. Процесс распространения колебаний в сплошной среде называется волновым процессом или волной. Основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества. Волны делятся: - волны на поверхности жидкости; - упругие волны; - электромагнитные волны. Упругие волны – механические возмущения, распространяющиеся в упругой среде. Бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны. Могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т.е. в твердых, жидких и газообразных средах.
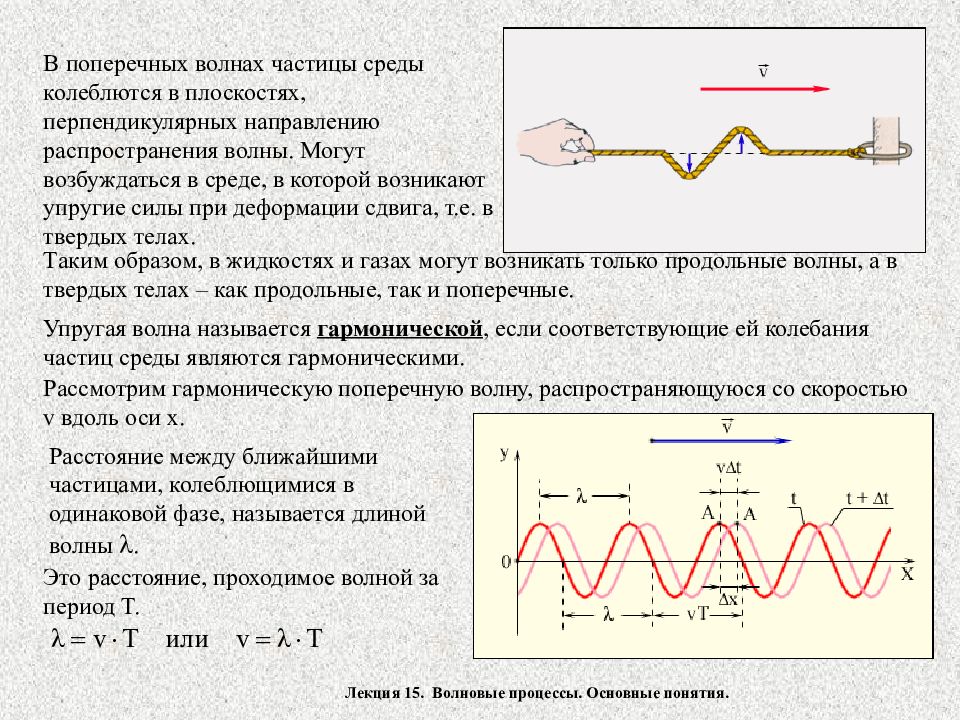
Лекция 15. Волновые процессы. Основные понятия. В поперечных волнах частицы среды колеблются в плоскостях, перпендикулярных направлению распространения волны. Могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т.е. в твердых телах. Таким образом, в жидкостях и газах могут возникать только продольные волны, а в твердых телах – как продольные, так и поперечные. Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Рассмотрим гармоническую поперечную волну, распространяющуюся со скоростью v вдоль оси х. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны . Это расстояние, проходимое волной за период Т.
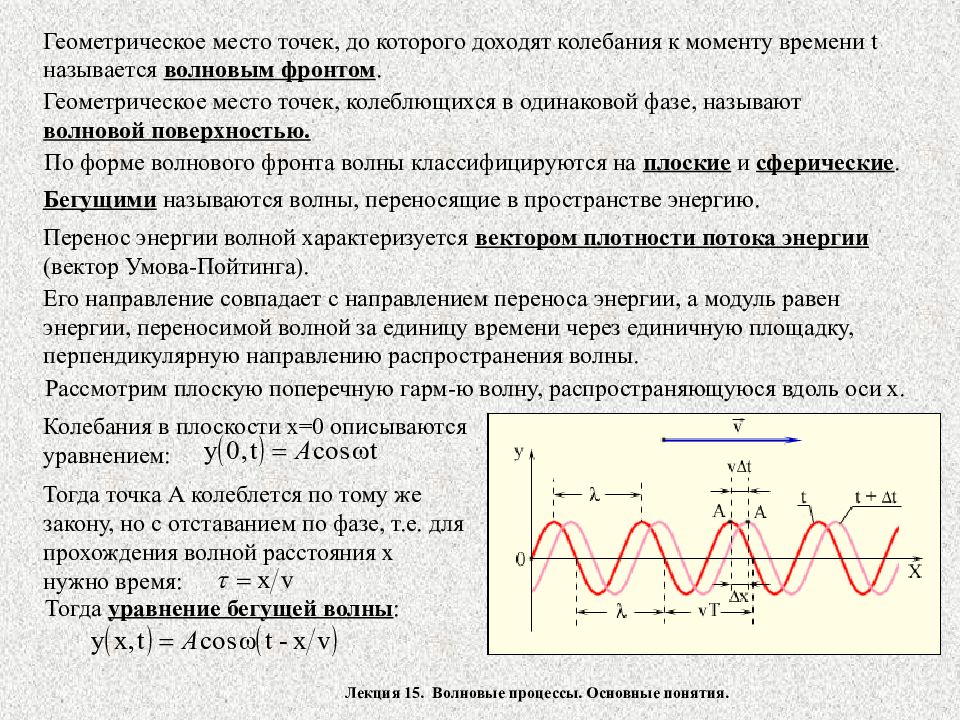
Лекция 15. Волновые процессы. Основные понятия. Геометрическое место точек, до которого доходят колебания к моменту времени t называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называют волновой поверхностью. По форме волнового фронта волны классифицируются на плоские и сферические. Бегущими называются волны, переносящие в пространстве энергию. Перенос энергии волной характеризуется вектором плотности потока энергии (вектор Умова-Пойтинга). Его направление совпадает с направлением переноса энергии, а модуль равен энергии, переносимой волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны. Рассмотрим плоскую поперечную гарм-ю волну, распространяющуюся вдоль оси х. Колебания в плоскости х=0 описываются уравнением: Тогда точка А колеблется по тому же закону, но с отставанием по фазе, т.е. для прохождения волной расстояния х нужно время: Тогда уравнение бегущей волны :
Лекция 15. Волновые процессы. Основные понятия. Если волна распространяется в противоположном направлении, то ее уравнение: В общем случае уравнение плоской бегущей волны, распространяющейся вдоль оси х: А – амплитуда волны; - циклическая частота; 0 – начальная фаза волны. Волна характеризуется волновым числом : Тогда уравнение волны: Уравнение волны в комплексной форме : Пусть при волновом процессе фаза волны константа: Продифференцируем фазу по времени: Скорость распространения волны v есть скорость перемещения фазы волны или фазовая скорость. Если v зависит от частоты волны, то имеется дисперсия волн. Уравнение сферической волны : где r – расстояние от центра волны до рассматриваемой точки среды. В сферической волне даже без поглощения энергия убывает с расстоянием пропорционально 1/ r.
Лекция 15. Волновые процессы. Основные понятия. В общем случае в однородной изотропной среде волновое уравнение: где Δ – оператор Лапласа Для плоской волны: Принцип суперпозиции волн : при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие отсутствуют. Результирующее смещение частиц среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из волновых процессов. Следствие: любая волна может быть представлена в виде суммы гармонических волн, т.е. в виде волнового пакета или группы волн. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства. Рассмотрим простейший волновой пакет из двух гармонических волн с одинаковой амплитудой, близкими частотами и волновыми числами.
Лекция 15. Волновые процессы. Основные понятия. Тогда можно записать суперпозицию исходных волн: Эта волна отличается от гармонической тем, что ее амплитуда есть медленно меняющаяся функция от координаты и времени. За скорость распространения волнового пакета принимают скорость перемещения максимума амплитуды волны. Из условия, что фаза амплитуды пакета равна константе найдем групповую скорость: Связь между фазовой и групповой скоростью: Групповая скорость может быть как меньше, так и больше фазовой в зависимости от знака В недиспергирующей среде Групповая скорость используется в эхо – и радиолокации, радиосвязи. Групповая скорость меньше скорости света в данной среде. Для фазовой скорости таких ограничений не существует.
Лекция 16. Суперпозиция волн Интерференция волн. Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов называют когерентностью. Волны называются когерентными, если разность фаз между ними остается постоянной во времени. Интерференция: при наложении в пространстве двух или нескольких когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами исходных волн. Рассмотрим сложение двух когерентных сферических волн от точечных источников S1 и S2, колеблющихся с одинаковой амплитудой и частотой. где r 1 и r 2 – расстояния от источников до точки В.
Лекция 16. Суперпозиция волн Амплитуда результирующей волны: Поскольку 1 - 2 = const то амплитуда зависит от r 1 - r 2 = Δ, называемой разностью хода. В точках, где: наблюдается интерференционный максимум В точках, где: с амплитудой наблюдается интерференционный минимум с амплитудой число m называют порядком интерференционного максимума или минимума. Частным случаем интерференции является образование стоячих волн.
Лекция 16. Суперпозиция волн Стоячие волны Стоячая волна образуется при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами, амплитудами, а для поперечных волн и поляризациями. Пусть две плоские волны распространяются навстречу друг другу вдоль оси x в среде без затухания, амплитуда и частота волн одинакова. Выберем начало отсчета чтобы 1 = 2 = 0. Тогда уравнение волн: Сложим эти колебания: В каждой точке волны происходят колебания с частотой и амплитудой, зависящей от ее координаты х: В точках среды, где:
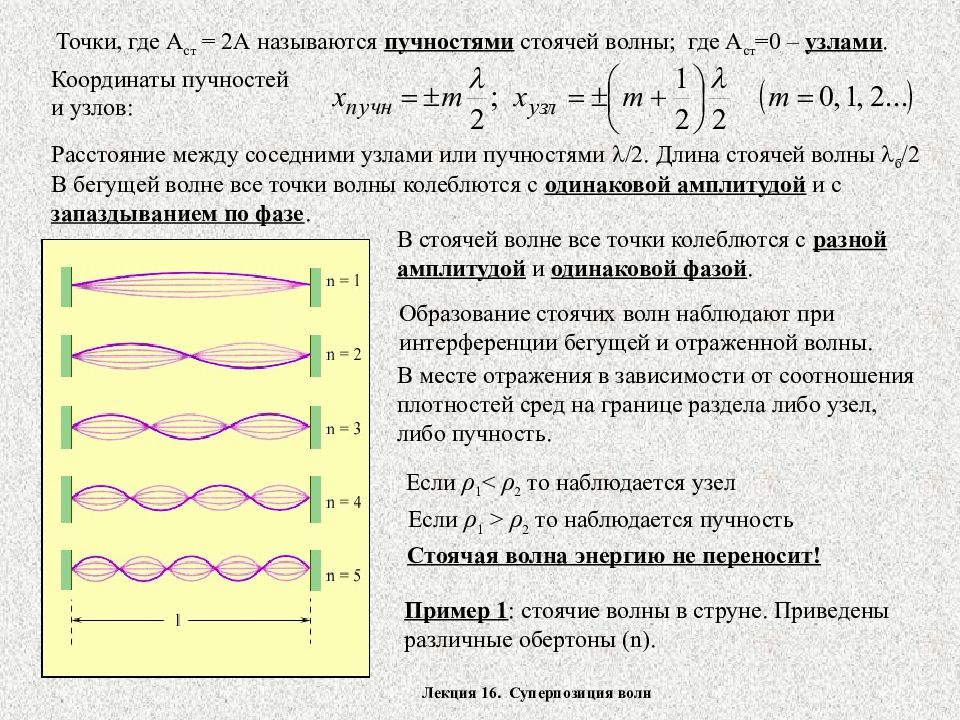
Лекция 16. Суперпозиция волн Точки, где A ст = 2А называются пучностями стоячей волны; где А ст =0 – узлами. Координаты пучностей и узлов: Расстояние между соседними узлами или пучностями /2. Длина стоячей волны б /2 В бегущей волне все точки волны колеблются с одинаковой амплитудой и с запаздыванием по фазе. В стоячей волне все точки колеблются с разной амплитудой и одинаковой фазой. Образование стоячих волн наблюдают при интерференции бегущей и отраженной волны. В месте отражения в зависимости от соотношения плотностей сред на границе раздела либо узел, либо пучность. Если ρ 1 < ρ 2 то наблюдается узел Если ρ 1 > ρ 2 то наблюдается пучность Стоячая волна энергию не переносит! Пример 1 : стоячие волны в струне. Приведены различные обертоны ( n).
Лекция 16. Суперпозиция волн Пример 2 : стоячие волны в органной трубе. Приведены различные обертоны ( n). Пример 3 : стоячие волны на плоскости (фигуры Хладни). В пластине, закрепленной в одной точке и посыпанной песком смычком возбуждают стоячие волны. Песок скапливается в узловых точках.
Лекция 17. Элементы акустики Звуковые волны Звуковыми или акустическими волнами называются распространяющиеся в среде упругие волны, обладающие частотами от 16 Гц до 20000 Гц. Эти волны, воздействуя на слуховой аппарат человека, вызывают ощущение звука. При частоте волны ниже 16 Гц волны называют инфразвуком, при частоте выше 20000 Гц – ультразвуком. Звуковые волны в газах и жидкостях могут быть только продольными. В твердых телах – как продольными, так и поперечными.
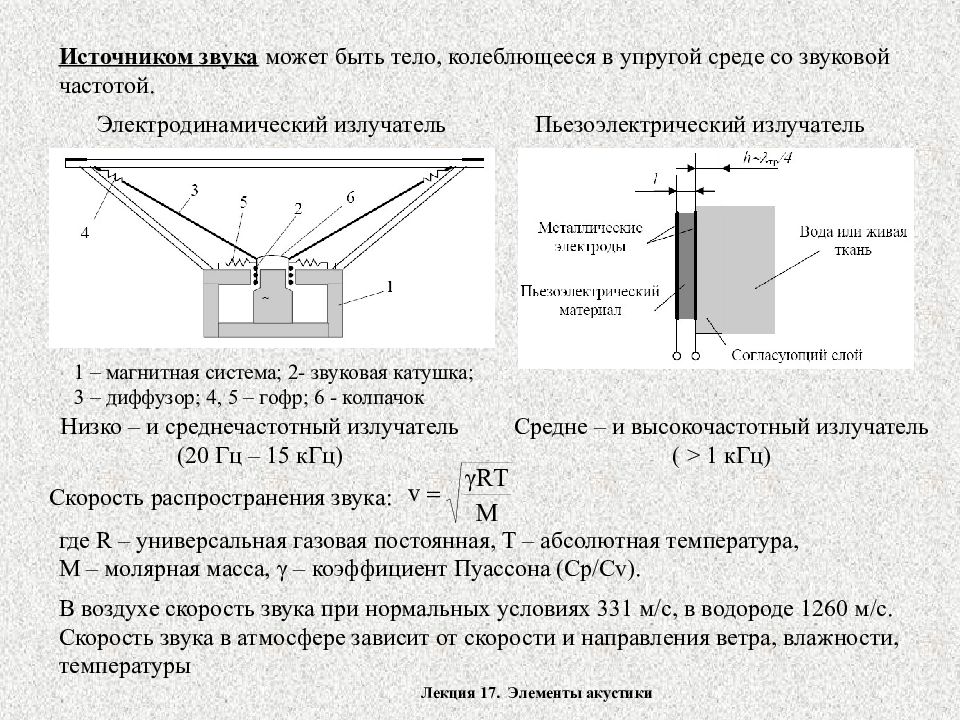
Источником звука может быть тело, колеблющееся в упругой среде со звуковой частотой. Электродинамический излучатель Пьезоэлектрический излучатель 1 – магнитная система; 2- звуковая катушка; 3 – диффузор; 4, 5 – гофр; 6 - колпачок Низко – и среднечастотный излучатель (20 Гц – 15 кГц) Средне – и высокочастотный излучатель ( > 1 кГц ) Скорость распространения звука: где R – универсальная газовая постоянная, T – абсолютная температура, M – молярная масса, γ – коэффициент Пуассона ( Cp/Cv). Лекция 17. Элементы акустики В воздухе скорость звука при нормальных условиях 331 м/с, в водороде 1260 м/с. Скорость звука в атмосфере зависит от скорости и направления ветра, влажности, температуры
Объективные и субъективные амплитудные характеристики звука Лекция 17. Элементы акустики Интенсивностью (силой звука) называют среднюю по времени энергию, переносимую звуковой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны. Чувствительность человеческого уха зависит от частоты звука. Для каждой частоты есть наименьшая интенсивность, называемая порогом слышимости и наибольшая, называемая порогом болевого ощущения. Интенсивность звука – объективная характеристика. Громкость звука – субъективная характеристика. Согласно физиологическому закону Вебера-Фехнера, с ростом интенсивности громкость возрастает по логарифмическому закону. Рассмотрим переход от объективных к субъективным характеристикам. Уровень интенсивности звука: где I 0 - интенсивность звука на пороге слышимости.
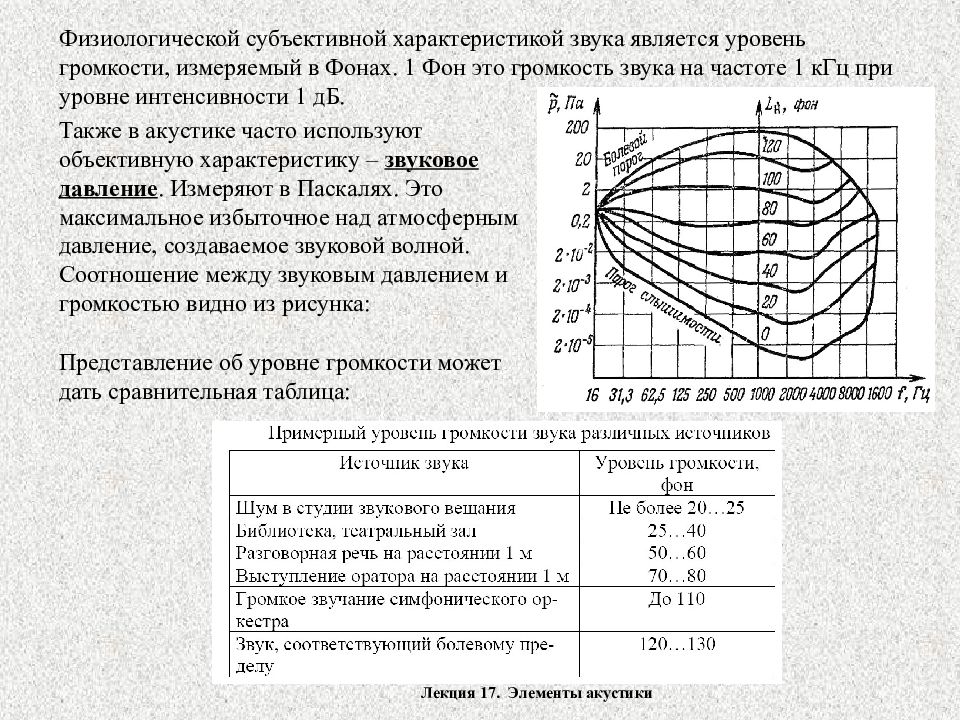
Лекция 17. Элементы акустики Физиологической субъективной характеристикой звука является уровень громкости, измеряемый в Фонах. 1 Фон это громкость звука на частоте 1 кГц при уровне интенсивности 1 дБ. Также в акустике часто используют объективную характеристику – звуковое давление. Измеряют в Паскалях. Это максимальное избыточное над атмосферным давление, создаваемое звуковой волной. Соотношение между звуковым давлением и громкостью видно из рисунка: Представление об уровне громкости может дать сравнительная таблица:
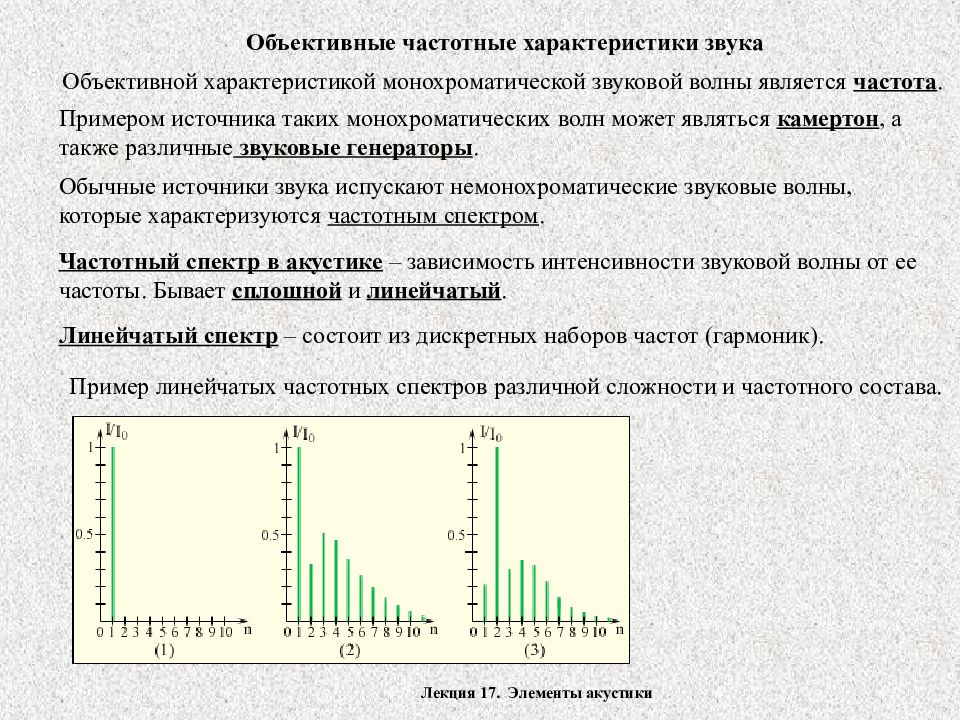
Лекция 17. Элементы акустики Объективные частотные характеристики звука Объективной характеристикой монохроматической звуковой волны является частота. Примером источника таких монохроматических волн может являться камертон, а также различные звуковые генераторы. Обычные источники звука испускают немонохроматические звуковые волны, которые характеризуются частотным спектром. Частотный спектр в акустике – зависимость интенсивности звуковой волны от ее частоты. Бывает сплошной и линейчатый. Линейчатый спектр – состоит из дискретных наборов частот (гармоник). Пример линейчатых частотных спектров различной сложности и частотного состава.
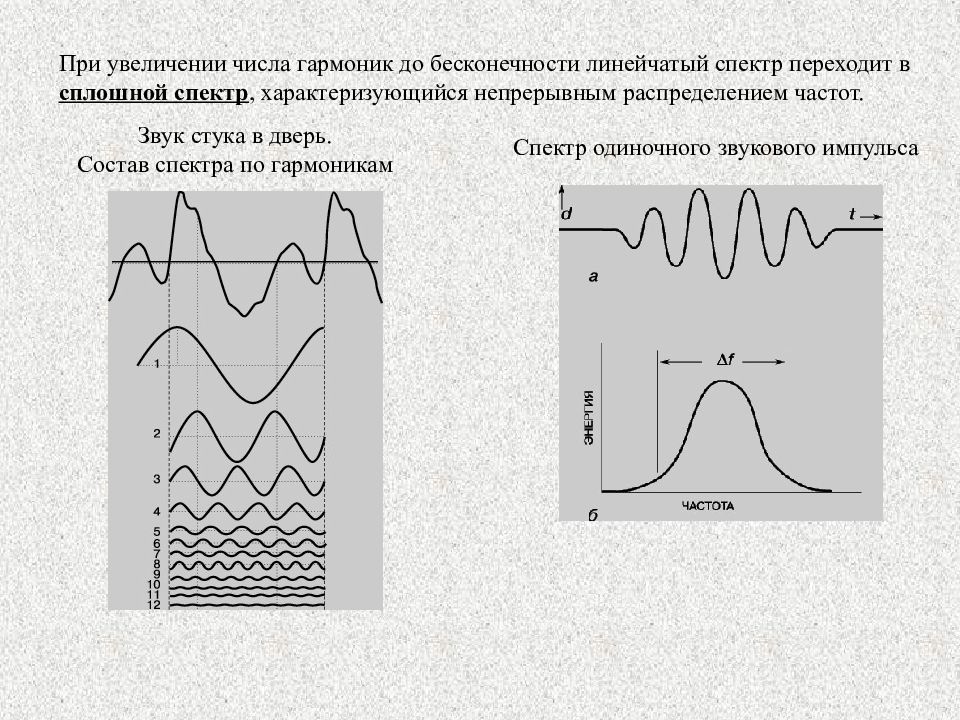
При увеличении числа гармоник до бесконечности линейчатый спектр переходит в сплошной спектр, характеризующийся непрерывным распределением частот. Спектр одиночного звукового импульса Звук стука в дверь. Состав спектра по гармоникам
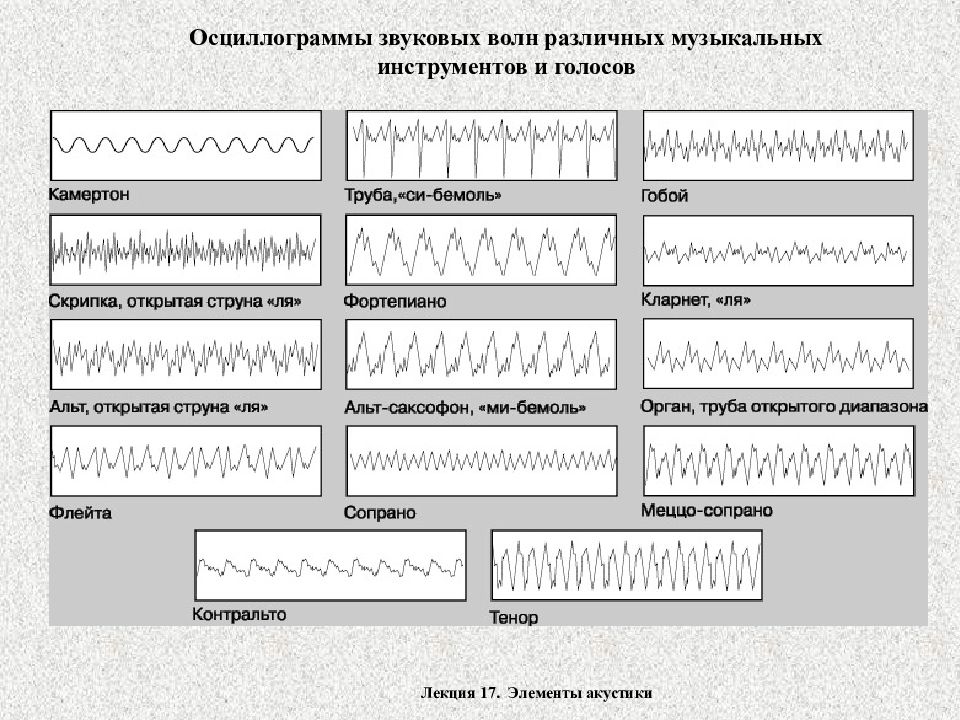
Лекция 17. Элементы акустики Осциллограммы звуковых волн различных музыкальных инструментов и голосов
Лекция 17. Элементы акустики Частотные спектры звуковых волн различных музыкальных инструментов
Лекция 17. Элементы акустики Субъективные частотные характеристики звука Субъективной частотной характеристикой монохроматической звуковой волны является высота звука. Высота звука – качество звука, определяемое человеком на слух и зависящее от частоты звука. Субъективной частотной характеристикой немонохроматической звуковой волны является тембр звука. Характер акустического спектра и распределение энергии между определенными частотами определяет тембр звука. Помещение в акустике характеризуется ревебрацией – постепенным затуханием звука в закрытом помещении после выключения источника. Время ревебрации – время, в течение которого интенсивность звука в помещении ослабляется в миллион раз (уровень интенсивности уменьшается на 60 дБ). Помещение с хорошей акустикой, если время ревебрации 0.5 – 1.5 с.
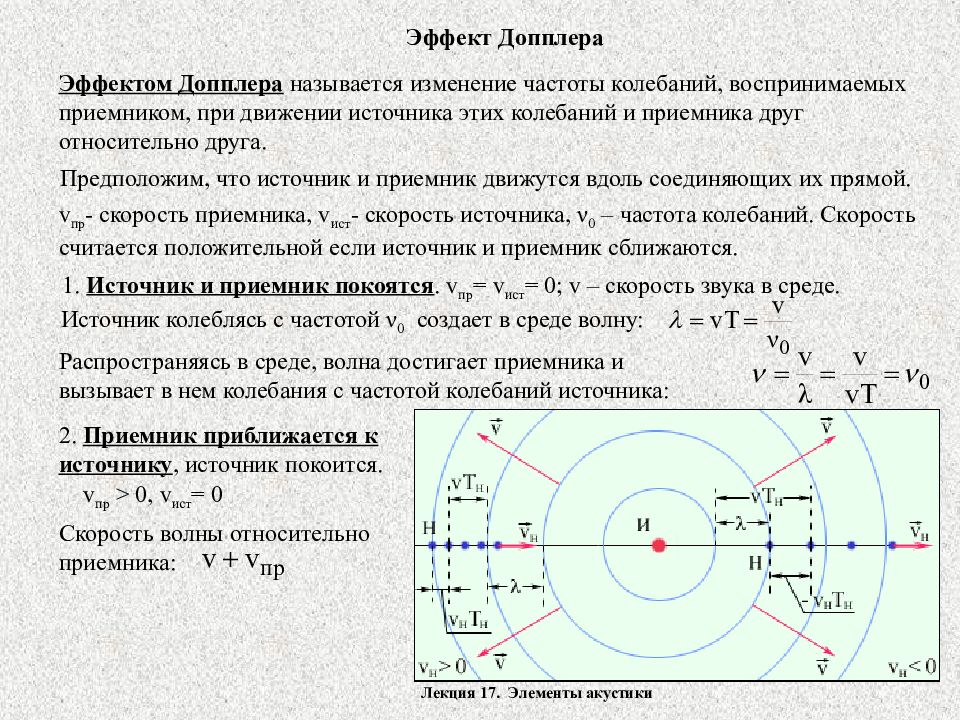
Лекция 17. Элементы акустики Эффект Допплера Эффектом Допплера называется изменение частоты колебаний, воспринимаемых приемником, при движении источника этих колебаний и приемника друг относительно друга. Предположим, что источник и приемник движутся вдоль соединяющих их прямой. v пр - скорость приемника, v ист - скорость источника, ν 0 – частота колебаний. Скорость считается положительной если источник и приемник сближаются. 1. Источник и приемник покоятся. v пр = v ист = 0; v – скорость звука в среде. Распространяясь в среде, волна достигает приемника и вызывает в нем колебания с частотой колебаний источника: Источник колеблясь с частотой ν 0 создает в среде волну: 2. Приемник приближается к источнику, источник покоится. v пр > 0, v ист = 0 Скорость волны относительно приемника:
Лекция 17. Элементы акустики Т.к. длина волны при этом не меняется, то частота приемника: При сближении приемника и источника (источник покоится) частота регистрируемых колебаний увеличилась. 3. Источник приближается к приемнику, приемник покоится. v ист > 0, v пр = 0 Скорость распространения волны v, за период она проходит расстояние vT. За это же время источник в направлении распространения волны v ист T. При этом длина волны в направлении движения сократится и станет равной: Тогда частота на приемнике: 4. Источник и приемник движутся навстречу друг другу.
