Первый слайд презентации: Вписанные многоугольники
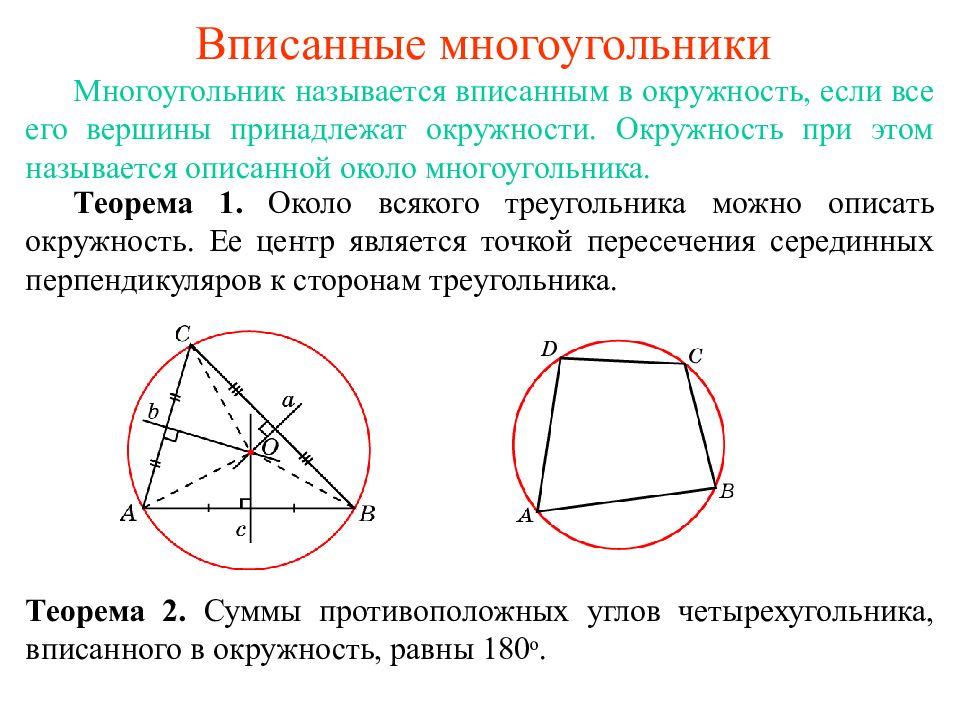
Многоугольник называется вписанным в окружность, если все его вершины принадлежат окружности. Окружность при этом называется описанной около многоугольника. Теорема 1. Около всякого треугольника можно описать окружность. Ее центр является точкой пересечения серединных перпендикуляров к сторонам треугольника. Теорема 2. Суммы противоположных углов четырехугольника, вписанного в окружность, равны 180 о.
Слайд 2: Описанные многоугольники
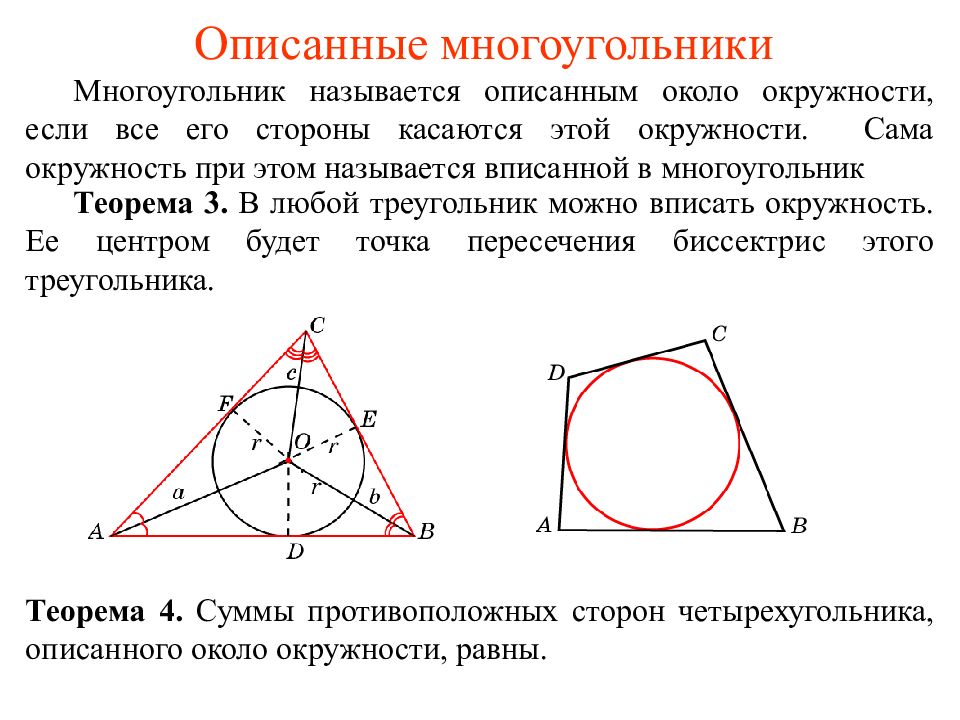
Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности. Сама окружность при этом называется вписанной в многоугольник Теорема 3. В любой треугольник можно вписать окружность. Ее центром будет точка пересечения биссектрис этого треугольника. Теорема 4. Суммы противоположных сторон четырехугольника, описанного около окружности, равны.
Слайд 3: Вписанные и описанные треугольники
Теорема 5. Отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности. Теорема 7. Радиус r окружности, вписанной в треугольник, выражается формулой, где a, b, c – стороны треугольника S – его площадь. Теорема 6. Радиус R окружности, описанной около правильного треугольника, выражается формулой, где a, b, c – стороны треугольника S – его площадь.
Слайд 4: Упражнение 1
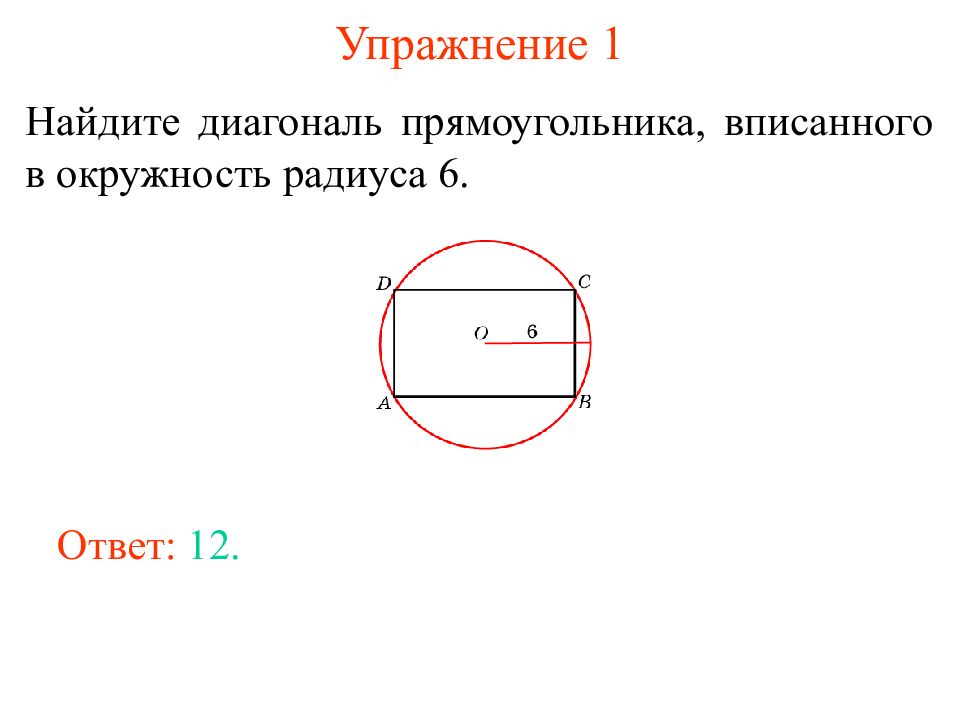
Найдите диагональ прямоугольника, вписанного в окружность радиуса 6. Ответ: 12.
Слайд 5: Упражнение 2
Найдите радиус окружности, описанной около квадрата со стороной, равной. Ответ: 1.
Слайд 6: Упражнение 3
Меньшая сторона прямоугольника равна 5 см. Угол между диагоналями равен 60 о. Найдите радиус описанной окружности. Ответ: 5.
Слайд 7: Упражнение 4
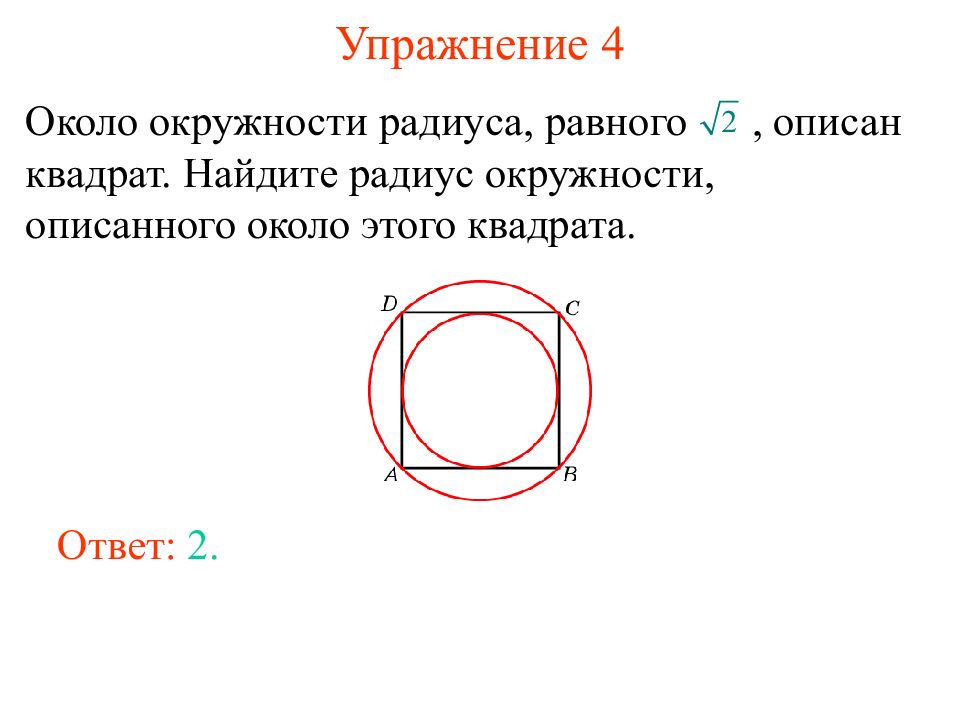
Около окружности радиуса, равного, описан квадрат. Найдите радиус окружности, описанного около этого квадрата. Ответ: 2.
Слайд 8: Упражнение 5
Боковые стороны трапеции, описанной около окружности, равны 2 и 4. Найдите среднюю линию трапеции. Ответ: 3.
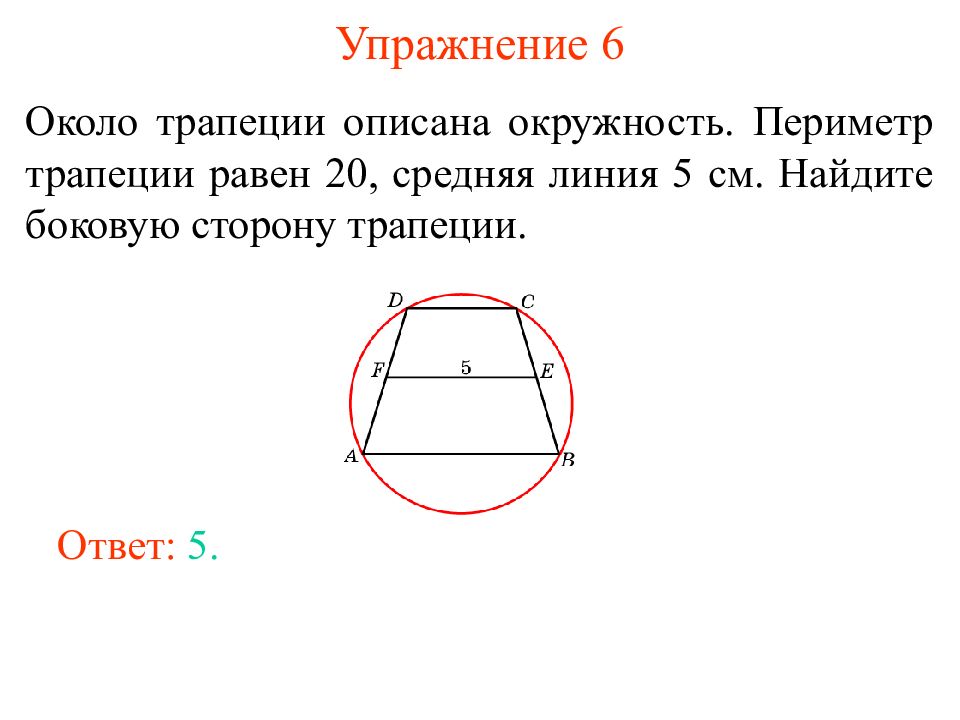
Слайд 9: Упражнение 6
Около трапеции описана окружность. Периметр трапеции равен 20, средняя линия 5 см. Найдите боковую сторону трапеции. Ответ: 5.
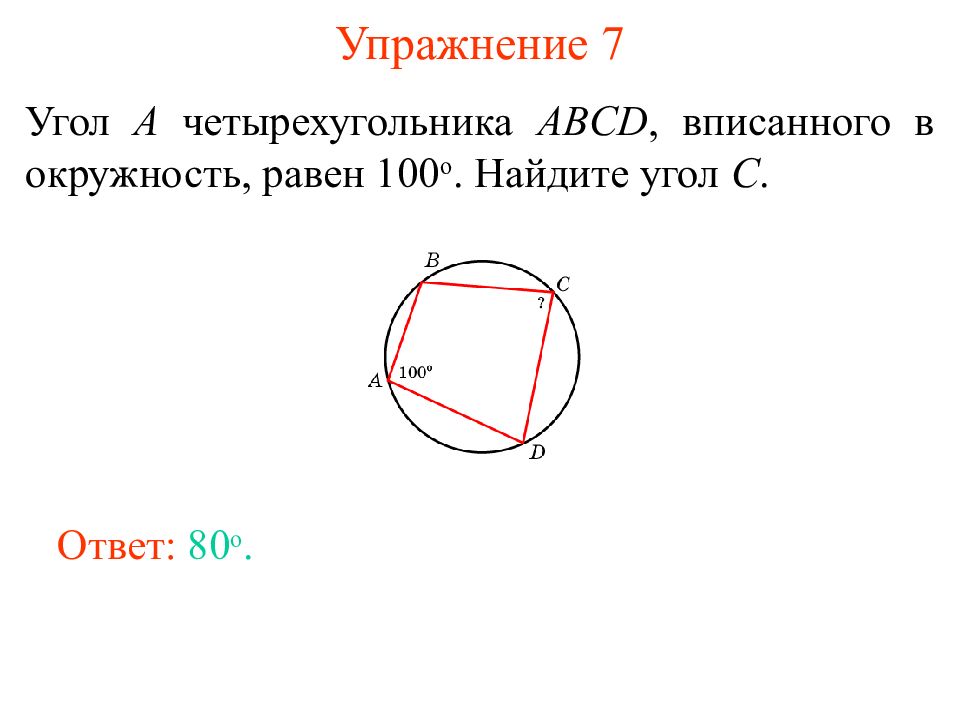
Слайд 10: Упражнение 7
Угол A четырехугольника ABCD, вписанного в окружность, равен 100 о. Найдите угол C. Ответ: 80 о.
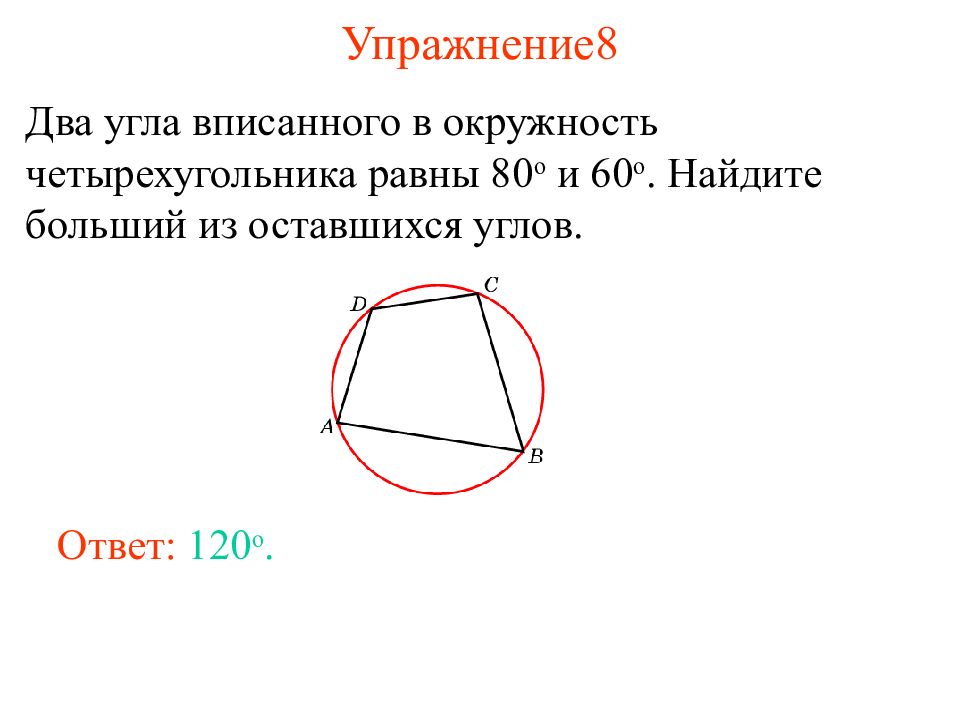
Слайд 11: Упражнение 8
Два угла вписанного в окружность четырехугольника равны 80 о и 60 о. Найдите больший из оставшихся углов. Ответ: 120 о.
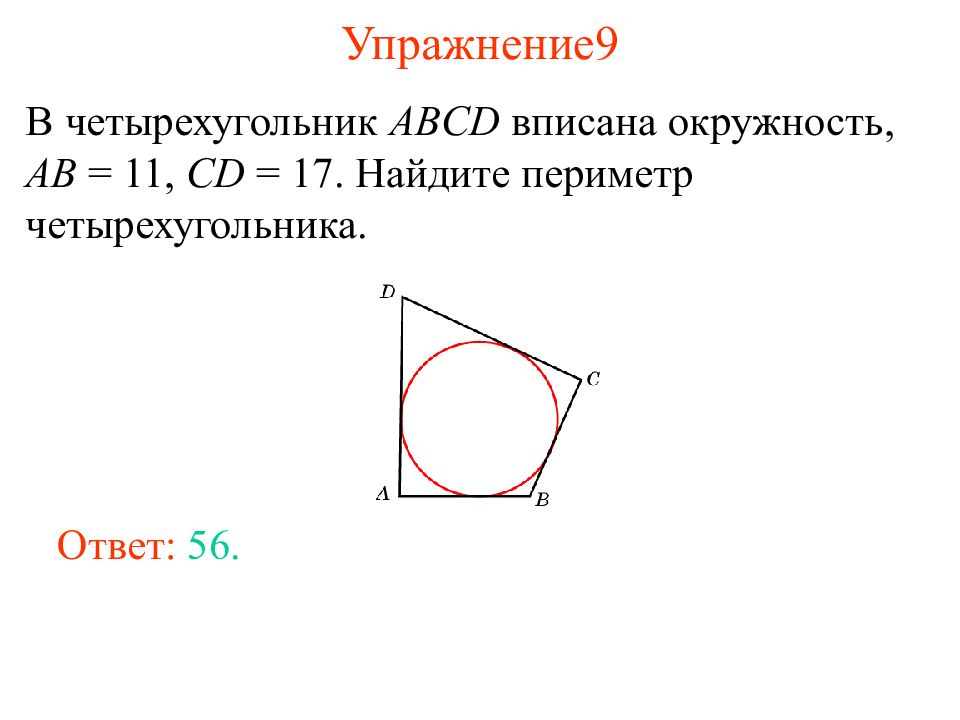
Слайд 12: Упражнение 9
В четырехугольник ABCD вписана окружность, AB = 11, CD = 17. Найдите периметр четырехугольника. Ответ: 56.
Слайд 13: Упражнение 1 0
Периметр четырехугольника, описанного около окружности, равен 20, две его стороны равны 4 и 5. Найдите большую из оставшихся сторон. Ответ: 6.
Слайд 14: Упражнение 1 1
В четырехугольник ABCD вписана окружность, AB = 11, BC = 10 и CD = 15. Найдите четвертую сторону четырехугольника. Ответ: 16.
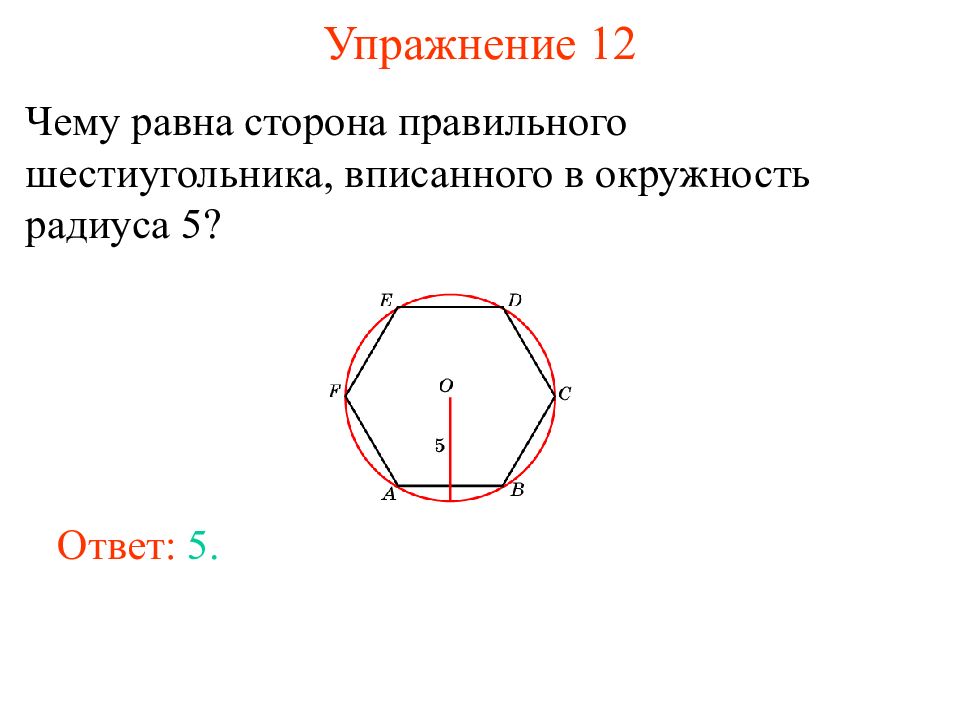
Слайд 15: Упражнение 1 2
Чему равна сторона правильного шестиугольника, вписанного в окружность радиуса 5? Ответ: 5.
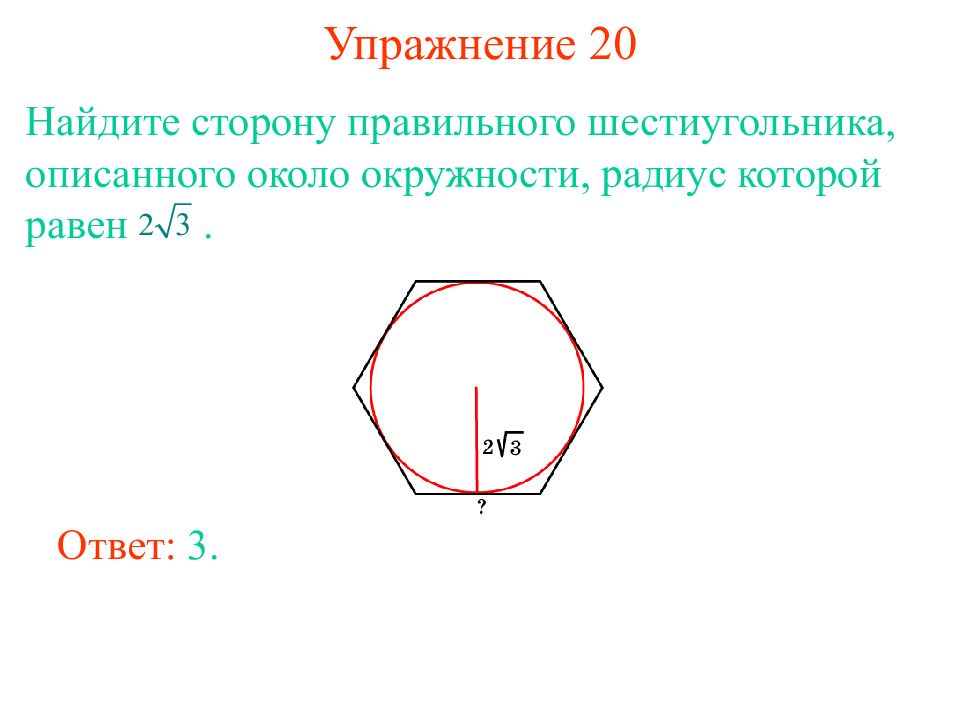
Слайд 16: Упражнение 20
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен. Ответ: 3.
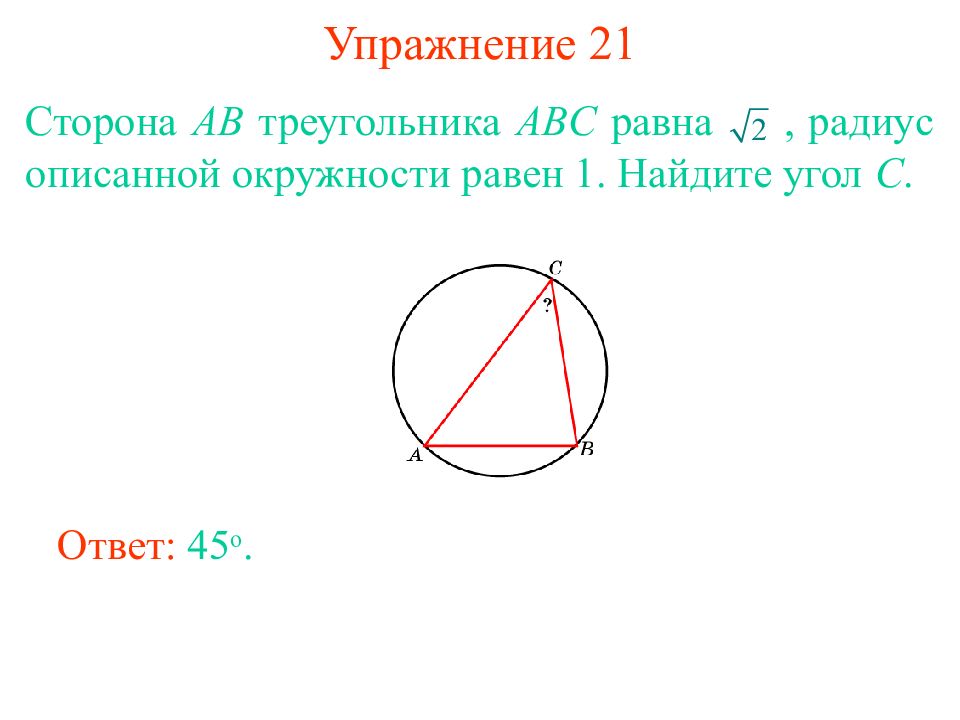
Слайд 17: Упражнение 21
Сторона AB треугольника ABC равна, радиус описанной окружности равен 1. Найдите угол C. Ответ: 45 о.
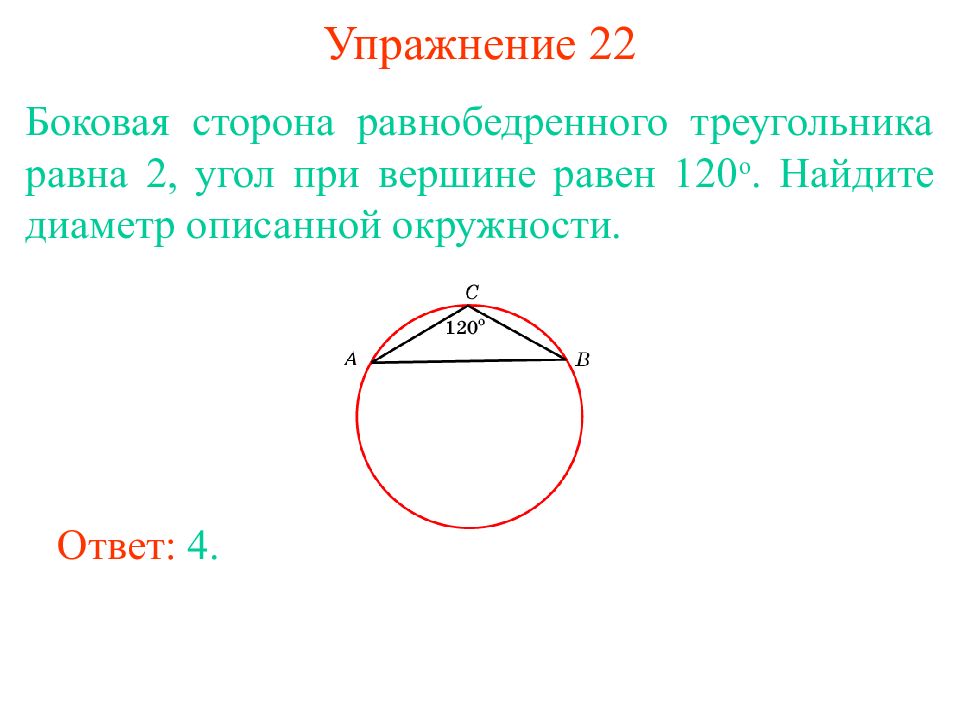
Слайд 18: Упражнение 22
Боковая сторона равнобедренного треугольника равна 2, угол при вершине равен 120 о. Найдите диаметр описанной окружности. Ответ: 4.
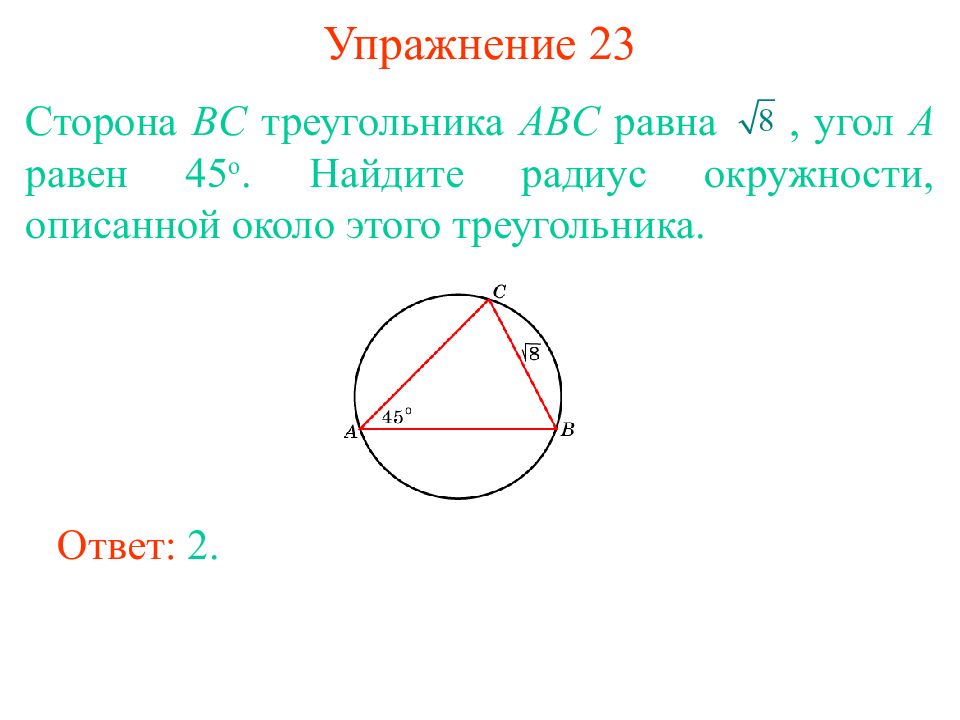
Слайд 19: Упражнение 23
Сторона BC треугольника ABC равна, угол A равен 45 о. Найдите радиус окружности, описанной около этого треугольника. Ответ: 2.
Слайд 20: Упражнение 24
Сторона AB треугольника ABC равна 10, радиус описанной окружности равен 10. Найдите угол C. Ответ: 150 о.
Слайд 21: Упражнение 25
Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности. Ответ: 25.
Слайд 22: Упражнение 26
В треугольнике ABC AC = 8, BC = 6, угол C равен 90 о. Найдите радиус вписанной окружности. Ответ: 2.
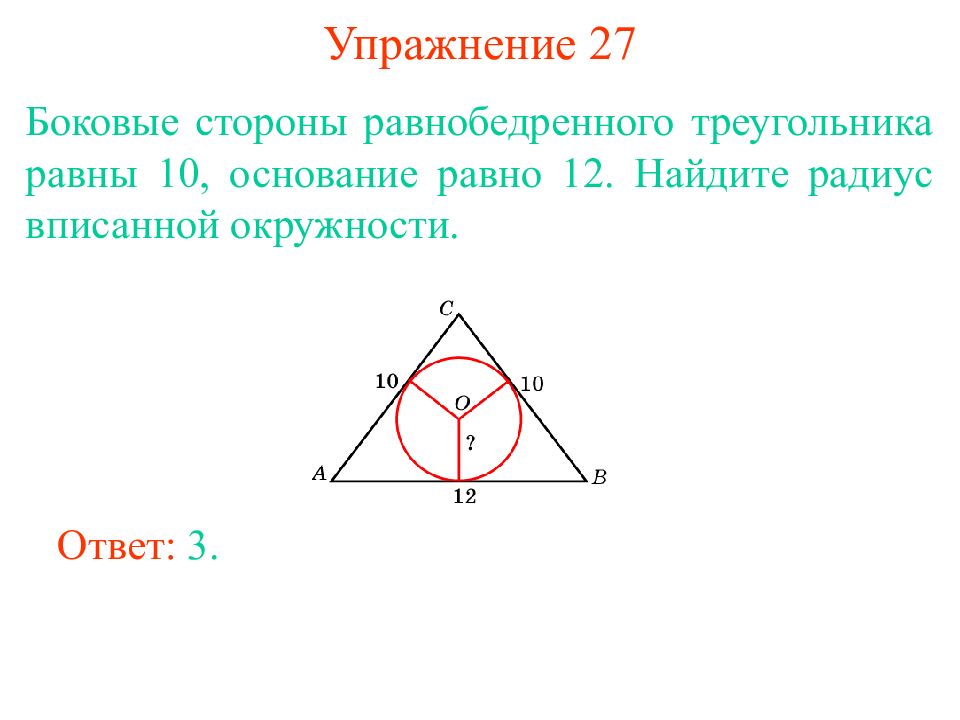
Слайд 23: Упражнение 27
Боковые стороны равнобедренного треугольника равны 10, основание равно 12. Найдите радиус вписанной окружности. Ответ: 3.
Слайд 24: Упражнение 28
Боковые стороны равнобедренного треугольника равны, основание равно 6. Найдите радиус описанной окружности. Ответ: 5.
Слайд 25: Упражнение 29
Сторона AB треугольника ABC равна 10. Найдите радиус описанной около этого треугольника окружности, если противолежащий этой стороне угол C равен 150 о. Ответ: 10.
Слайд 26: Упражнение 30
Около окружности описана трапеция, периметр которой равен 36. Найдите ее среднюю линию. Ответ: 9.
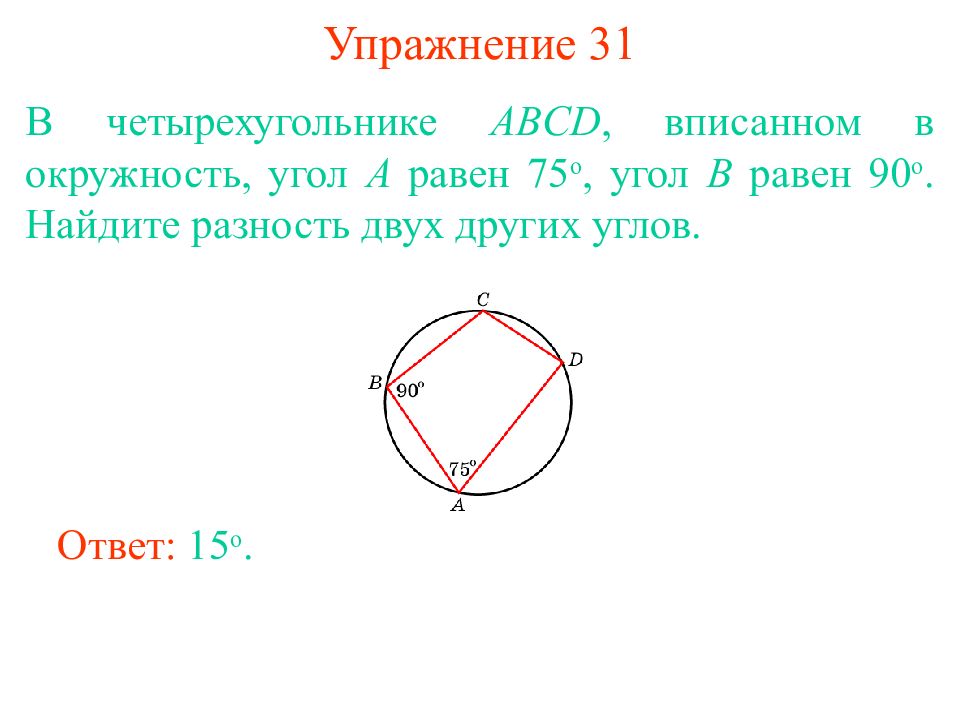
Слайд 27: Упражнение 31
В четырехугольнике ABCD, вписанном в окружность, угол A равен 75 о, угол B равен 90 о. Найдите разность двух других углов. Ответ: 15 о.
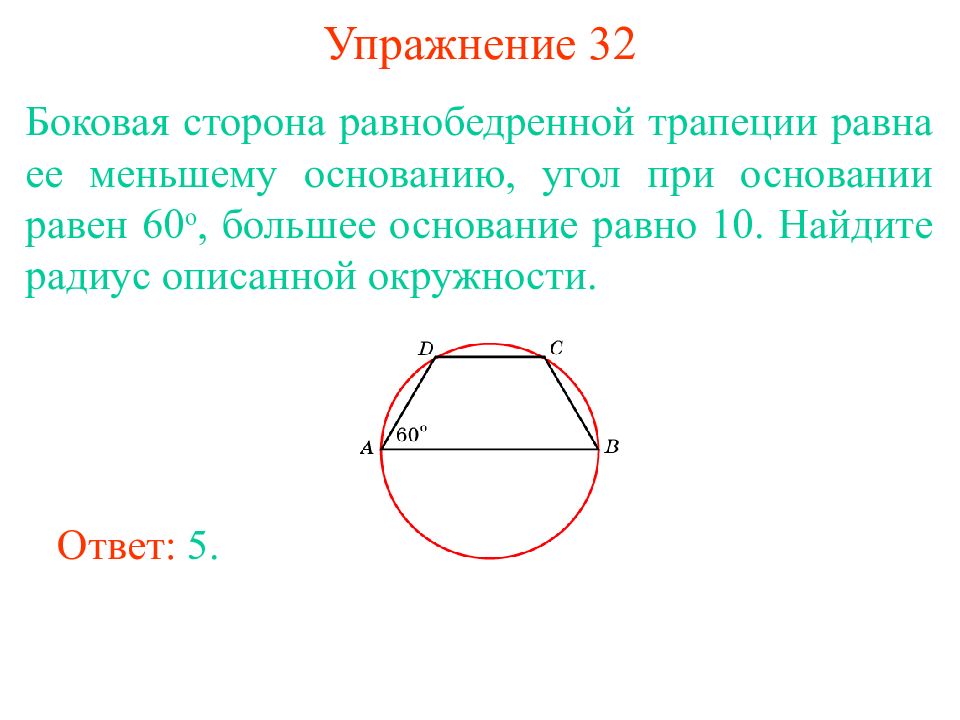
Слайд 28: Упражнение 32
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 о, большее основание равно 10. Найдите радиус описанной окружности. Ответ: 5.
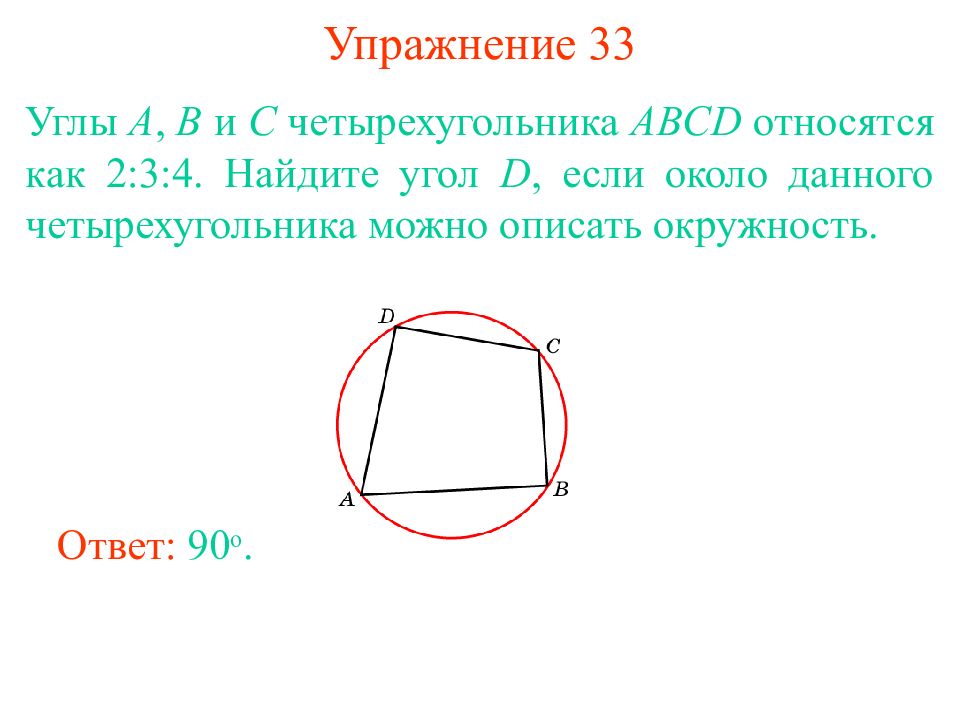
Слайд 29: Упражнение 33
Углы A, B и C четырехугольника ABCD относятся как 2:3:4. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ: 90 о.
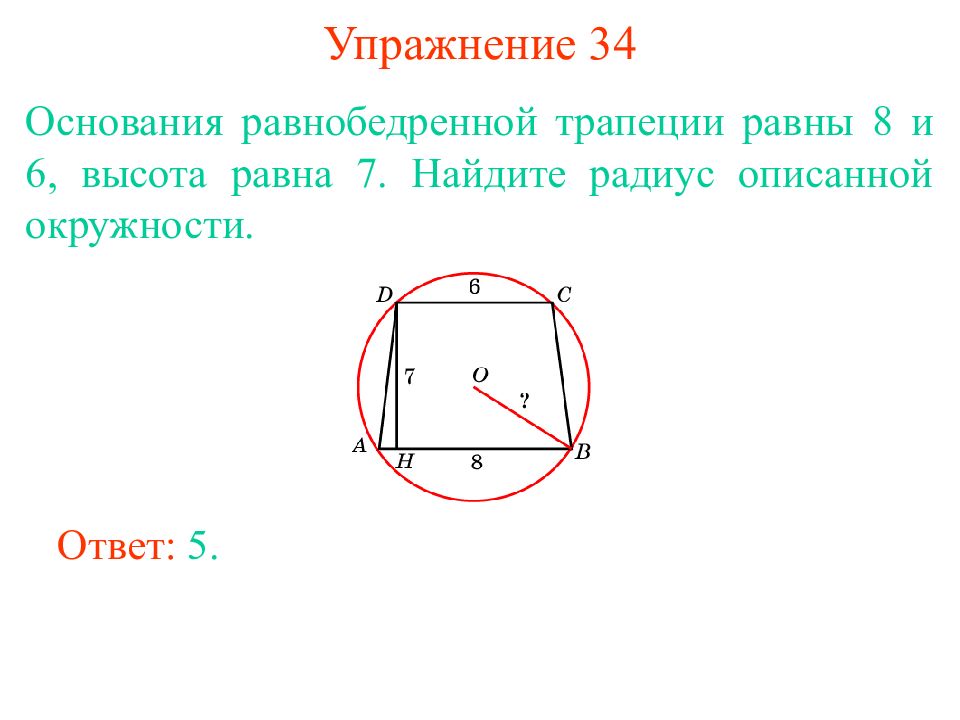
Слайд 30: Упражнение 34
Основания равнобедренной трапеции равны 8 и 6, высота равна 7. Найдите радиус описанной окружности. Ответ: 5.
Слайд 31: Упражнение 35
Периметр прямоугольной трапеции, описанной около окружности, равен 20, ее большая боковая сторона равна 6. Найдите радиус окружности. Ответ: 2.
Слайд 32: Упражнение 36
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:2:3. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 24. Ответ: 9.
Слайд 33: Упражнение 37
Угол между стороной правильного n -угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 72. Найдите n. Ответ: 10.
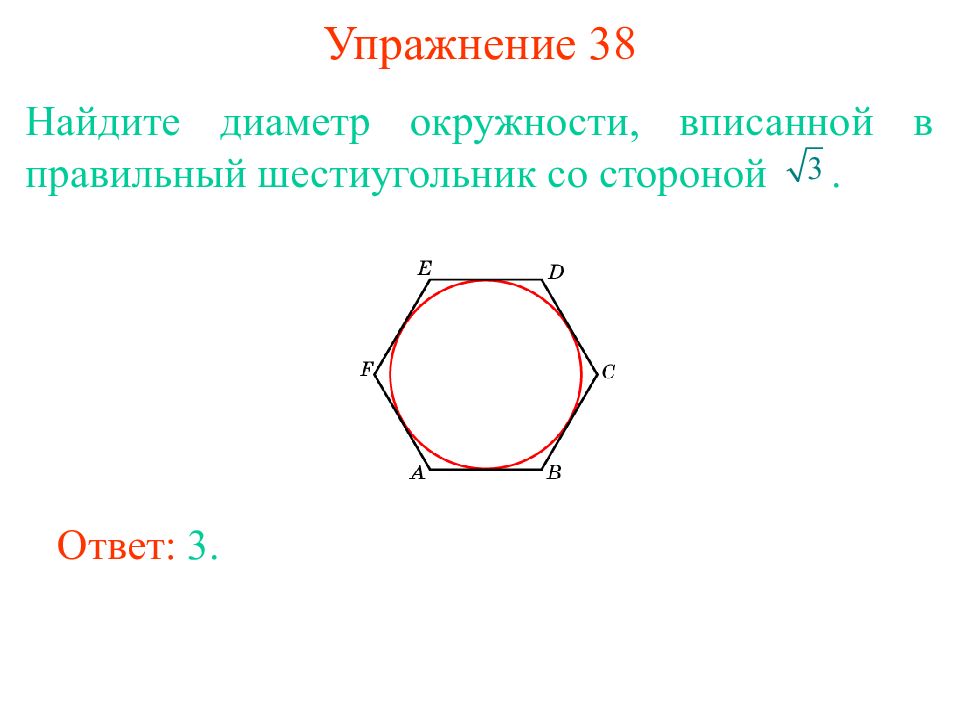
Слайд 34: Упражнение 38
Найдите диаметр окружности, вписанной в правильный шестиугольник со стороной. Ответ: 3.
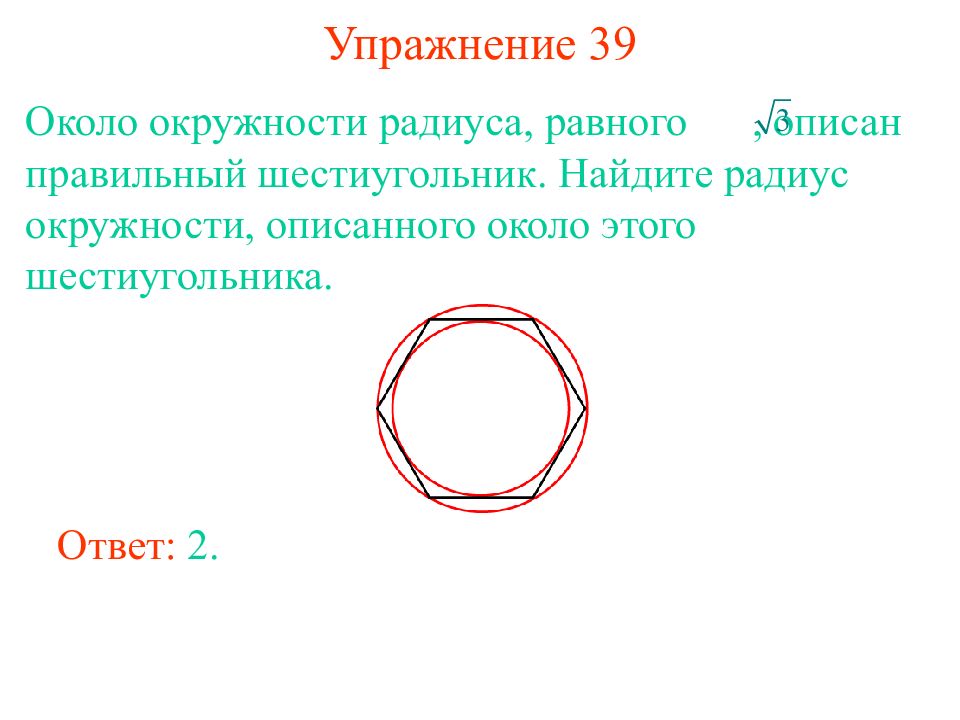
Слайд 35: Упражнение 39
Около окружности радиуса, равного, описан правильный шестиугольник. Найдите радиус окружности, описанного около этого шестиугольника. Ответ: 2.
Слайд 36: Упражнение 40
К окружности, вписанной в треугольник АВС, проведены три касательные. Периметры отсеченных треугольников равны 3, 4, 5. Найдите периметр данного треугольника. Ответ: 12.
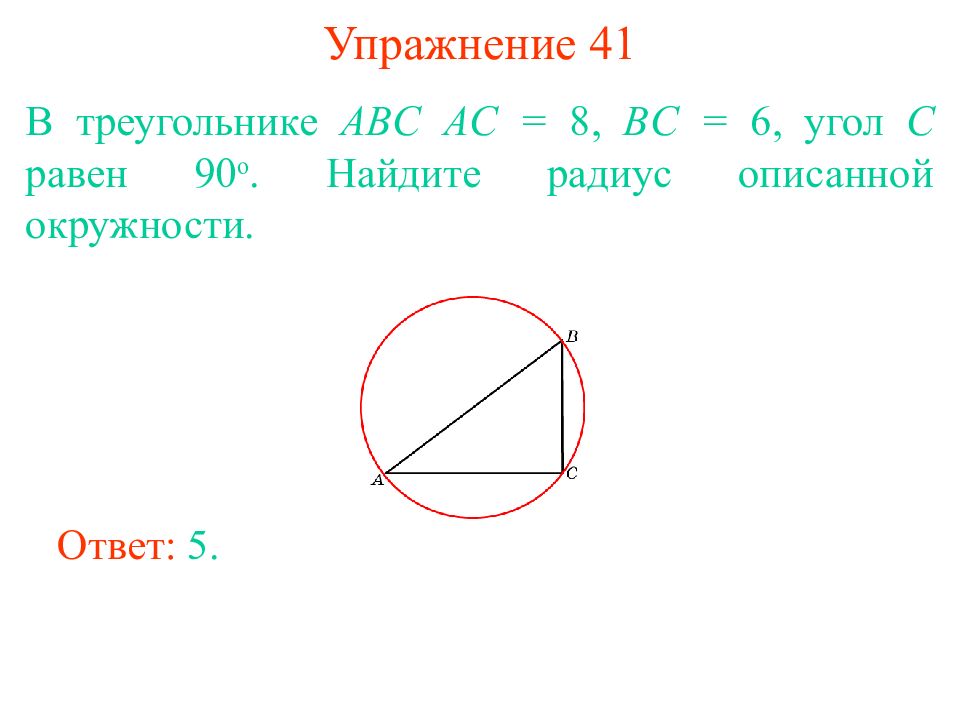
Слайд 37: Упражнение 41
В треугольнике ABC AC = 8, BC = 6, угол C равен 90 о. Найдите радиус описанной окружности. Ответ: 5.
Слайд 38: Упражнение 42
В равнобедренном треугольнике боковые стороны делятся точками касания вписанной в треугольник окружности в отношении 7:5, считая от вершины, противоположной основанию. Найдите периметр треугольника, если его основание равно 10. Ответ: 34.
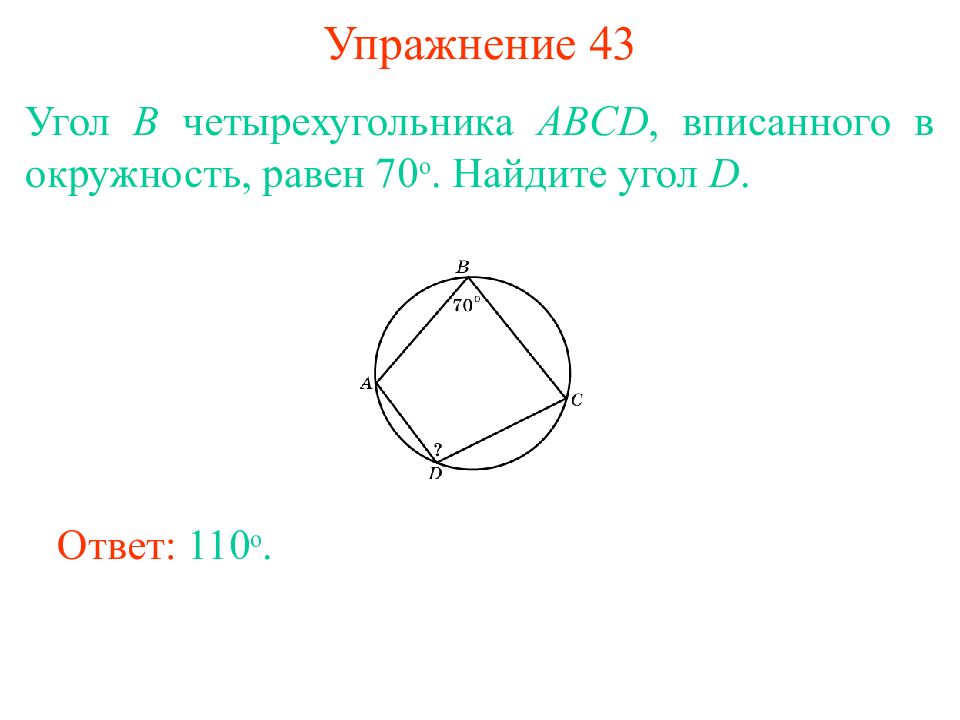
Слайд 39: Упражнение 43
Угол B четырехугольника ABCD, вписанного в окружность, равен 70 о. Найдите угол D. Ответ: 110 о.
Слайд 40: Упражнение 44
Меньшая сторона прямоугольника равна 36. Один из углов, образованных диагоналями 120 о. Найдите диаметр описанной окружности. Ответ: 72.
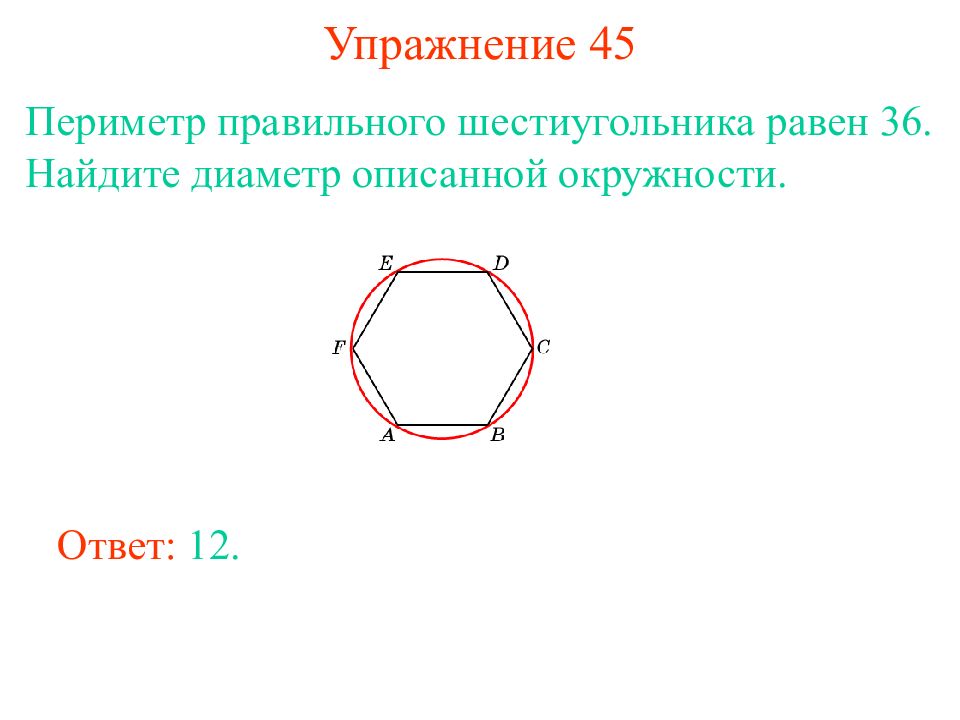
Слайд 41: Упражнение 45
Периметр правильного шестиугольника равен 36. Найдите диаметр описанной окружности. Ответ: 12.
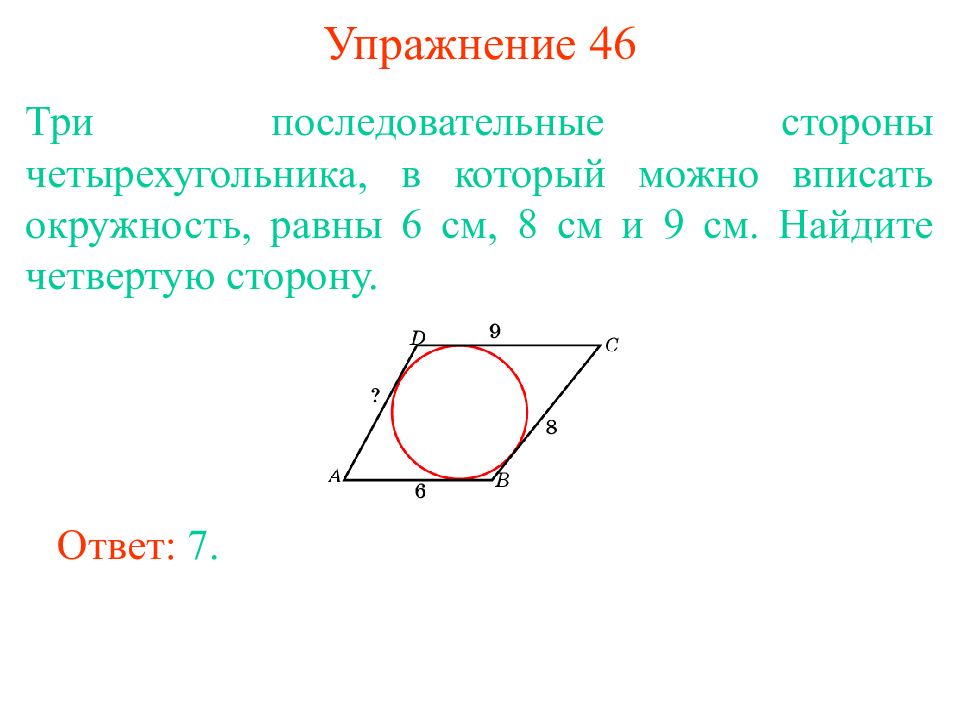
Слайд 42: Упражнение 46
Три последовательные стороны четырехугольника, в который можно вписать окружность, равны 6 см, 8 см и 9 см. Найдите четвертую сторону. Ответ: 7.
Слайд 43: Упражнение 47
Сторона ромба равна 8 см, острый угол – 30 о. Найдите радиус вписанной окружности. Ответ: 2.
Слайд 44: Упражнение 48
Боковые стороны трапеции, описанной около окружности, равны 4 и 6. Найдите среднюю линию трапеции. Ответ: 5.
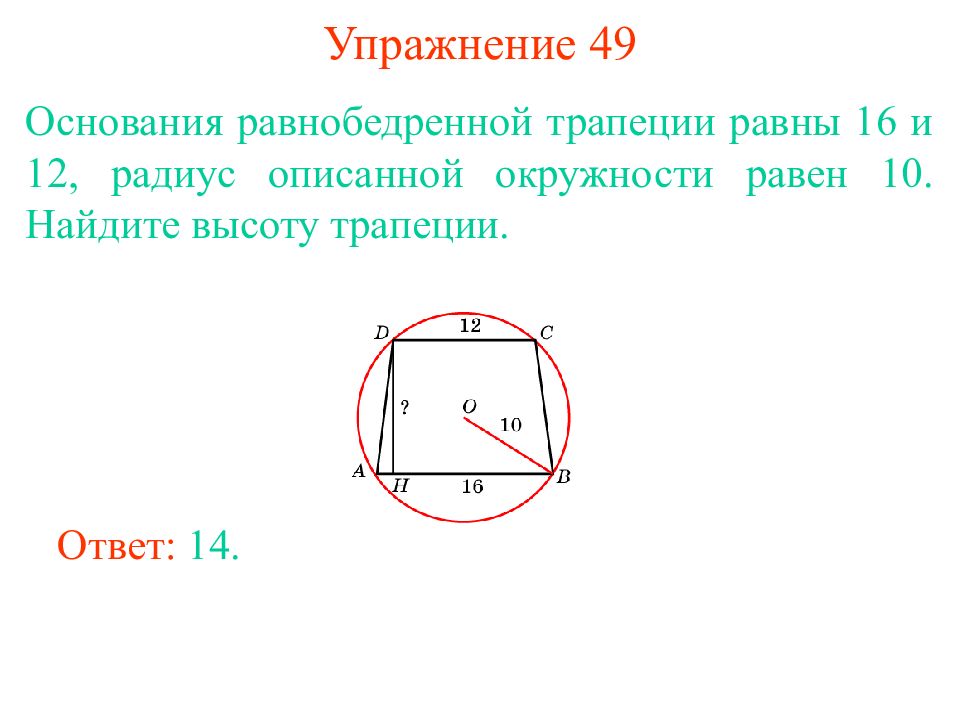
Слайд 45: Упражнение 49
Основания равнобедренной трапеции равны 16 и 12, радиус описанной окружности равен 10. Найдите высоту трапеции. Ответ: 14.