Слайд 3
Содержание лекции № 4 Вязкость. Ньютоновские неньютоновские жидкости Ламинарное и турбулентное течение. Число Рейнольдса Формула Пуазейля Гемодинамика Механические свойства биологических тканей
Слайд 4
Вязкость. Формула Ньютона Вязкость (внутреннее трение) – это свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению слоев. Вязкость возникает из-за внутреннего трения между молекулами жидкости. Река v+dv v dx Между слоями существует градиент скорости скорость сдвига = Течение жидкости по трубе =
Слайд 5
Основной закон вязкого течения был установлен Ньютоном (1713) У равнение Ньютона Формулировка : сила внутреннего трения F между слоями движущейся жидкости прямо пропорциональна скорости сдвига, площади поверхности соприкасающихся слоев S. Коэффициентом пропорциональности является коэффициент вязкости η.
Слайд 6
- напряжение сдвига В реологических характеристиках уравнение Ньютона имеет вид: Напряжение сдвига прямо пропорционально скорости сдвига. η – коэффициент динамической вязкости [ Па ] СИ : [ Па•с ] = паскаль•секунда СГС : [ П ] = пуаз 1 Па•с = 10 П 1мПа•с = 1сП Реология -( rheos – течение, поток ) учение о деформации и текучести вещества.
Слайд 7
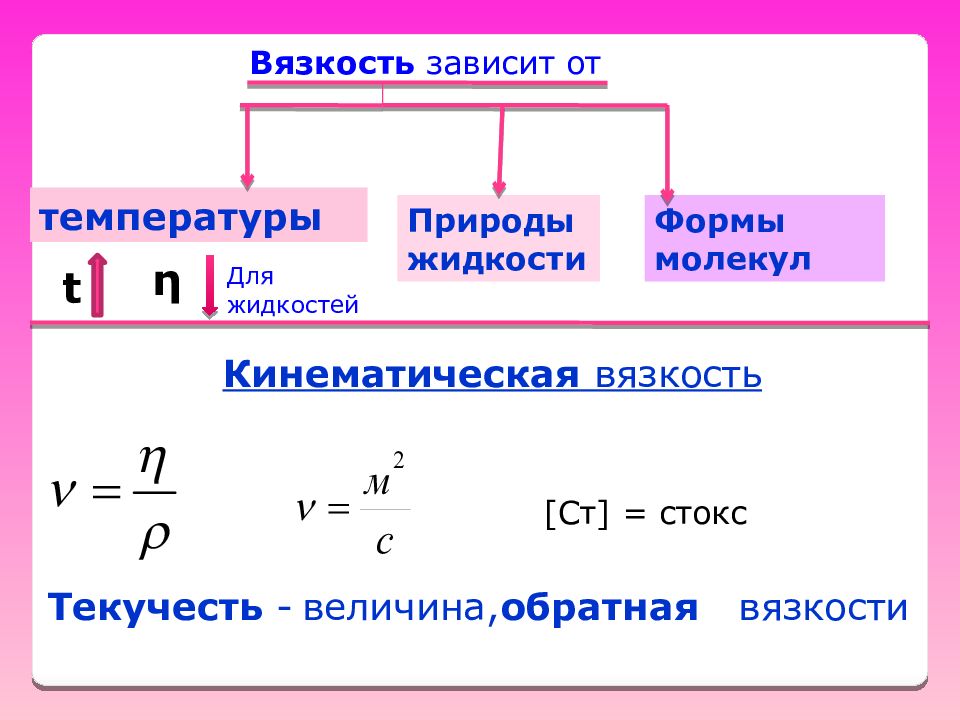
Вязкость зависит от температуры Природы жидкости Формы молекул Кинематическая вязкость [ Ст ] = стокс Текучесть - величина, обратная вязкости t η Для жидкостей
Слайд 8
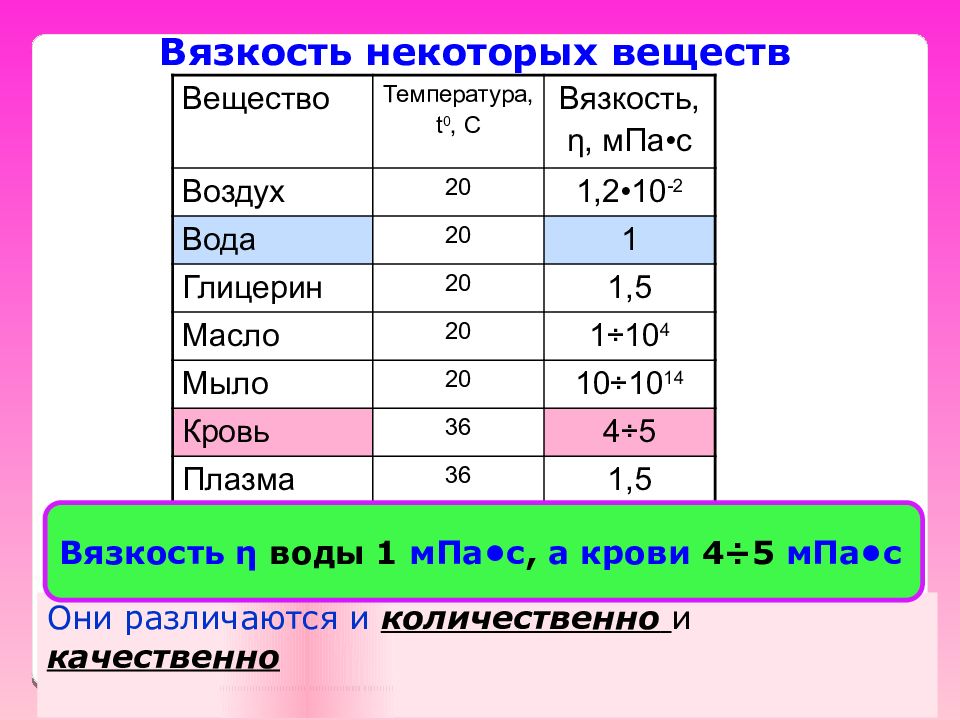
Вещество Температура, t 0, C Вязкость, η, мПа•с Воздух 20 1,2 •10 -2 Вода 20 1 Глицерин 20 1,5 Масло 20 1 ÷ 10 4 Мыло 20 10 ÷ 10 14 Кровь 36 4 ÷ 5 Плазма 36 1,5 Вязкость некоторых веществ Они различаются и количественно и качественно Вязкость η воды 1 мПа•с, а крови 4 ÷ 5 мПа•с
Слайд 9
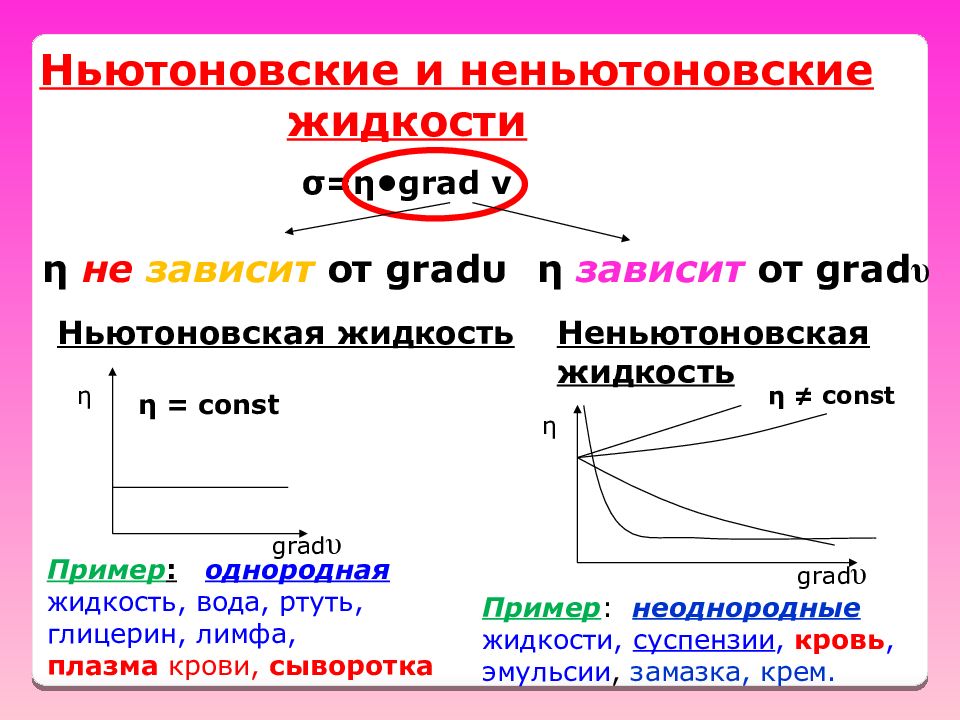
Ньютоновские и неньютоновские жидкости Ньютоновская жидкость σ = η• grad ν Неньютоновская жидкость η = const grad υ η не зависит от grad υ η η зависит от grad υ Пример : однородная жидкость, вода, ртуть, глицерин, лимфа, плазма крови, сыворотка η ≠ const grad υ η Пример : неоднородные жидкости, суспензии, кровь, эмульсии, замазка, крем.
Слайд 10
Кровь как неньютоновская жидкость Кровь = плазма + форменные элементы Кровь является нень ютоновской жидкостью, так как это суспензия форменных элементов в белковом растворе. Вязкость η крови 4 ÷ 5 мПа•с ВОПРОС: Каких форменных элементов? Эритроцитов. ПОЧЕМУ эритроцитов? Эритроциты составляют 93%
Слайд 11
Вязкость крови зависит от режима течения. Чем медленнее течет кровь, тем выше вязкость η grad υ Зависимость вязкости крови от режима течения В капиллярах grad v ↓ η ↑ η = 800 мПа•с В артериях grad v ↑ η ↓ η = 4-5 мПа•с При низких скоростях сдвига эритроциты образуют «монетные столбики» При высоких скоростях сдвига вязкость крови определяется 1) Концентрацией эритроцитов 2 ) Их физическими свойствами.
Слайд 12
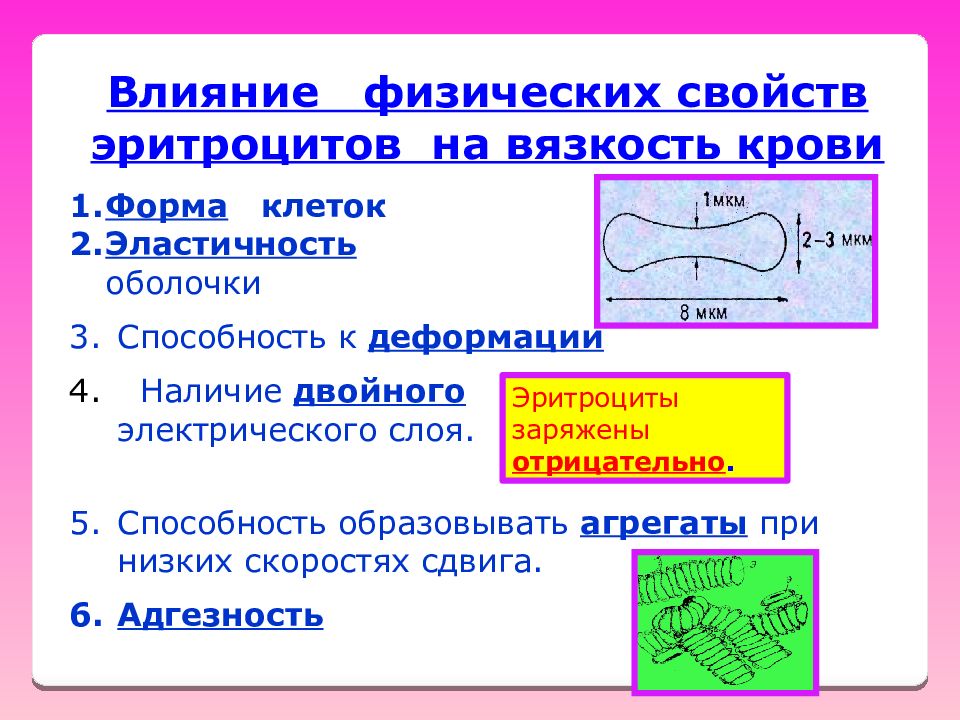
Влияние физических свойств эритроцитов на вязкость крови Форма клеток Эластичность оболочки Способность к деформации Наличие двойного электрического слоя. Способность образовывать агрегаты при низких скоростях сдвига. Адгезность Эритроциты заряжены отрицательно.
Слайд 13
Сыворотка – это плазма без фибриногена η =1,1мПа • с Плазма крови – водно-солевой белковый раствор. Плазма – ньютоновская жидкость. η =1,2мПа•с Эта цифра вязкости при 37 0 С. Что с ней произойдет при повышении температуры до 41 0 С ? Вопрос : Понизится на 10%
Слайд 14
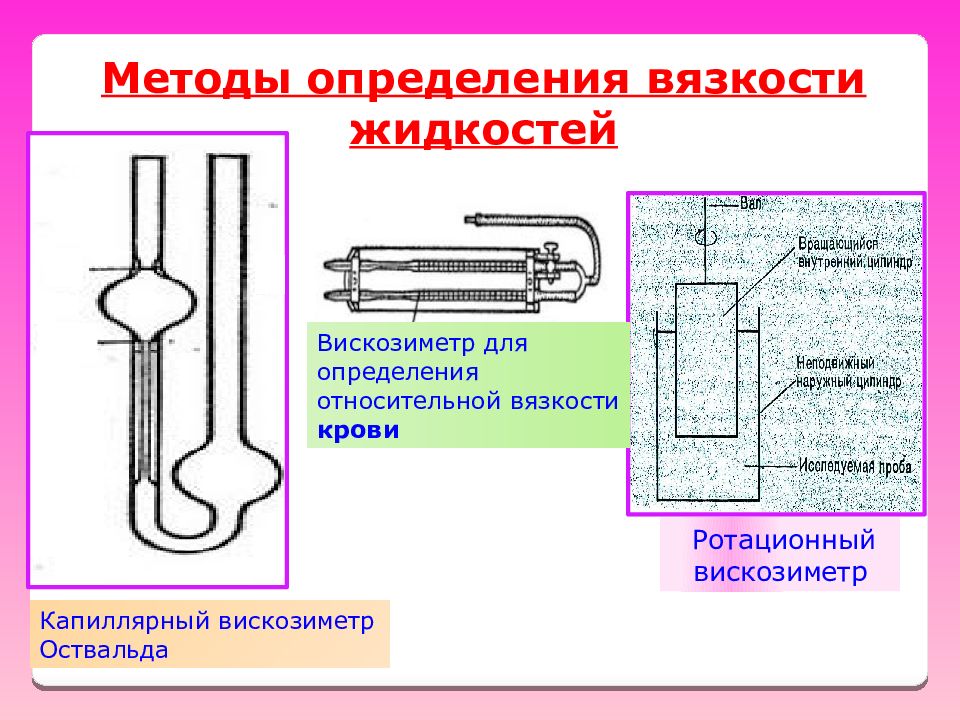
Методы определения вязкости жидкостей Капиллярный вискозиметр Оствальда Ротационный вискозиметр Вискозиметр для определения относительной вязкости крови
Слайд 15
Вискозиметр VT550 - высокоточная модель с широким диапазоном измерения, ручной или автоматический режим под управлением компьютера. Ротационный вискозиметр Rheotest RV2.1 Наиболее простая модель ротационного вискозиметра, Устройство работает без применения персонального компьютера, имеет аналоговый дисплей и выход на самописец. Экспресс-анализатор- вискозиметр ротационный
Слайд 16
Стационарный поток Стационарный поток это такой поток, когда через каждый уровень поперечного сечения, протекает одинаковый объем жидкости Условие стационарности потока Q=const Q - объемная скорость – это объем жидкости, протекающий через поперечное сечение за единицу времени.
Слайд 17
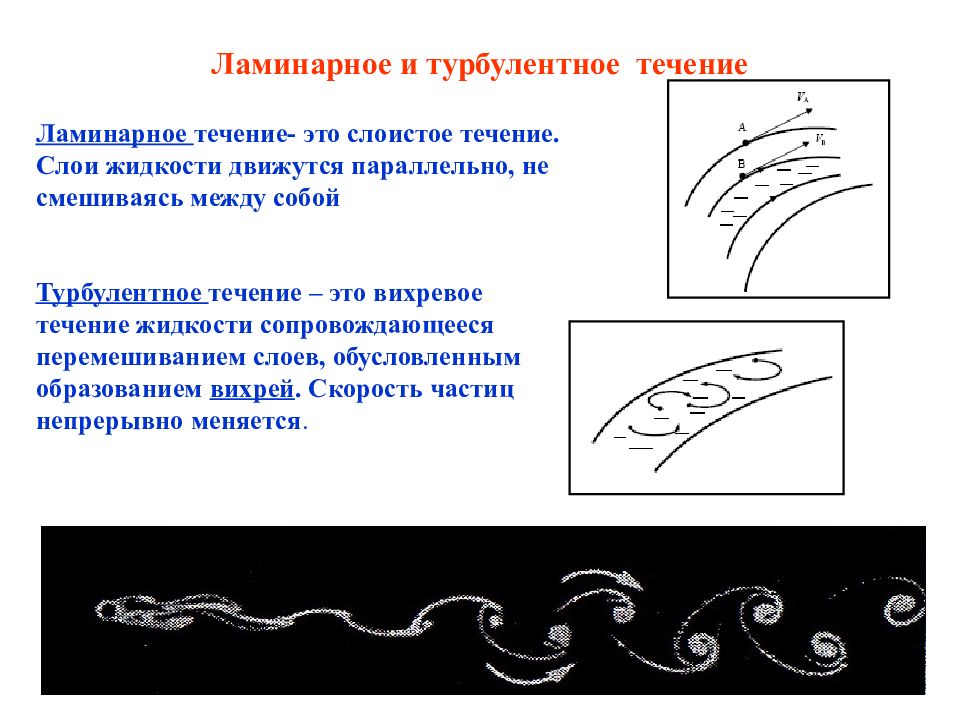
Ламинарное и турбулентное течения Ламинарное течение- это слоистое течение. Слои жидкости движутся параллельно, не смешиваясь между собой Турбулентное течение – это вихревое течение - жидкости сопровождающееся перемешиванием слоев, обусловленным образованием вихрей. Скорость частиц непрерывно меняется.
Слайд 18
Характер течения жидкости определяется числом Рейнольдса РЕЙНОЛЬДС, ОСБОРН (1842–1912), Л аминарное течение переходит в турбулентное, когда введенное им число Рейнольдса превышает критическое значение. Величина безразмерная Если Re < Re кр = > Ламинарное течение Если Re > Re кр = ˃ Турбулентное течение Re крит. ( H 2 O) = 2300 Re крит. ( кровь ) = 970 ± 80. ρ - плотность; v – скорость; d- диаметр сосуда: η - вязкость
Слайд 19
Re – критерий подобия двух потоков: Два потока считаются тождественными, если равны числа Рейнольдса. Физический смысл числа Рейнольдса : Re ( капилляры ) <<1 R e = 10 -3 - мало ( вязкость ↑ ) Re ( артерии ) >>1 Вязкость инерция ↑ ν V
Слайд 20
Формула Пуазейля Пуазейл ь Жан Мари французский врач + физик + физиолог Преподавал медицинскую физику Пуазейль 1799-1869
Слайд 21
Формулировка: Объём жидкости Q, протекающей по горизонтальной трубе небольшого сечения за единицу времени, прямо пропорционален радиусу трубы R в четвёртой степени, разности давлений ∆ P на концах трубы, обратно пропорционален коэффициенту вязкости η и длине трубы ι. Коэффициентом пропорциональности является π /8 (получен эмпирически ).
Слайд 22
Гидравлическое сопротивление = > Основное уравнение гемодинамики Перепад д авлений прямо пропорционален гидравлическому сопротивлению
Слайд 23
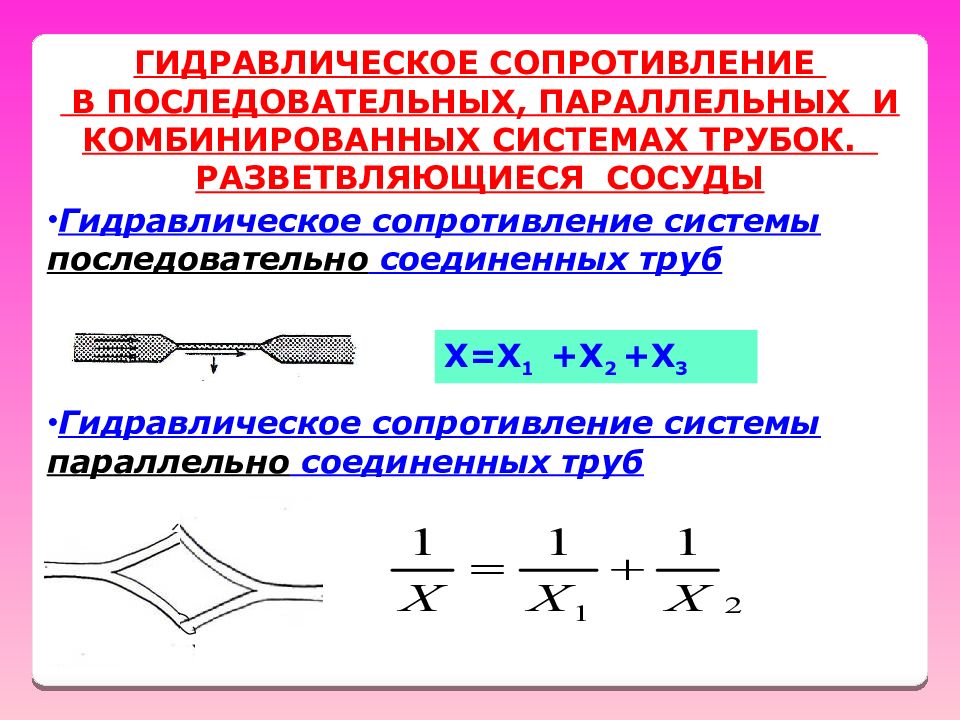
ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ В ПОСЛЕДОВАТЕЛЬНЫХ, ПАРАЛЛЕЛЬНЫХ И КОМБИНИРОВАННЫХ СИСТЕМАХ ТРУБОК. РАЗВЕТВЛЯЮЩИЕСЯ СОСУДЫ Гидравлическое сопротивление системы последовательно соединенных труб Х=Х 1 +Х 2 +Х 3 Гидравлическое сопротивление системы параллельно соединенных труб
Слайд 24
Сужение сосуда Скорость потока возрастает Сопротивление увеличивается S ٠ υ = const ↑ ∆ P=Q ٠ x ↑ Перепад давлений увеличивается
Слайд 25
Расширение сосуда Скорость потока уменьшается Сопротивление падает Перепад давлений уменьшается S ٠ υ = const ∆ P=Q ٠ x
Слайд 26
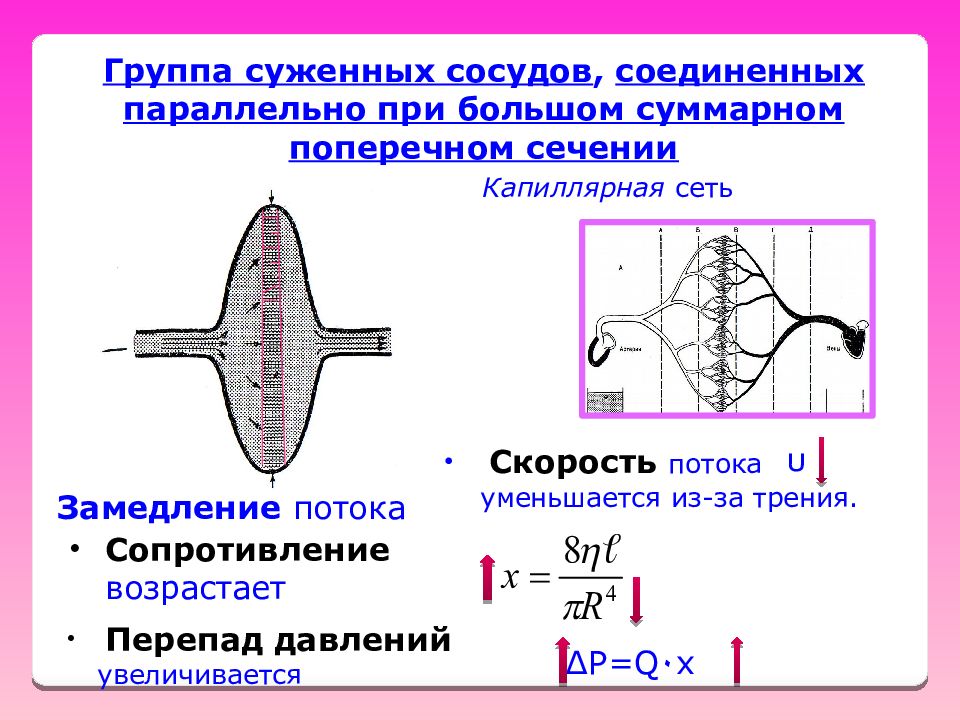
Группа суженных сосудов, соединенных параллельно при большом суммарном поперечном сечении Замедление потока Скорость потока уменьшается из-за трения. Сопротивление возрастает υ Перепад давлений увеличивается ∆ P=Q ٠ x Капиллярная сеть
Слайд 27
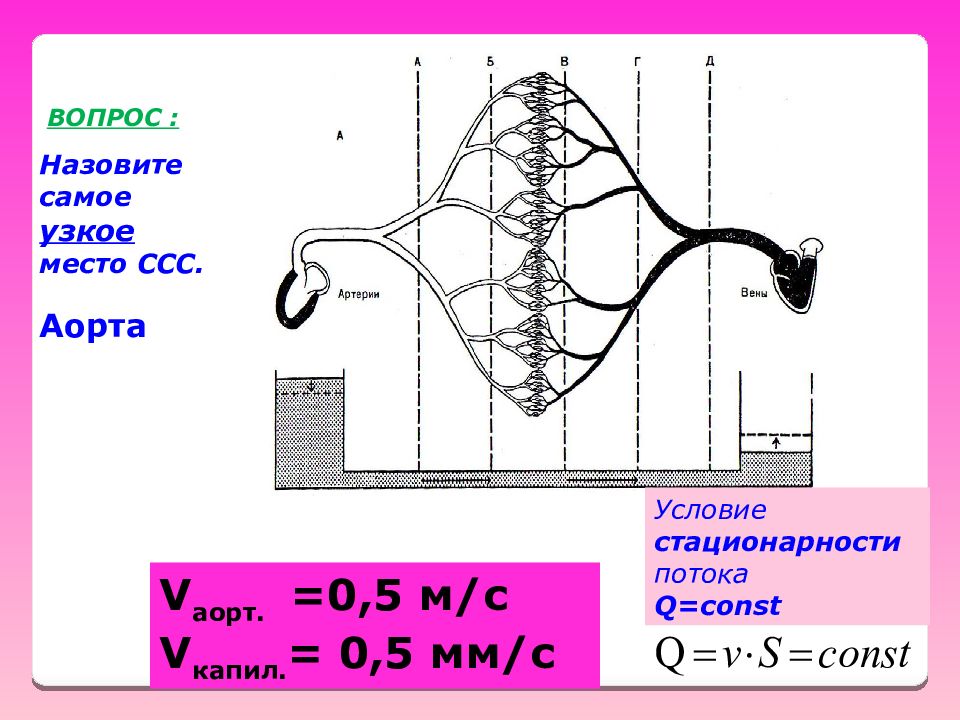
V аорт. =0,5 м / с V капил. = 0,5 мм / с ВОПРОС : Аорта Назовите самое узкое место ССС. Условие стационарности потока Q=const
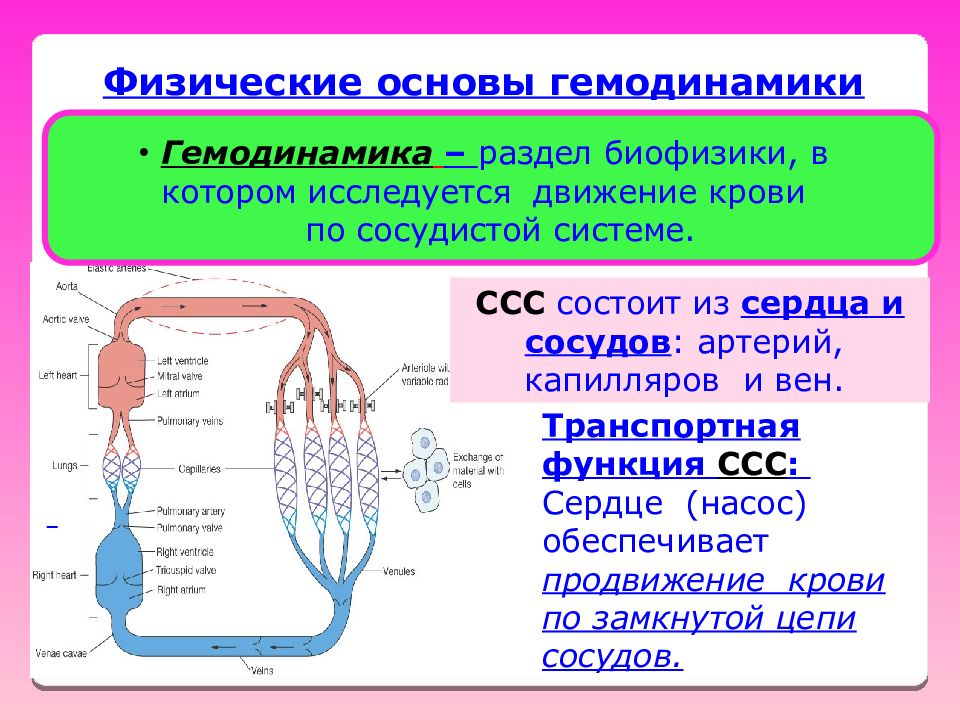
Слайд 28
Транспортная функция ССС : Сердце (насос) обеспечивает продвижение крови по замкнутой цепи сосудов. Физические основы гемодинамики Гемодинамика – раздел биофизики, в котором исследуется движение крови по сосудистой системе. ССС состоит из сердца и сосудов : артерий, капилляров и вен.
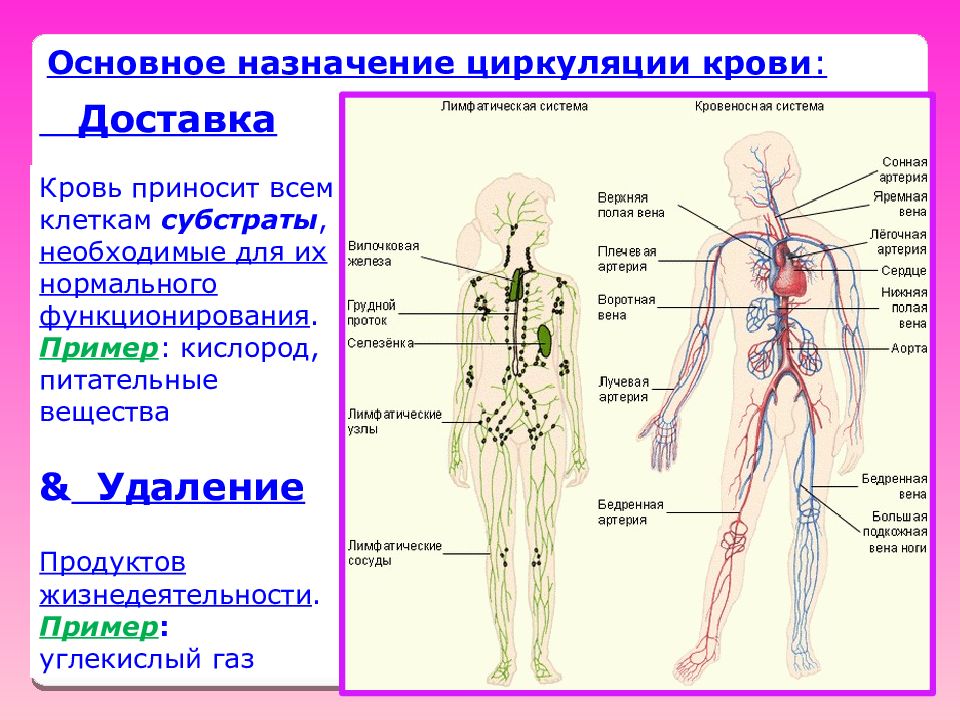
Слайд 29
Основное назначение циркуляции крови : Доставка Кровь приносит всем клеткам субстраты, необходимые для их нормального функционирования. Пример : кислород, питательные вещества & Удаление Продуктов жизнедеятельности. Пример : углекислый газ
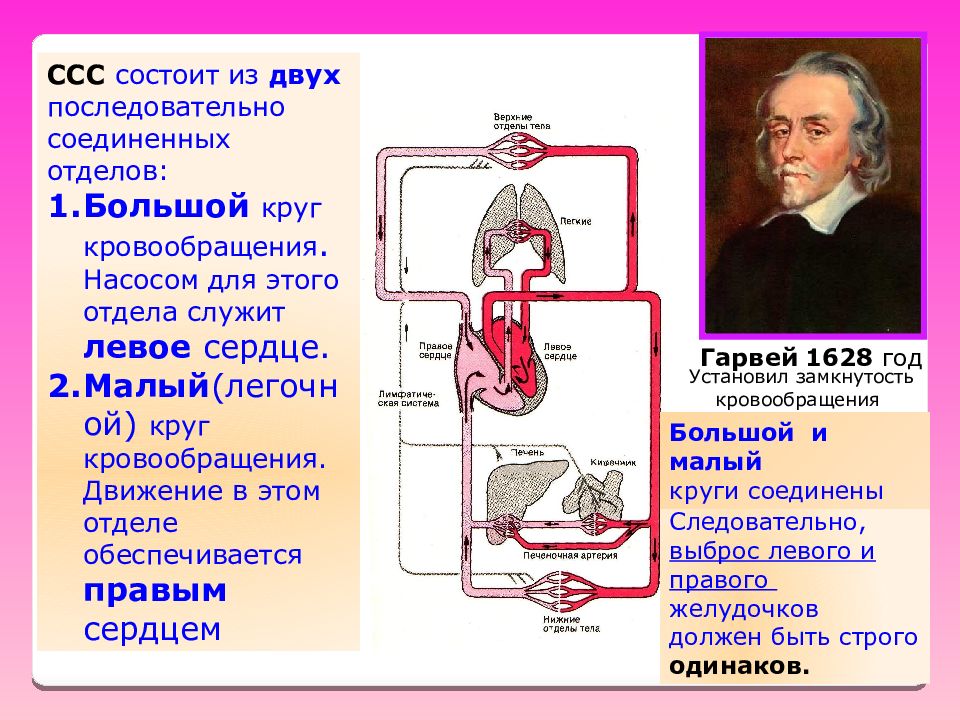
Слайд 30
ССС состоит из двух последовательно соединенных отделов: Большой круг кровообращения. Насосом для этого отдела служит левое сердце. Малый (легочной) круг кровообращения. Движение в этом отделе обеспечивается правым сердцем последовательно Следовательно, выброс левого и правого желудочков должен быть строго одинаков. Гарвей 1628 год Большой и малый круги соединены Установил замкнутость кровообращения
Слайд 31
Ударный объем крови Это объем крови, который выталкивается из сердца за одно сокращение V уд равен 600 мл 6 л Столовая ложка 15 г 6 мл 60 мл Ответ: 60 мл ВОПРОС:
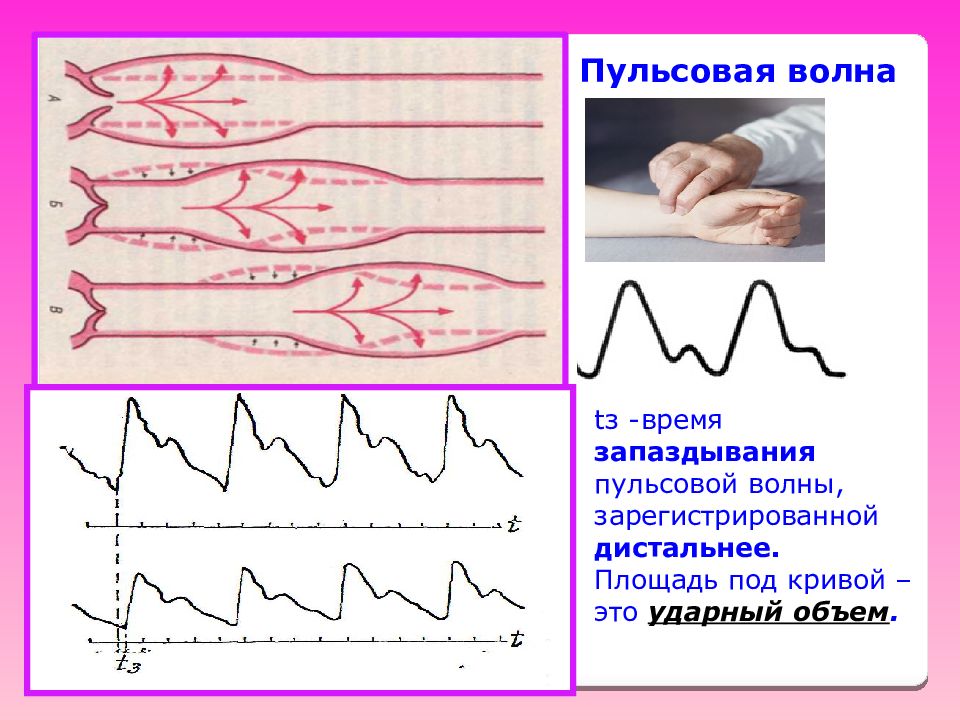
Слайд 32
Пульсовая волна, скорость ее распространения Пульсовая волна - это волна деформации стенок артерии. Пульсовая волна – это распространяющаяся по аорте и артериям волна повышенного давления, вызванная выбросом крови из левого желудочка в аорту в период систолы. Причина : упругость аортальной стенки В китайской литературе пульс сравнивают с плавающей по воде шелковой тканью.
Слайд 33
t з - время запаздывания пульсовой волны, зарегистрированной дистальнее. Площадь под кривой – это ударный объем. Пульсовая волна
Слайд 34
СРПВ – количественный показатель упругих свойств артерии. Формула Моенса - Кортевега Скорость распространения пульсовой волны v Е –модуль Юнга h- толщина стенки d – диаметр сосуда ρ – плотность крови В норме 5-10 м/с. Что происходит с СРПВ с возрастом? Она увеличивается
Слайд 35
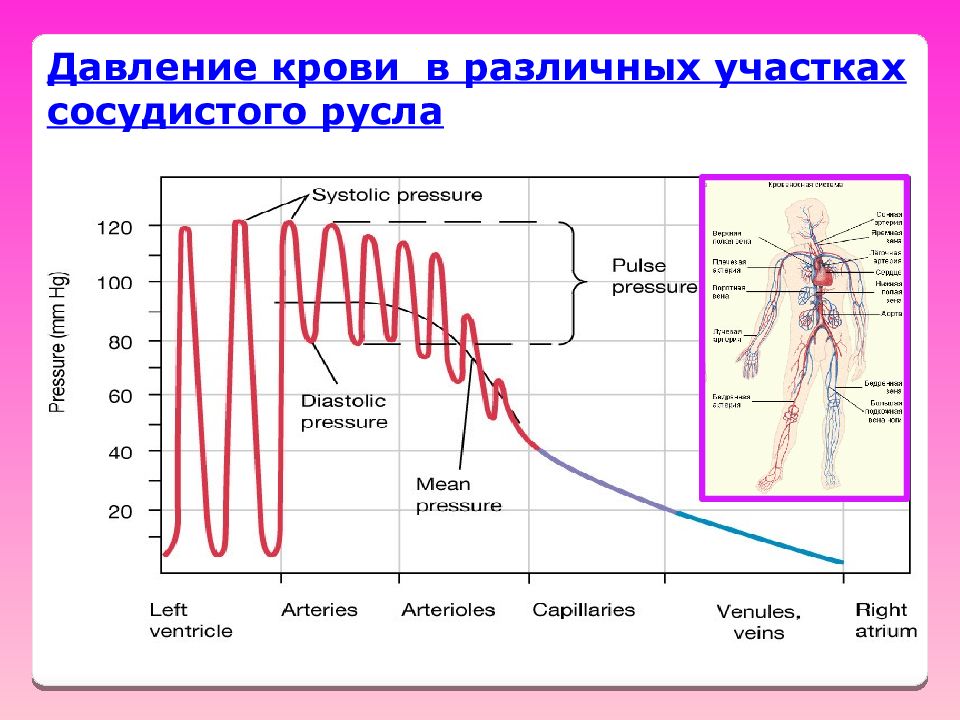
Давление крови в артериях колеблется от максимального во время сокращения сердца (систолы) до минимального во время расслабления (диастолы). При каждом сердцебиении давление крови поднимается до систолического уровня, а между ударами падает до диастолического уровня Поэтому артериальное давление определяют как максимальное / минимальное значения ( систолическое / диастолическое ). Обычно его измеряют в миллиметрах ртутного столба. В норме 120 / 80 мм рт.ст. для здоровых взрослых людей. ВОПРОС: А в комнате 760 мм рт.ст. – в 5 раз больше, и мы живы. Катакрота Анакрота
Слайд 36
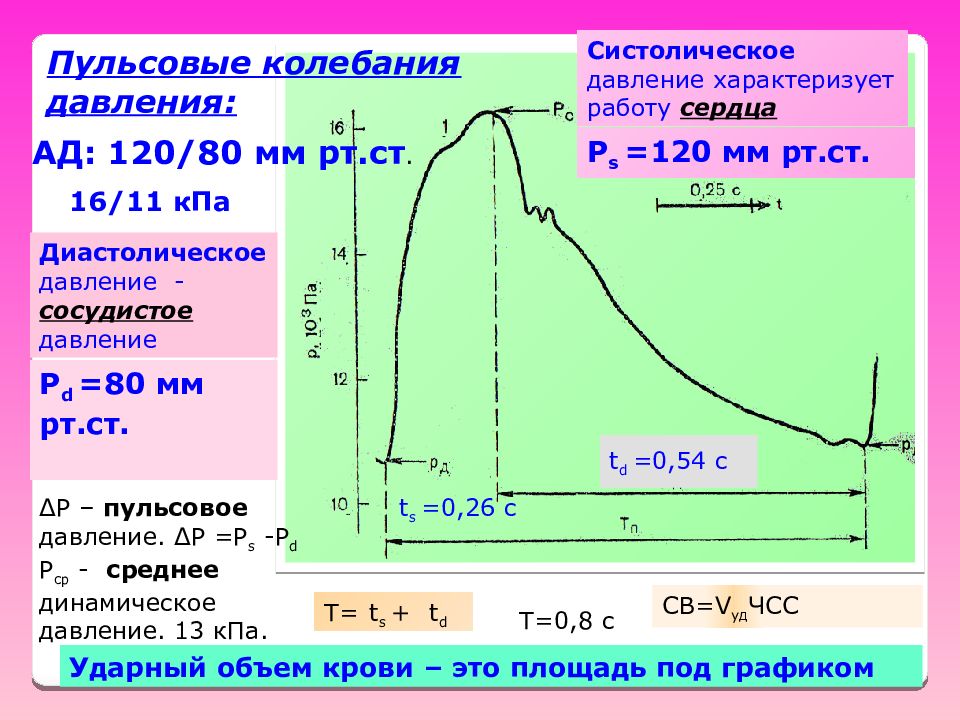
АД: 120 / 80 мм рт.ст. 16 / 11 кПа Систолическое давление характеризует работу сердца Диастолическое давление - сосудистое давление P s =120 мм рт.ст. P d =80 мм рт.ст. t s =0,26 с t d =0,54 с T= t s + t d T= 0,8 с СВ= V уд ЧСС Ударный объем крови – это площадь под графиком ΔР – пульсовое давление. ΔР = P s - P d Р ср - среднее динамическое давление. 13 кПа. Пульсовые колебания давления:
Слайд 38
СФИГМОМАНОМЕТР = = Манжета +груша + манометр Физические основы клинического метода измерения давления крови. Основан на измерении внешнего давления, необходимого, чтобы пережать артерию.
Слайд 39
Сфигмоманометр ртутный Сфигмоманометр UA-101, имитирует ртутный тонометр
Слайд 40
Метод Короткова по измерению АД 105-ЛЕТИЕ НАУЧНОГО ОТКРЫТИЯ ХИРУРГА ВОЕННО-МЕДИЦИНСКОЙ АКАДЕМИИ Н.С.КОРОТКОВА, СДЕЛАВШЕГО ЭПОХУ В РАЗВИТИИ МИРОВОЙ МЕДИЦИНЫ В созвездии имен великих медиков, заслуживших благодарность всего человечества за свои открытия в медицине, нашло свое место имя русского врача Н. С. Короткова. 8 ноября 1905 года Коротков (ему был 31 год ) в своем докладе на «Научном Совещании Клинического военного госпиталя Военно-медицинской академии» сообщил об открытом им звуковом методе бескровного определения максимального и минимального артериального давления (АД) у человека. Korotkoff’s method.
Слайд 41
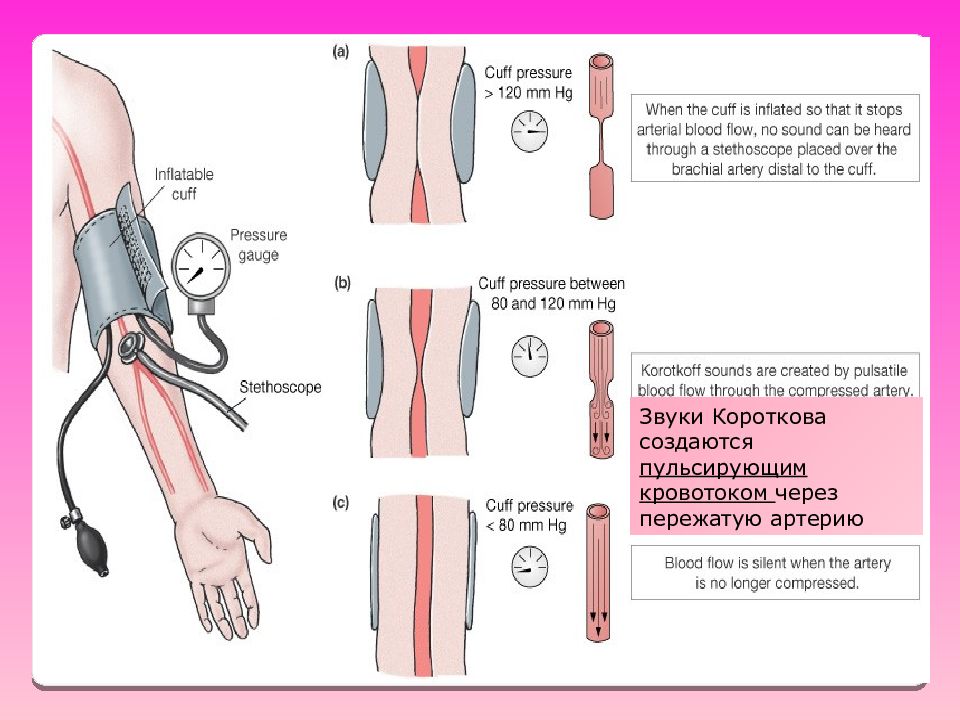
Измерение артериального давления методом Короткова ( аускультативный метод) Основан на возникновении турбулентного течения, когда давление в манжете станет равным систолическому давлению.
Слайд 42
Звуки Короткова создаются пульсирующим кровотоком через пережатую артерию
Слайд 43
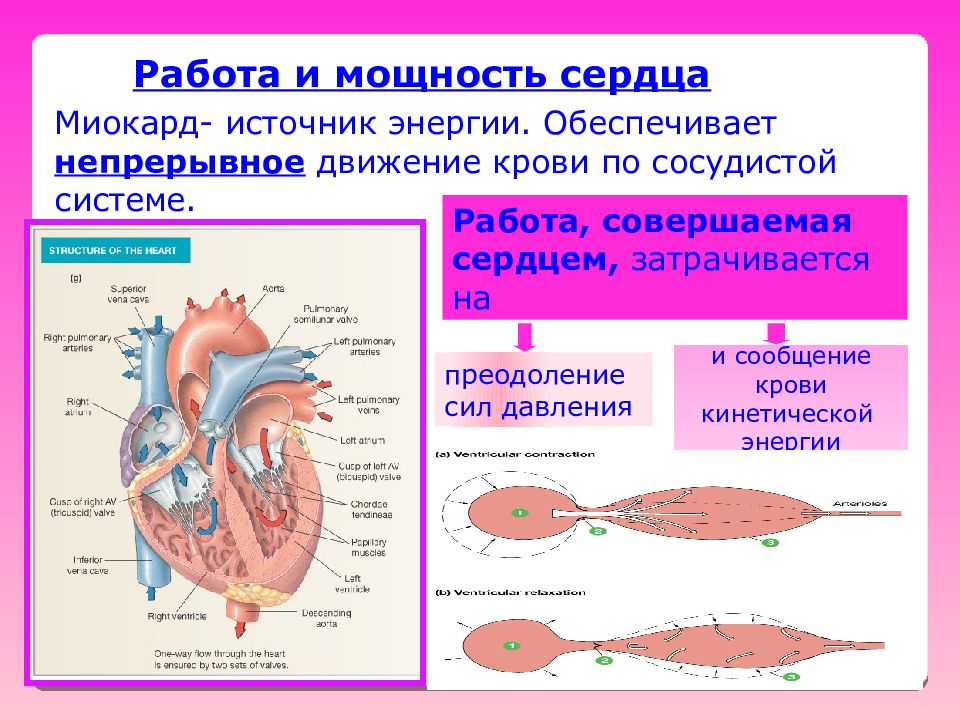
Работа и мощность сердца Миокард- источник энергии. Обеспечивает непрерывное движение крови по сосудистой системе. Работа, совершаемая сердцем, затрачивается на преодоление сил давления и сообщение крови кинетической энергии
Слайд 44
Работа левого желудочка Работа правого желудочка А пр = 0,2 А лев. Всего: Работа сердца равна Р – среднее динамическое давление. 13 кПа V – ударный объем крови. 70 мл Плотность крови 1050 кг / м 3 -скорость кровотока 0,5 м / с
Слайд 45
Мощность сердца Больше или меньше мощность сердца, чем мощность электробритвы ? ОТВЕТ: 12 Вт
Слайд 46
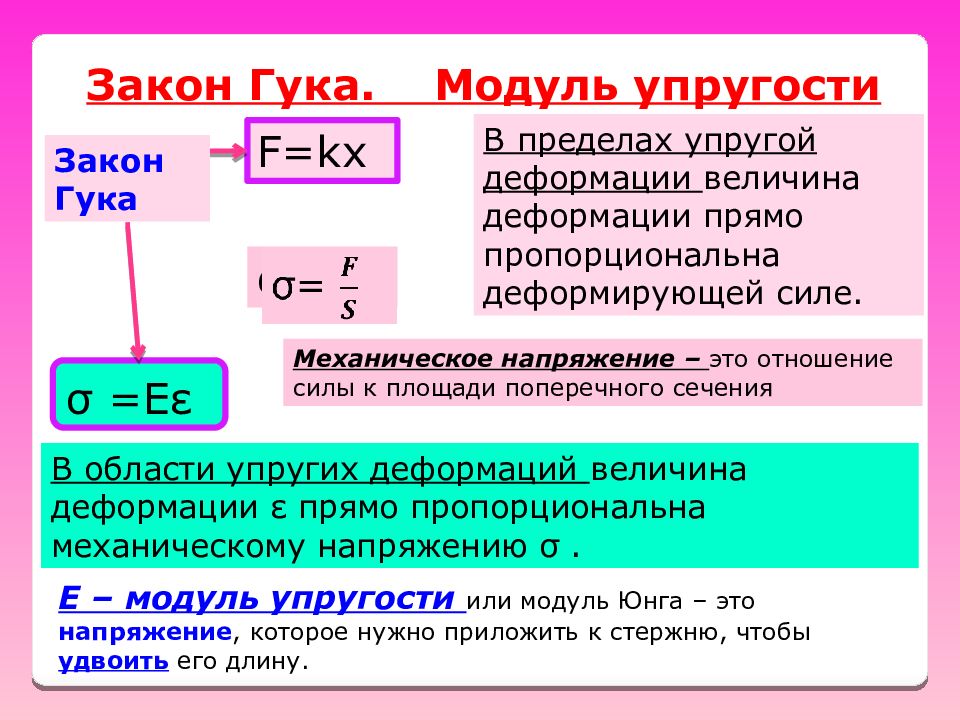
Закон Гука. Модуль упругости Закон Гука σ =Е ε В пределах упругой деформации величина деформации прямо пропорциональна деформирующей силе. F= kx σ = Механическое напряжение – это отношение силы к площади поперечного сечения В области упругих деформаций величина деформации ε прямо пропорциональна механическому напряжению σ. Е – модуль упругости или модуль Юнга – это напряжение, которое нужно приложить к стержню, чтобы удвоить его длину.
Слайд 47
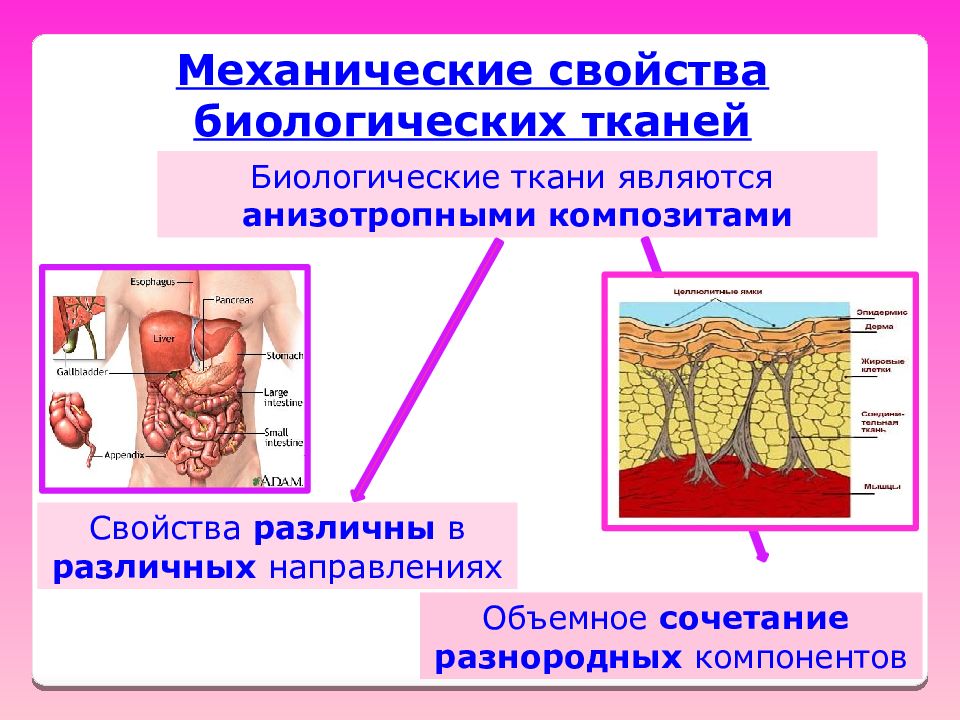
Механические свойства биологических тканей Биологические ткани являются анизотропными композитами Свойства различны в различных направлениях Объемное сочетание разнородных компонентов
Слайд 48
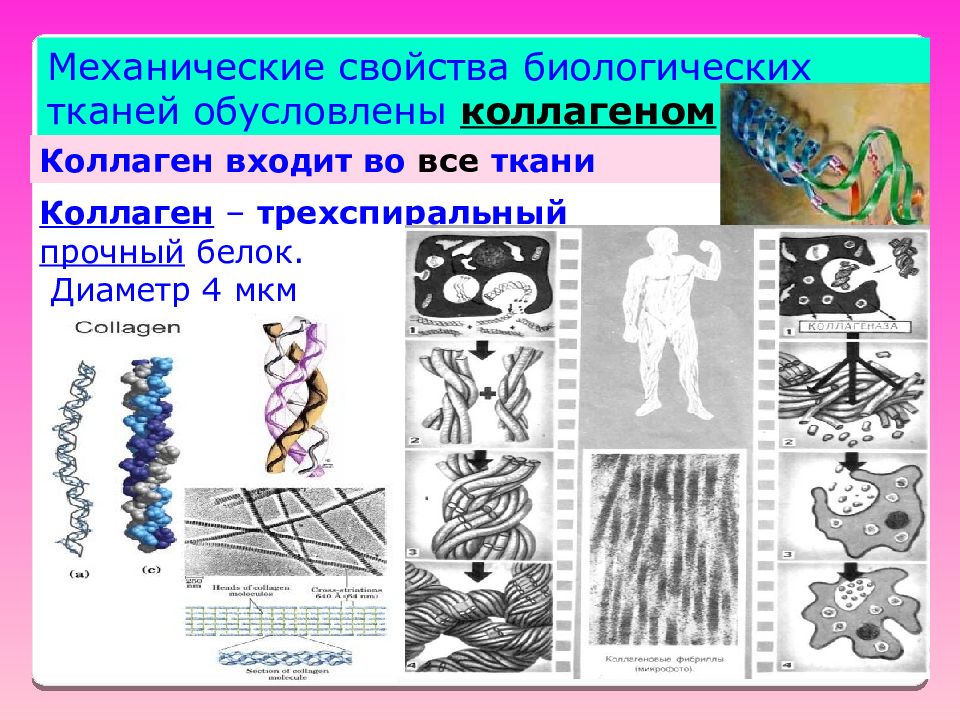
Механические свойства биологических тканей обусловлены коллагеном Коллаген – трехспиральный прочный белок. Диаметр 4 мкм Коллаген входит во все ткани
Слайд 49
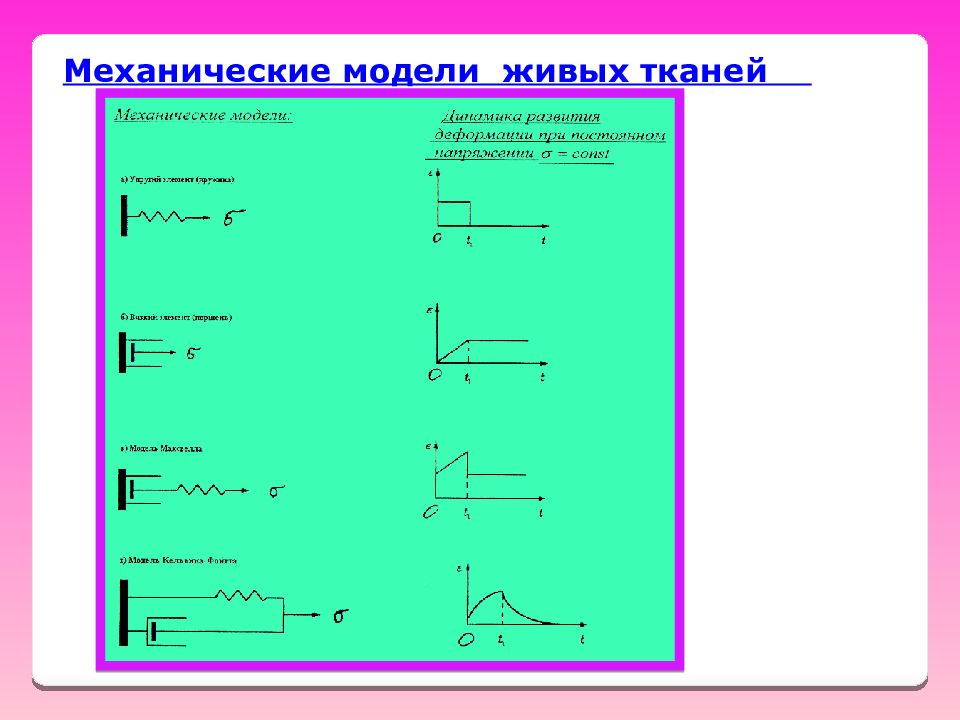
Механические свойства биологических тканей Это вязко - упругие и упруго -вязкие системы Прочность Модуль Юнга не постоянен Пластичность Противостояние механической усталости Нелинейная зависимость напряжение-деформация
Слайд 50
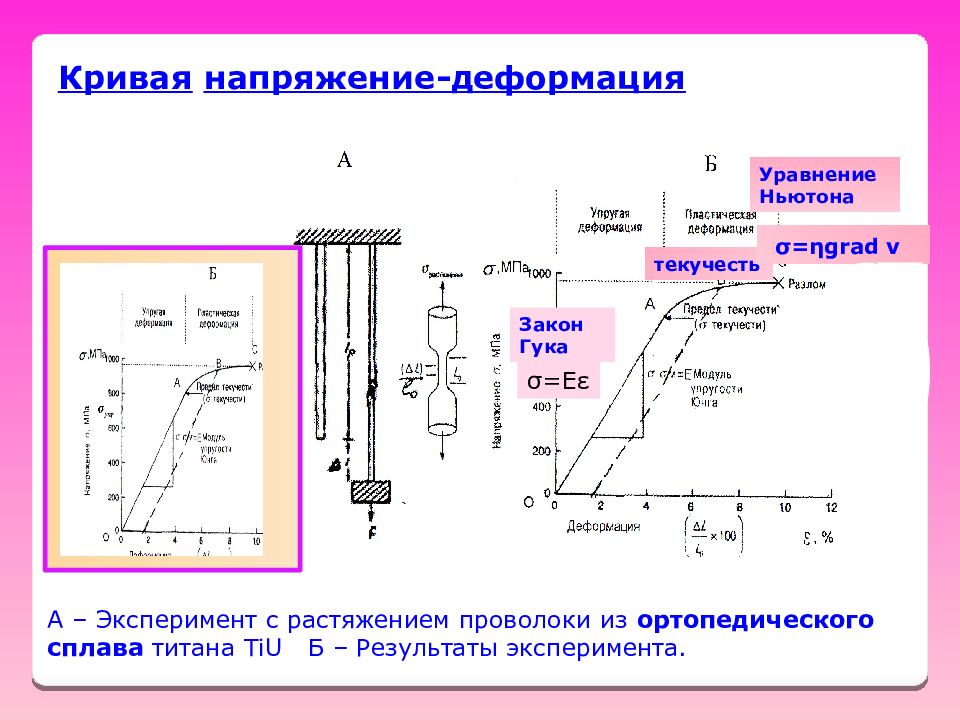
Кривая напряжение-деформация Кривая напряжение-деформация A – Эксперимент с растяжением проволоки из ортопедического сплава титана TiU Б – Результаты эксперимента. Закон Гука σ =Е ε текучесть Уравнение Ньютона σ = η grad v
Слайд 52
Упругие и прочностные свойства костной ткани Это твёрдое упругое тело. ρ =2,4 ٠ 10 3 кг/м 3 1/3 коллаген (орг.) 2/3 гидроксиапатит ( неорг.) Минеральные соли Ca, P Волокнистая структура коллагеновой матрицы пронизана игольчатыми кристаллами гидроксиапатита. Там кальций. Он держит воду. Кость гидрофильна. Роль коллагена : Придает вязкость.
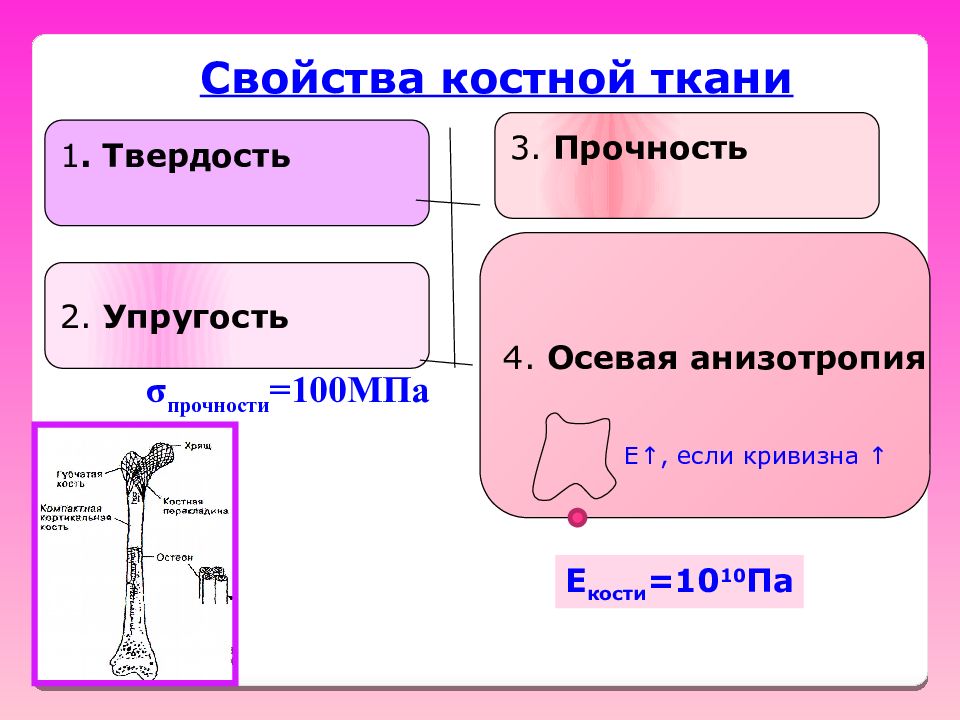
Слайд 53
Свойства костной ткани 1. Твердость 2. Упругость 3. Прочность 4. Осевая анизотропия E ↑, если кривизна ↑ σ прочности =100МПа E кости =10 10 Па
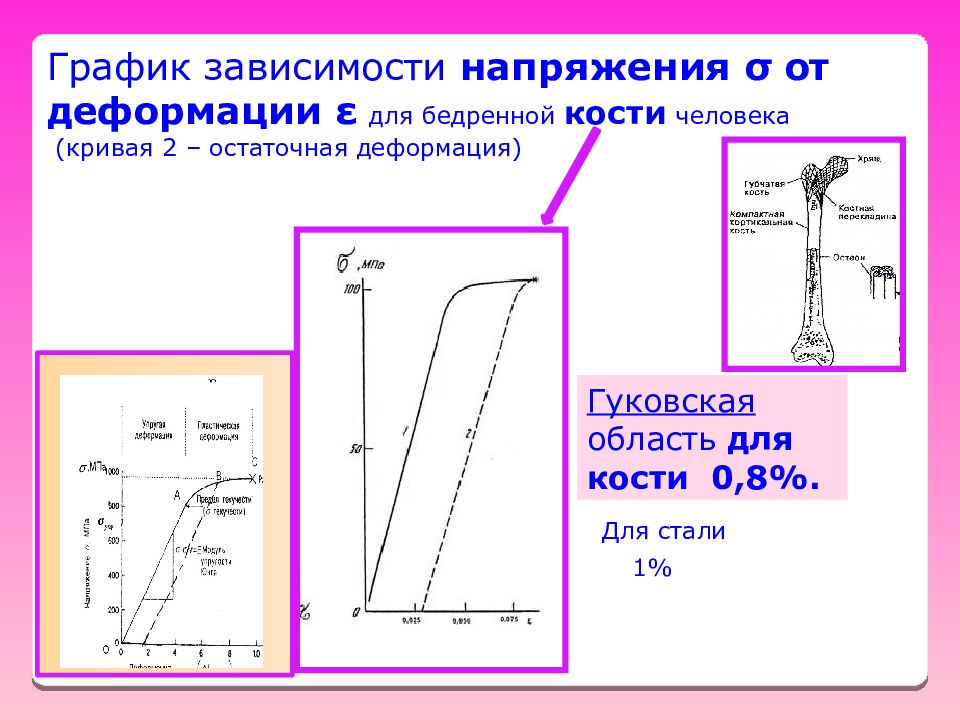
Слайд 54
График зависимости напряжения σ от деформации ε для бедренной кости человека (кривая 2 – остаточная деформация) Гуковская область для кости 0,8%. Для стали 1%
Слайд 55
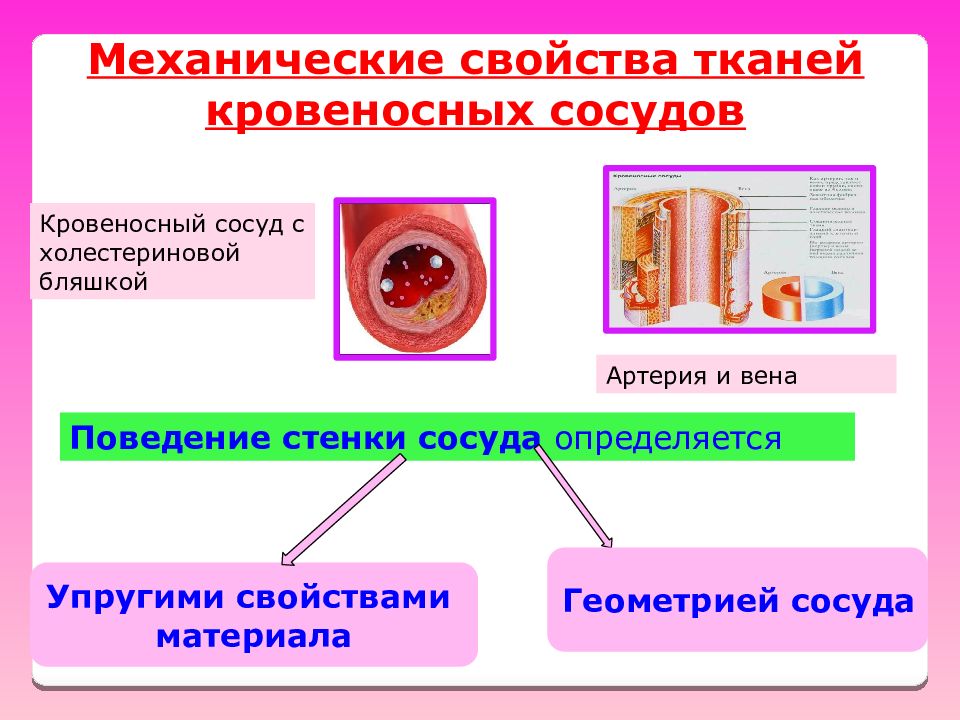
Поведение стенки сосуда определяется Упругими свойствами материала Геометрией сосуда Механические свойства тканей кровеносных сосудов Кровеносный сосуд с холестериновой бляшкой Артерия и вена
Слайд 56
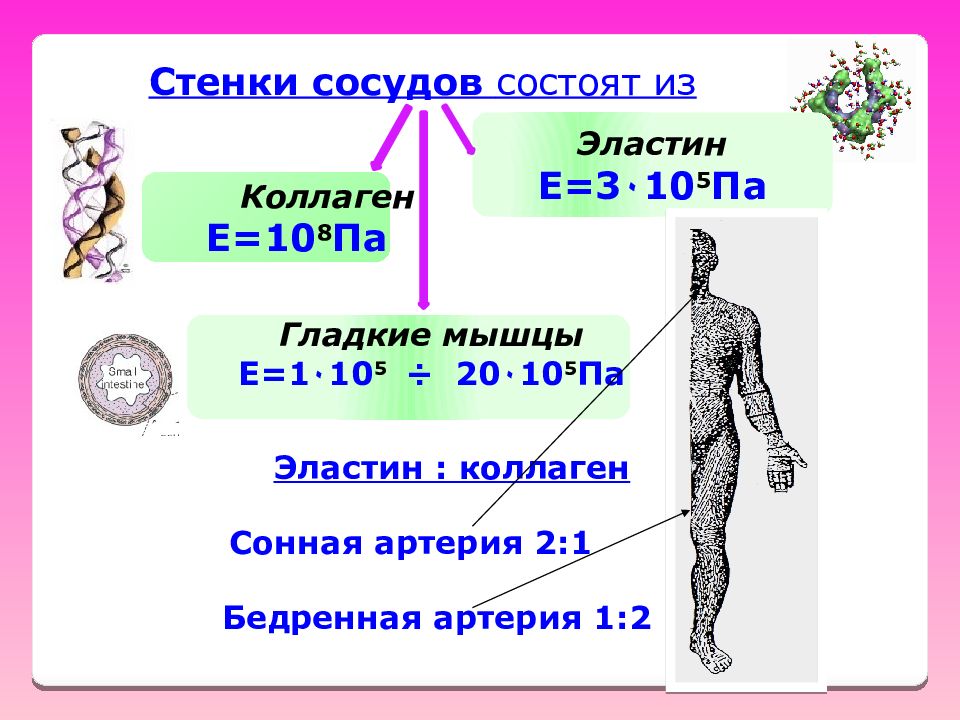
Стенки сосудов состоят из Коллаген Е=10 8 Па Эластин Е=3 ٠ 10 5 Па Гладкие мышцы Е=1 ٠ 10 5 ÷ 20 ٠ 10 5 Па Эластин : коллаген Сонная артерия 2:1 Бедренная артерия 1:2
Слайд 57
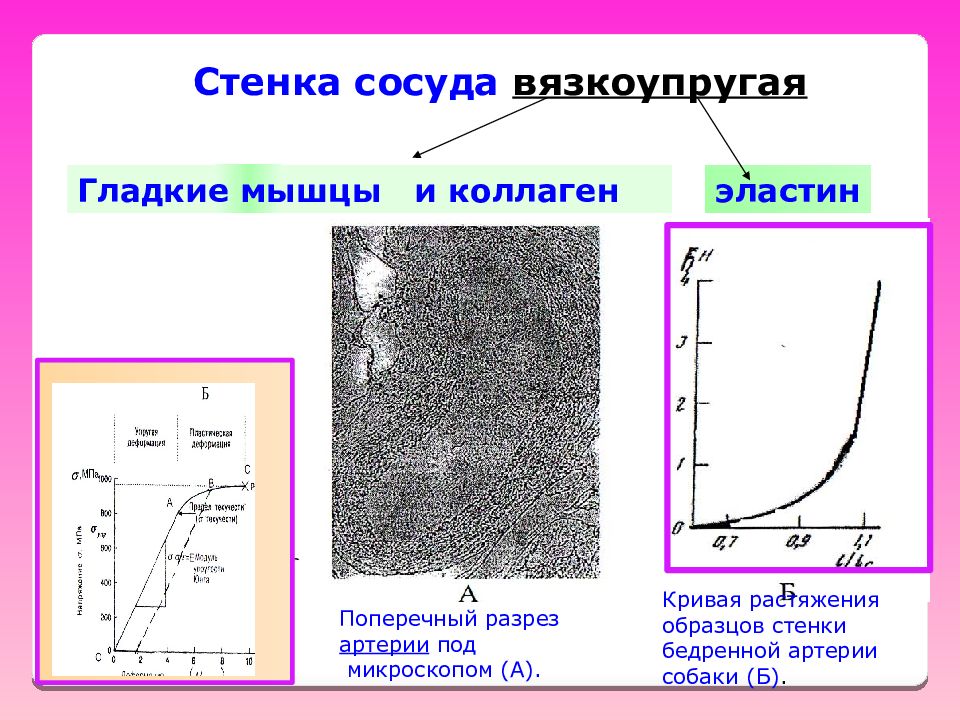
Стенка сосуда вязкоупругая Гладкие мышцы и коллаген эластин Поперечный разрез артерии под микроскопом (А). Кривая растяжения образцов стенки бедренной артерии собаки (Б).
Слайд 58
Геометрия сосуда Фрагменты сосуда А – Продольный; Б – вид с торца; В – формы, которые может принимать спавшийся исходно круглый сосуд - Уравнение Ламе P – внутрисосудистое давление; r – радиус сосуда; σ – механическое напряжение; h – толщина стенки.