Первый слайд презентации: Курс медицинской и биологической физики для медико-профилактического факультет а
ЛЕКЦИЯ 2. Физические основы гидродинамики идеальной и вязкой жидкости. Физические основы гемодинамики Белорусский государственный медицинский университет Кафедра медицинской и биологической физики 1
Слайд 2
Гидродинамика – это раздел физики, изучающий законы движения и силы взаимодействия в жидкостях.
Слайд 3
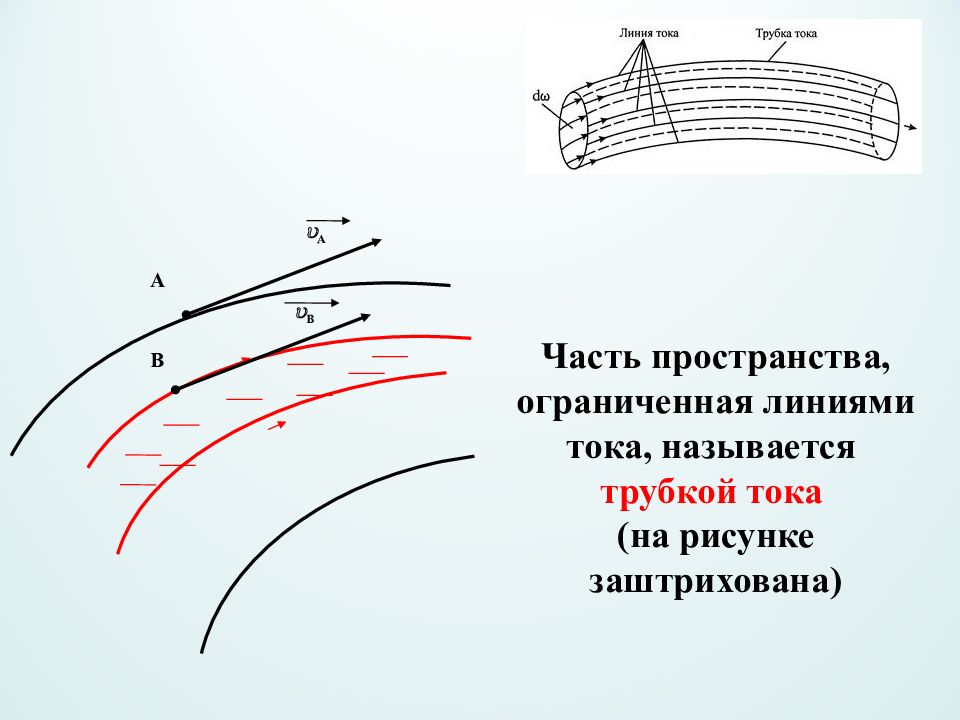
Основные понятия и законы гидродинамики Течение жидкости характеризуется линиями тока. Это линии, касательные к которым совпадают с направлением вектора скорости частиц жидкости в данной точке 1 2 Идеальной называют абсолютно невязкую и несжимаемую жидкость
Слайд 4
Часть пространства, ограниченная линиями тока, называется трубкой тока (на рисунке заштрихована) В А A B
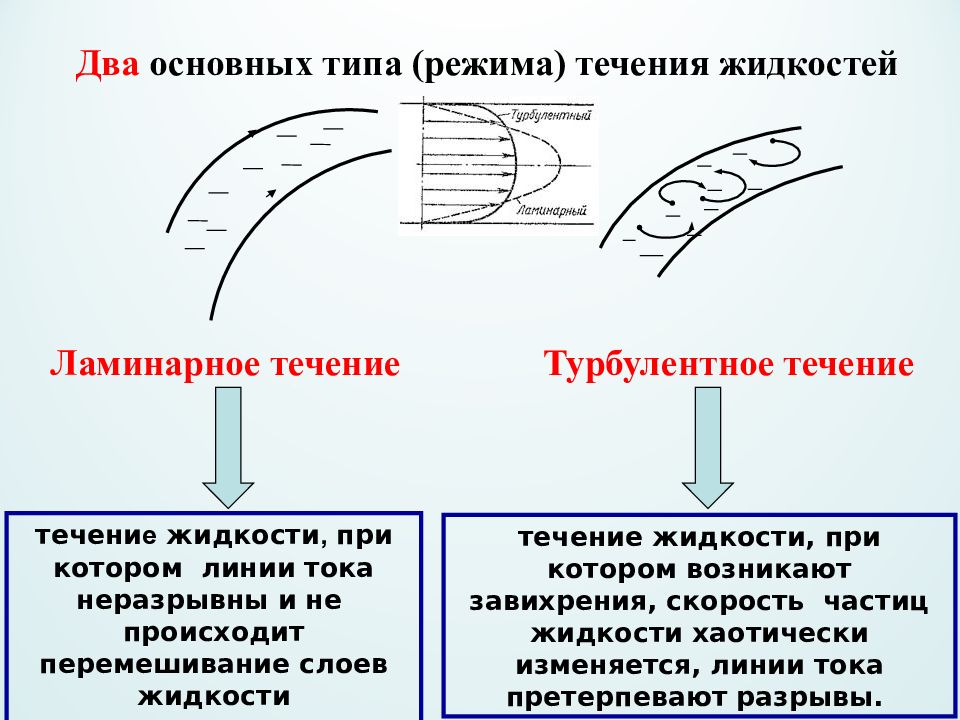
течени е жидкости, при котором линии тока неразрывны и не происходит перемешивание слоев жидкости течение жидкости, при котором возникают завихрения, скорость частиц жидкости хаотически изменяется, линии тока претерпевают разрывы. Ламинарное течение Турбулентное течение
Слайд 6
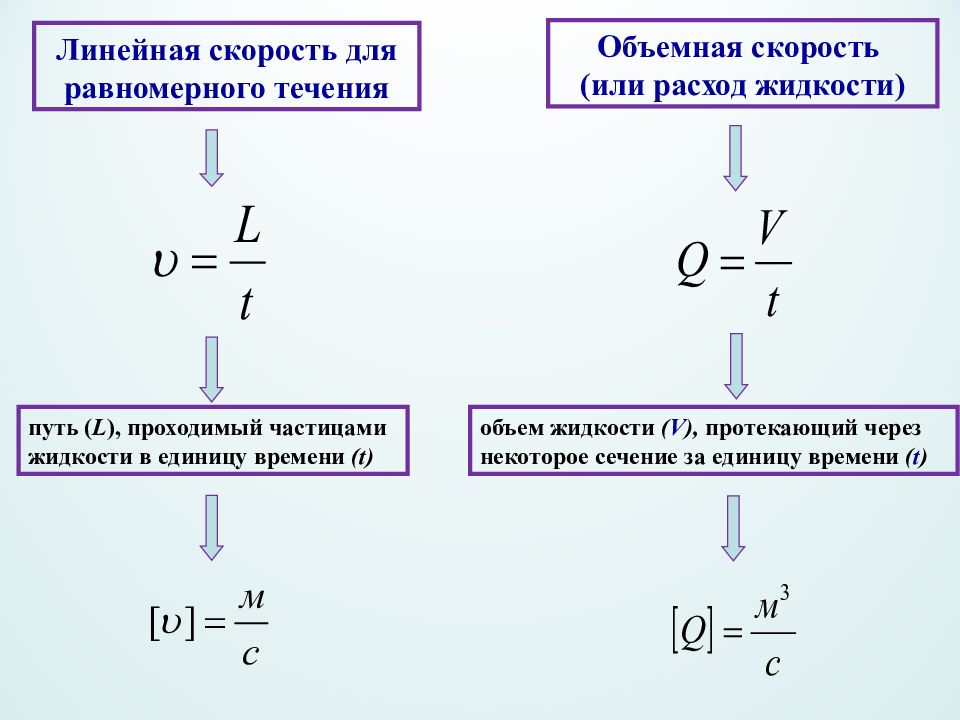
Линейная скорость для равномерного течения путь ( L ), проходимый частицами жидкости в единицу времени ( t) Объемная скорость (или расход жидкости) объем жидкости ( V ), протекающий через некоторое сечение за единицу времени ( t )
Слайд 7
Связь между линейной и объемной Q скоростью течения жидкости S – площадь поперечного сечения трубы L – длина трубы
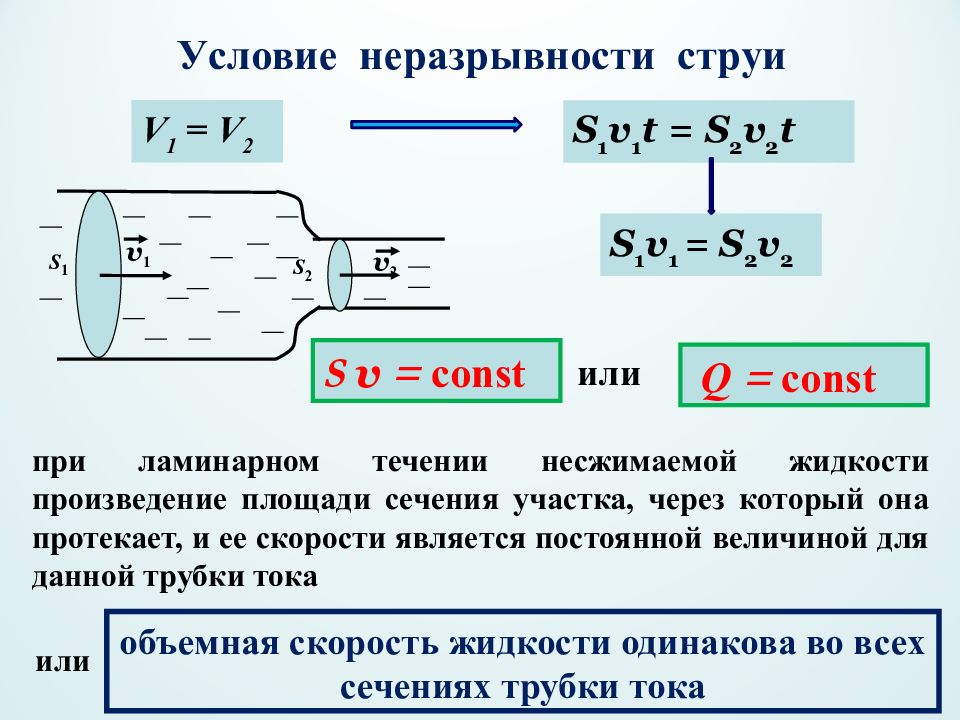
Слайд 8: У словие неразрывности струи
S v = const при ламинарном течении несжимаемой жидкости произведение площади сечения участка, через который она протекает, и ее скорости является постоянной величиной для данной трубки тока S 1 v 1 S 2 v 2 S 1 v 1 = S 2 v 2 V 1 = V 2 S 1 v 1 t = S 2 v 2 t Q = const или объемная скорость жидкости одинакова во всех сечениях трубки тока или
Слайд 9
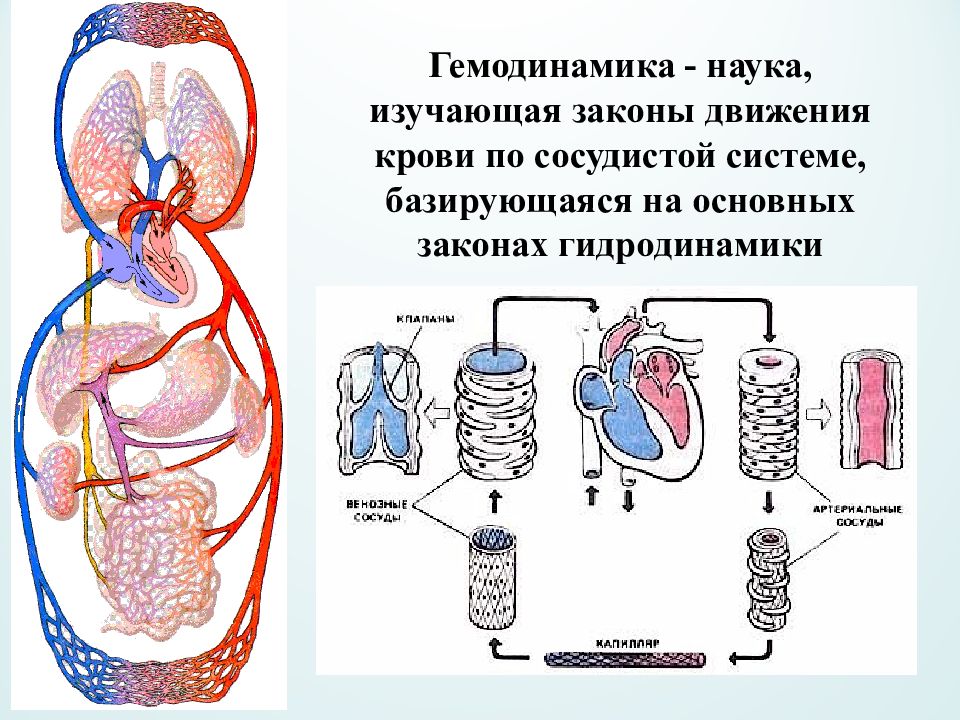
Гемодинамика - наука, изучающая законы движения крови по сосудистой системе, базирующаяся на основных законах гидродинамики
Слайд 10
Условие неразрывности струи в гемодинамике В любом сечении сердечно-сосудистой системы объемная скорость кровотока одинакова
Слайд 11
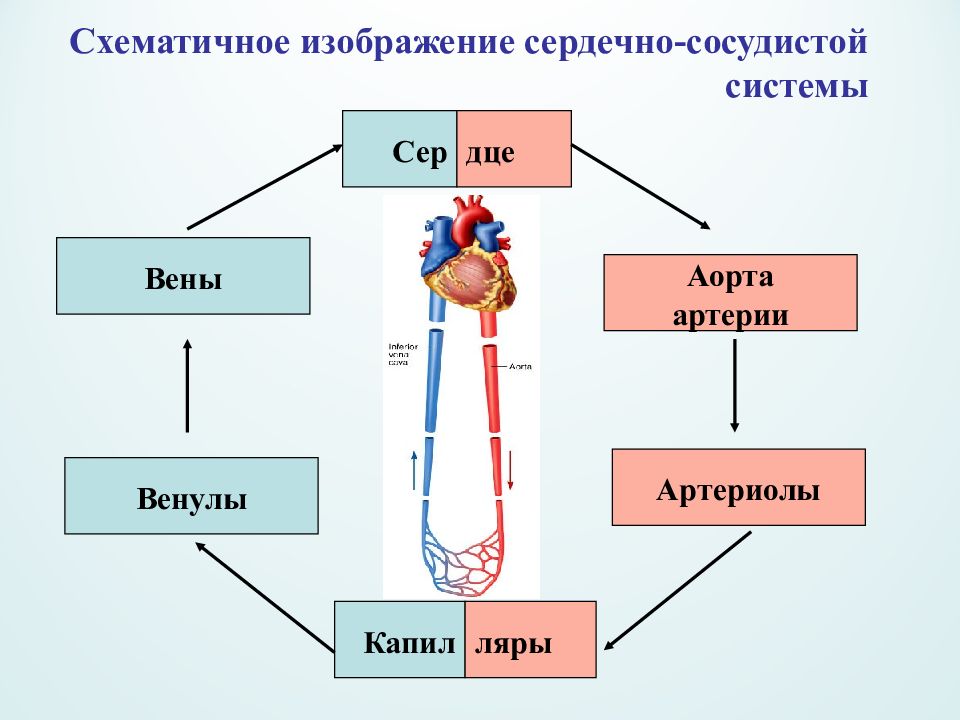
Схематичное изображение сердечно-сосудистой системы Аорта артерии Артериолы Вены Венулы Сер дце Капил ляры
Слайд 12
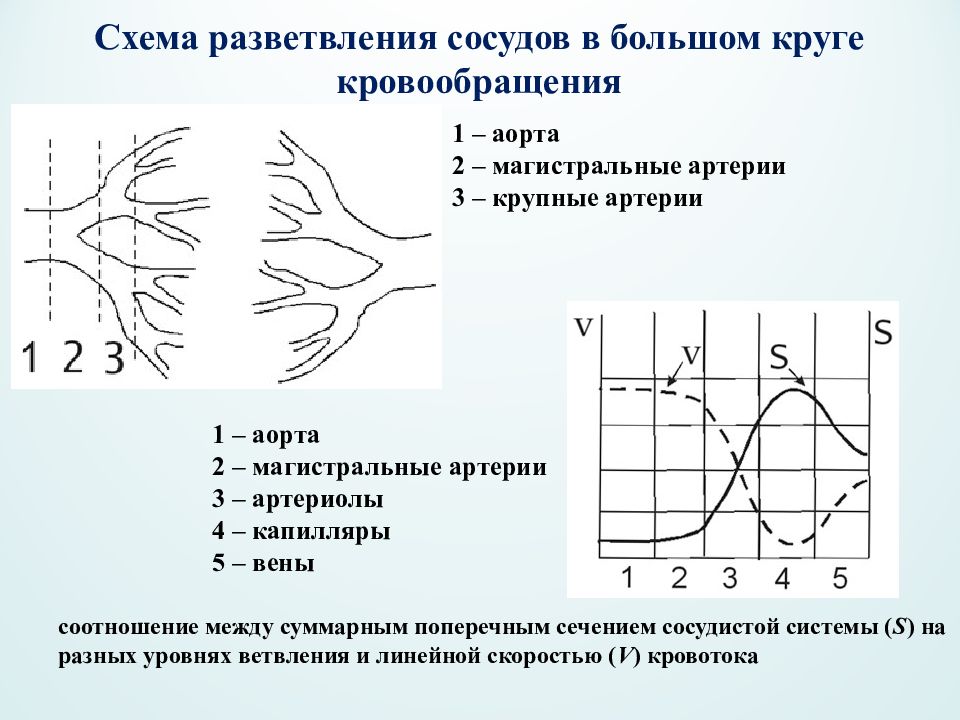
Схема разветвления сосудов в большом круге кровообращения 1 – аорта 2 – магистральные артерии 3 – крупные артерии соотношение между суммарным поперечным сечением сосудистой системы ( S ) на разных уровнях ветвления и линейной скоростью ( V ) кровотока 1 – аорта 2 – магистральные артерии 3 – артериолы 4 – капилляры 5 – вены
Слайд 14
Уравнение Бернулли описывает течение идеальной жидкости, т.е. абсолютно несжимаемой и невязкой жидкости т рубк а тока идеальной жидкости с дв умя выдел енными сечения ми площадью S 1 и S 2 1700-1782
Слайд 15
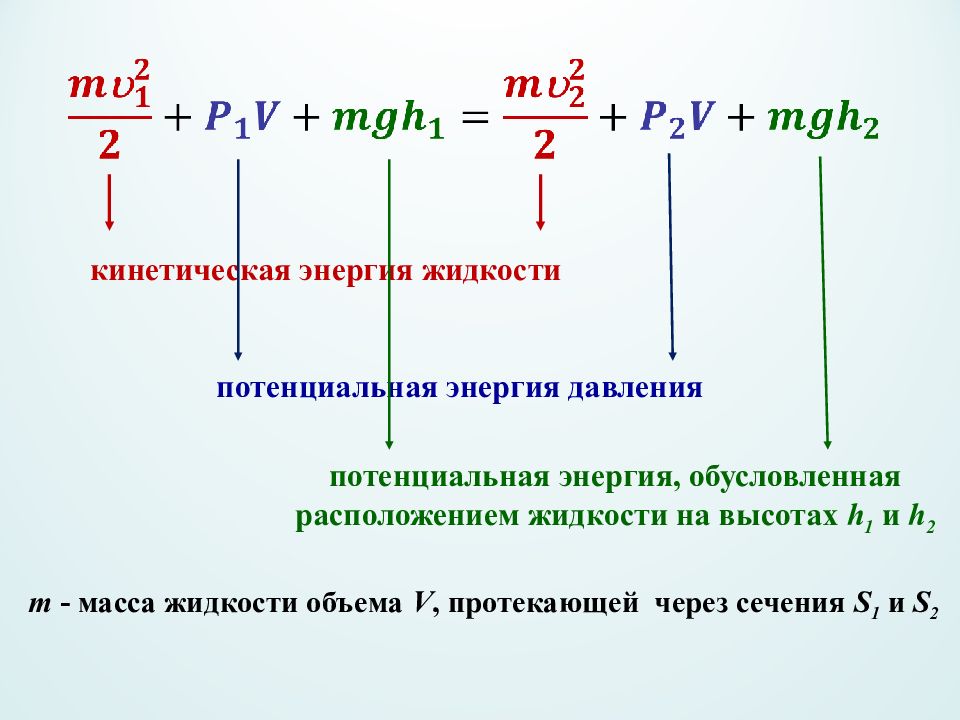
m - масса жидкости объема V, протекающей через сечения S 1 и S 2 кинетическая энергия жидкости потенциальная энергия давления потенциальная энергия, обусловленная расположением жидкости на высотах h 1 и h 2
Слайд 16
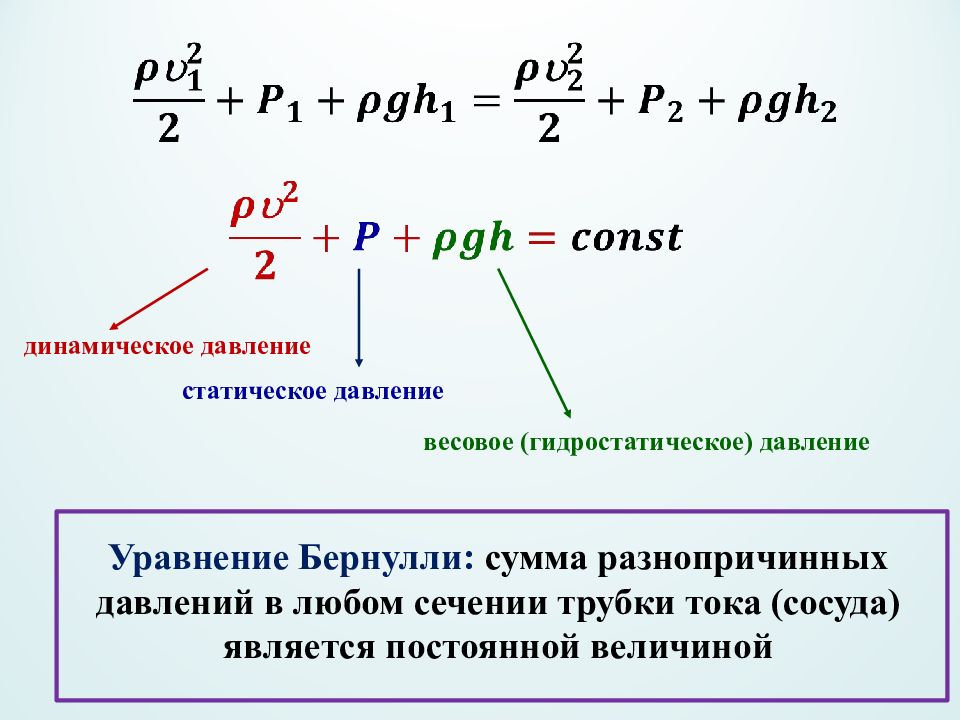
Уравнение Бернулли: сумма разнопричинных давлений в любом сечении трубки тока (сосуда) является постоянной величиной динамическое давление статическое давление весовое (гидростатическое) давление
Слайд 17
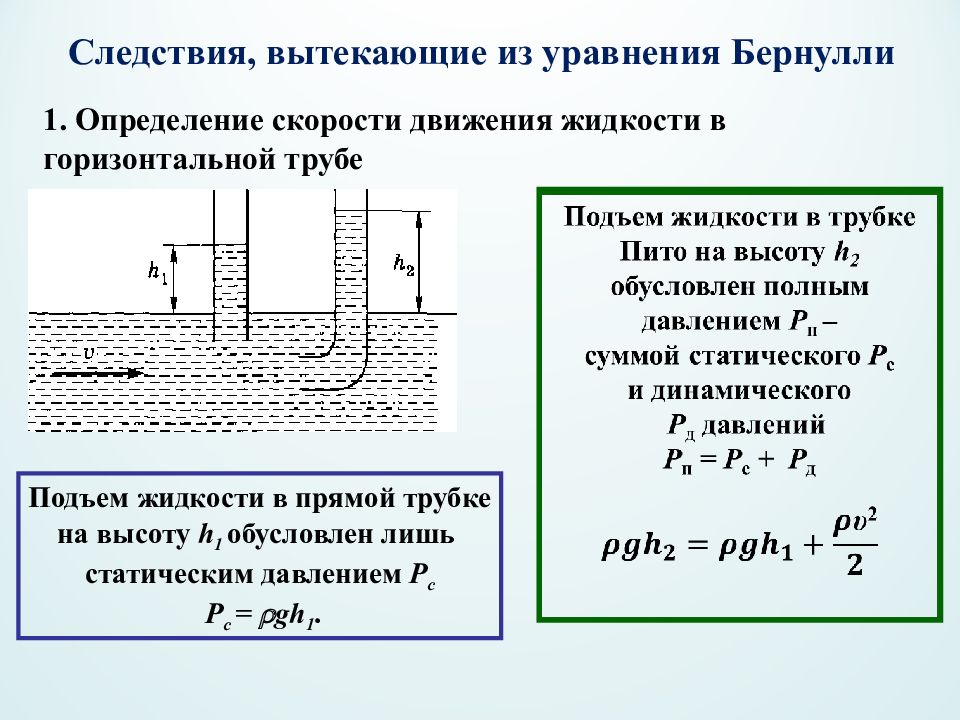
Подъем жидкости в прямой трубке на высоту h 1 обусловлен лишь статическим давлением Р c P c = gh 1. Следствия, вытекающие из уравнения Бернулли 1. Определение скорости движения жидкости в горизонтальной трубе
Слайд 18
Из последнего уравнения находим скорость течения жидкости Измеряя разность уровней жидкости в прямой и изогнутой трубках, можно определить скорость течения жидкости
Слайд 19
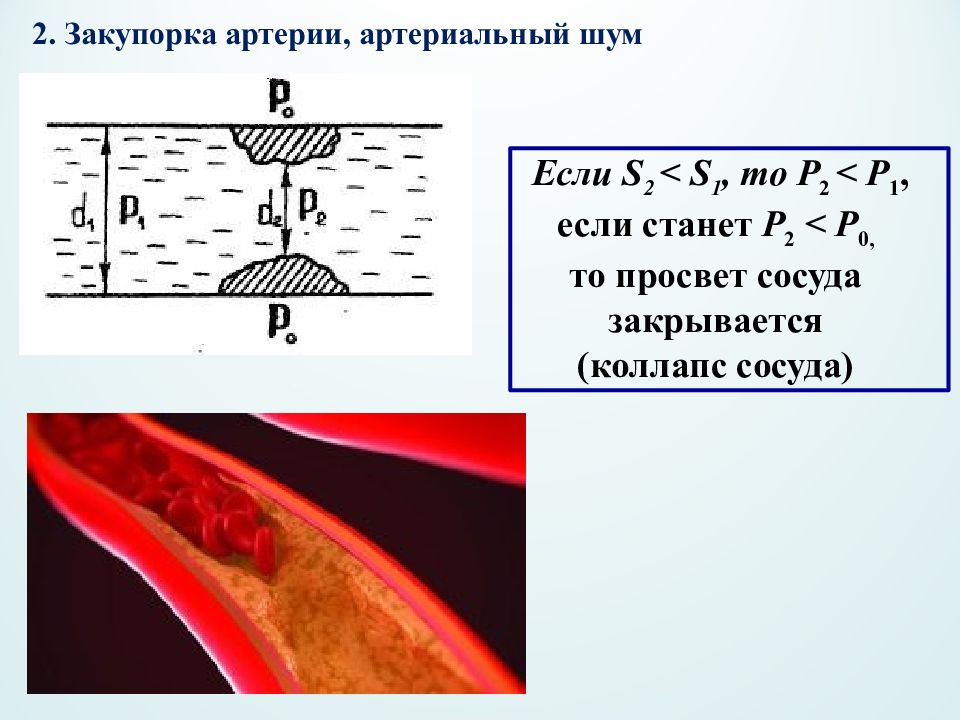
2. Закупорка артерии, артериальный шум Если S 2 < S 1, то Р 2 < Р 1, если станет Р 2 < Р 0, то просвет сосуда закрывается (коллапс сосуда)
Слайд 20
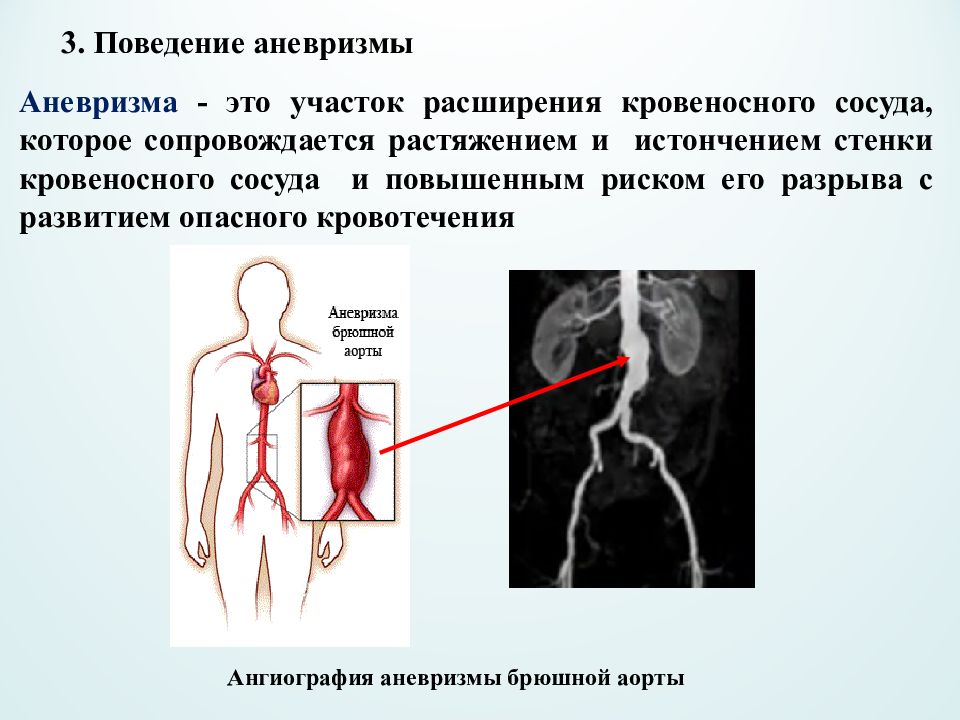
3. Поведение аневризмы Аневризма - это участок расширения кровеносного сосуда, которое сопровождается растяжением и истончением стенки кровеносного сосуда и повышенным риском его разрыва с развитием опасного кровотечения Ангиография аневризмы брюшной аорты
Слайд 21
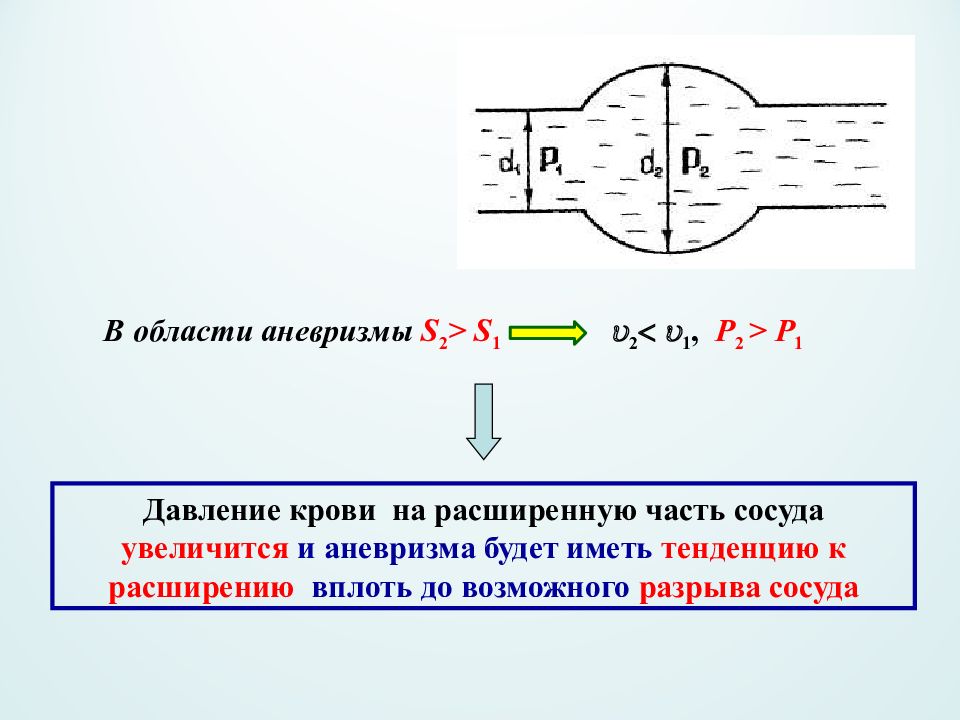
В области аневризмы S 2 > S 1 2 1, Р 2 > Р 1 Давление крови на расширенную часть сосуда увеличится и аневризма будет иметь тенденцию к расширению вплоть до возможного разрыва сосуда
Слайд 22
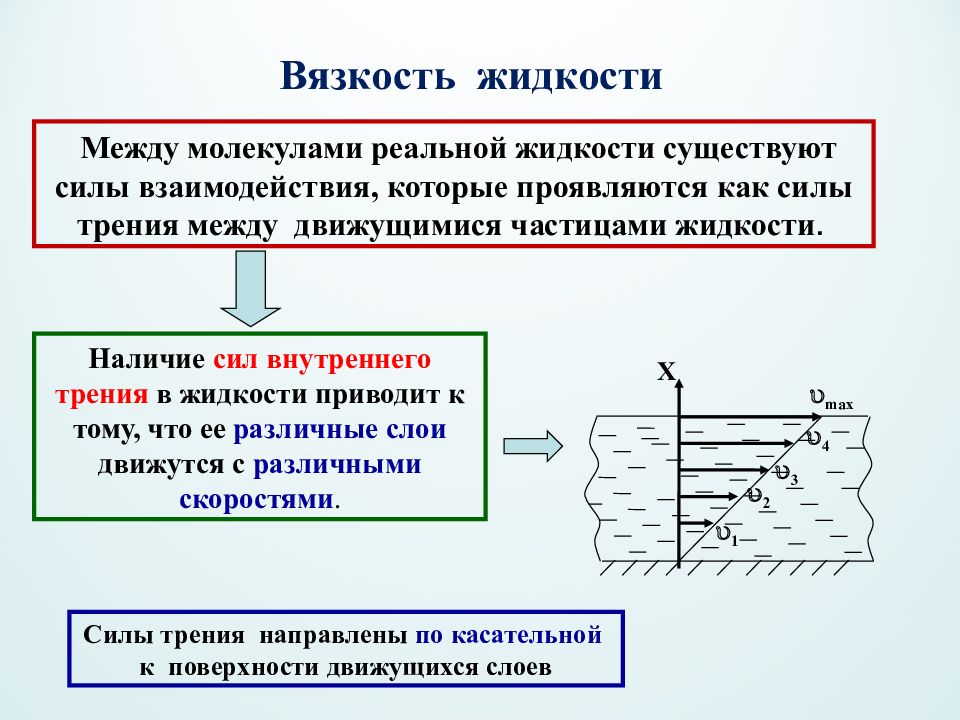
Вязкость жидкости Между молекулами реальной жидкости существуют силы взаимодействия, которые проявляются как силы трения между движущимися частицами жидкости. Наличие сил внутреннего трения в жидкости приводит к тому, что ее различные слои движутся с различными скоростями. 2 1 3 4 max Х Силы трения направлены по касательной к поверхности движущихся слоев
Слайд 24
СИ Внесистемные единицы Па. с 1мПа. с = 0,001 Па·с пуаз (П) сантипуаз 1 сП = 0,01 П Вязкост ь жидкости всегда зависит от: природы жидкости; температуры жидкости ( с увеличением температуры вязкость , как правило, уменьшается). Единицы измерения вязкости : 1 Па·с = 10 П ; 1 мПа·с = 1 сП Вязкость воды при 20 о С равна 1 мПа·с = 1 сП
Слайд 25
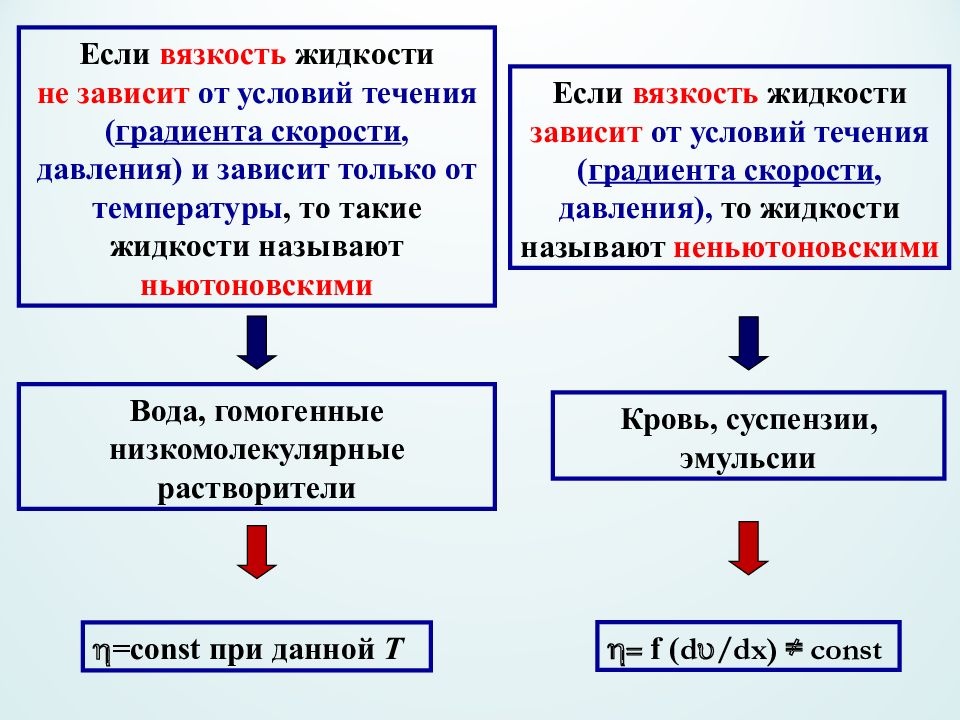
= const при данной T Вода, гомогенные низкомолекулярные растворители Если вязкость жидкости не зависит от условий течения ( градиента скорости, давления) и зависит только от температуры, то такие жидкости называют ньютоновскими = f ( d /dx ) ≠ const Кровь, суспензии, эмульсии Если вязкость жидкости зависит от условий течения ( градиента скорости, давления), то жидкости называют неньютоновскими
Слайд 26
Течение вязкой жидкости. Формула Пуазейля Объем V вязкой жидкости, ламинарно протекающей по участку гладкой трубы длиной L и радиусом r за время t, определяется формулой Пуазейля V t (времен z истечения жидкости) ; V ( Р 1 – Р 2 ) (перепаду давлений) ; V r 4 S 2 ; !!! V 1 / ( вязкости); V 1 / L 2 r P 2 P 1 L
Слайд 27
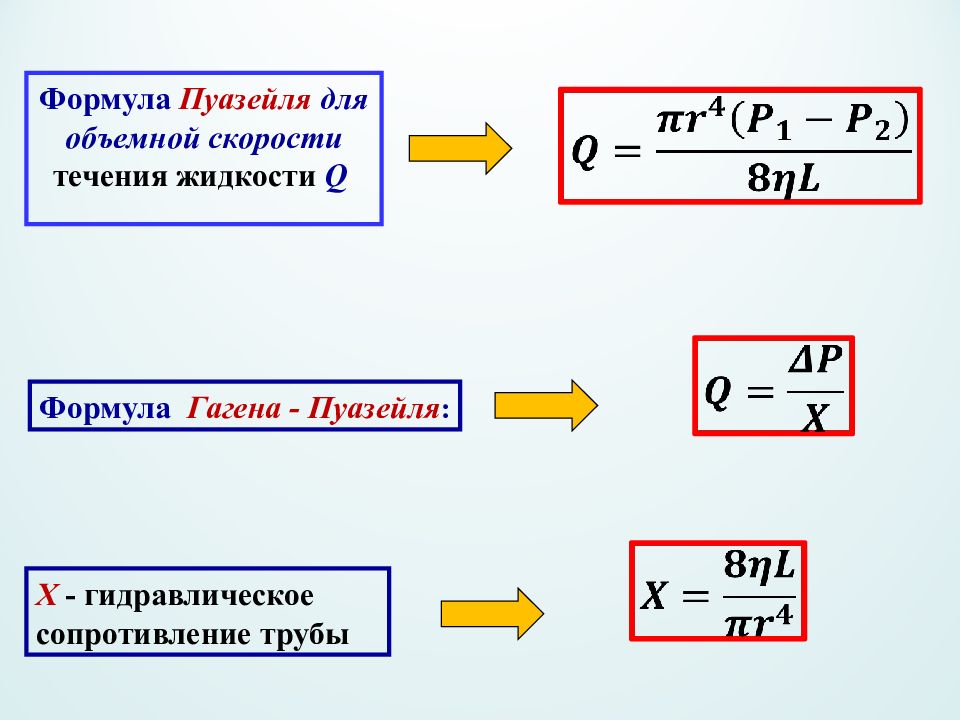
Формула Пуазейля для объемной скорости течения жидкости Q X - гидравлическое сопротивление трубы Формула Гагена - Пуазейля :
Слайд 28
- плотность жидкости; - средняя скорость течения жидкости; d – диаметр трубы; - вязкость жидкости Характер течения жидкости – ламинарный или турбулентный – определяетс я безразмерным числом Рейнольдса 1842–1912
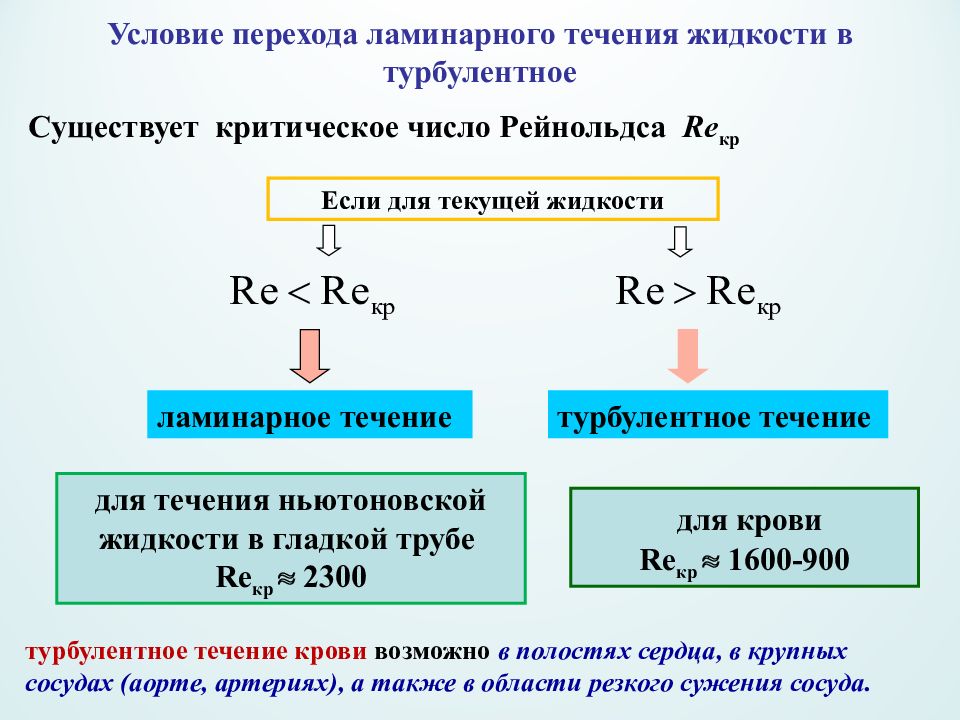
турбулентное течение крови возможно в полостях сердца, в крупных сосудах (аорте, артериях), а также в области резкого сужения сосуда. Существует критическое число Рейнольдса Re кр Если для текущей жидкости турбулентное течение ламинарное течение для течения ньютоновской жидкости в гладкой трубе Re кр 2300 для крови Re кр 1600-900
Слайд 30
Методы определения вязкости жидкости Метод Стокса (метод падающего шарика) Капиллярный метод (вискозиметр Оствальда) Ротационный метод (вискозиметр Куэтта)
Слайд 31
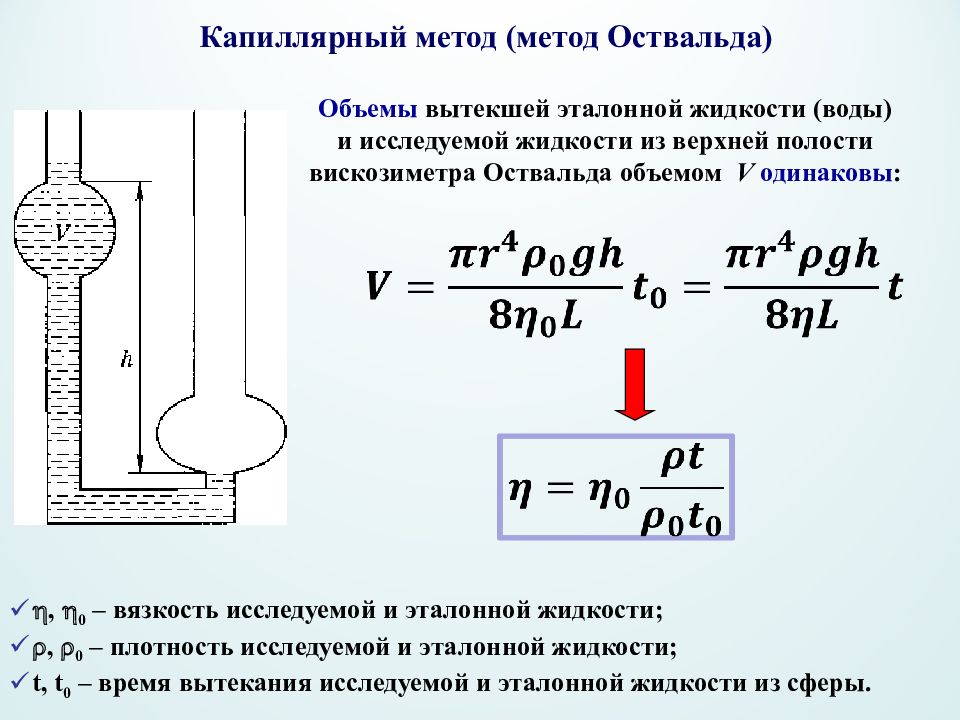
Капиллярный метод (метод Оствальда ) Объемы вытекшей эталонной жидкости (воды) и исследуемой жидкости из верхней полости вискозиметра Оствальда объемом V одинаковы : , 0 – вязкость исследуемой и эталонной жидкости; , 0 – плотность исследуемой и эталонной жидкости; t, t 0 – время вытекания исследуемой и эталонной жидкости из сферы.
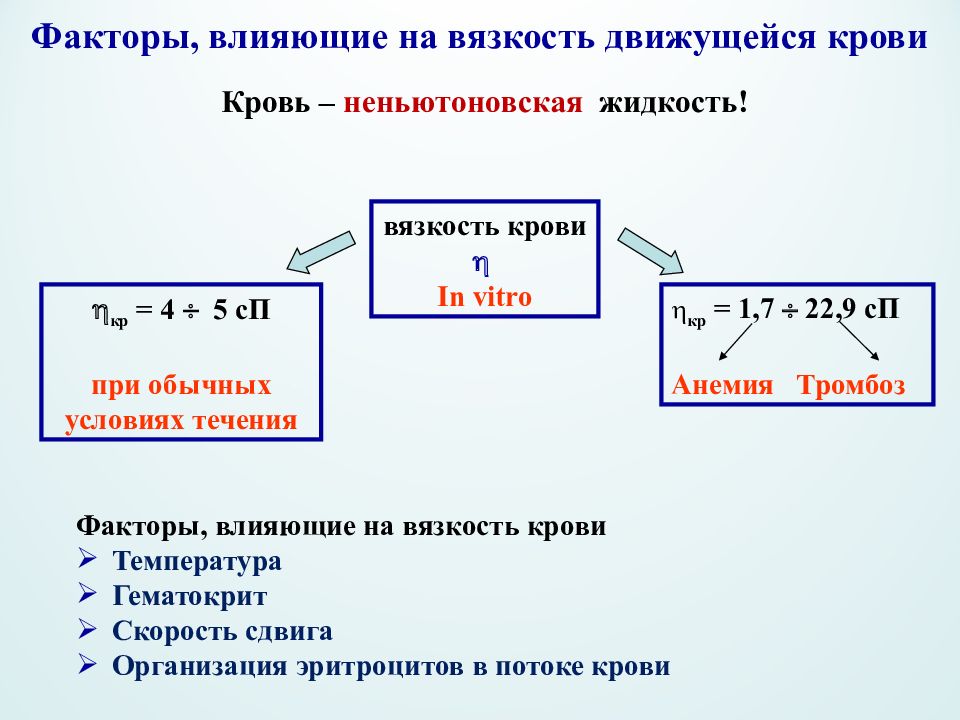
Факторы, влияющие на вязкость крови Температура Гематокрит Скорость сдвига Организация эритроцитов в потоке крови кр = 4 5 сП при обычных условиях течения вязкость крови In vitro кр = 1,7 22,9 сП Анемия Тромбоз Кровь – неньютоновская жидкость!
Слайд 33
Влияние температуры на вязкость крови Для ньютоновских жидкостей с ростом температуры вязкость уменьшается. Изменение температуры может приводить к изменению степени агрегации как эритроцитов, так и тромбоцитов и вызывать другие изменения в структуре крови. Влияние температурного фактора на вязкость крови неоднозначно.
Слайд 34
Гематокрит Гематокрит - (Ht или HCT) отношение суммарного объема эритроцитов ( V эр) к объему крови ( V кр), в котором они содержатся : Ht = Vэр / Vкр В норме для мужчин Ht = Vэр/Vкр 0,42 – 0,54; для женщин Ht = Vэр/Vкр 0,38 – 0,46. С повышением гематокрита вязкость крови возрастает. Вязкость венозной крови больше, чем артериальной, т.к., из-за повышенного содержания углекислого газа, эритроциты в венозной крови имеют большие размеры ( объем) и другую форму (сферическую).
Слайд 35
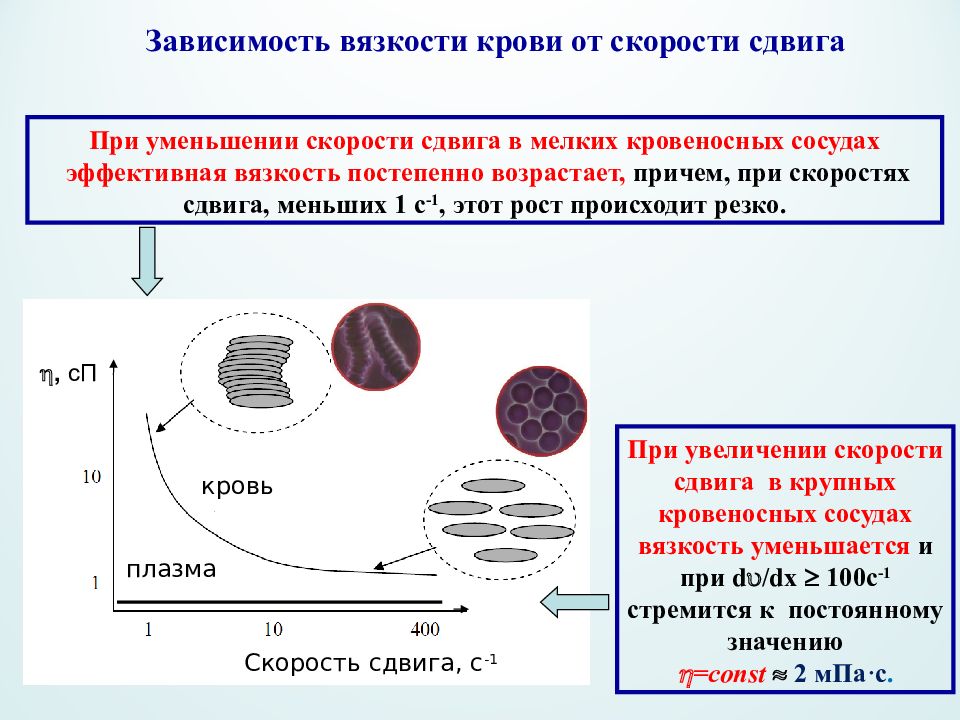
Скорость сдвига, с -1 , сП плазма кровь Зависимость вязкости крови от скорости сдвига При уменьшении скорости сдвига в мелких кровеносных сосудах эффективная вязкость постепенно возрастает, причем, при скоростях сдвига, меньших 1 с -1, этот рост происходит резко. При увеличении скорости сдвига в крупных кровеносных сосудах вязкость уменьшается и при d / dx 100c -1 стремится к постоянному значению = const 2 мПа·с.
Слайд 36
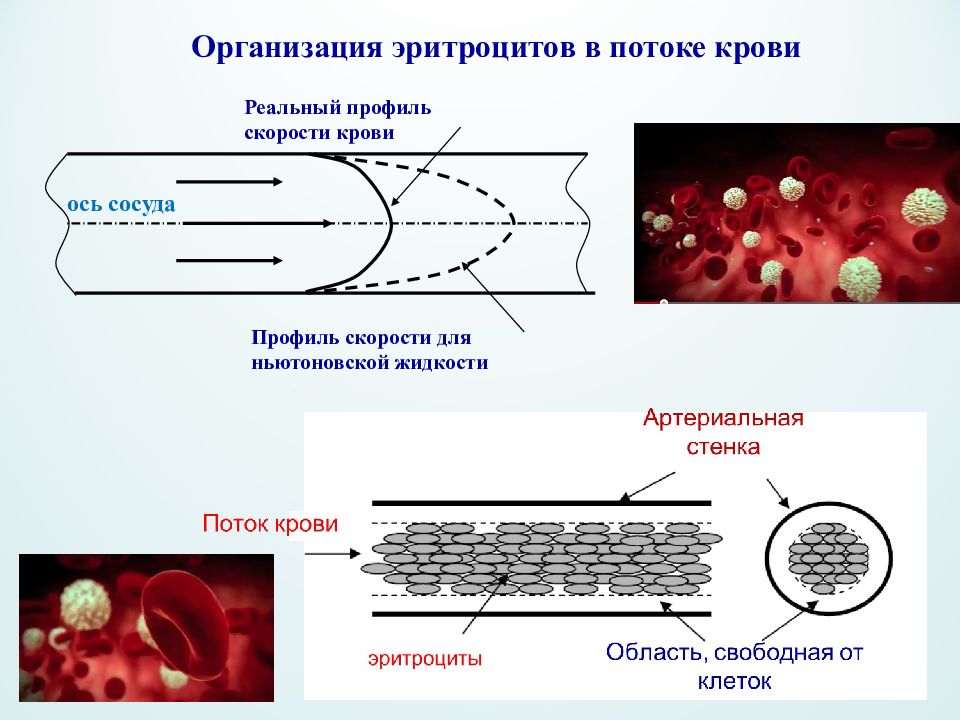
Организация эритроцитов в потоке крови ось сосуда Профиль скорости для ньютоновской жидкости Реальный профиль скорости крови
Слайд 37
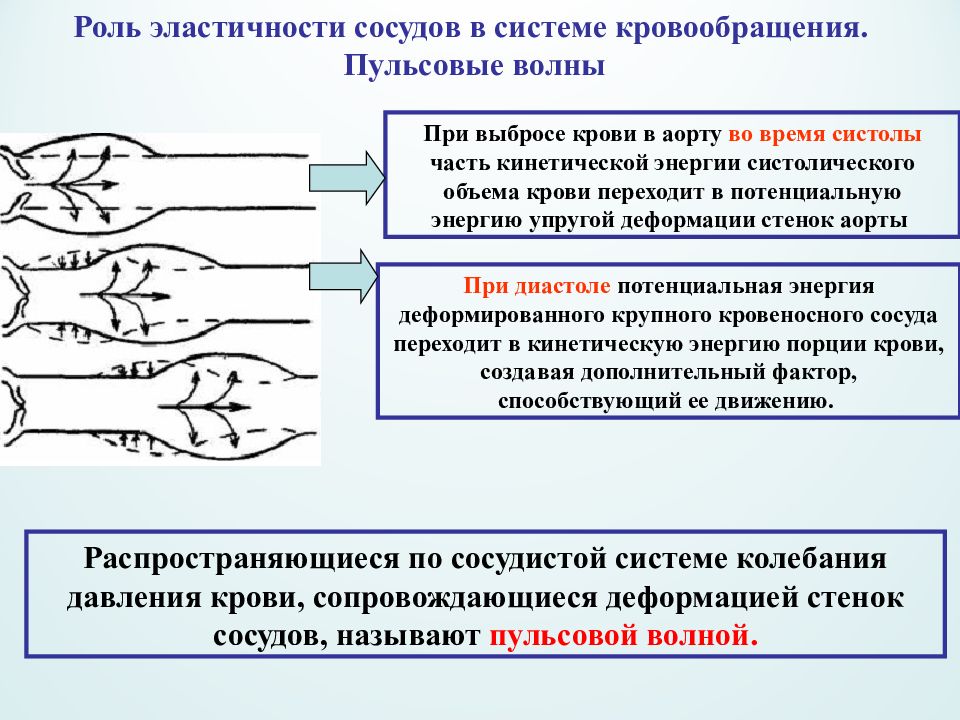
Роль эластичности сосудов в системе кровообращения. Пульсовые волны При выбросе крови в аорту во время систолы часть кинетической энергии систолического объема крови переходит в потенциальную энергию упругой деформации стенок аорты При диастоле потенциальная энергия деформированного крупного кровеносного сосуда переходит в кинетическую энергию порции крови, создавая дополнительный фактор, способствующий ее движению. Распространяющиеся по сосудистой системе колебания давления крови, сопровождающиеся деформацией стенок сосудов, называют пульсовой волной.
Слайд 38
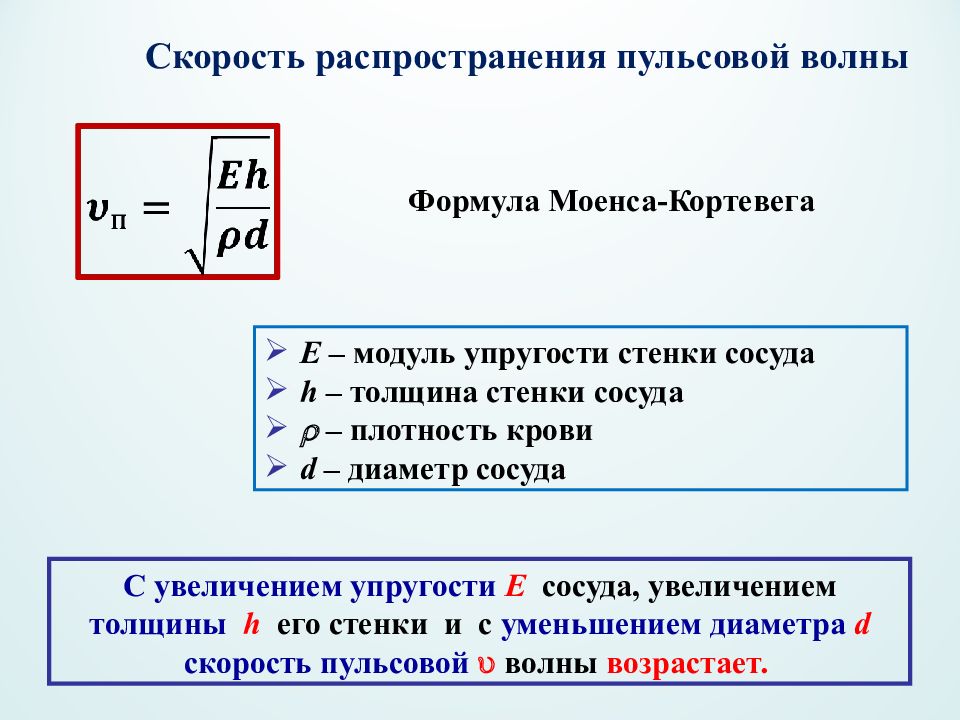
Скорость распространения пульсовой волны Формула Моенса-Кортевега Е – модуль упругости стенки сосуда h – толщина стенки сосуда – плотность крови d – диаметр сосуда С увеличением упругости Е сосуда, увеличением толщины h его стенки и c уменьшением диаметра d скорость пульсовой волны возрастает.
Слайд 39
В аорте скорость пульсовой волны п = 4 – 6 м/с. В артериях п = 8 –12 м/с, т.к. они имеют малый диаметр и толстый мышечный слой. В полой вене, обладающей большей эластичностью, п ≈ 1 м/с ДЛЯ СРАВНЕНИЯ: Линейная скорость кровотока в аорте кр ≈ 0,5 м/с (в покое)
Слайд 40
в любой точке сосудистой системы давление крови Распределение давления в сосудистой системе p 0 – атмосферное давление (давление в правом предсердии); gh - гидростатическое давление, обусловленное весом кровяного столба высотой h и плотностью ; p С – давление, создаваемое работой сердца.
Слайд 41
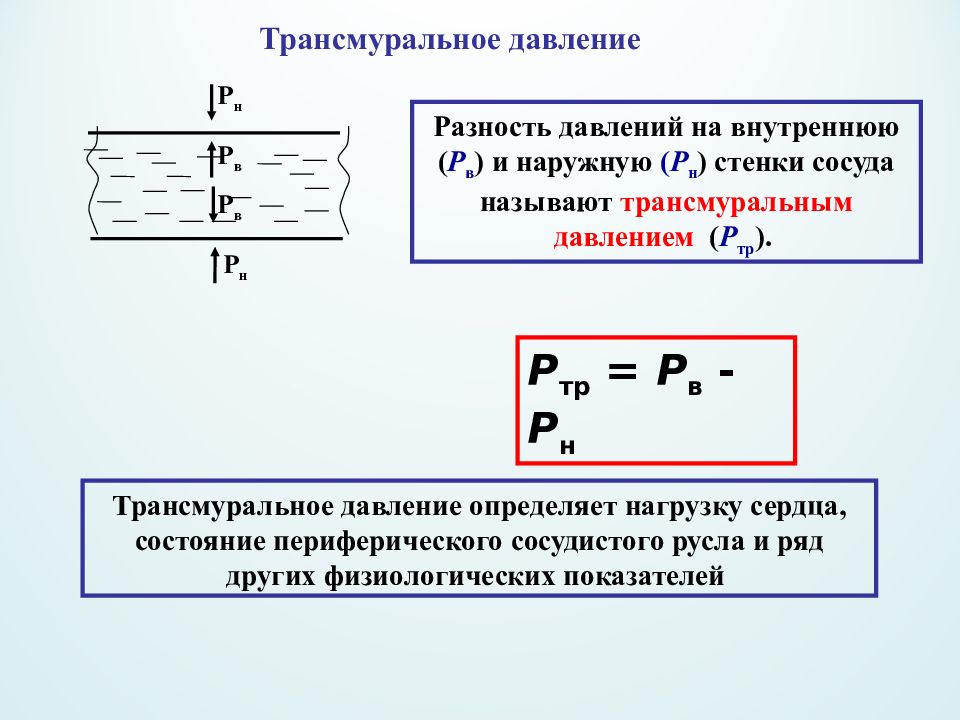
Трансмуральное давление Разность давлений на внутреннюю ( Р в ) и наружную ( Р н ) стенки сосуда называют трансмуральным давлением ( Р т p ). Р в Р в Р н Р н Р т p = Р в - Р н Трансмуральное давление определяет нагрузку сердца, состояние периферического сосудистого русла и ряд других физиологических показателей
Слайд 42
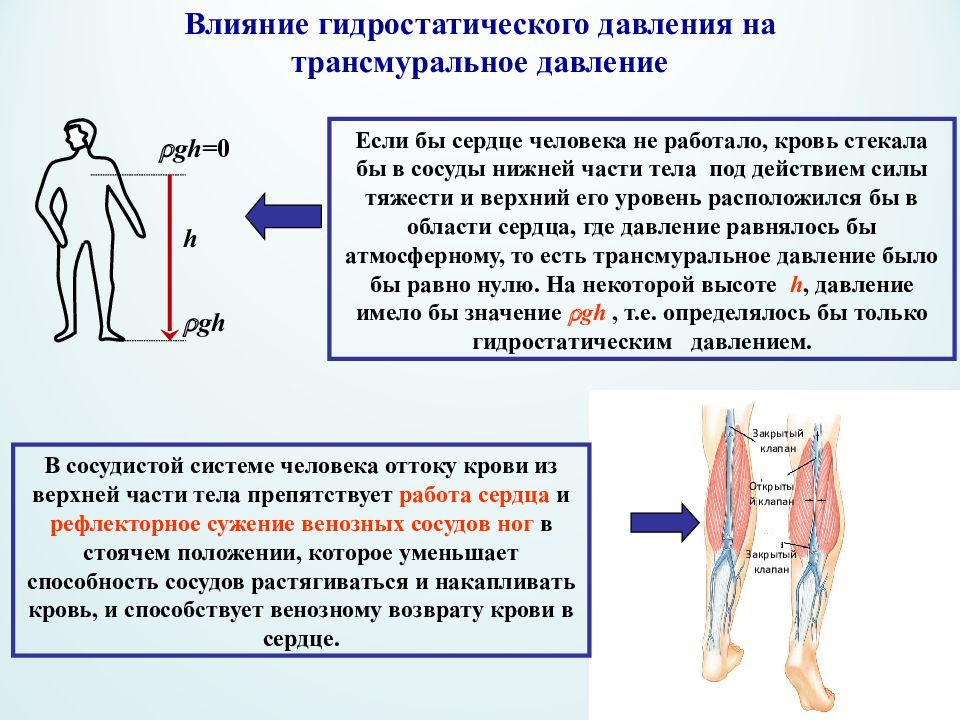
Закрытый клапан Закрытый клапан Открытый клапан Влияние гидростатического давления на т рансмуральное давление Если бы сердце человека не работало, кровь стекала бы в сосуды нижней части тела под действием силы тяжести и верхний его уровень расположился бы в области сердца, где давление равнялось бы атмосферному, то есть трансмуральное давление было бы равно нулю. На некоторой высоте h, давление имело бы значение gh, т.е. определялось бы только гидростатическим давлением. В сосудистой системе человека оттоку крови из верхней части тела препятствует работа сердца и рефлекторное сужение венозных сосудов ног в стоячем положении, которое уменьшает способность сосудов растягиваться и накапливать кровь, и способствует венозному возврату крови в сердце. gh gh =0 h
Слайд 43
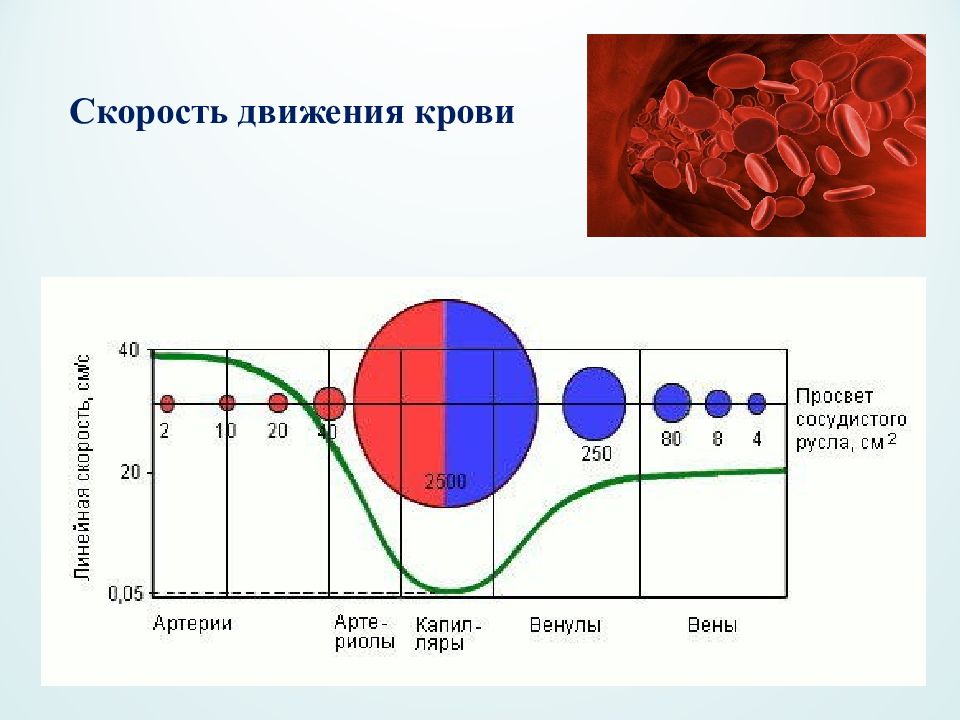
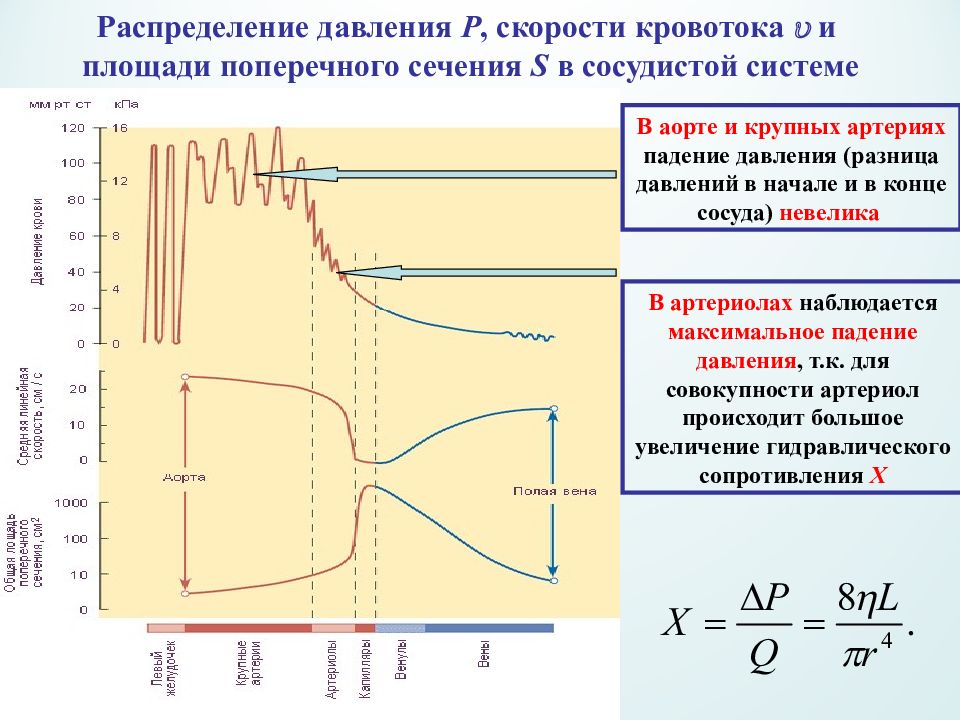
В аорте и крупных артериях падение давления (разница давлений в начале и в конце сосуда) невелика В артериолах наблюдается максимальное падение давления, т.к. для совокупности артериол происходит большое увеличение гидравлического сопротивления Х Распределение давления Р, скорости кровотока и площади поперечного сечения S в сосудистой системе
Слайд 44
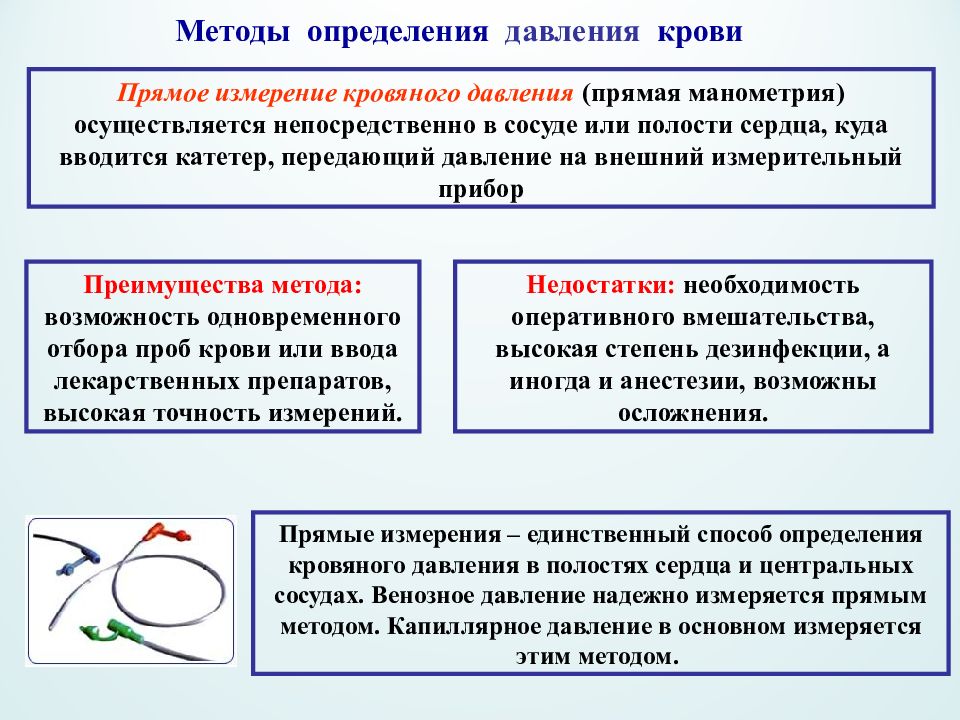
Прямое измерение кровяного давления (прямая манометрия) осуществляется непосредственно в сосуде или полости сердца, куда вводится катетер, передающий давление на внешний измерительный прибор Преимущества метода: возможность одновременного отбора проб крови или ввода лекарственных препаратов, высокая точность измерений. Недостатки: необходимость оперативного вмешательства, высокая степень дезинфекции, а иногда и анестезии, возможны осложнения. Прямые измерения – единственный способ определения кровяного давления в полостях сердца и центральных сосудах. Венозное давление надежно измеряется прямым методом. Капиллярное давление в основном измеряется этим методом. Методы определения давления крови
Слайд 45
Непрямые измерения кровяного давления (компрессионные) осуществляются без нарушения целостности сосудов и тканей путем уравновешивания давления внутри сосуда известным внешним давлением через его стенку и мягкие ткани тела. П альпаторный метод Рива- Роччи Измер яется систолическое давлени е посредством прощупывания пульса на лучевой артерии после создания высокого давления в манжете, наложенной на плечо, и последующей медленной декомпрессии. Основан на установлении систолического и диастолического давления по возникновению и исчезновению в артерии особых звуковых явлений - тонов Короткова. Аускультативный метод
Слайд 46
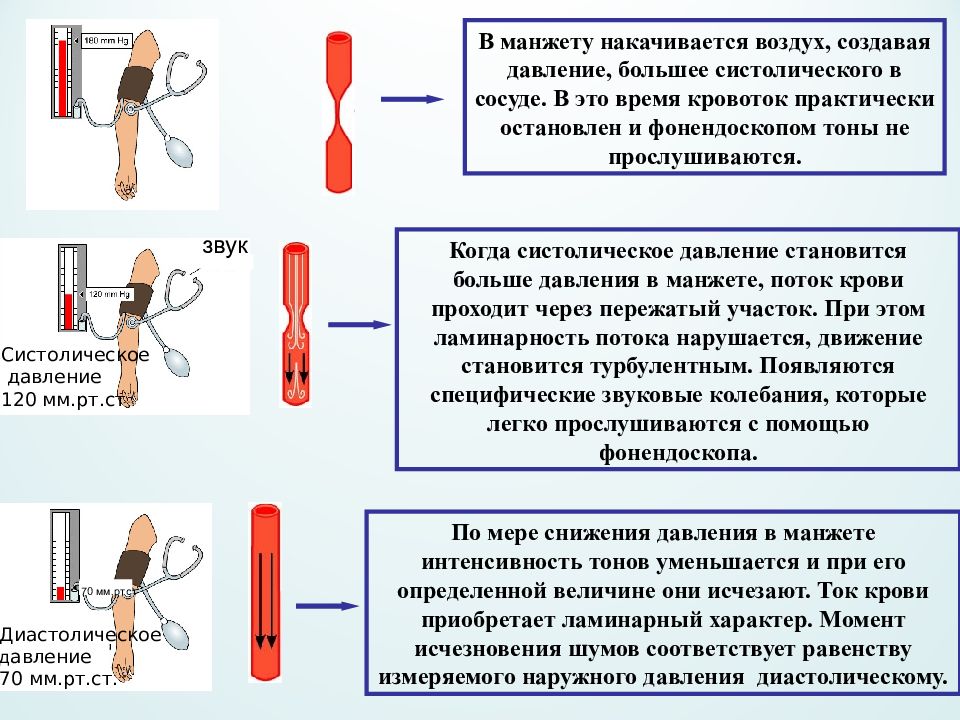
В манжету накачивается воздух, создавая давление, большее систолического в сосуде. В это время кровоток практически остановлен и фонендоскопом тоны не прослушиваются. Когда систолическое давление становится больше давления в манжете, поток крови проходит через пережатый участок. При этом ламинарность потока нарушается, движение становится турбулентным. Появляются специфические звуковые колебания, которые легко прослушиваются с помощью фонендоскопа. По мере снижения давления в манжете интенсивность тонов уменьшается и при его определенной величине они исчезают. Ток крови приобретает ламинарный характер. Момент исчезновения шумов соответствует равенству измеряемого наружного давления диастолическому. звук Систолическое давление 120 мм.рт.ст Диастолическое д авление 70 мм.рт.ст. 70 мм.рт.ст
Слайд 47
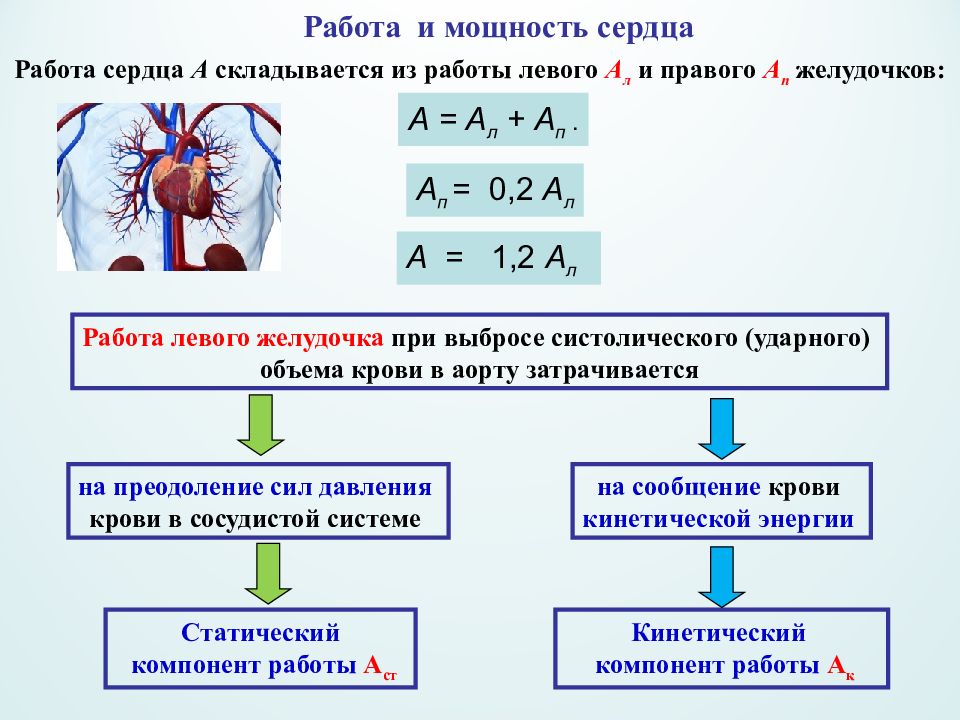
Работа и мощность сердца А = А л + А п. Работа сердца А складывается из работы левого А л и правого А п желудочков: А п = 0,2 А л А = 1,2 А л Работа левого желудочка при выбросе систолического (ударного) объема крови в аорту затрачивается на преодоление сил давления крови в сосудистой системе на сообщение крови кинетической энергии Статический компонент работы А ст Кинетический компонент работы А к
Слайд 48
Статический компонент работы сердца А ст P c р - среднее давление крови в аорте: P ср = 100 мм.рт.ст.=13,3 кПа V с - систолический объем крови в покое: V c 60 мл = 6. 10 -5 м 3 А ст ≈ 0,8 Дж
Слайд 49
Кинетический компонент работы сердца А к ρ – плотность крови (ρ ≈ 1,05. 10 3 кг/м 3 ); – линейная скорость крови в аорте ( ≈ 0,5 м/с); V c – систолический объем крови в покое ( V c 60 мл = 6. 10 -5 м 3 ). А к ≈ 0,008 Дж
Слайд 50
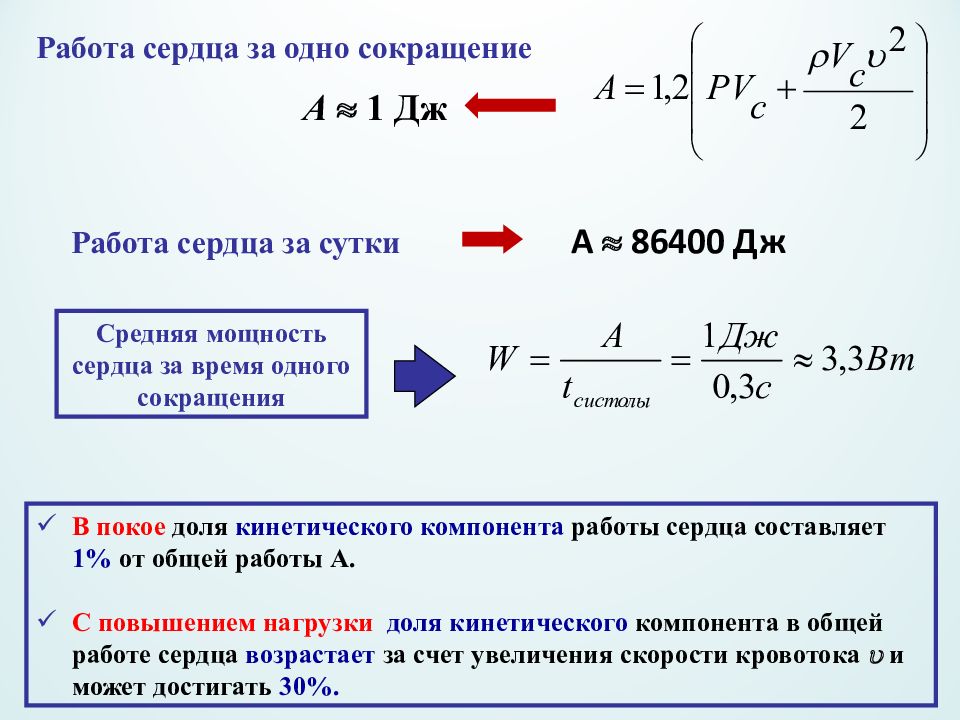
Работа сердца за одно сокращение А 1 Дж Работа сердца за сутки А 86400 Дж Средняя мощность сердца за время одного сокращения В покое доля кинетического компонента работы сердца составляет 1% от общей работы А. С повышением нагрузки доля кинетического компонента в общей работе сердца возрастает за счет увеличения скорости кровотока и может достигать 30%.