Первый слайд презентации: ЛЕКЦИЯ № 5 (ф) Тема: Биомеханика. Процессы переноса в биологических системах (часть 1 )
Слайд 2: План лекции:
Внутреннее трение (вязкость). Уравнение Ньютона Ламинарное и турбулентное тече-ния. Число Рейнольдса. Формула Пуазейля.Уравнение Бернулли 3. Методы определения вязкости крови
Слайд 3: БИОМЕХАНИКА -
раздел биофизики, в котором рассматриваются механические свойства живых тканей и органов, а также механические явления, происходящие как с целым организмом, так и с отдельными его органами.
Слайд 4: ГЕМОДИНАМИКА -
область биомеханики, в которой исследуется движение крови по сосудистой системе. Физической основой гемодинамики является гидродинамика.
Слайд 5: Необходимо помнить следующее:
а) при изучении жидкостей в покое нет необходимости различать реальные и идеальные жидкости. Их свойства однотипны; б) при изучении движущихся жидкостей необходимо дополнительно учитывать силы трения, возникающие в реальных жидкостях, т.е. их вязкость.
Слайд 6: ВЯЗКОСТЬ (внутреннее трение) -
- явление при течении реальной жидкости, когда отдельные слои ее воздействуют друг на друга с силами, касательными к слоям.
Слайд 8: УРАВНЕНИЕ НЬЮТОНА -
F тр = η • • S, где d υ /dx - градиент скорости (скорость сдвига) η - коэффициент пропорциональ-ности, называемый коэффициентом внутреннего трения, или вязкостью S - площадь соприкосновения слоев
Слайд 9: ЕДИНИЦА ВЯЗКОСТИ:
СИ: 1 паскаль-секунда (Па • с). СГС : 1пуаз (П) 1 Па • с = 10 П.
Слайд 10: НЬЮТОНОВСКИЕ ЖИДКОСТИ:
жидкости, вязкость которых не за-висит от градиента скорости (вяз-кость постоянна). Такие жидкости подчиняются урав-нению Ньютона ( вода, глицерин, воздух, ртуть и т.д.)
Слайд 11: НЕНЬЮТОНОВСКИЕ ЖИДКОСТИ:
жидкости, вязкость которых зави-сит от градиента скорости (вязкость не постоянная). Такие жидкости не подчиняются уравнению Ньютона (эмульсии, суспензии, пены) Кровь-неньютоновская жидкость,ее вязкость 0.004 Па •с (4 мПа•с)
Слайд 12: КРОВЬ:
в сосудах диаметром более 100 мкм и при скорости сдвига выше 100 1/с кровь ведет себя как ньютоновская жидкость в сосудах диаметром менее 100 мкм и при скорости сдвига ниже 100 1/с кровь ведет себя как неньютонов-ская жидкость
Слайд 13: ЭРИТРОЦИТЫ:
способность их к деформации при низких скоростях сдвига обра-зуют агрегаты в виде монетных столбиков при патологических процессах увеличивается жесткость их стенок
Слайд 18: УРАВНЕНИЕ ПУАЗЕЙЛЯ:
Q =, где R – радиус трубы (сосуда) η - вязкость жидкости (крови) ( p 1 - p 2 ) – перепад давлений на концах трубы (сосуда) l - длина трубы (сосуда)
Слайд 20: АНАЛОГИЯ:
Закон Ома Формула Пуазейля I = U/R Q = π R4/8 η · ( p 1 - p 2 )/ l или Q = ( p 1 - p 2 )/ Х U p 1 - p 2 I Q R Х = 8 η 1/( π R 4)
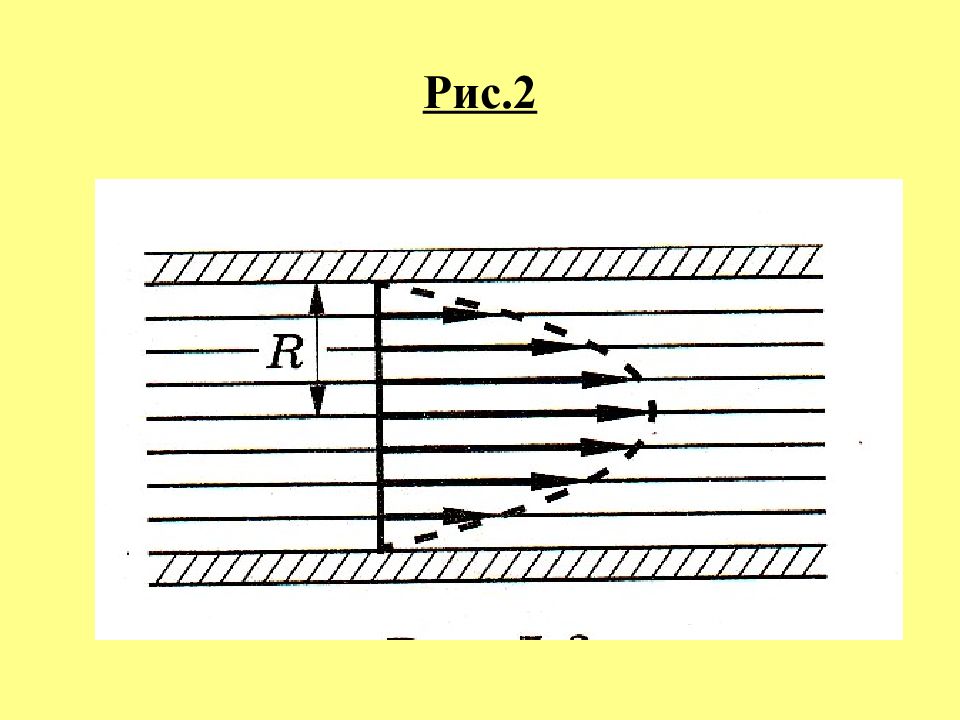
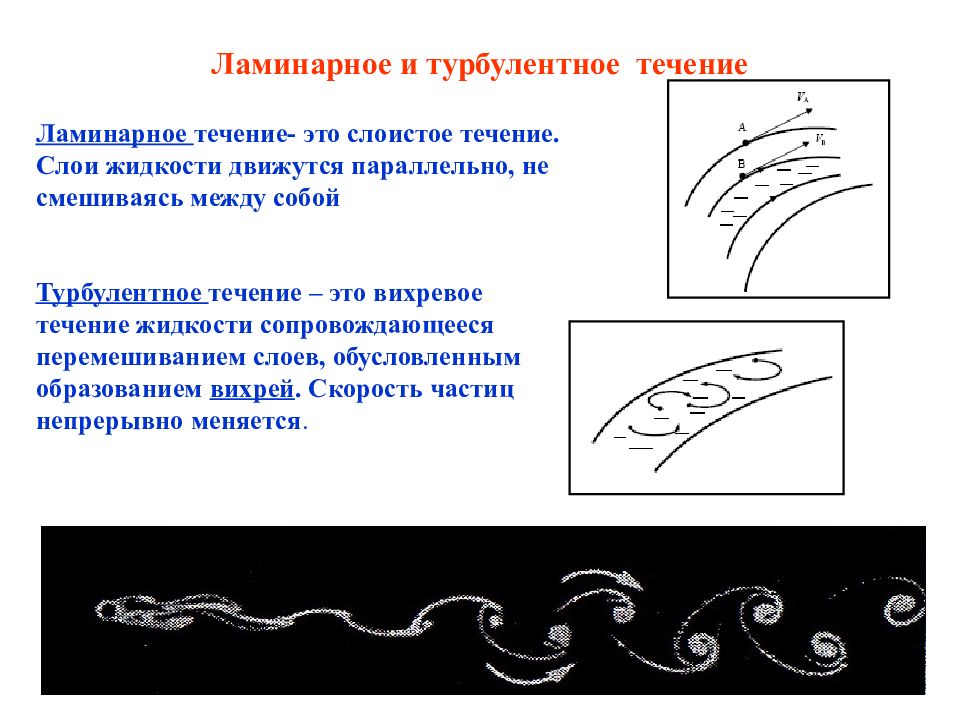
Слайд 22: Два характера течения жидкости:
ламинарное (слоистое, установив- шееся, стационарное) турбулентное ( вихревое, неустано-вившееся, нестационарное). Характер течения жидкости по тру-бе зависит от свойств жидкости, ско-рости ее течения, размеров трубы и определяется числом Рейнольдса
Слайд 23: ЧИСЛО РЕЙНОЛЬДСА:
, где ρ ж – плотность жидкости (крови) υ - скорость жидкости (крови) D – диаметр трубы (сосуда) η – вязкость жидкости (сосуда)
Слайд 24
Если число Рейнольдса больше некоторого критического ( R е > R е кр ), то движение жидкости турбулент-ное. Если число Рейнольдса меньше критического ( R е < R е кр ), то течение ламинарное.
Слайд 25: Физический смысл числа Рейнольдса:
а) когда Re <<1, мы можем сказать, что вязкие силы преобладают, а инерционные пренебрежимо малы. Например, на уровне микрососудов (сосуды диаметром порядка 100 мкм и менее) типичные числа Рейноль-дса меньше единицы и течение можно рассматривать как чисто вязкое;
Слайд 26
б) когда Re >>1, напротив, преоблада-ют инерционные силы, а вязкость (во всех областях, кроме погранич-ных) лишь незначительно изменяет характер течения. Например, для крови в крупных артериях, в венах.
Слайд 27: Средние числа Рейнольдса:
Аорта 1200 – 5800 Большие артерии 1000 – 100 Малые артерии, артериолы 10 – 0.01
Слайд 28
Капилляры 0.001 – 0.003 Венулы, малые вены 0.01 – 1 Большие вены 100 – 600 Полые вены 600 – 1000
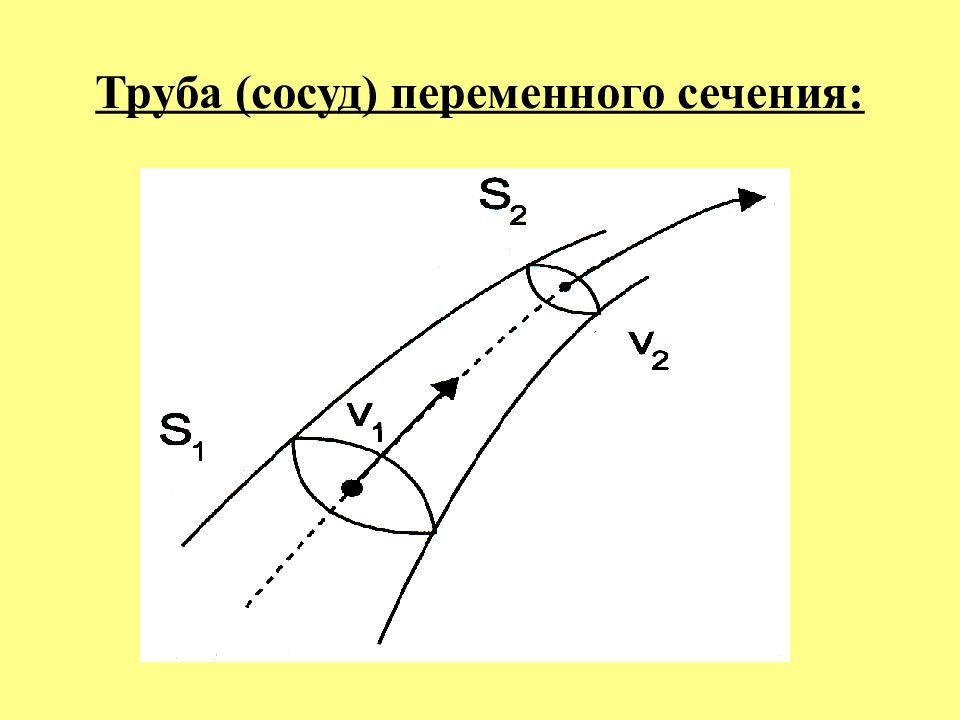
Слайд 30: УРАВНЕНИЕ НЕРАЗРЫВНОСТИ СТРУИ:
- масса жидкости, про-шедшая за время через некоторое сечение, равна масса жидкости, прошедшая через второе сечение за это же время,, где ρ1 и ρ2 - плотности жидкости в 1-м и во 2-м сечениях соответственно.
Слайд 31: УРАВНЕНИЕ НЕРАЗРЫВНОСТИ СТРУИ:
ρυ Ѕ = const, т.е. масса жидкости, протекающей ежесекундно через сечение Ѕ сохраняется Для несжимаемых жидкостей( ρ1 = ρ2 = ρ) : υ Ѕ = const или Q = const, т.к. Q = υ Ѕ, т.е. скорость движения жидкой струи обратно пропорци-ональна ее поперечному сечению.
Слайд 32: УРАВНЕНИЕ БЕРНУЛЛИ:
ρ gh + p + ρυ ²/2 = const, где ρ gh - гидростатическое давление (или удельная потенциальная энергия сил тяжести жидкости); p - статическое давление (или удельная потенциальная энергия сил давления); ρυ ²/2 - динамическое давление (или удельная кинетическая энергия).
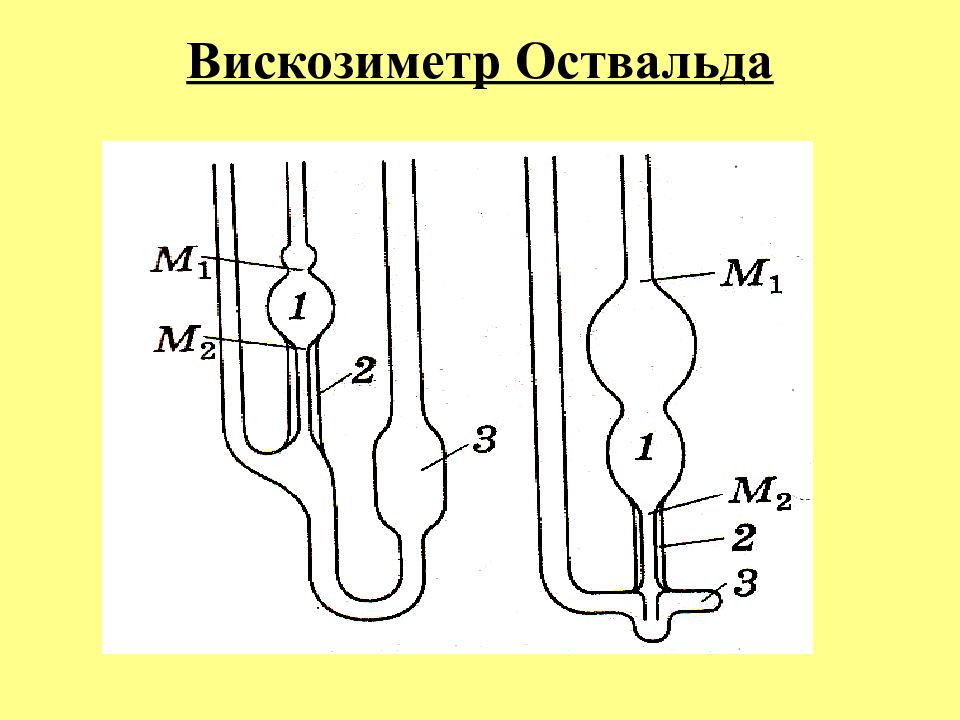
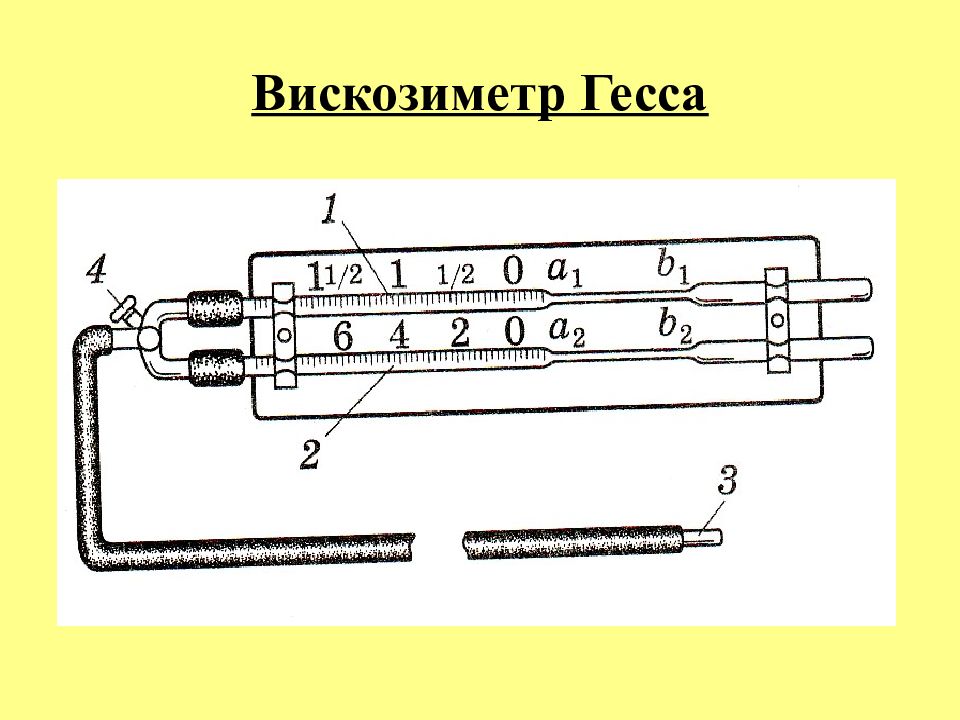
Слайд 33: МЕТОДЫ ИЗМЕРЕНИЯ ВЯЗКОСТИ:
1. Капиллярный метод основан на формуле Пуазейля и заключается в измерении времени протекания че-рез капилляр жидкости известной массы под действием силы тяжести при определенном перепаде давлений.
Слайд 37
2.Метод падающего шарика используется в вискозиметрах, основанных на законе Стокса. Измеряя скорость равномерного падения шарика, можно найти вязкость данной жидкости.
Слайд 39: 3. Ротационные вискозиметры -
в которых жидкость находится в зазоре между двумя соосными тела-ми, например цилиндрами. Один из цилиндров (ротор) вращается, дру-гой неподвижен. Вязкость измеряет-ся по угловой скорости ротора, соз-дающего определенный момент силы на неподвижном цилиндре,