Дисперсионный анализ (от латинского Dispersio – рассеивание / на английском Analysis Of Variance - ANOVA) применяется для исследования влияния одной или нескольких качественных переменных ( факторов-качественные, количественные, случайные ) на одну зависимую количественную переменную ( отклик ). В дисперсионном анализе используется свойство аддитивности дисперсии независимых факторов. Р.А.Фишер в 1938 году впервые определил дисперсионный анализ как «отделение дисперсии, приписываемой одной группе причин, от дисперсии, приписываемой другим группам» Дисперсионный анализ состоит в выделении и оценке отдельных факторов, вызывающих изменчивость изучаемой случайной величины. Для этого проводят разложение суммарной дисперсии на составляющие, обусловленные независимыми факторами. .
Проверка значимости оценок дисперсий проводиться по F- критерию Фишера: применяют для сравнения двух независимых нормально распределенных выборочных совокупностей. Выборочные дисперсии, различаются значимо, если частное превышает табличный F кр критерий Фишера для принятой доверительной вероятности p и чисел степеней свободы f 1 =n 1 -1, f 2 =n 2 -1.
Допущения в дисперсионном анализе: 1.случайные ошибки наблюдений имеют нормальное распределение; где и - математическое ожидание и генеральная дисперсия случайной величины Х. 2.факторы влияют только на изменение средних значений, а дисперсия наблюдений остается постоянной; эксперименты равноточны.
Факторы, рассматриваемые в дисперсионном анализе, бывают двух родов: 1) со случайными уровнями (выбор уровней производится из бесконечной совокупности возможных уровней - модель со случайными уровнями факторов ); 2) с фиксированными (все уровни фиксированы – модель с фиксированными уровнями факторов); 3) модель смешанного типа (часть факторов рассматривается на фиксированных уровнях, а уровни остальных выбираются случайным образом).
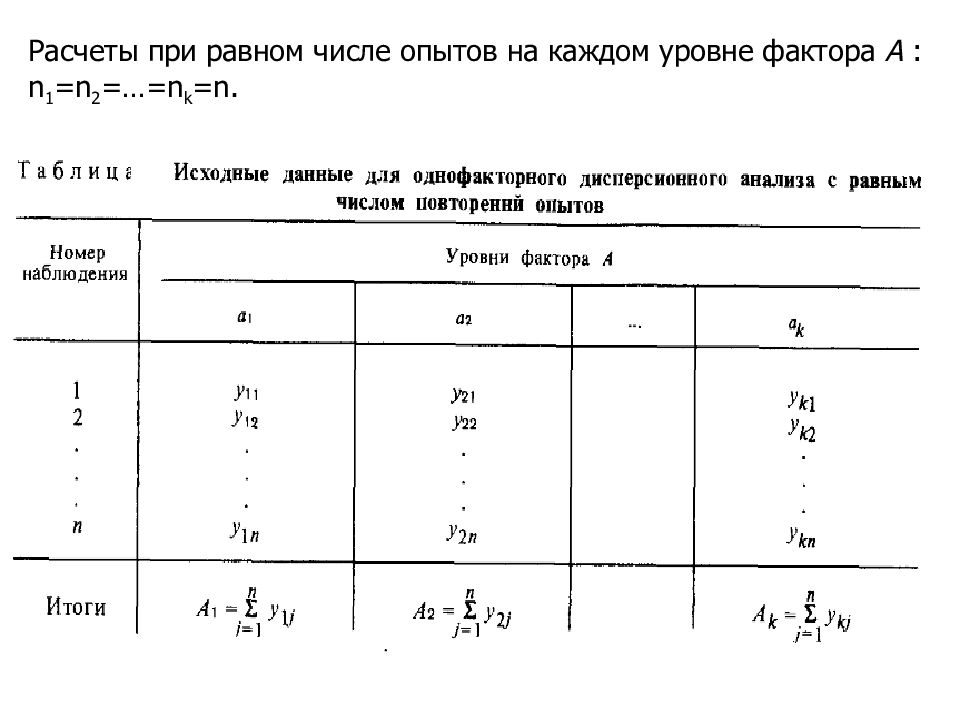
Задачей однофакторного дисперсионного анализа является изучение влияния одного фактора А (количественного или качественного), который принимает k различных значений (уровней факторов), на рассматриваемый признак (отклик). На i -м уровне производиться n i н аблюдений, результаты которых представлены:
где μ - суммарный эффект во всех опытах; d i - эффект фактора А на i - м уровне ( i = 1,2,…, k ); - ошибка измерения на i - м уровне. Предположим, что наблюдения на фиксированном уровне фактора нормально распределены относительно среднего значения с обшей дисперсией Проверяется нулевая гипотеза равенства средних значений на различных уровнях фактора А : m 1 =m 2 =…=m k =m. Общее число опытов равно N : N=n 1 +n 2 +…+n k.
Расчеты при равном числе опытов на каждом уровне фактора А : n 1 =n 2 =…=n k =n.
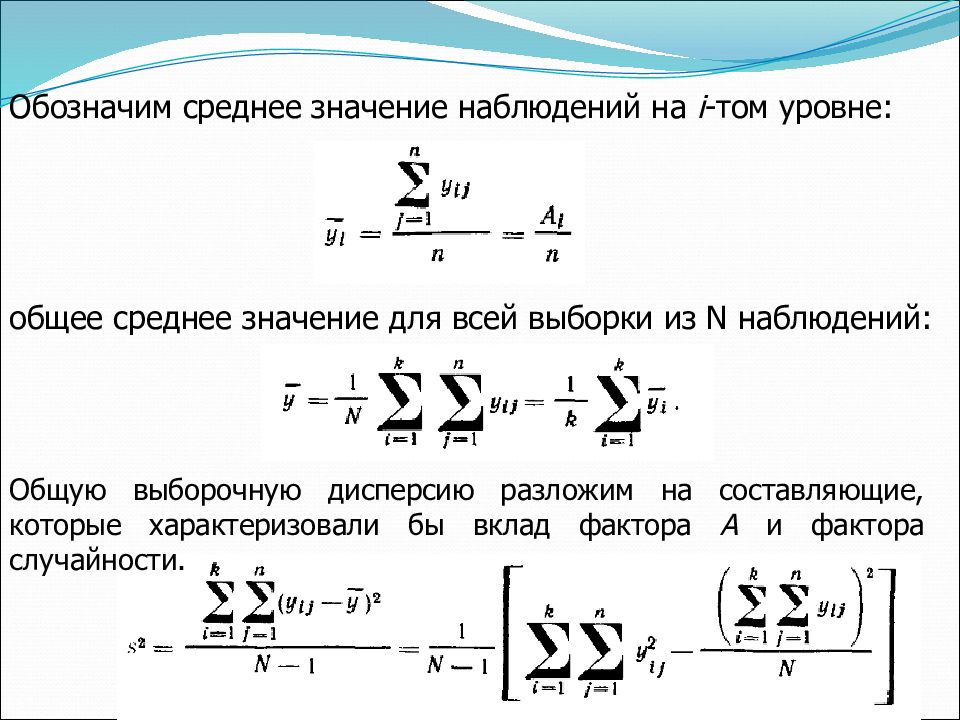
Обозначим среднее значение наблюдений на i -том уровне: общее среднее значение для всей выборки из N наблюдений: Общую выборочную дисперсию разложим на составляющие, которые характеризовали бы вклад фактора А и фактора случайности.
Определим выборочную дисперсию на каждом уровне: Критерий Кохрана (проверка однородности системы) применяют для сравнения k независимых нормально распределенных выборочных совокупностей равных объемов n i = const с дисперсиями. Выборочные дисперсии различаются значимо, если критерий Кохрана G превышает табличный G кр для принятой доверительной вероятности p и числа степеней свободы f=k-1.
Если между выборочными дисперсиями нет значимых различий, для оценки генеральной дисперсии σ 2, характеризующей фактор случайности, используют выборочную дисперсию S ош 2 : ( f=k(n-1)=N-k ). Приближенную оценку для дисперсии фактора А можно получить следующим образом: Более точную оценку для можно получить, рассматривая отклонения средних на отдельных уровнях от общего среднего всей выборки.
Введем следующее обозначение, дисперсия фактора А (проверка нулевой гипотезы по критерию Фишера): Влияние фактора является значимым, если:
Алгоритм: 1) итоги по столбцам 2) сумму квадратов всех наблюдений 3) сумму квадратов итогов по столбцам, деленную на число наблюдений в столбце 4 ) квадрат общего итога, деленный на число всех наблюдений (корректирующий член) 5) сумма квадратов для столбца 6) SS общ - общая сумма квадратов, равная разнице между суммой квадратов всех наблюдений и корректирующим членом
8) дисперсия 9) дисперсия 7) SS ост - остаточная сумма квадратов для оценки ошибки эксперимента
Результаты расчета представляются в виде таблицы дисперсионного анализа. Если неравенство, справедливо, то различие между и значимо, следовательно значимо влияние фактора А.
Если выборочные дисперсии различаются в пределах случайного разброса, то следующим шагом является сравнение выборочных средних. Выборочные средние различаются значимо, если t- критерий Стьюдента превышает табличный t p, f для принятой доверительной вероятности p и числа степеней свободы объединенной выборки f=n 1 +n 2 -2. Нулевая гипотеза отвергается и различие между средними считается значимым. Для выявления различности средних применяют критерии Стьюдента, Фишера или ранговый критерий Дункана.
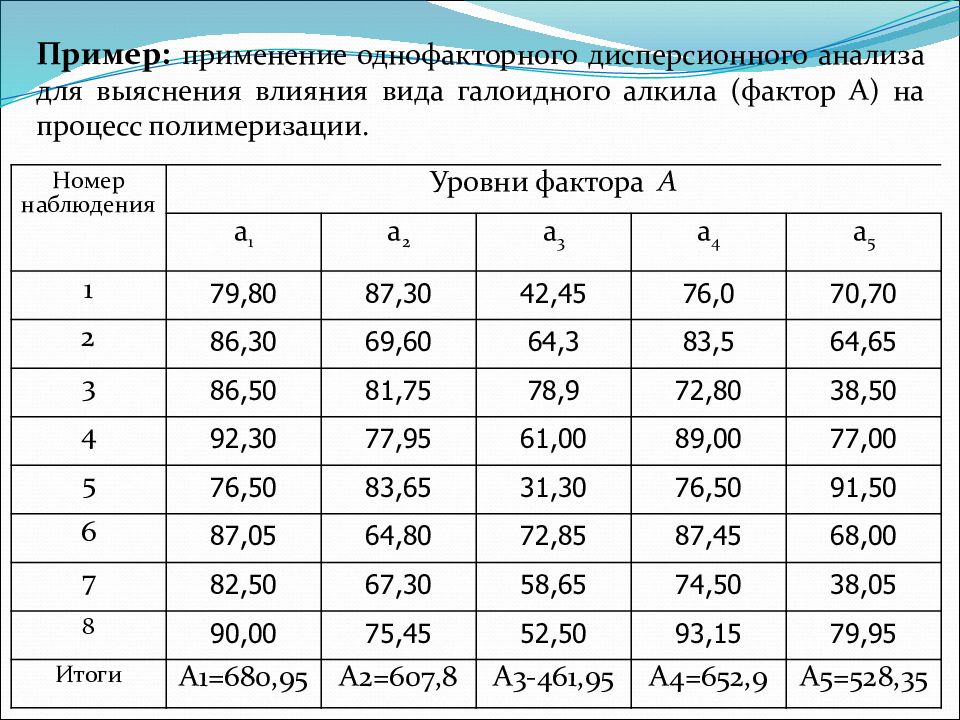
Номер наблюдения Уровни фактора А а 1 а 2 а 3 а 4 а 5 1 79,80 87,30 42,45 76,0 70,70 2 86,30 69,60 64,3 83,5 64,65 3 86,50 81,75 78,9 72,80 38,50 4 92,30 77,95 61,00 89,00 77,00 5 76,50 83,65 31,30 76,50 91,50 6 87,05 64,80 72,85 87,45 68,00 7 82,50 67,30 58,65 74,50 38,05 8 90,00 75,45 52,50 93,15 79,95 Итоги А1=680,95 А2=607,8 А3-461,95 А4=652,9 А5=528,35 Пример: применение однофакторного дисперсионного анализа для выяснения влияния вида галоидного алкила (фактор А) на процесс полимеризации.
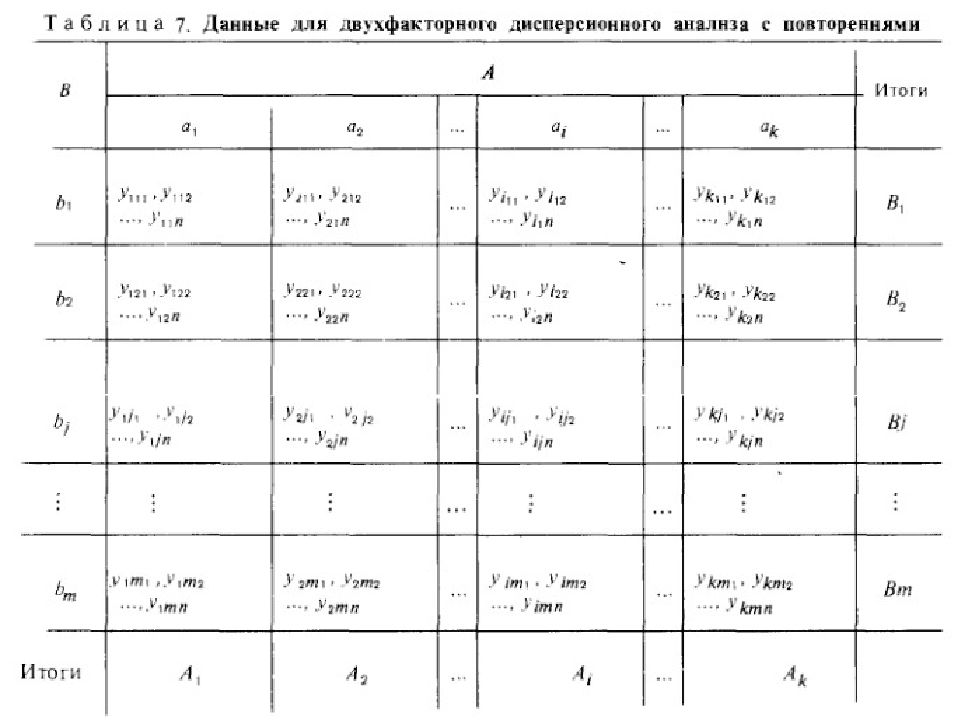
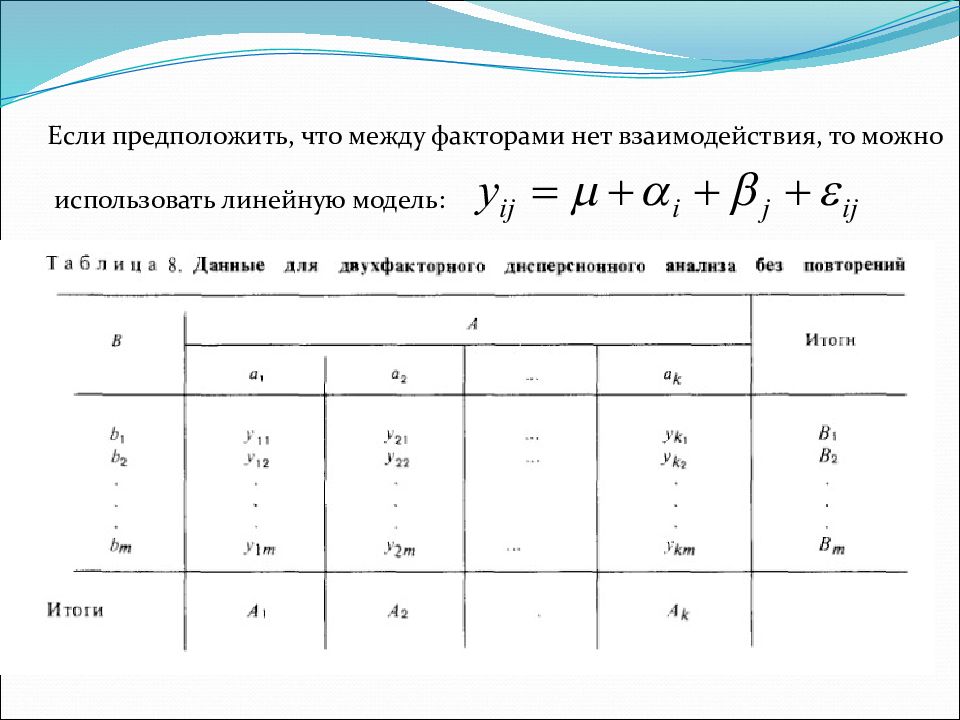
Изучается влияние на процесс одновременно двух факторов А и В. Фактор А исследуется, на уровнях a 1, a 2,…, a k. Фактор В – на уровнях b 1,b 2,…,b m.
Общее число наблюдений равно N=nkm Общее среднее; эффект фактора А на i - м уровне, i =1,2,…, K ; эффект фактора В на j- м уровне, j =1,2,… m ; эффект взаимодействия факторов, представляем собой отклонение среднего по наблюдениям в ( ij ) - й серии от суммы первых- трех членов в модели учитывает вариацию внутри серии наблюдений (ошибка воспроизводимости)
Если предположить, что между факторами нет взаимодействия, то можно использовать линейную модель:
Линейная модель: Через и обозначим соответственно средние значения по строкам и столбцам: А - среднее всех результатов Рассеяние средних по столбцам относительно общего среднего не зависит от фактора В, т.к. все уровни фактора В усреднены. Это рассеяние связано с влиянием фактора А и случайного фактора. Так как дисперсия среднего в m раз меньше дисперсии единичного измерения, имеем:
В свою очередь, рассеяние в средних по строкам на зависит от фактора А и связано с влиянием фактора В: Эти равенства позволяют оценить влияние факторов А и В, если известна оценка дисперсии. Линейная модель: Для оценки фактора случайности при отсутствии параллельных наблюдений, найдем дисперсию наблюдений по i -му столбцу: (б) (а)
Эта дисперсия обусловлена влиянием фактора В и фактора случайности Вычитая (б) из (а), получим Отсюда Обозначим полученную оценку для дисперсии σ 2 через S ош 2
Введем следующие обозначения: Величины и можно считать выборочными дисперсиями с (к-1) и ( m -1) степенями свободы соответственно. Проверяют нулевые гипотезы о незначимости влияния факторов А и В по критерию Фишера. Нулевая гипотеза значима, α i =0.
Если нулеваая гипотеза отвергается и влияние фактора А считается значимым. Аналогично, если Гипотеза принимается, βj =0. При справедливости неравенства: Влияние фактора В считается значимым.
При проведении дисперсионного анализа в условиях линейной модели, используют следующий алгоритм расчета: Находят : Итоги по столбцам Итоги по строкам Сумму квадратов всех наблюдений Сумму квадратов итогов по столбцам, деленную на число наблюдений в столбце
5) Сумму квадратов итогов по строкам., деленную на число наблюдений в строке 6) Квадрат общего итога, деленный на число всех наблюдений (корректирующий член) 7) Сумму квадратов для столбца: SS A =SS2-SS4 ; 8) Сумму квадратов для строки: SS B =SS3-SS4 ; 9) Общую сумму квадратов, равную разнице между суммой квадратов всех наблюдений и корректирующим членом: SS общ =SS1-SS4 ; 10) Остаточную сумму квадратов: SS ост =SS общ -SS A -SS B =SS1-SS2-SS3+SS4 ;
11) Дисперсию : 12) Дисперсию : 13) Дисперсию :
Рассмотрим модель со взаимодействием факторов А и В. Пусть при каждом сочетании уровней факторов А и В проводится n параллельный опытов. Имеется целая серия наблюдений y i j1, y ij2,…, y ijn. Выборочная дисперсия результатов в каждой ячейке, где ( n-1 ) - степень свободы: Если выборочные дисперсии по всем ячейкам однородны, их можно усреднить и использовать полученную средневзвешенную дисперсию в качестве оценки для дисперсии воспроизводимости σ 2 : Число степеней свободы равно mk (n-1)
Более удобная формула для вычисления дисперсии воспроизводимости где y ij - сумма наблюдений в ij – й ячейке.
При проведении дисперсионного анализа в условиях модели с учетом взаимодействия факторов А и В, удобно использовать следующий алгоритм расчета:
7) Сумму квадратов итогов по столбцам, деленную на число наблюдений в столбце 8) Сумму квадратов итогов по строкам., деленную на число наблюдений в строке
9) Квадрат общего итога, деленный на число всех наблюдений (корректирующий член) 10) Сумму квадратов для столбца 11)Сумму квадратов для строки 12) Сумму квадратов для дисперсии воспроизводимости 13) Общую сумму квадратов, равную разнице между суммой квадратов всех наблюдений и корректирующим членом
14) Остаточную сумму квадратов отклонений для эффекта взаимодействия АВ
Для оценки значимости фактора А необходимо составить дисперсионное отношение вида
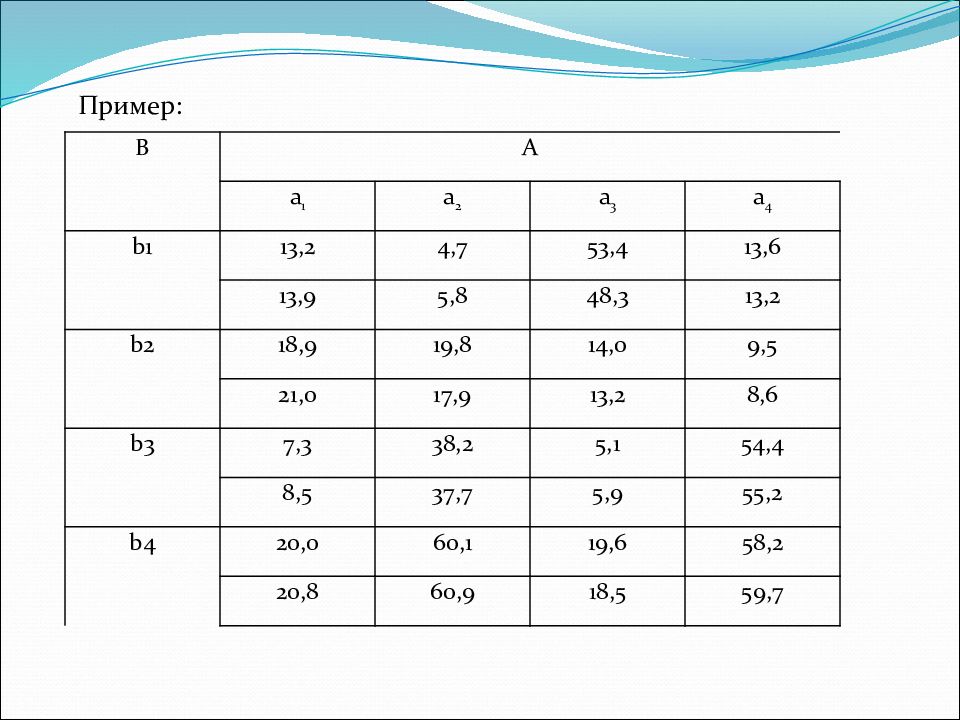
Пример: В А а 1 а 2 а 3 а 4 b1 13,2 4,7 53,4 13,6 13,9 5,8 48,3 13,2 b2 18,9 19,8 14,0 9,5 21,0 17,9 13,2 8,6 b3 7,3 38,2 5,1 54,4 8,5 37,7 5,9 55,2 b4 20,0 60,1 19,6 58,2 20,8 60,9 18,5 59,7
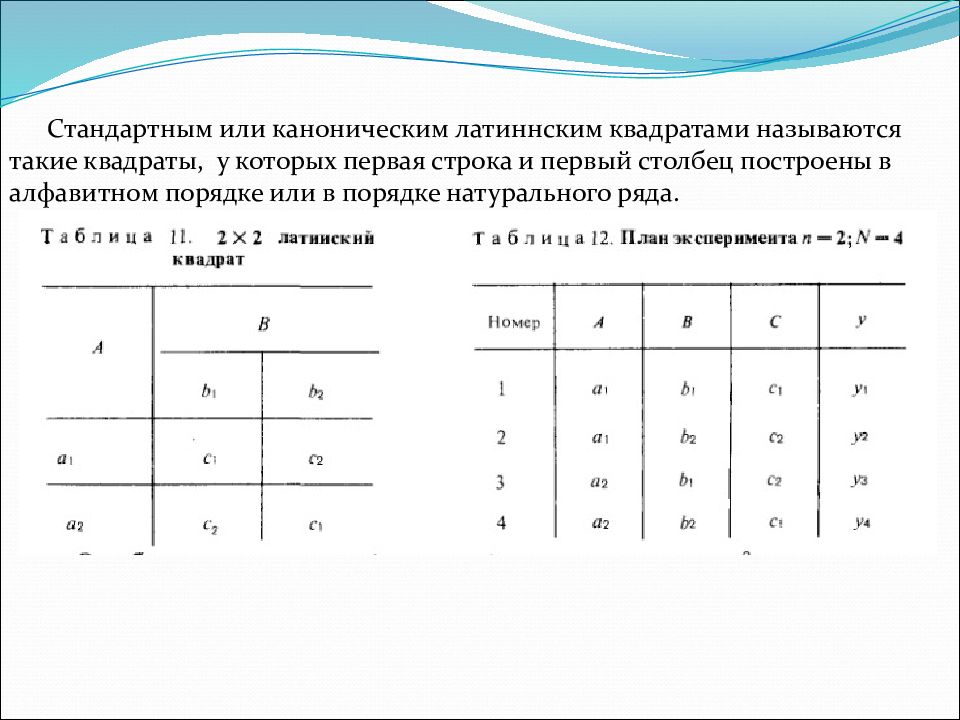
Латинские и гипер-греко-латинские квадраты. Полным факторным экспериментом(ПФЭ) называют эксперимент, в котором встречаются все возможные сочетания уровни изучаемых факторов. Дробным факторным экспериментом(ДФЭ) – эксперимент, в котором пропущены некоторые сочетания уровней. Рассмотрим трехфакторный дисперсионный анализ при одинаковом числе уровней n для каждого фактора. Полный перебор сочетаний уровней факторов потребует N опытов N=n 3 Число опытов можно значительно сократить, используя ДФЭ по схеме латинского квадрата, введенного впервые Фишером. Латинский квадрат – n : n – это квадратная матрица, составленная из n элементов(чисел или букв) таким образом, что каждый элемент повторяется в каждой строке и в каждом столбце только один раз.
Стандартным или каноническим латиннским квадратами называются такие квадраты, у которых первая строка и первый столбец построены в алфавитном порядке или в порядке натурального ряда.
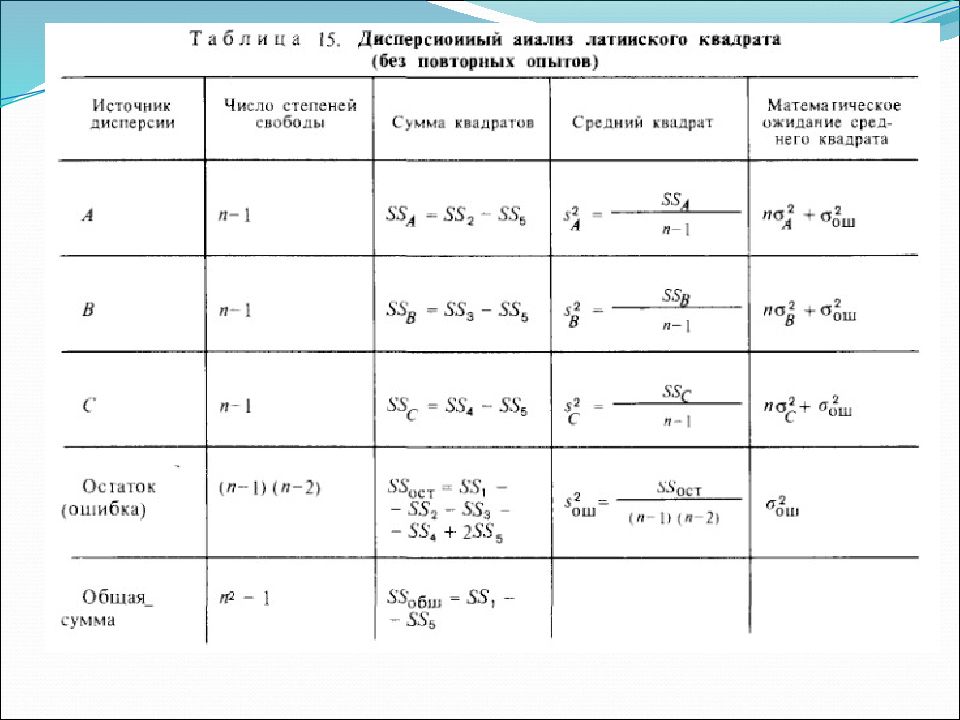
Результат наблюдения, полученный при ПФЭ При применении латинского квадрата предполагают, что результаты взаимодействия незначимы и применяют линейную модель Алгоритм расчета: Для этого определяют 1) итоги по строкам А i, столбцам В j, и латинским буквам С q. Например, для латинского квадрата 3:3 итоги по строкам Итоги по столбцам
Итоги по латинским буквам 3) Сумму квадратов итогов по строкам, деленную на число наблюдений в строке 4) Сумму квадратов итогов по столбцам, деленную на число наблюдений в столбце
5)Сумму квадратов итогов по латинским буквам, деленную на число наблюдений, соответствующих каждой букве 6) Квадрат общего итога, деленный на число всех наблюдений(корректирующий член) 10) Общую сумму квадратов, равную разнице между суммой квадратов всех наблюдений и корректирующим членом
