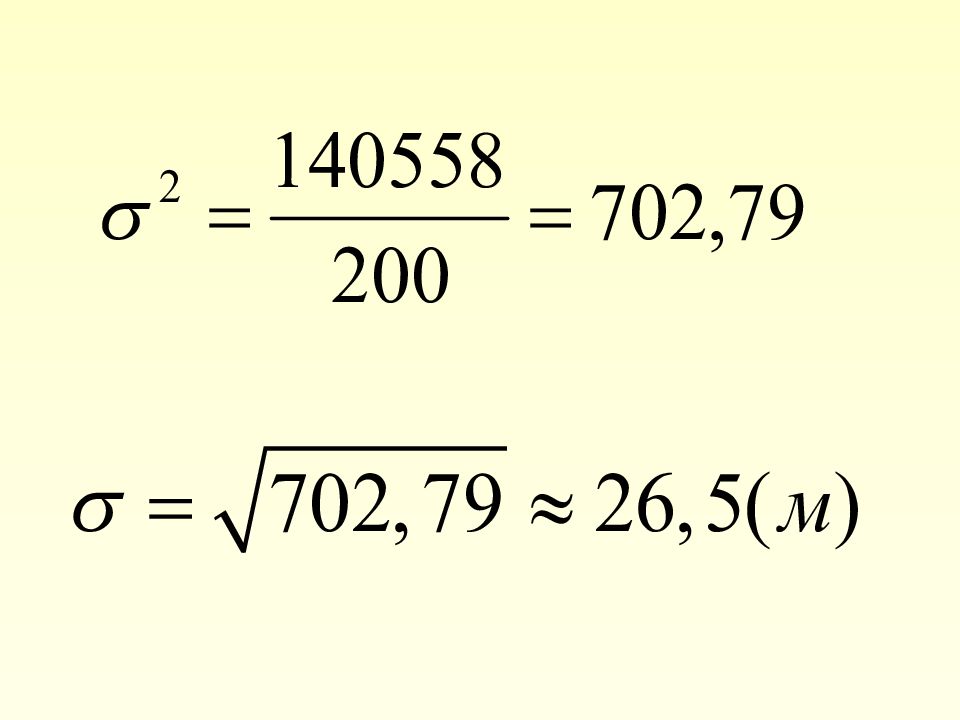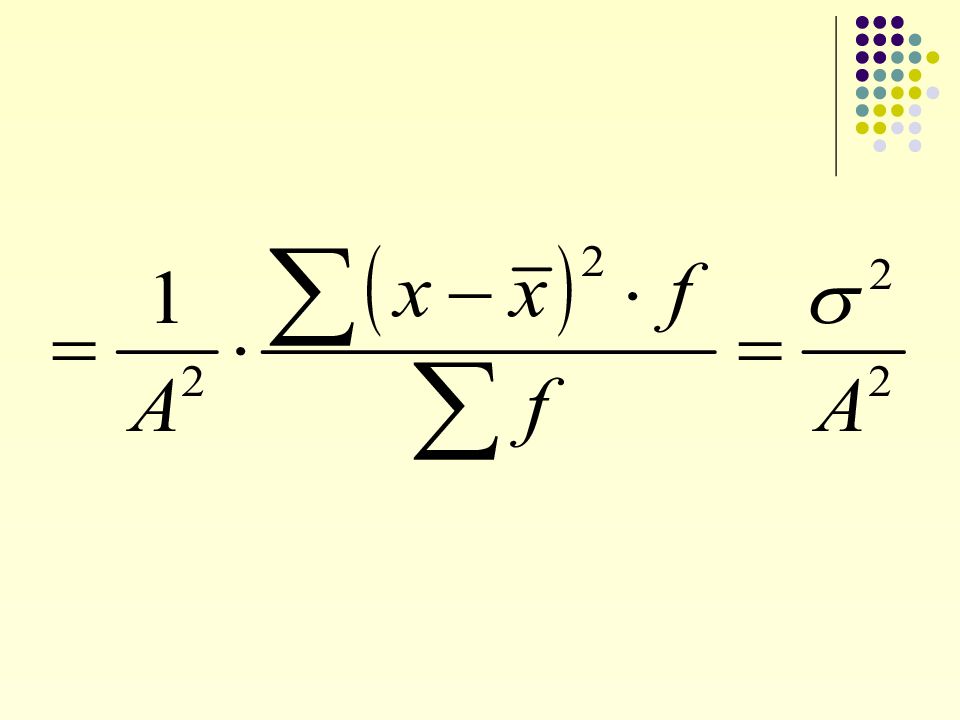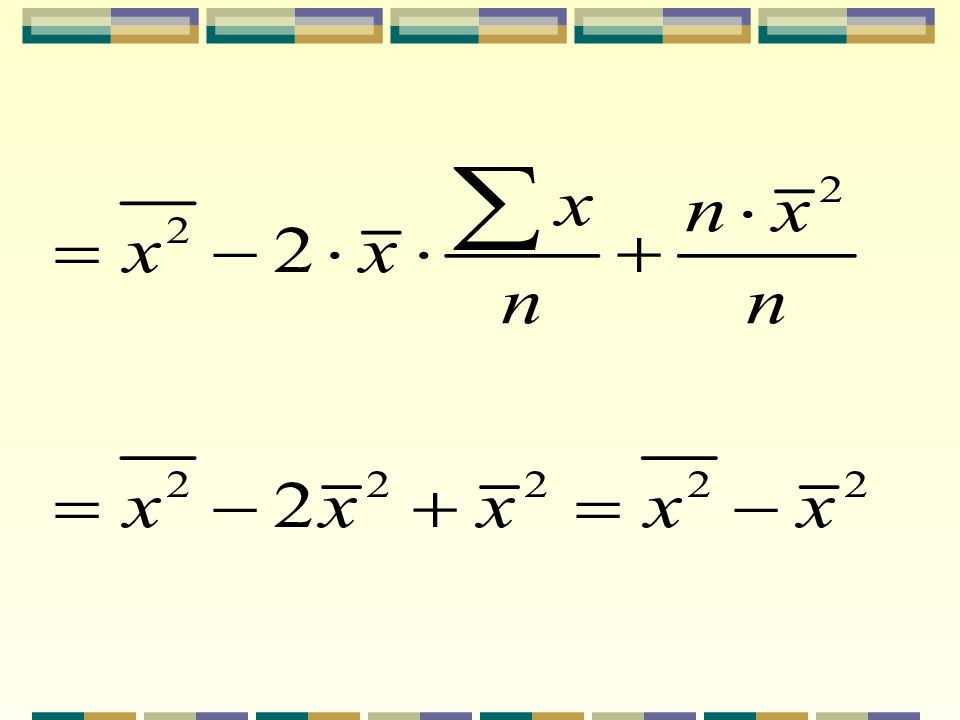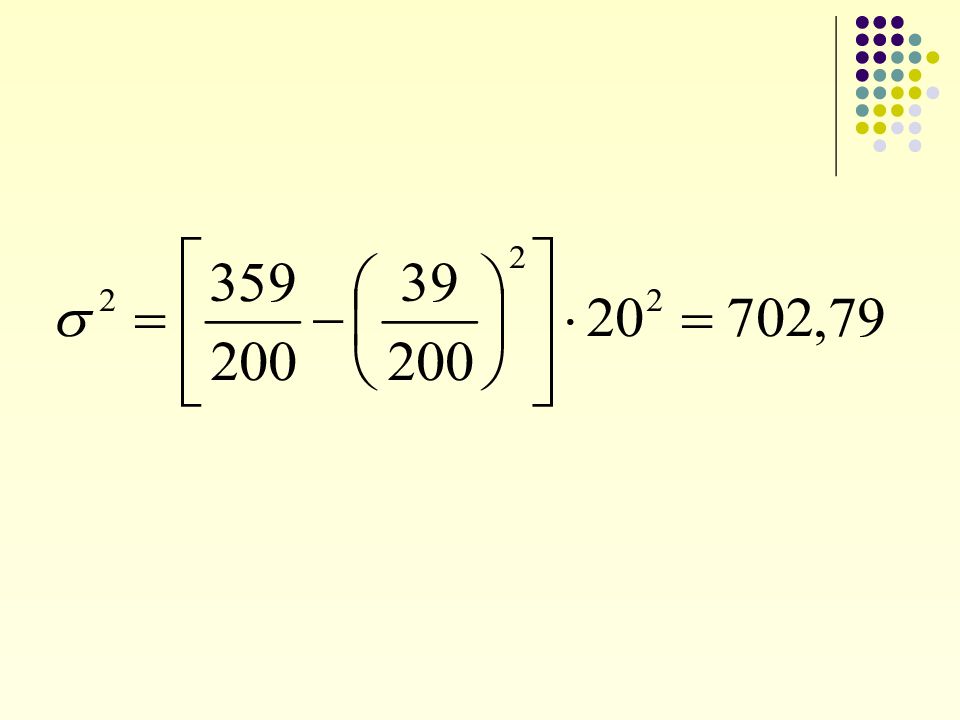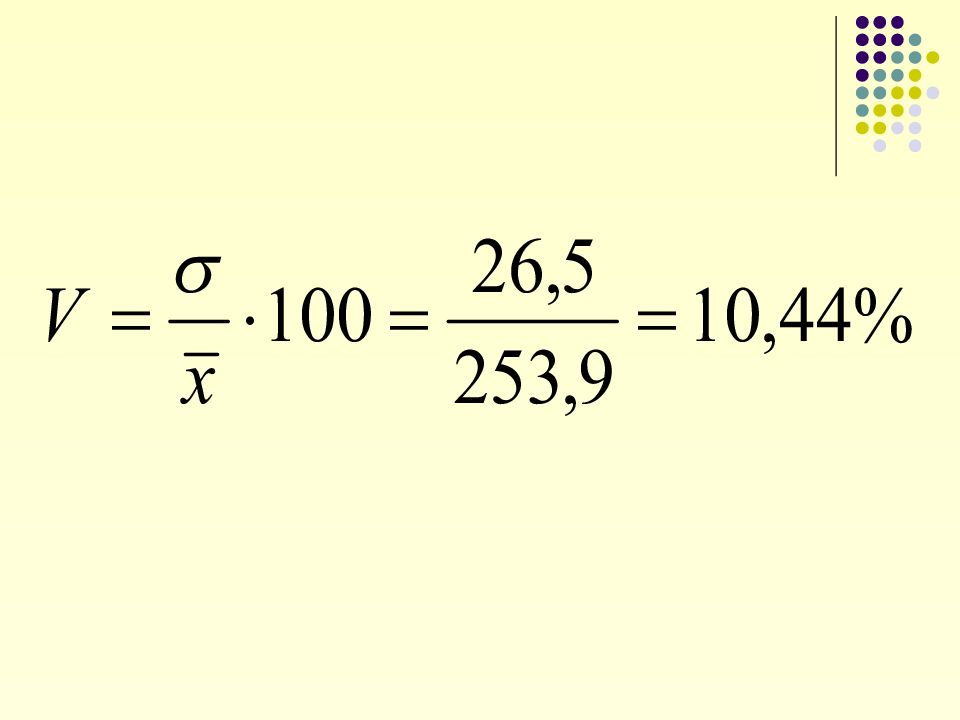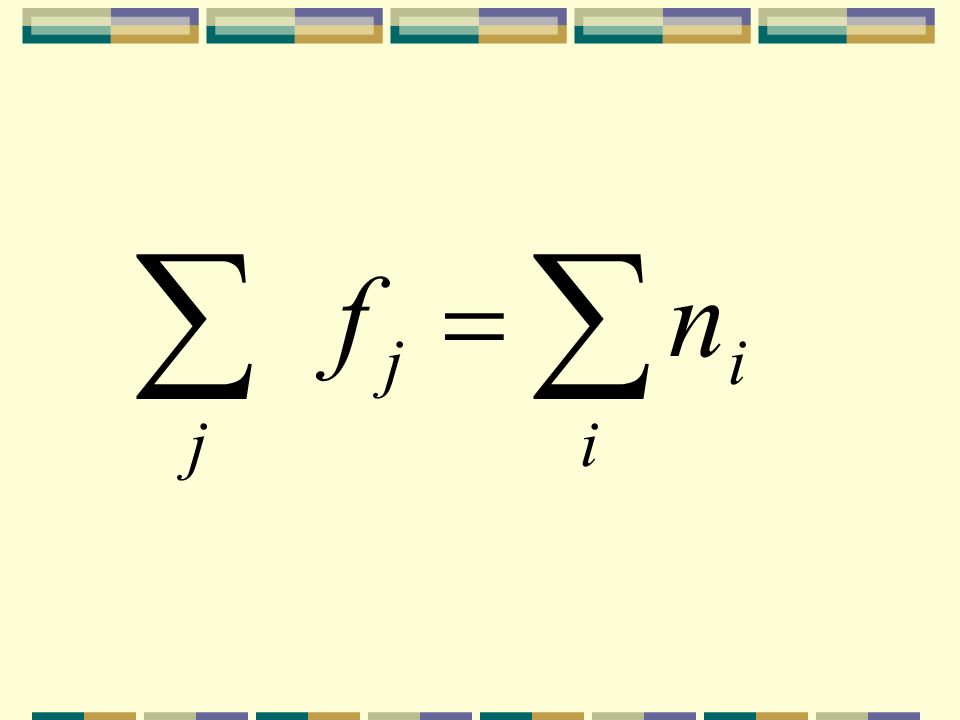Показатели вариации
Средняя величина характеризует совокупность по изучаемому признаку, такой характеристики совокупности будет достаточно, если разброс индивидуальных значений невелик Когда ряд характеризуется значительным рассеиванием индивидуальных значений, то применение средней величины ограничено
Вариацией называется изменчивость значений признака у единиц статистической совокупности
При значительном рассеивании индивидуальных значений необходимо рассчитать специальную систему показателей, характеризующих средний размер отклонений индивидуальных значений от средней величины и степень колеблемости признака в совокупности, т.е. показателей вариации
Используются две группы показателей вариации: - абсолютные: размах вариации, среднее линейное отклонение, дисперсия, среднеквадратическое отклонение - относительные: коэффициент осцилляции, линейный коэффициент и коэффициент вариации
РВ – разность между экстремальными значениями признака в совокупности. РВ имеет единицу измерения, совпадающую с единицей измерения признака у единиц совокупности
Недостаток РВ: он учитывает только крайние значения и не учитывает промежуточные значения
Недостаток РВ устраняет показатель СЛО. Он рассчитывается по двум формулам: а) для несгруппированных данных (по формуле средней арифметической простой) б ) для сгруппированных данных (по формуле средней арифметической взвешенной)
а) для несгруппированных данных б ) для сгруппированных данных
У СЛО есть единица измерения. Он обладает серьезным недостатком : в числителе нет минуса, а сам показатель – положительное число. Эта проблема решается третьим и четвертым показателями вариации – дисперсией и среднеквадратическим отклонением
3. Дисперсия - средний квадрат отклонений индивидуальных значений от средней величины. Это средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней. Она рассчитывается по простой и взвешенной формулам. Для ее обозначения используется греческая буква сигма.
Дисперсия а) для несгруппированных данных б ) для сгруппированных данных
Расчет дисперсии для вариационного ряда
Осуществляется при помощи взвешенной формулы:
1.Если из всех вариант вычесть какую-либо константу, то дисперсия от этого не изменится:
2.Если все варианты разделить на константу А, то дисперсия уменьшится от этого в А² раз:
3. Дисперсия равна разности среднего квадрата вариант и квадрата их средней:
4. Если рассчитать среднее квадратическое отклонение от любой константы А, отличной от средней арифметической, то оно всегда будет больше дисперсии на квадрат разности между средней и данной константой А: , где
Расчет дисперсии упрощенным способом
Расчет дисперсии упрощенным способом осуществляется на основе перечисленных свойств по формуле: , где
Недостаток дисперсии состоит в том, что она имеет размерность вариант, возведенную в квадрат (рублей в квадрате, человек в квадрате) Чтобы устранить этот недостаток, используется среднее квадратическое отклонение
4.Среднее квадратическое отклонение а) для несгруппированных данных
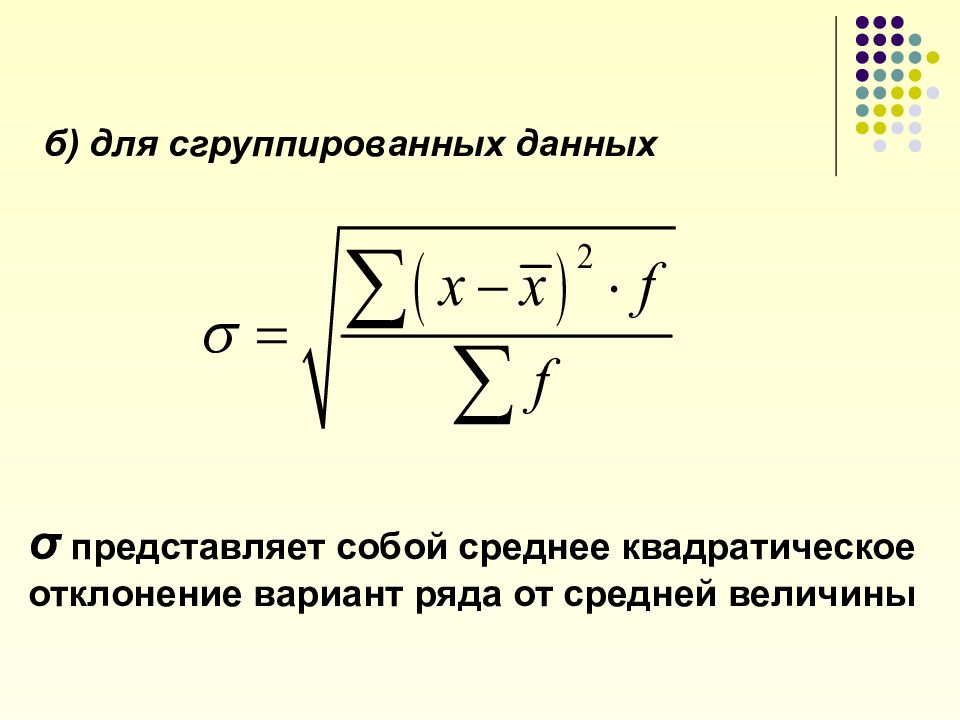
б) для сгруппированных данных σ представляет собой среднее квадратическое отклонение вариант ряда от средней величины
Среднее квадратическое отклонение имеет единицы измерения, а также может принимать положительные и отрицательные значения, поскольку получается в результате извлечения квадратного корня. С помощью СКО можно утверждать, что i - тое значение признака в совокупности находится в пределах:
Относительные показатели вариации
Относительные показатели вариации применяются для решения следующих задач: - сравнение степени вариации различных вариационных рядов - характеристика степени однородности совокупности
Коэффициент осцилляции где R - размах вариации - среднее значение
Коэффициент осцилляции отражает относительную колеблемость крайних значений признака относительно среднего значения
Линейный коэффициент вариации (относительное линейное отклонение) где - среднее линейное отклонение
Коэффициент вариации Характеризует долю усредненного значения отклонений от средней величины. При этом совокупность считается однородной, если V не превышает 33%
При V > 33% совокупность неоднородна, для дальнейшего статистического анализа следует либо исключить крайние значения признака, либо разбить совокупность на однородные группы. Требование к однородности данных присутствует практически во всех видах статистического анализа -Салин, Чурилова, с. 142
Правило трех сигм
В условиях нормального распределения существует зависимость между величиной σ и количеством наблюдений: располагается 68,3 % наблюдений; располагается 94,5 % наблюдений; располагается 99,7 % наблюдений. в пределах в пределах в пределах
На практике почти не встречаются отклонения, которые превышают 3σ. Отклонение в 3σ может считаться максимальным При помощи этого правила можно получить примерную оценку σ:
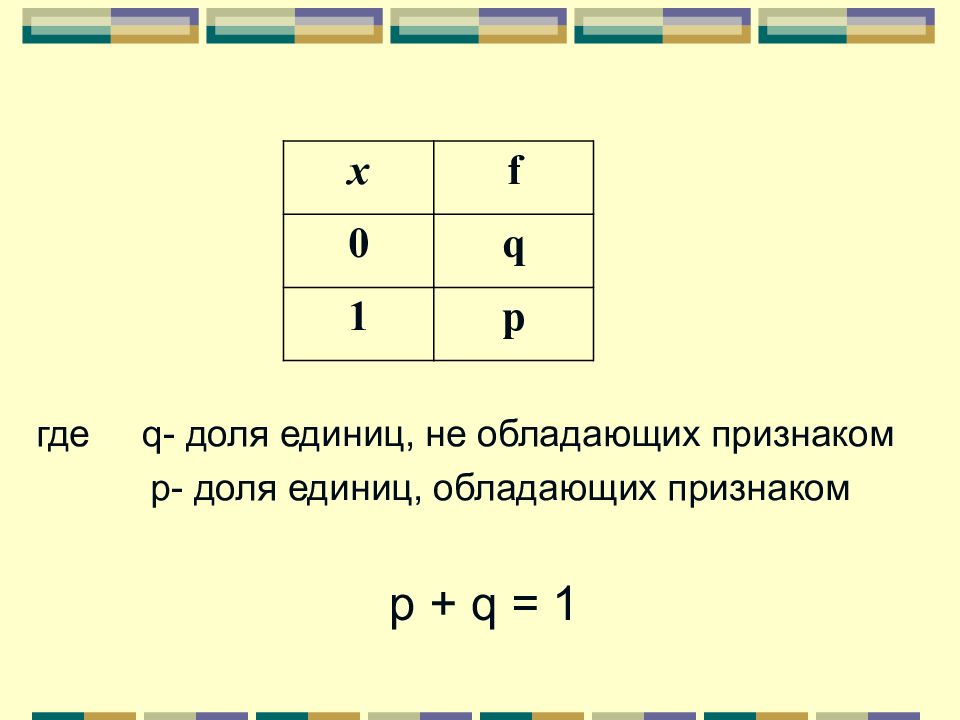
Признаки, которыми обладают одни единицы совокупности и не обладают другие, называются альтернативными. Количественно вариация альтернативного признака проявляется в значении 0 у единиц, которые им не обладают, или в значении 1 у единиц, которые им обладают
x f 0 q 1 p где q - доля единиц, не обладающих признаком p - доля единиц, обладающих признаком p + q = 1
Дисперсия альтернативного признака : Максимальное значение дисперсии альтернативного признака 0,25
Среднее квадратическое отклонение альтернативного признака : Коэффициент вариации альтернативного признака:
Правило сложения дисперсий
1) общую 2) межгрупповую 3) внутригрупповую Выделяют дисперсии:
Величина общей дисперсии характеризует вариацию признака под воздействием всех факторов, вызывающих эту вариацию: где j – номер варианты
Межгрупповая дисперсия (дисперсия групповых средних или факторная дисперсия) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием одного фактора, положенного в основание группировки
где – среднее значение изучаемого признака для i – й группы – общая средняя для всей совокупности - номер группы – количество единиц в i – й группе
Внутригрупповая (средняя из групповых или остаточная) дисперсия характеризует случайную вариацию, т. е. ту часть вариации, которая вызвана действием других неучтённых факторов, и не зависящую от фактора, положенного в основании группировки:
где - групповая дисперсия
Общая дисперсия равна сумме межгрупповой и внутригрупповой дисперсий:
Эмпирический коэффициент детерминации: Эмпирический коэффициент детерминации показывает долю общей вариации изучаемого признака, обусловленную вариацией группировочного признака (факторного)
Эмпирическое корреляционное отношение : Эмпирическое корреляционное отношение характеризует степень влияния группировочного признака на результативный показатель. Эмпирическое корреляционное отношение изменяется в пределах от 0 до 1. Чем ближе η к единице, тем степень влияния больше 0 ≤ η ≤ 1
Моменты распределения
Обобщающие характеристики вариационного ряда могут быть представлены системой величин, носящих название моментов распределения
Формула момента k -го порядка: где: x – варианты k – показатель степени f – частоты А – const
1. При А = 0 получаем систему начальных моментов. Начальный момент k -го порядка выражается формулой: Начальный момент первого порядка равен
2. При А = получаем систему центральных моментов. Центральный момент k -го порядка выражается формулой: Центральный момент первого порядка равен 0 Центральный момент второго порядка равен σ²
При А = получаем систему условных моментов: где: – некоторый вариант ряда, обычно близкий к его середине
Нормированный момент представляет собой отношение центрального момента k -го порядка к k -ой степени среднего квадратического отклонения:
Нормированный момент - первого порядка равен 0 - второго порядка равен 1 - третьего и четвертого порядков используется для характеристики асимметрии и эксцессов
Показатели асимметрии и эксцесса
Симметричным называется такое распределение, при котором варианты, равноотстоящие от средней, имеют равные частоты. Если распределение асимметрично, частоты вариантов, равноотстоящих от средней, не равны между собой
Для характеристики асимметрии используется нормированный момент третьего порядка: Если А = 0 распределение симметрично Если А > 1 имеет место правосторонняя асимметрия Если А < 1 имеет место левосторонняя асимметрия
Под эксцессом понимается степень островершинности распределения, при этом в качестве эталона берется нормальное распределение. Характеристикой эксцесса является нормированный момент четвертого порядка
Формула коэффициента эксцесса:
Для нормального распределения Е = 0. Для более островершинных распределений, чем нормальное, Е > 0, для более плосковершинных Е < 0
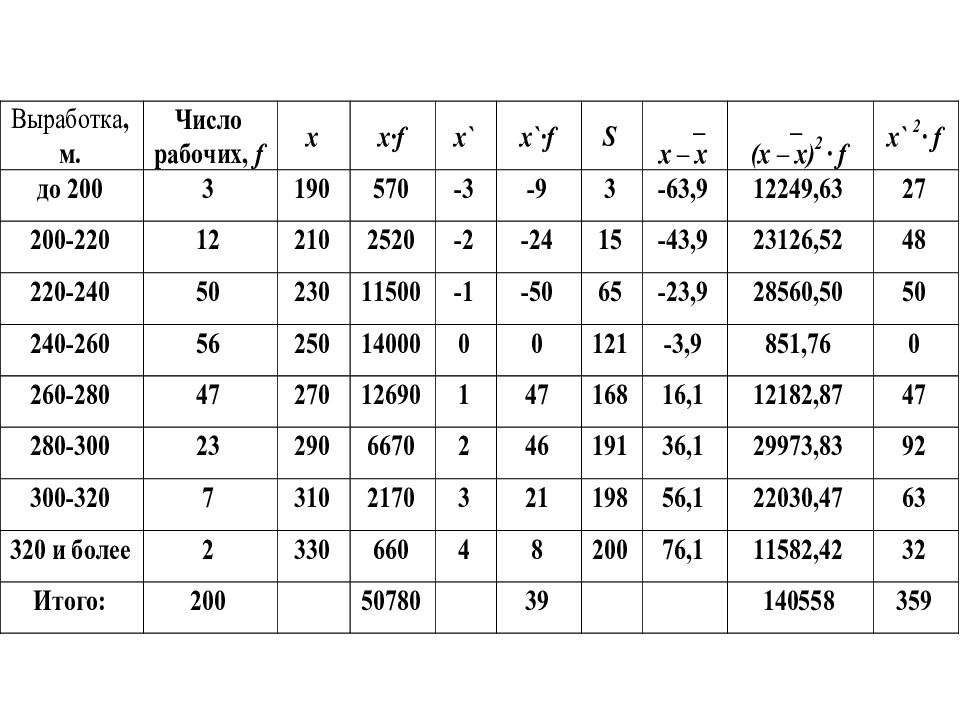
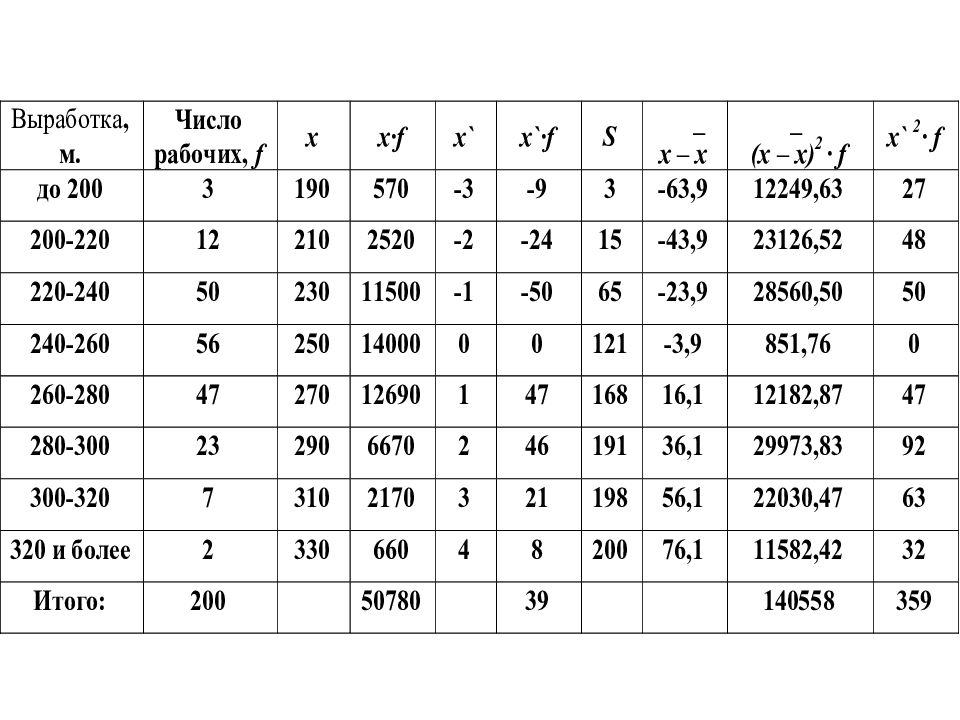
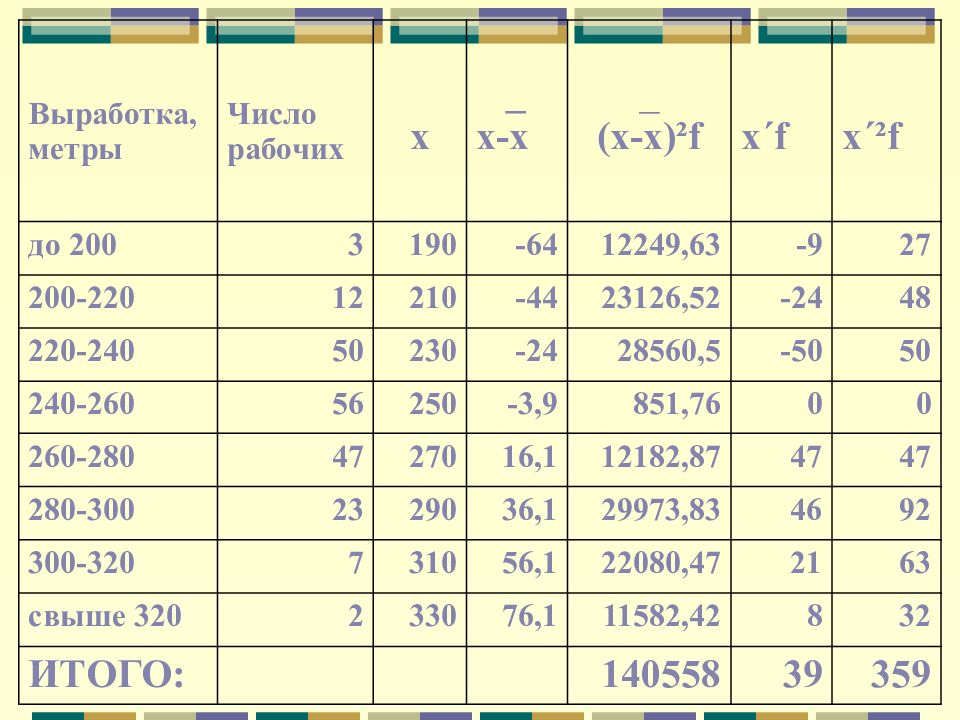
Выработка, метры Число рабочих х _ х-х _ ( x - x )² f х ΄f x΄ ² f до 200 3 190 -64 12249,63 -9 27 200-220 12 210 -44 23126,52 -24 48 220-240 50 230 -24 28560,5 -50 50 240-260 56 250 -3,9 851,76 0 0 260-280 47 270 16,1 12182,87 47 47 280-300 23 290 36,1 29973,83 46 92 300-320 7 310 56,1 22080,47 21 63 свыше 320 2 330 76,1 11582,42 8 32 ИТОГО: 140558 39 359
