Математическая статистика и ее роль в медицине и здравоохранении. Медико-демографические показатели
Предметом математической статистики является изучение случайных величин по результатам наблюдений. Для получения опытных данных необходимо провести обследование соответствующих объектов. Совокупность, которая включает в себя все изучаемые объекты, называется генеральной
Под статистическими данными понимаются сведения о числе объектов какой-либо обширной совокупности обладающими теми или иными признаками. На основании статистических данных можно сделать научно обоснованные выводы. Для этого статистические данные должны быть предварительно определенным образом систематизированы и обработаны.
Одним из основных методов обработки статистических данных является выборочный метод. При обработанном исследовании из всей совокупности выбирают некоторым образом определенное число объектов и только их подвергают исследованию. Совокупность всех исследуемых объектов называют генеральной совокупностью. Генеральную совокупность образуют, например, все больные с данным диагнозом, все новорожденные дети и тд. Общую сумму членов генеральной совокупности называют ее объемом и обозначают буквой N.
Выборкой называют совокупность случайно отобранных объектов из генеральной совокупности. Объем выборки будем обозначать буквой n. Число объектов выборки называют объемом выборки (например, из 10000 студентов для контрольной флюорографии отобраны 100 студентов, то объем генеральной совокупности равен 10000, а объем выборки равен100). Разность между наибольшим и наименьшим значениями числовой выборки называют размахом выборки. Выборку, представляющую собой неубывающую числовую последовательность, называют вариационным рядом. Любую числовую выборку можно записать в виде вариационного ряда.
Пример. Выборка: 1,10-2,0, 5-2,1,10,7 Вариационный ряд: -2, -2, 0, 1, 1, 5, 7, 10, 10 Объем выборки: n= 9 Размах выборки: 10-(-2) =12 Пусть из генеральной совокупности получена выборка объема n, причем n 1 раз, значение x 2 -n 2 раза и тд. в этом случае числа x 1, x 2,….., x n называют частотами значения выборки, а отношения, ……, относительными частотами значениями выборки : n 1 + n 2 + ……..+ n k = n …… +
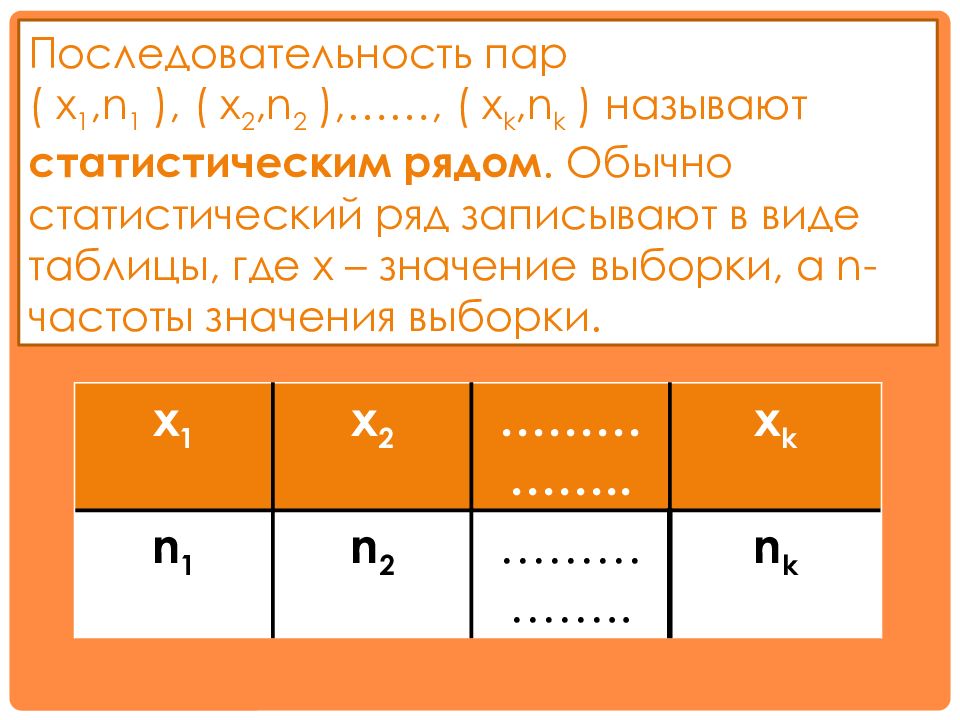
Последовательность пар ( x 1,n 1 ), ( x 2,n 2 ), ……, ( x k,n k ) называют статистическим рядом. Обычно статистический ряд записывают в виде таблицы, где x – значение выборки, а n- частоты значения выборки. x 1 x 2 …………….. x k n 1 n 2 …………….. n k
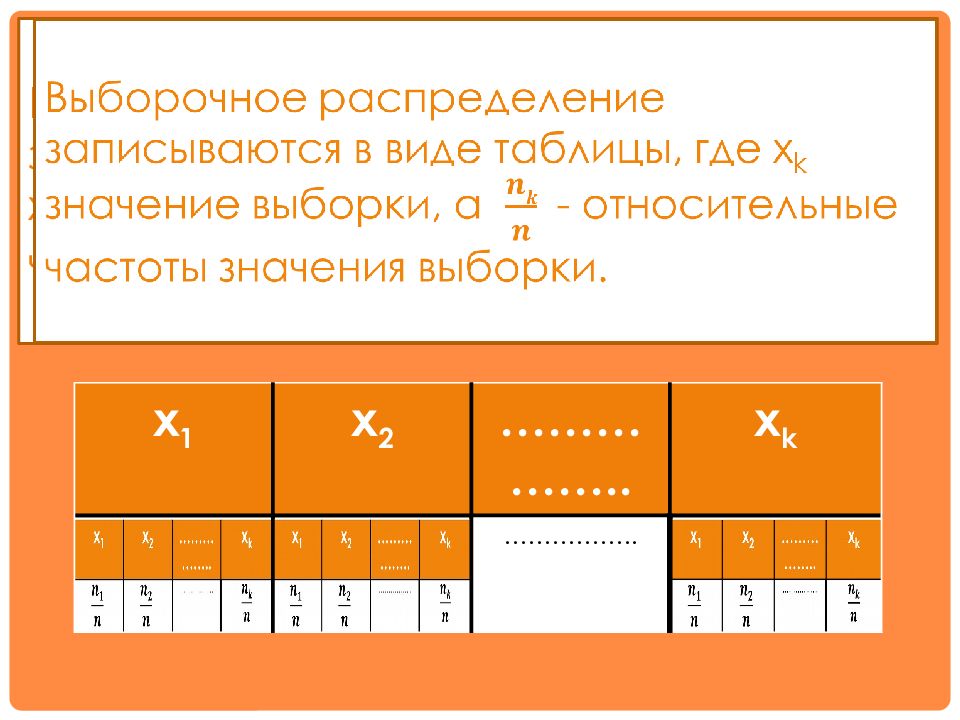
Выборочное распределение записываются в виде таблицы, где x k значение выборки, а - относительные частоты значения выборки. x 1 x 2 …………….. x k …………….. x 1 x 2 …………….. x k ……………..
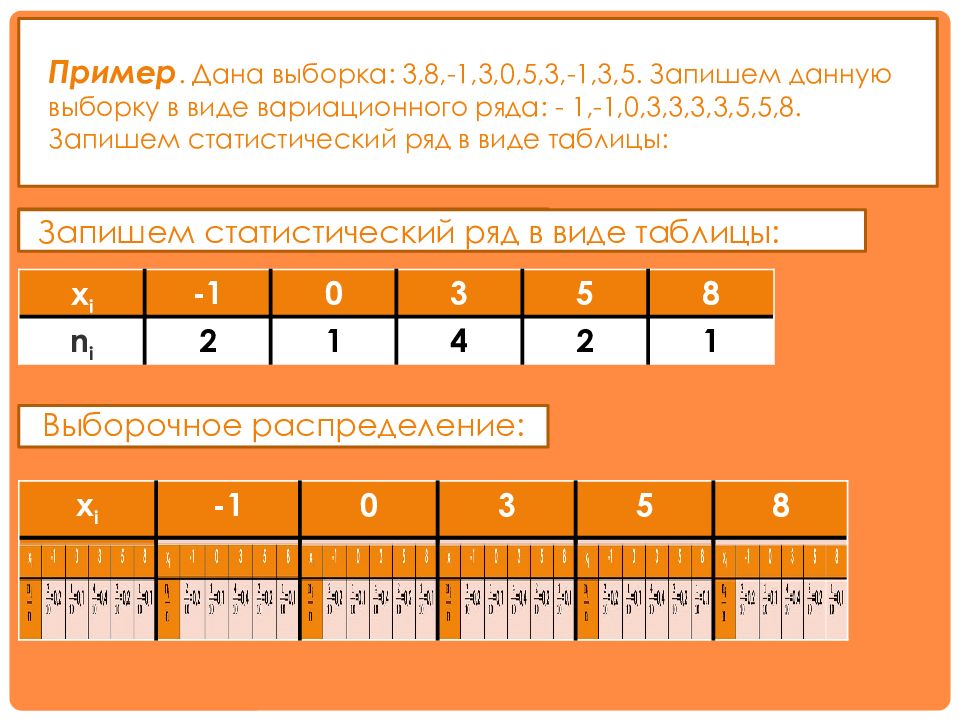
x i -1 0 3 5 8 n i 2 1 4 2 1 Пример. Дана выборка: 3,8,-1,3,0,5,3,-1,3,5. Запишем данную выборку в виде вариационного ряда: - 1,-1,0,3,3,3,3,5,5,8. Запишем статистический ряд в виде таблицы: Запишем статистический ряд в виде таблицы: Запишем статистический ряд в виде таблицы: Выборочное распределение: x i -1 0 3 5 8 =0,2 =0,1 =0,4 =0,2 =0,1 x i -1 0 3 5 8
Пусть имеется выборка объема n x 1, x 2,……, x n Выборочным математическим ожиданием (выборочным средним) называют среднее арифметическое выборки: = =
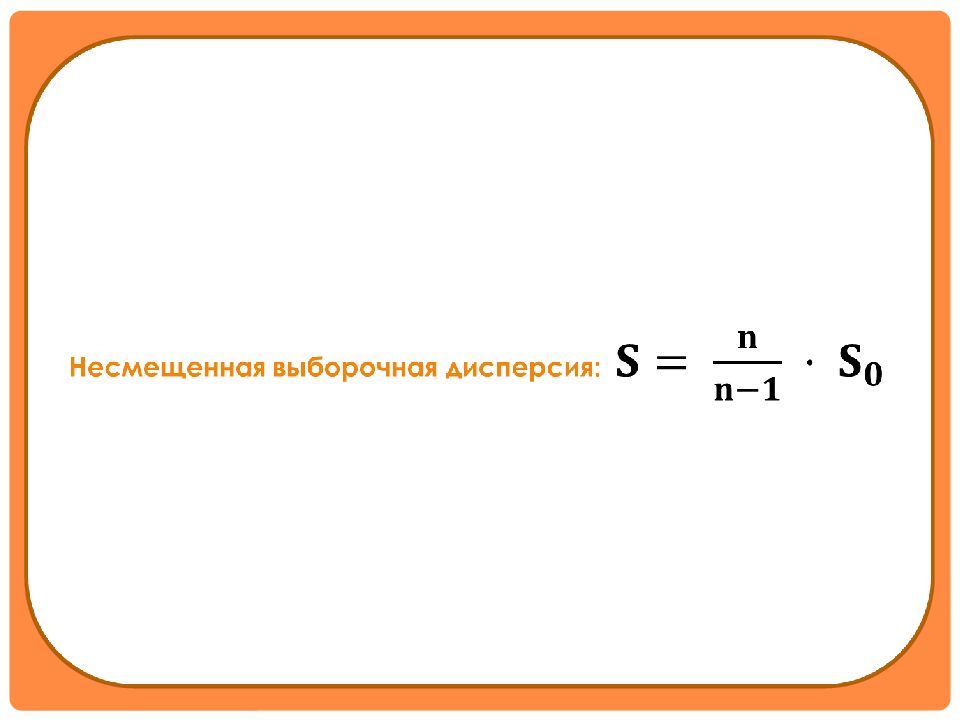
Выборочной дисперсией называют среднее арифметическое квадратов отклонений значений выборки от выборочного среднего: = Если выборка задана статистическим рядом, то =
Несмещенная выборочная дисперсия: :
Пример. Дана выборка 1,2,3,4,5. Найти выборочное среднее х, выборочную дисперсию, несмещенную выборочную дисперсию. Объем выборки n =5 = =
1. В результате 10 одинаковых проб были получены следующие значения содержания марганца: 0,69%; 0,70%; 0,67%; 0,66%; 0,697%; 0,67%; 0,68%; 0,67%; 0,68%; 0,68%. Вычислить выборочное среднее, выборочную дисперсию и несмещенную выборочную дисперсию. 2. При определении микроаналитическим способом содержания 230-та в данной пробе были получены следующие результаты: 9,29%; 9,38; 9,35; 9,43; 9,53; 9,48; 9,61; 9,68%. Вычислить выборочное среднее, выборочную дисперсию и несмещенную выборочную дисперсию. 3. В результате измерений диаметра капилляра в стенке легочных альвеол были получены следующие результаты: 2,83 мкм; 2,81; 2,85; 2,87; 2,86; 2,83; 2,85; 2,83; 2,84 мкм. Вычислить выборочное среднее, выборочную дисперсию и несмещенную выборочную дисперсию.
4. В результате измерений были получены следующие результаты: 3,2; 3,4; 3,3; 3,5; 3,6; 3,7; 3,4; 3,3; 3,4; 3,7; 3,2. Вычислить выборочное среднее, выборочную дисперсию и несмещенную выборочную дисперсию. 5. При подсчете количества листьев у одного из лекарственных растений были получены следующие данные: 8,10,7,9,11,6,9,8,10,7. Вычислить выборочное среднее, выборочную дисперсию и несмещенную выборочную дисперсию. 6. Проведены измерения вязкости крови у 9 больных. Значения относительной вязкости крови у больных составили: 5, 4, 3, 2, 6, 3, 4, 8, 10. Найти несмещенные оценки генеральной средней вязкости крови и генеральной дисперсии.
САНИТАРНАЯ (МЕДИЦИНСКАЯ) СТАТИСТИКА Санитарная (медицинская) статистика является одной из основных отраслей статистической науки и важнейшим методическим разделом социальной гигиены и организации здравоохранения. В задачи санитарной статистики входит: 1) определение уровня и сдвигов в здоровье отдельных групп населения; 2) оценка влияния социально-биологических факторов на здоровье населения; 3) анализ данных о сети, кадрах, деятельности лечебно-профилактических учреждений (ЛПУ); 4) определение эффективности лечебно-профилактических мероприятий; 5) использование статистических методов в экспериментальных, клинико-биологических, социально-гигиенических исследованиях.
Статистическая совокупность, ее элементы, признаки Статистическая совокупность - группа, состоящая из множества относительно однородных элементов (единиц наблюдения). (Например, группа оперированных, население на участке, больные стационара, новорожденные на данном участке, пациенты поликлиники, больные на дому и т.п.) Единица наблюдения - каждое отдельное явление, подлежащее учету, наделенное признаками сходства.
Понятие о медико-демографических показателях, расчет общих показателей рождаемости, смертности Основными медико-демографическими показателями являются рождаемость, смертность, естественный прирост населения и др. Коэффициентом (или показателем) рождаемости называется число родившихся за год, приходящееся на 1000 населения : ·1000 Коэффициентом общей смертности служит количество умерших за год на 1000 населения: Естественный прирост населения можно установить лишь при одновременном изучении рождаемости и смертности в их взаимной связи. Показатель естественного прироста определяется путем вычисления разности между показателями рождаемости и смертности населения.
Показатели, определяющие деятельность работы поликлиники Соблюдение принципа участковости в работе участковых врачей в поликлинике : Удельный вес посещений, сделанных сельскими жителями :
Среднегодовая занятость койки: Показатель средней длительности пребывания больного на койке: Оборот койки: Показатель больничной летальности:
Пример. Определите качественные показатели деятельности поликлиники N° 2 города В, обслуживающей 50 тыс. населения. В отчете за 1995 г. указано, что жителями за год к терапевтам сделано 130000 посещений, из них к своим участковым врачам - 90 000. Оказана медицинская помощь 8000 жителям сельских пригородов (приписных к больнице). Проведен целевой осмотр для выявления туберкулеза - 2500 человек. Из 300 зарегистрированных больных взято на диспансерное наблюдение 150 (больных язвенной болезнью желудка и двенадцатиперстной кишки.
Соблюдение принципа участковости в работе участковых врачей в поликлинике: = = Вывод. Участковость в поликлинике организована недостаточно (чем выше процент участковости, тем правильнее организована работа поликлиники. Хорошим показателем надо считать 80-85% и более).
Удельный вес посещений, сделанных сельскими жителями: = = Этот показатель не должен быть больше 7%, он свидетельствует об объеме лечебной помощи, получаемой сельскими жителями в городских больницах.
Охват населения целевыми осмотрами для выявления туберкулеза: = Полученный показатель довольно низкий. Охват диспансерным наблюдением (язвенная болезнь): = =
Объем работы стационара определяется обычно в так называемых койко-днях. Число проведенных больными койко-дней за год подсчитывается путем суммирования числа больных, числящихся на 8 ч утра каждого дня. Например, 1 января в больнице было 150 больных, 2 января - 160, а 3 января - 128. За эти 3 дня проведено койко-дней: 150+160+128 =438. Исходя из количества фактически проведенных койко-дней, определяют среднегодовую занятость койки или показатель использования койки, или среднее число дней работы койки в году. Например, 4088 больными (из них 143 умерших) проведено 65410 койко-дней, число среднегодовых развернутых коек было 190: = Работа койки в городских больницах менее 340 дней в году указывает на плохую, недостаточно оперативную работу больницы. Для сельских участковых больниц и родильных отделений принята более низкая норма: 310-320 дней.
С редней длительности пребывания больного на койке : = Один больной в среднем провел в стационаре 16 дней. Оборот койки вычисляется по следующей формуле: = На каждой койке в течение года лежал 21 больной. Этими показателями определяется эффективность использования койки.
Эффективность лечения характеризует показатель больничной летальности : =
Деятельность работы ФАП характеризуется следующими показателями 1. Число посещений ФАП на 1 жителя в год: 2. Нагрузка фельдшера на приеме в час:
3. Нагрузка фельдшера в день: 4. Нагрузка фельдшера на дому в день: 5. Удельный вес посещений на дому:
6. Удельный вес заболеваний ангиной: 7. Удельный вес заболеваний гипертонической болезнью: 8. Среднее число патронажных посещений на дому к детям в возрасте до 3 лет:
Задача. Определите показатели нагрузки фельдшера и деятельности ФАП села Покровского. В 1992г. Число жителей составляло 500 человек, детей до 3 лет – 70. фельдшер ведет прием 3часа в день. Число посещений к фельдшеру составило 2200, число посещений на дому составило 500. Выявлено 600 заболеваний, из них 24 случая заболеваний ангиной, 12 случаев гипертонической болезни. Число патронажных посещений на дому к детям до 3 лет составило 420.
1. Число посещений на 1 жителя в год: = 2. Нагрузка фельдшера на приеме в час: = =
3. Нагрузка фельдшера в день: = 4. Нагрузка фельдшера на дому в день: =
5. Удельный вес посещений на дому: 6. Удельный вес заболеваний ангиной:
7. Удельный вес заболеваний гипертонической болезнью: 8. Среднее число патронажных посещений на дому к детям в возрасте до 3 лет :
