Первый слайд презентации: Энергетический метод расчёта упругих систем
1 Энергетический метод расчёта упругих систем
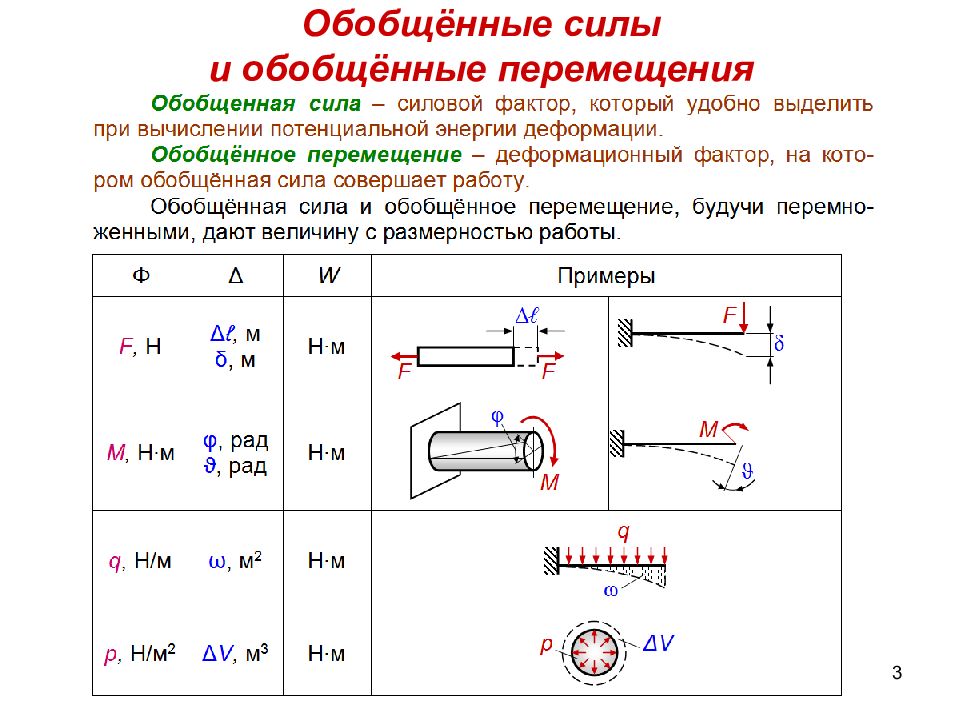
Слайд 3: Обобщённые силы и обобщённые перемещения
3 Обобщённые силы и обобщённые перемещения
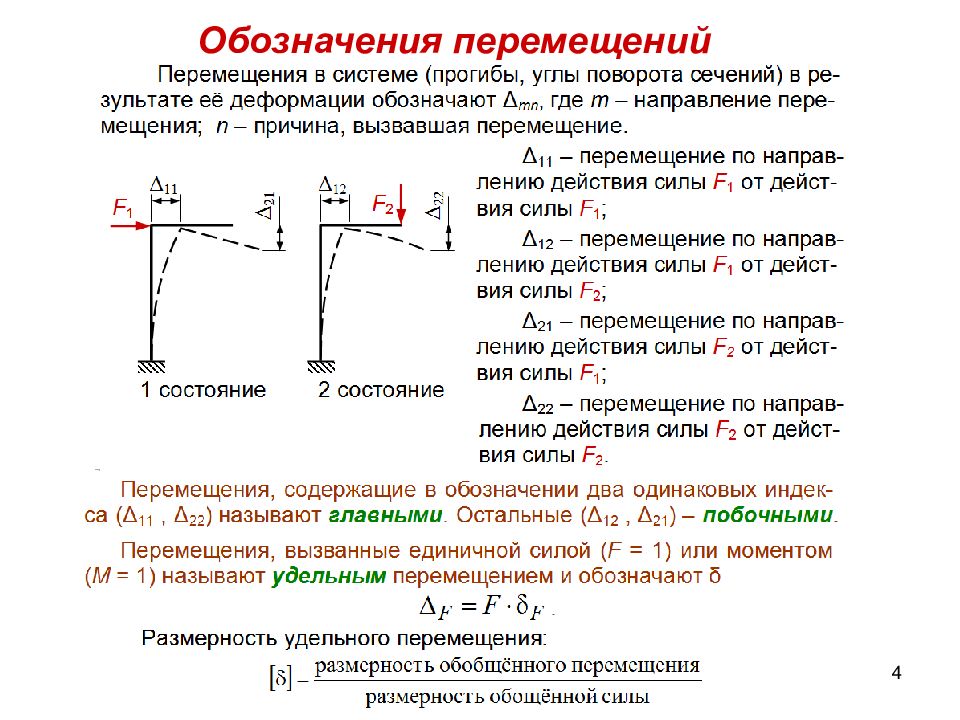
Слайд 5
5 Теорема о взаимности работ (теорема Бетти) Рассмотрены два варианта последовательности нагружения системы:
Слайд 6
6 Энри́ко Бе́тти ( итал. Enrico Betti, 1823 – 1892 ) — итальянский математик и физик. Известен своими пионерскими работами по топологии, занимался также абстрактной алгеброй и математическим анализом. Внёс вклад в многомерную теорию связности поверхностей, в теорию потенциала. В физике исследовал проблемы распространения тепла, гидродинамики, теории капиллярности. В теории упругости открыл важную теорему Бетти. С 1862 года – член итальянского парламента, в 1884 году стал сенатором.
Слайд 7
7 Теорема о взаимности перемещений (теорема Максвелла) Джеймс Клерк Ма́ксвелл ( англ. James Clerk Maxwell; 1831-1879) – британский фи-зик и математик. Член Лондонского королевского общества (1861). Максвелл за-ложил основы современной классической электродинамики ( уравнения Максвелла ), ввёл в физику понятия тока смещения и электромагнитного поля, получил ряд следствий из своей теории (предсказание электромагнитных волн, электромаг-нитная природа света, давление света и другие). Один из основателей кинети-ческой теории газов (установил распределение молекул газа по скоростям). Од-ним из первых ввёл в физику статистические представления, показал статис-тическую природу второго начала термодинамики (« демон Максвелла »), получил ряд важных результатов в молекулярной физике и термодинамике (термодина-мические соотношения Максвелла, правило Максвелла для фазового перехода жидкость — газ и другие). Пионер количественной теории цветов; автор принци-па цветной фотографии. Среди других работ Максвелла — исследования по ус-тойчивости колец Сатурна, теории упругости, и механике ( фотоупругость, теорема Максвелла), оптике, математике.
Слайд 9
9 Христиан Отто Мор ( нем. Christian Otto Mohr ; 1835 - 1918 ) – немецкий инженер и учёный в области теоретической механики и сопротивления материалов. Учился в Высшей технической школе в Ганновере. C 1855 года работал над сооружением же-лезных дорог и мостов в Ганновере и Ольденбурге. С 1867 года профессор, сначала в Штутгарте, затем в Дрездене. Занимался проблемами сопротивления материалов. Вывел формулу для определения перемещений в стержневых системах в 1874 г. Предложил в 1882 г. графическое представление напряжённого состояния и на его основе в 1990 г. разработал критерий плас-тичности и разрушения.
Слайд 11
11 Верещагин Андрей Константинович (1896 — 1959) - физик. В 1918 г. он вступил в РКП (б) и в качестве политработника участвовал в гражданской войне. В 1921 г. А. К. Верещагин поступил в Московский институт инженеров транспорта. В 1924 г., будучи студентом, предложил правило для вычисления интеграла Максвелла - Мора для частного случая прямого стержня постоянного поперечного сечения. После окончания теоретического курса оставил институт и поступил на физико-математичес-кий факультет Московского университета, который окончил в 1930 г. Затем он работал в различных научно-исследовательских институтах и стал крупным специалистом в обла-сти минной электротехники. В 1937—1938 гг. преподавал в Военно-морской академии, а в 1947—1948 гг. — во Всесоюзном заочном энергетическом институте. Во время Вели-кой Отечественной войны Верещагин принимал активное участие в обороне Одессы и Севастополя. В 1956 г. инженер-полковник А. К. Верещагин по состоянию здоровья вышел в отставку. Способ Верещагина - графоаналитический способ определения перемещений
Слайд 12
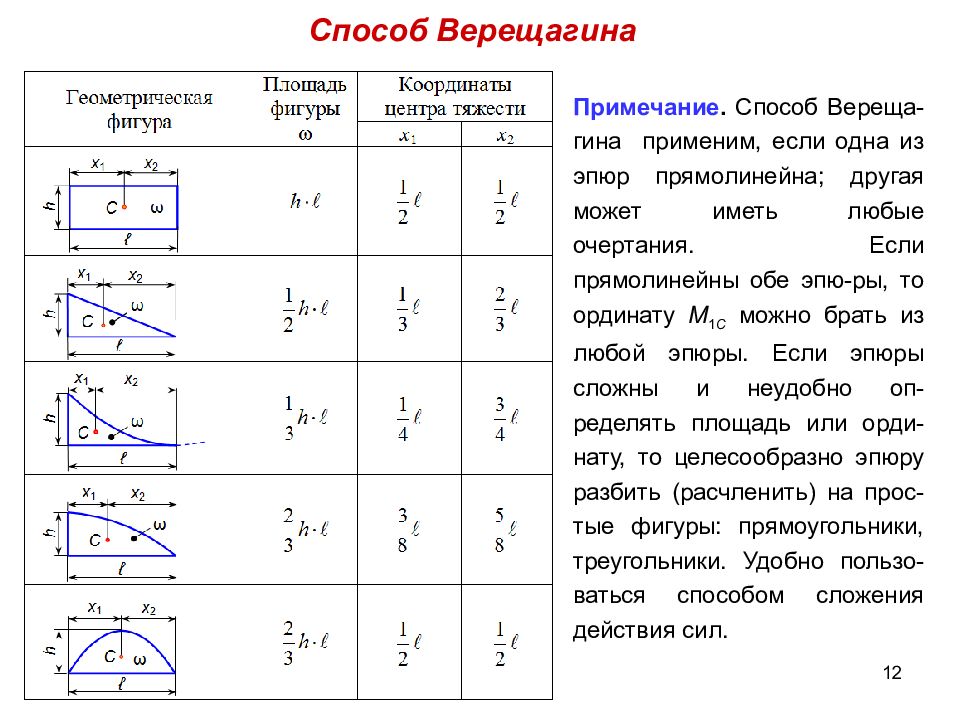
12 Примечание. Способ Вереща-гина применим, если одна из эпюр прямолинейна; другая может иметь любые очертания. Если прямолинейны обе эпю-ры, то ординату М 1 С можно брать из любой эпюры. Если эпюры сложны и неудобно оп-ределять площадь или орди-нату, то целесообразно эпюру разбить (расчленить) на прос-тые фигуры: прямоугольники, треугольники. Удобно пользо-ваться способом сложения действия сил. Способ Верещагина
Слайд 16
16 Ферма – несущая конструкция, состоящая из прямолинейных стержней, узло- вые соединения которых при расчёте условно принимаются шарнирными. Фермы применяют главным образом в строительстве (покрытия зданий, пролёт- ные строения мостов, мачты, опоры линий электропередачи, гидротехнические затворы и др.), а также в качестве несущих конструкций машин и механизмов.
Слайд 17
17 Рама – стержневая система, элементы которой (стойки, ригели, подкосы) во всех или в некоторых узлах жестко соединены между собой. Рамы служат в основном несущими конструкциями зданий, мостов, эста- кад и др. сооружений, а также рабочих и транспортных машин.
Слайд 18
18 ВОЗДУШНЫЕ ГИМНАСТЫ НА ТРАПЕЦИЯХ Различают рамы пространственные и плоские Плоская система – система конструкций, в которой оси симметрии всех элементов и линии действия внешних сил находятся в одной плоскости.