УРАВНЕНИЯ МАКСВЕЛЛА
Джеймс Клерк Максвелл (1831-1879) Гипотеза Максвелла о вихревом электрическом поле. 1-ое уравнение Максвелла. При электромагнитной индукции в замкнутом проводящем контуре возникает ЭДС индукции ε i Следовательно, имеются сторонние силы ( силы не кулоновской природы ) Какова природа этих сторонних сил ? Движущийся проводник Роль сторонней силы – составляющая силы Лоренца 2. Конфигурация контура не изменяется (проводник неподвижен), магнитный поток через поверхность, ограниченную контуром, меняется за счёт изменения магнитного поля: само- и взаимная индукция, движение магнита. 1. Какая сторонняя сила создаёт ЭДС в этом случае??
Гипотеза Максвелла о вихревом электрическом поле. 1-ое уравнение Максвелла. 2. М агнитный поток через поверхность, ограниченную контуром, меняется за счёт изменения магнитного поля. Какая сторонняя сила создаёт ЭДС в этом случае ε i ?? Максвелл: изменяющееся во времени магнитное поле приводит к возникновению вихревого (не потенциального) электрического поля, существование которого не зависит от наличия проводников напряженность вихревого электрического поля в точке : – сила, действующая со стороны вихревого электрического поля на точечный заряд q, помещенный в данную точку. - сторонняя сила по аналогии с определением напряженности электростатического поля В проводнике, помещенном в вихревое электрическое поле, возникает индукционный ток - движение свободных носителей заряда под действием сил вихревого электрического поля.
Гипотеза Максвелла о вихревом электрическом поле. 1-ое уравнение Максвелла. Максвелл: контур ℓ – не обязательно проводящий! Это может быть воображаемый, мысленный контур. П еременное магнитное поле приводит к появлению вихревого электрического поля независимо от того, в какой среде это происходит. Например, если магнитное поле меняется в вакууме, то вихревое электрическое поле существует в вакууме (как и кулоновское)
Гипотеза Максвелла о вихревом электрическом поле. 1-ое уравнение Максвелла. = 0 ≠ 0 ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ПОТЕНЦИАЛЬНОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ Особенности вихревого электрического поля Источником вихрев. электр. поля не являются электр. заряды = 0 Нельзя ввести потенциал ВСЕГДА: Источником потенц. электр. поля являются электр. заряды ≠ 0 Теорема Гаусса Поле характеризуется потенциалом Силовые линии вихревого электр. п оля замкнуты (не имеют начала и конца) Силовые линии потенц. электр. поля начинаются и заканчиваются на электрических зарядах
1-ое уравнение Максвелла + проекция напряженности результирующего электрического поля на направление элементарного перемещения вдоль замкнутого контура 1-ое уравнение Максвелла + 3 -е уравнение Максвелла
2-е ур -е Максвелла
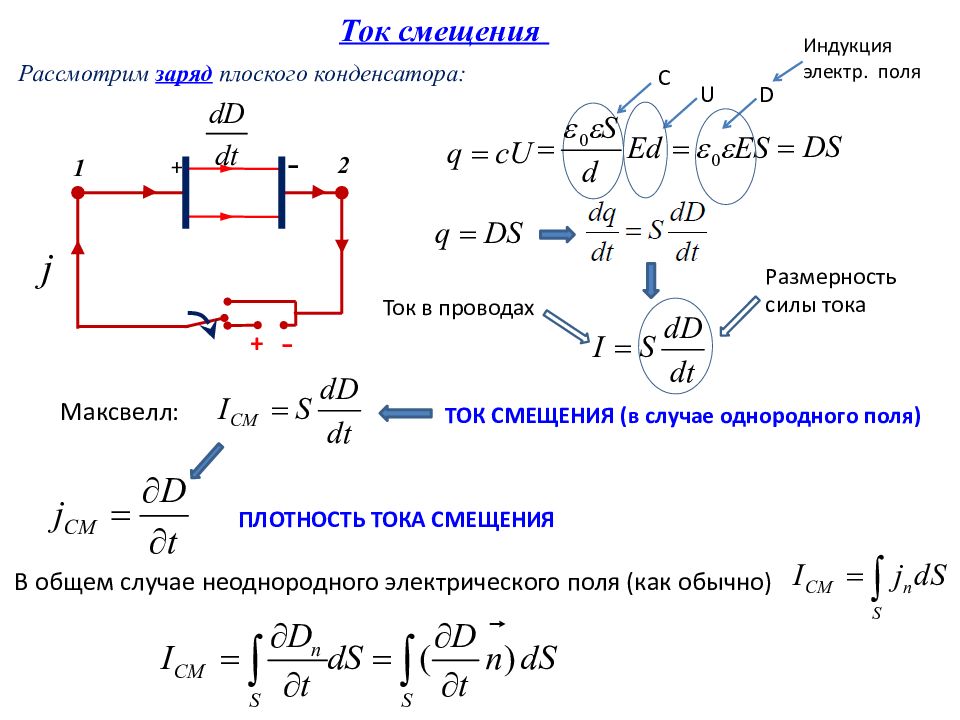
Ток смещения Рассмотрим заряд плоского конденсатора: - + + - 1 2 Ток в проводах Размерность силы тока Максвелл: ТОК СМЕЩЕНИЯ (в случае однородного поля) ПЛОТНОСТЬ ТОКА СМЕЩЕНИЯ В общем случае неоднородного электрического поля (как обычно) С U D Индукция э лектр. поля
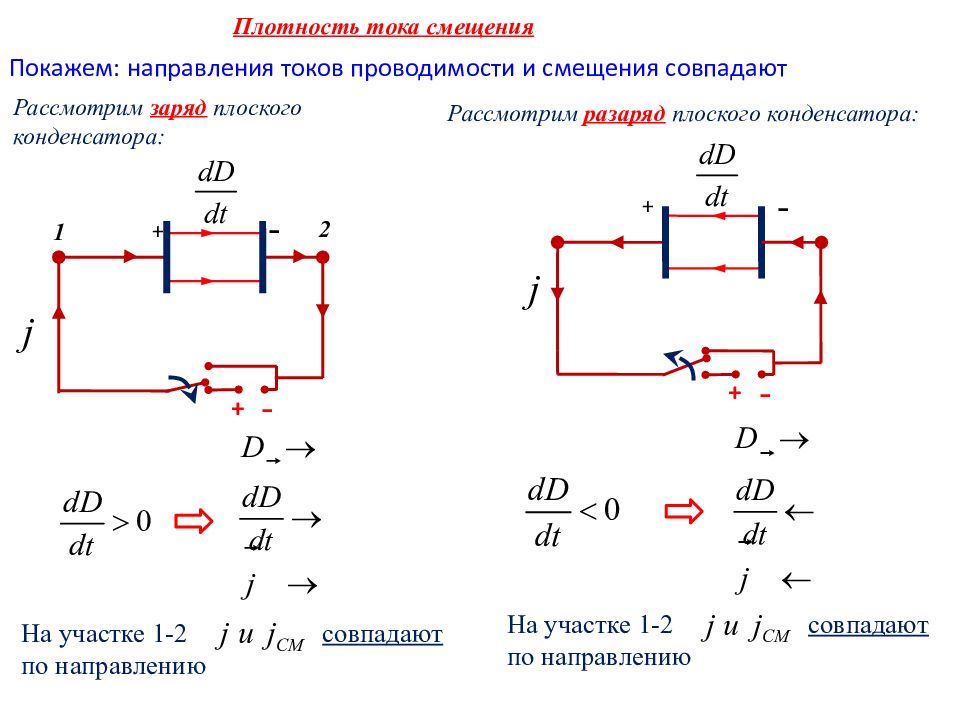
Плотность тока смещения Рассмотрим заряд плоского конденсатора: - + + - 1 2 Покажем: направления токов проводимости и смещения совпадают На участке 1-2 совпадают по направлению Рассмотрим разаряд плоского конденсатора: + - + - На участке 1-2 совпадают по направлению
Н а границе пластин конденсатора и диэлектрика плотность тока проводимости и плотность тока смещения совпадают не только по направлению, но и по величине. - + + - 1 2 Действительно: В плоском конденсаторе Ток в проводах Ток смещения Поле однородно Таким образом, линии тока проводимости в проводах на границах обкладок непрерывно переходят в линии тока смещения внутри конденсатора (независимо от того заряжается или разряжается конденсатор).
Ток смещения создает в пространстве его окружающем магнитное поле такое же, как и магнитное поле эквивалентного тока проводимости. Гипотеза Максвелла
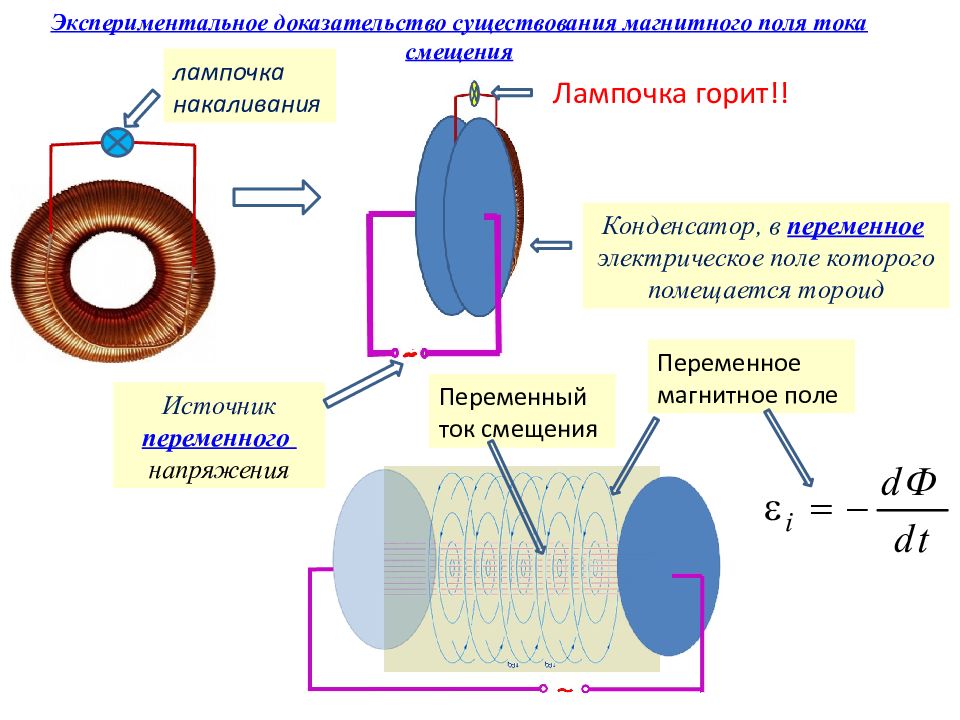
лампочка накаливания Экспериментальное доказательство существования магнитного поля тока смещения Переменный ток смещения Переменное магнитное поле Конденсатор, в переменное электрическое поле которого помещается тороид Источник переменного напряжения Лампочка горит!!
Теорема о циркуляции вектора магнитной индукции: Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов ( полному току ), охватываемых этим контуром, умноженной на ……. МАКСВЕЛЛ: полный ток Постоянный ток Плотность полного тока Равноценны в отношении создания магнитного поля Плотность тока проводимости Плотность тока смещения Из всех свойств, присущих току присуще лишь одно – создавать в окружающем пространстве магнитное поле
Рассмотрим проводящую среду, в которой существуют переменное электрическое поле и ток проводимости. 2-е уравнение Максвелла Теорема о циркуляции вектора магнитной индукции: проводящая среда п роизвольный контур 2-ое уравнение Максвелла
п роизвольный контур 2-ое уравнение Максвелла 2-ое уравнение Максвелла справедливо для любой среды, в том числе для диэлектрика, вакуума или неоднородной среды, включающей в себя проводники и диэлектрики. Например, в случае вакуума (воздуха)
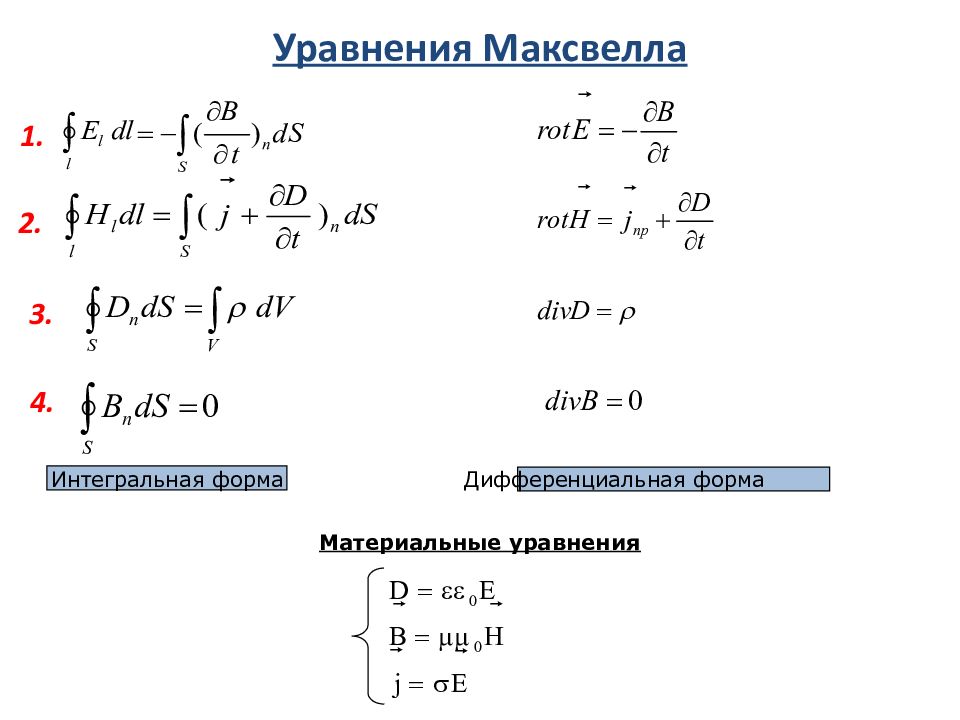
2. 3. 4. Система уравнений Максвелла в интегральной форме 1. циркуляция вектора напряженности электрического поля по произвольному контуру, равна «минус » скорости изменения магнитного потока через поверхность, ограниченную этим контуром ( закон ЭМИ Фарадея ). циркуляция вектора напряжённости магнитного поля по произвольному контуру равна алгебраической сумме токов проводимости и токов смещения, охватываемых этим контуром ( теорема о циркуляции для м.п. +.ток смещения ) поток вектора электрической индукции через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности ( теорема Гаусса – закон Кулона) ). Поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю (отсутствие магнитных зарядов) Дополнив основные факты из области электромагнетизма установлением магнитных действий токов смещения, Максвелл написал систему фундаментальных уравнений электродинамики.
Система уравнений Максвелла в интегральной форме 1. 2. 3. 4. Уравнения Максвелла - это основные аксиомы электродинамики полученные путём обобщения опытных фактов (их нельзя вывести). Из уравнений Максвелла следует возможность существования электромагнитных волн.
Система уравнений Максвелла в интегральной форме 1. 2. 3. 4. 4 уравнения Максвелла не составляют полной системы уравнений электромагнитного поля. У равнения Максвелла не содержат данных о свойствах среды. У равнения Максвелла следует дополнить соотношениями, характеризующими свойства среды – «материальными уравнениями» Если электромагнитное поле н е слишком сильное, н е меняется слишком быстро в о времени и резко в пространстве, о тсутствуют ферромагнетики и сегнетоэлектрики, м атериальные уравнения
Сивухин
Уравнения Максвелла в дифференциальной форме
Математическое введение к ур-ниям Максвелла в дифференциальной форме Теоремы Стокса и Остроградского-Гаусса Т. Стокса Т. Остроградского - Гаусса где Дивергенция векторного поля, скаляр Ротор векторного поля, вектор S – поверхность ограниченная контуром l V – объём внутри замкнутой поверхности S
Пример перехода к дифф. форме. Теор. Гаусса (3-е ур -е М.) Закон Фарадея (1-е ур -е Максвелла ) = Т. О.– Г. = Т. Стокса Физ. смысл дивергенции вектора ρ = 0, поток через замкн. поверхность =0, нет источников и стоков, поток не расходится. При этом дивергенция характеристика расходимости потока
Уравнения Максвелла Интегральная форма Дифференциальная форма Материальные уравнения 1. 2. 3. 4.
