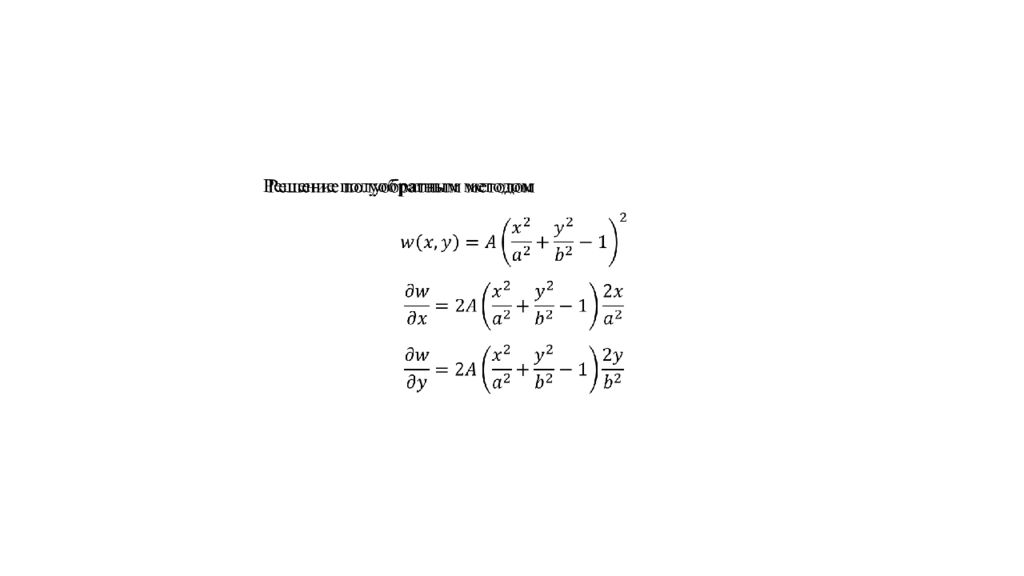Слайд 2
Теория же упругости – это наука, которая занимается вопросами определения напряженно-деформированного состояния упругих тел произвольной конфигурации. Теория упругости основывается на предположении об идеальной упругости тела и законе Гука. Методы теории упругости позволяют: 1. оценить точность приближенных решений сопротивления материалов и установить предел применимости этих решений, 2. решать задачи для произвольных форм исследуемых тел.
Слайд 3
Основные гипотезы теории упругости. 1. Гипотеза о сплошности строения тела. Тело непрерывное до деформации остается непрерывным и после деформации. 2. Гипотеза о естественном ненапряженном состоянии тела. Напряжения в теле считаются нулевыми до приложения нагрузки. 3. Гипотеза об идеальной упругости. Все тела считаем идеально упругими, а процесс деформирования обратимым. 4. Гипотеза о шаровой изотропии. Физико – механические свойства материалов по всем направлениям одинаковы. 5. Гипотеза об однородности. Механические свойства материалов во всех точках тела одинаковы. 6. Принцип «автономной» прочности. Напряженное состояние в данной точке тела зависит от состояния деформации в этой же точке. 7. Принцип Сен-Венана. Если в какой –то малой части тела приложена уравновешенная система сил, то она вызывает напряжения в теле, которые убывают по мере удаления от этой части тела. 8. Гипотеза о малости перемещений. Перемещения точек тела, вызванные ее деформацией, малы по сравнению с размерами тела.
Слайд 4
Усилия и напряжения Усилия: Поверхностные (распределены по поверхности) и объемные (действуют во всех точках сооружения-силы инерционные, собственный вес и т.д.) 2. Постоянные и переменные 3. Статические и динамические. 4. Внутренние и внешние. Напряжения: средние и истинные Деформации: относительные, линейные и сдвиговые.
Слайд 5
Равновесие параллелепипеда Дифференциальные уравнения равновесия элементарного параллелепипеда. Закон парности касательных напряжений (1) Совокупность напряжений на гранях параллелепипеда образует тензор напряжений
Слайд 6
Уравнение Навье Σ X =0 Получим уравнения Навье или дифференциальные уравнения равновесия (2).
Слайд 7
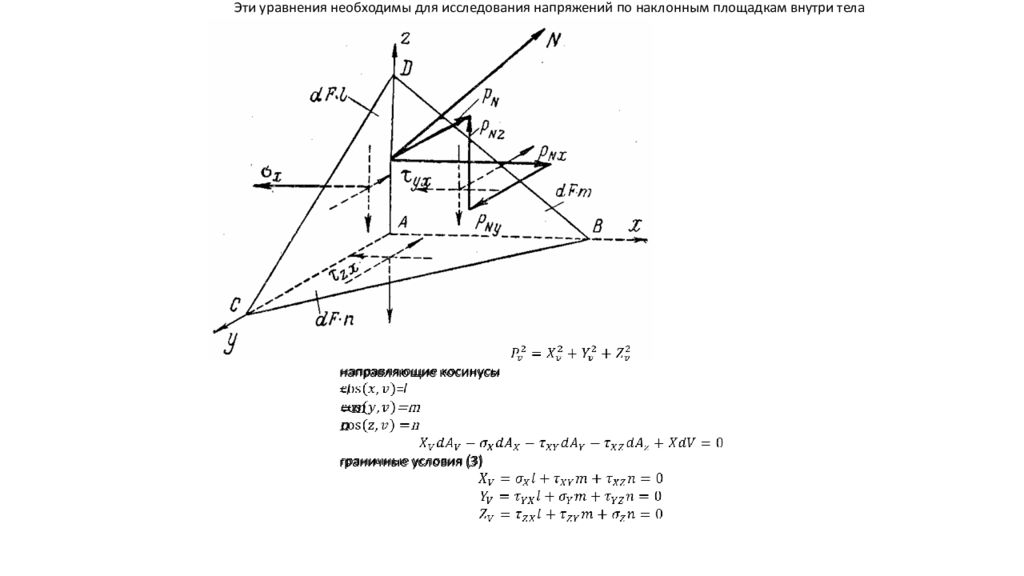
Уравнения равновесия тетраэдра. Эти уравнения необходимы для исследования напряжений по наклонным площадкам внутри тела и для записи граничных условий на поверхности тела. направляющие косинусы = l =m n граничные условия (3)
Слайд 8
Инварианты напряжений Формулы преобразования напряжений для наклонной площадки. n=0 l 2 + m 2 + n 2 =1
Слайд 9
Главные напряжения Корни данного уравнения не зависят от выбора координатной системы и должны сохранять постоянные значения при преобразовании осей, т.е. они являются инвариантами. Инварианты выражают через главные напряжения, приравняв касательные напряжения нулю. И корнями уравнений будут главные напряжения σ 1, σ 2, σ 3
Слайд 10
Шаровой тензор напряжений и тензор девиатор Разрушение происходит от изменения обьема и формы. Тензор напряжений Шаровой тензор выделяет из напряженного состояния равномерное всестороннее растяжение или сжатие, при котором изменяется только обьем данного тела без изменения формы. Тензор девиатор характеризует состояние сдвига, при котором изменяется форма элемента без изменения объема.
Слайд 11
Инварианты деформаций Уравнения деформаций по наклонной площадке. Линейный инвариант Квадратичный инвариант
Слайд 13
Шаровой тензор деформаций и тензор девиатор Шаровой тензор деформаций тензор девиатор деформаций
Слайд 14
Компоненты деформаций Условие совместности деформаций. 6 компонент деформации в каждой точке определяются функциями u, v, w, которые являются функциями перемещения. Увеличение ребра параллелепипеда по оси Х, т.е. его абсолютное удлинение вызванное деформацией, равно. Линейная деформация (относительное удлинение) в направлении Х представляет отношение абсолютного удлинения ребра к его исходной длине dx
Слайд 15
Рассмотрим изменение угла между двумя ребрами. Точка Р получила перемещения u, v в направлении осей х,у в точку P. Перемещение точки А в направлении у будет перемещение точки В в направлении х будет В итоге ребро РА получает малый угол α, а ребро РВ угол β. Угол АРВ уменьшился. Это и есть угловая деформация (относительный сдвиг)
Слайд 16
Уравнения Коши Таким образом мы запишем уравнения Коши (4). Геометрические уравнения Коши устанавливают зависимости между перемещениями и деформациями. Функции u, v. w будем считать заданными, и через них выразим деформации
Слайд 18
Уравнения Сен- Венана Условия совместности деформаций или уравнения Сен – Венана (5).
Слайд 19
Зависимость между напряжениями и деформациями. Деформационное состояние определяется шестью компонентами деформаций Перемещения точек определяются тремя компонентами перемещений Напряженное состояние определяется шестью компонентами напряжений
Слайд 20
Теория напряженного состояния дает 3 дифференциальных уравнения равновесия (2) Из теории деформаций имеем 6 уравнений Коши (4)
Слайд 21
Закон Гука. Рассмотрим уравнения закона Гука (6). Эти зависимости выражают закон Гука для случая изотропного материала. Связь между деформациями и напряжениями является линейной и полностью определяется двумя постоянными Е и μ, которые называются упругими постоянными.
Слайд 22
Рассмотрим функциональную зависимость между напряжениями и деформациями. σ x = f (ɛ x ; ɛ Y ; ɛ Z ; ꝩ xy ; ꝩ yz ; ꝩ zx ) или σ x = С 11 ɛ x + С 12 ɛ Y + С 13 ɛ Z + С 14 ꝩ xy + С 15 ꝩ yz + С 16 ꝩ zx ) σ y = С 21 ɛ x + С 22 ɛ Y + С 23 ɛ Z + С 24 ꝩ xy + С 25 ꝩ yz + С 26 ꝩ zx ) σ z = С 31 ɛ x + С 32 ɛ Y + С 33 ɛ Z + С 34 ꝩ xy + С 35 ꝩ yz + С 36 ꝩ zx ) = С 41 ɛ x + С 42 ɛ Y + С 43 ɛ Z + С 44 ꝩ xy + С 45 ꝩ yz + С 46 ꝩ zx ) = С 51 ɛ x + С 52 ɛ Y + С 53 ɛ Z + С 54 ꝩ xy + С 55 ꝩ yz + С 56 ꝩ zx ) = С 61 ɛ x + С 62 ɛ Y + С 63 ɛ Z + С 64 ꝩ xy + С 65 ꝩ yz + С 66 ꝩ zx ) В случае ортотропного материала соответствующие уравнения содержит 12 параметров: модули упругости в направлении координатных осей, Ex, Ey ; Ez модули сдвига Gxy, Gyz, G xz ; коэффициенты Пуассона, μ xy, μ yz. μ xz В общем случае анизотропии уравнение содержит 21 независимый параметр, а не 36, т.к. С ik = С ki.
Слайд 23
Девиаторная форма записи закона Гука. Соотношения упругости для изотропного материала содержат два физических параметра E и ν, либо G и λ.
Слайд 26
Основные уравнения теории упругости. Дифференциальные уравнения равновесия
Слайд 29
Эти 15 уравнений являются исходными в теории упругости, в них входят об ъ емные силы. Для поверхностных сил рассматриваем граничные условия (условия на поверхности)
Слайд 30
Прямая задача состоит в решении основных краевых задач теории упругости, т. е. в определении функций σij, εij и ui, характеризующих напряженно деформированное состояние тела в зависимости от внешнего воздействия на него. Обратная задача состоит в том, чтобы, задавшись либо перемещениями ui, либо компонентами тензора напряжений σij, определить из основных уравнений и соответствующих граничных условий все остальные функции, а также внешние силы, осуществляющие заданные перемещения или напряжения.
Слайд 31
Решение обратной задачи значительно проще, чем решение прямой задачи. Особо просто решается обратная задача, если задаться перемещениями ui. Дифференциальные зависимости Сен-Венана удовлетворяются тождественно. Решение выполняется в следующем порядке: на основании закона Гука определяются компоненты тензора напряжений, соответствующие принятым функциям ui, а из уравнений равновесия определяются внешние силы, при которых осуществляются заданные перемещения. Если задаваться компонентами тензора напряжений σij, то решение обратной задачи будет несколько сложнее. В этом случае перемещения находятся интегрированием соотношений Коши, что возможно, если компоненты тензора деформаций определяются из закона Гука по принятым функциям σij.
Слайд 32
Следовательно, компоненты тензора напряжений надо задавать так, чтобы выполнялись условия совместности, получающиеся из дифференциальных зависимостей Сен-Венана, путем исключения функций εij с помощью формул закона Гука (уравнения Бельтрами– Митчела ). Представим, что для определенной простой формы упругого тела при некоторых ограничениях его нагружения, задаваясь различными вариантами, например, функций σij, определили реализующие их внешние силы. Располагая набором таких решений обратной задачи, путем их комбинирования можно подобрать функции σij, которые будут соответствовать заданным конкретным нагрузкам, приложенным к рассматриваемому телу.
Слайд 33
Полуобратный метод Сен-Венана Решение прямой задачи в некоторых случаях можно эффективно получить с помощью так называемого полуобратного метода Сен-Венана. При решении конкретной задачи, например, в напряжениях, задаются из соображений физического характера задачи некоторые компоненты тензора напряжений и затем определяются остальные компоненты σij из уравнений равновесия при выполнении условий совместности Бельтрами– Митчела. Может случиться, что сделанные предположения о значениях некоторых компонент тензора напряжений будут противоречить или уравнениям равновесия, или условиям совместности. В этих случаях следует сделать иные предположения о значениях части компонент σij.
Слайд 34
Решение задач теории упругости в напряжениях Подставляя в уравнение совместности (5) вместо составляющих деформаций их выражения через напряжения, задаваемые формулами закона Гука (6), и используя дифференциальные уравнения равновесия (2), получим уравнения совместности деформаций, записанные через напряжения.
Слайд 36
Эти уравнения совместности называются уравнениями Бельтрами- Митчелла и справедливы, если обьемные силы отсутствуют или они постоянны. Для решения задачи необходимо рассмотреть дополнительно дифференциальные уравнения равновесия (2) и уравнения граничных условий (3). При интегрировании уравнений (8) произвольные функции, входящие в их общее решение, определяются из граничных условий (3). Затем по формулам закона Гука (6) можно найти деформации, а по формулам Коши (4) перемещения.
Слайд 37
Решение задач теории упругости в перемещениях. Решение задачи в перемещениях предусматривает введение в качестве неизвестных u ( x, y, z ), v ( x, y, z ), w ( x, y, z )
Слайд 38
Рассматривая уравнения закона Гука в девиаторной форме (7) и уравнения Коши (4) имеем (11)
Слайд 40
Подставляя полученные уравнения в дифференциальное уравнение равновесия (2) получим (12) ɛ v =ɛ x +ɛ y +ɛ z Эти уравнения называются уравнениями равновесия в перемещениях Ламе.
Слайд 41
Рассматривая уравнения закона Гука в девиаторной форме (7), уравнения Коши (4) и граничные условия (3) получим поверхностные условия (13) Уравнения Ламе (12) и уравнения с поверхностными условиями (13 ) определяют функции u, v, w.Затем по формулам Коши (4) можно найти деформации, а по формулам закона Гука в девиаторной форме (7) можно найти напряжения.
Слайд 42
Теорема о единственности решения. Теорема Кирхгоффа Решение статической задачи единственно, если выполняются условия 1.Тело односвязное 2.Начальные деформации и напряжения отсутствуют Заданы силы поверхностные X, Y. Z и обьемные для которых рассматриваются напряжения и соответственно.
Слайд 44
Для второго решения справедливы уравнения также условия совместности (5)
Слайд 45
Если первая система напряжений является решением, то она одновременно удовлетворяет всем уравнениям поверхностных условий (13). Если рассматриваем обе системы, то они обе удовлетворяют условиям (13). Путем вычитания их находим уравнения в которых отсутствуют внешние силы. Условия совместности (13) так же будут удовлетворяться соответствующими компонентами деформаций.
Слайд 46
Это распределение напряжений отвечает нулевым поверхностным и обьемным усилиям. Работа, совершаемая этими силами, равна нулю в процессе нагружения, т.е Но величина суммарной работы V 0 >0 для всех деформированных состояний. Интеграл от работы, совершенной силами, может обращаться в ноль при V 0 =0 во всех точках тела. Это требует, чтобы каждая из компонентов деформаций равнялась нулю. Следовательно, два компонента деформаций и два компонента напряжений тождественно совпадают, т.е. рассматриваемые уравнения имеют единственное решение.
Слайд 48
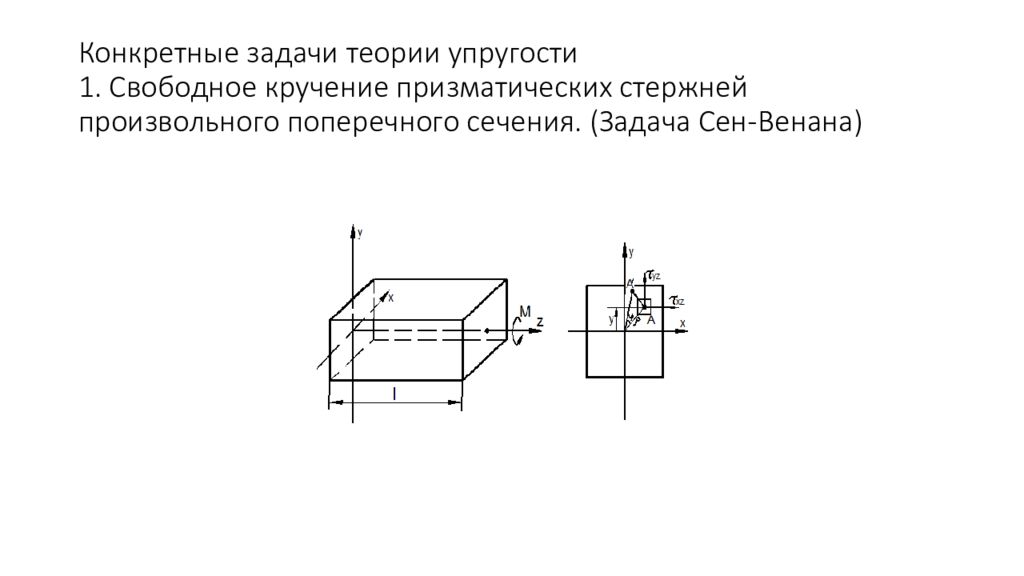
Решение проведем в перемещениях полуобратным методом Контур сечения поворачивается как жёсткое целое, а площадь сечения может исказиться. Пренебрегаем обьемными силами. θ- полный угол закручивания – погонный угол закручивания (1) w -функция депланации (искривление поперечного сечения) –функция депланации Сен-Венана.
Слайд 49
Определение напряжений и деформаций Формулы Коши О бобщенный закон Гука Касательные напряжения действуют в плоскости поперечного сечения.
Слайд 50
Уравнение Ламе Объёмные силы равны нулю, два уравнения тождественно нулевые, а первое примет вид (14): Таким образом, задача о кручении стержня сводится к решению гармонического уравнения (14). Предложенный метод решения называется полуобратным методом Сен-Венана, в котором часть искомых величин задаётся, а остальные неизвестные определяются из общих уравнений теории упругости при заданных статических граничных условий.
Слайд 52
Рассмотрим граничные условия и исключим нагрузки на боковые поверхности, т.е. l =0, и Yv =0 Zv =0, тогда φ – const φ ( S )=0 функция напряжений не зависит от контура. ((5) Крутящий момент (6)
Слайд 53
Проекция полного касательного напряжения, действующего в любой точке поперечного сечения на любое направление, лежащее в плоскости сечения, равна частной производной функции напряжения по нормали к этому направлению. (7)
Слайд 54
Решение задачи о свободном кручении стержней Решение задачи о свободном кручении стержней произвольной формы поперечного сечения сводится к отысканию функции двух переменных напряжений, связанных с касательными напряжениями, действующими в сечении, которые выражаются уравнениями (2) и (7). Функция φ должна удовлетворять уравнению (4).В случае односвязного сечения на контуре φ=0 (5).Функция φ связана с крутящим моментом и выражена в формуле (6), через которую можно определить.Перемещения определяются формулой (1). Причем входящая в нее функция перемещений Ψ является гармонической и может определяться через функцию напряжений φ уравнениями (3).
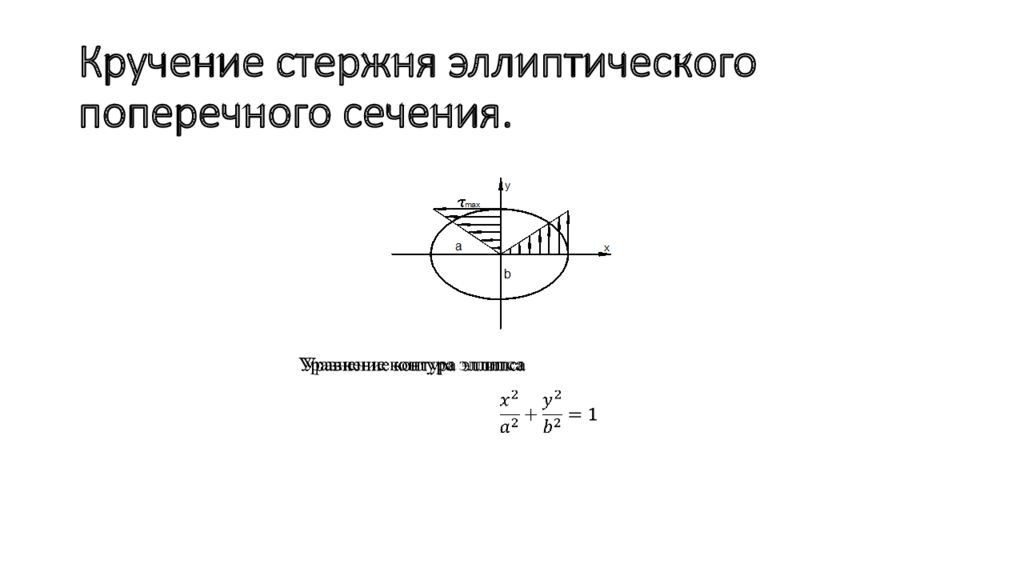
Уравнение контура эллипса
Слайд 57
Следовательно геометрическая характеристика жесткости эллиптического стержня По этой формуле рассчитываются геометрические характеристики любого многогранника
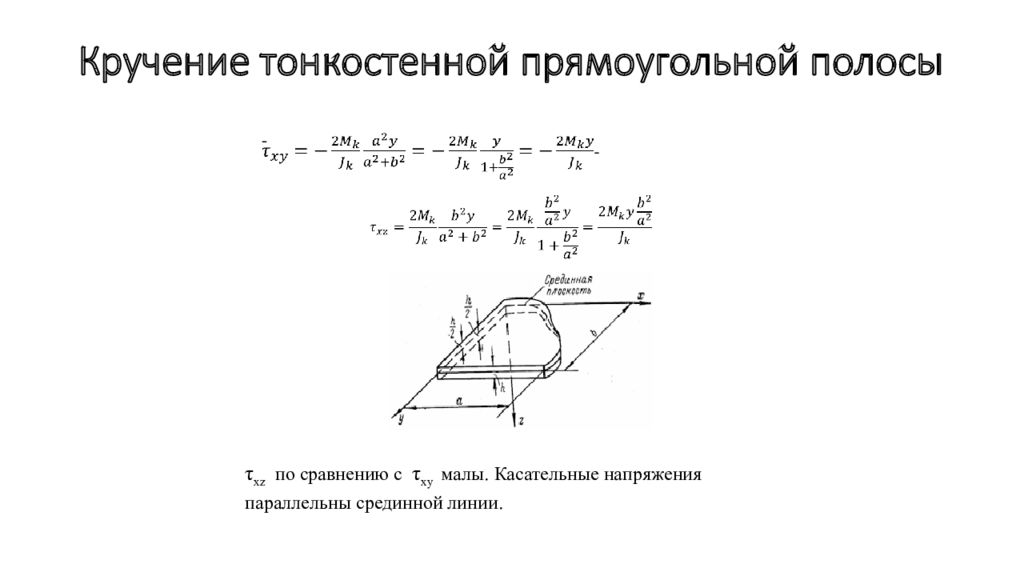
- τ xz по сравнению с τ xy малы. Касательные напряжения параллельны срединной линии.
Слайд 63
Тонкостенные стержни произвольного профиля где L длина всей срединной линии Для прокатных сталей
Слайд 64
Плоская задача теории упругости. В плоской задаче теории упругости рассматриваются плоское напряженное состояние и плоское деформированное состояние. Плоское деформированное состояние рассматривает призматические элементы конструкций при следующих условиях: w=0 или w= const ; z=0 ; z v =0 Перемещения формулы Коши
Слайд 67
Условия сплошности Сен-Венана Остальные три уравнения при расчете также тождественно равны нулю. В плоском деформированном состоянии неизвестными являются 8 функций: Напряжения σ x,σ y,τ xy, деформации ɛ x,ɛ y,γ xy, перемещения u, v. Для их нахождения есть два уравнения равновесия, три уравнения закона Гука и одно уравнение формулы Коши.
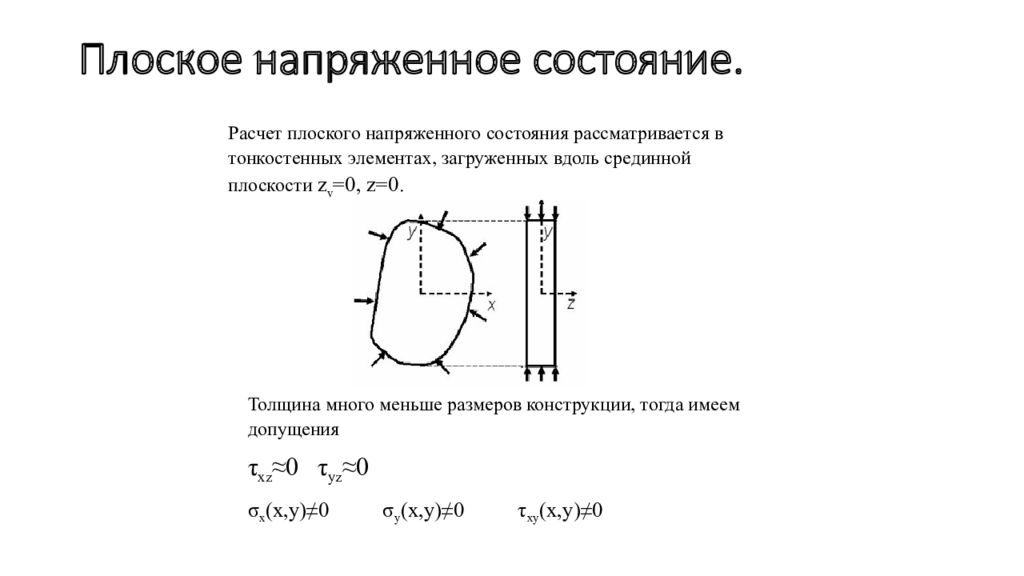
Слайд 68: Плоское напряженное состояние
Расчет плоского напряженного состояния рассматривается в тонкостенных элементах, загруженных вдоль срединной плоскости z v =0, z =0. Толщина много меньше размеров конструкции, тогда имеем допущения τ xz ≈0 τ yz ≈0 σ x ( x, y )≠0 σ y ( x, y )≠0 τ xy ( x, y )≠0
Слайд 71
Предполагается, что в уравнения Сен-Венана при приближенном расчете остается только одно уравнение Решение теории плоского напряженного состояния производится тем же аппаратом вычислений, что и для решения задач теории деформированного состояния. В этом случае первоначально надо найти напряжения. В качестве разрешающей системы уравнений выбирают 2 уравнения дифференциального равновесия равновесия и уравнение совместности деформаций. Причем последнее уравнение выражаем через напряжения.
Слайд 73
Заменим касательные напряжения на нормальные, используя дифференциальное уравнение равновесия. Суммируя их получим
Слайд 74
Получим Уравнение сплошности в напряжениях (уравнение Мориса-Леви) Решение плоской задачи в напряжениях:
Слайд 76
Изгиб пластинки. Деформации пластинки. Прогибы пластинки w не зависят от координаты z. Это означает, что все точки пластинки, лежащие на одной вертикали, получают одинаковые прогибы. Следовательно, достаточно определить прогибы срединной плоскости пластинки, чтобы знать прогибы всех ее точек. Производные перемещений u и v по координате z:
Слайд 77
Из гипотезы о нерастяжимости срединной линии следует Тогда Составляющие перемещения точек пластинки в направлениях осей х и у выражены через функцию прогибов срединной плоскости пластинки. Составляющие деформации в пластинке, отличные от нуля, найдем с помощью формул Коши, подставляя в них значения полученных составляющих перемещения. C оставляющие деформации выражены через одну функцию прогибов срединной плоскости пластинки.
Слайд 79
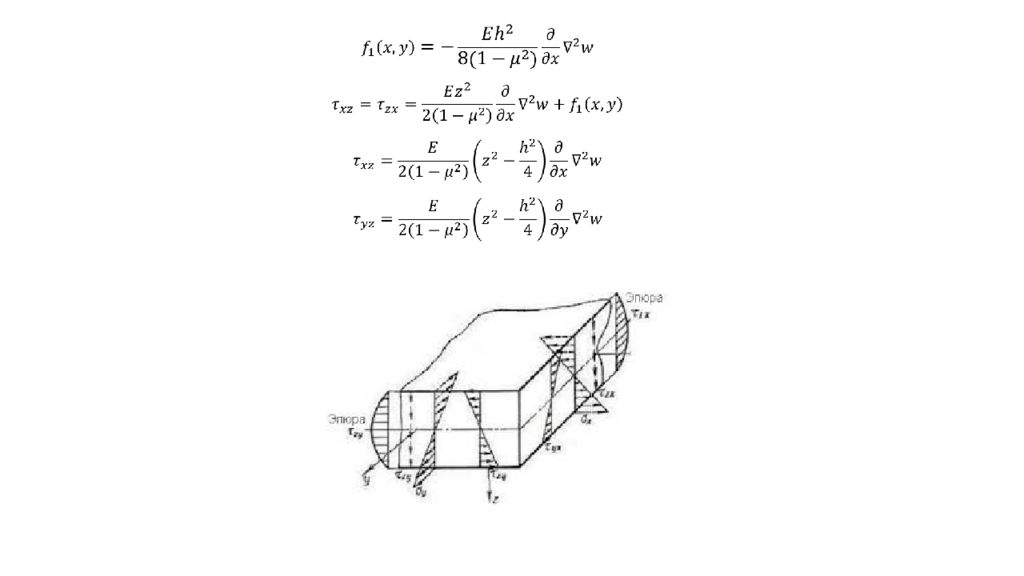
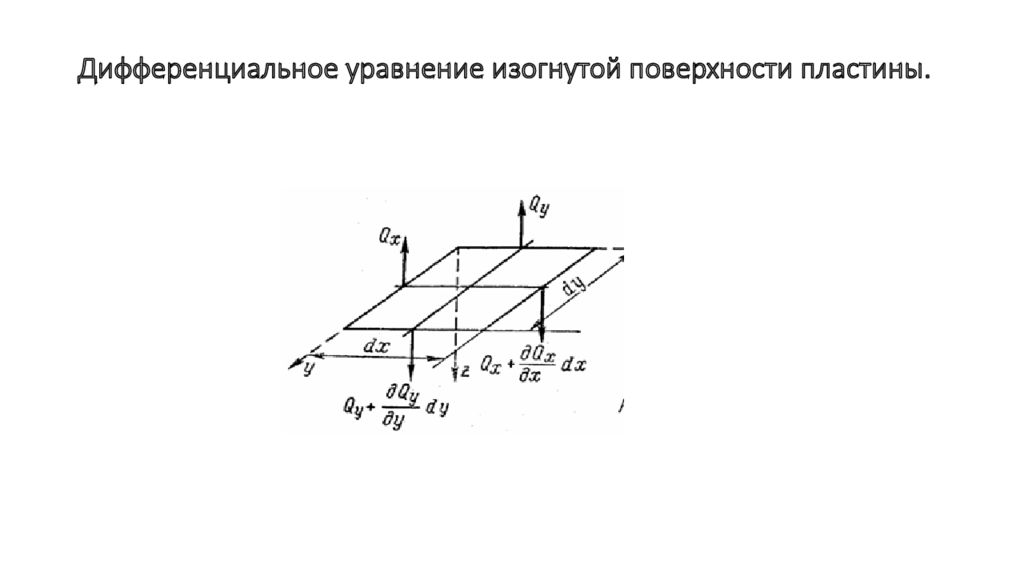
Решая совместно дифференциальные уравнения равновесия получим или Интегрируя по z получим При
Слайд 81
Усилия в пластинке Определение продольной силы Определение усилия сдвига В срединной плоскости нормальные и сдвиговые усилия равны нулю.
Слайд 82
Определение изгибающих моментов где D –цилиндрическая жесткость тонкой плиты.
Слайд 87
Граничные условия на краях пластины Шарнирно опертый край Для этого случая прогиб должен быть равен нулю. В то же время этот край может свободно поворачиваться относительно оси х; это значит, что изгибающие моменты М х обращаются на нем в нуль. M y =0, w =0 Тогда граничные условия имеют вид Так же обращается в нуль, поэтому уравнение можно считать эквивалентным уравнениям Соответственно для другой оси
Слайд 88
Жесткое закрепление Свободный край пластинки В этом случае принято, что по этому краю нет ни изгибающих или крутящих моментов, ни вертикальных перерезывающих сил M x =0, M k =0, Q xz =0
Слайд 89
Трех условий слишком много и для полного определения удовлетворяющих дифференциальному уравнению Софи Жермен прогибов достаточно двух условий. На этом основании объединенное требование относительно крутящего момента Мху и перерезывающей силы Q x для свободного края Граничные условия для свободно опертой пластинки принимают вид Условие, чтобы изгибающие моменты на свободном крае были равны нулю
Слайд 90: Расчет эллиптической в плане плиты
Уравнение эллипса Граничные условия 1. прогиб w =0 2. угол поворота