Слайд 2: Серия опытов
Серия опытов, приводящих к определению вероятности из геометрических соображений.
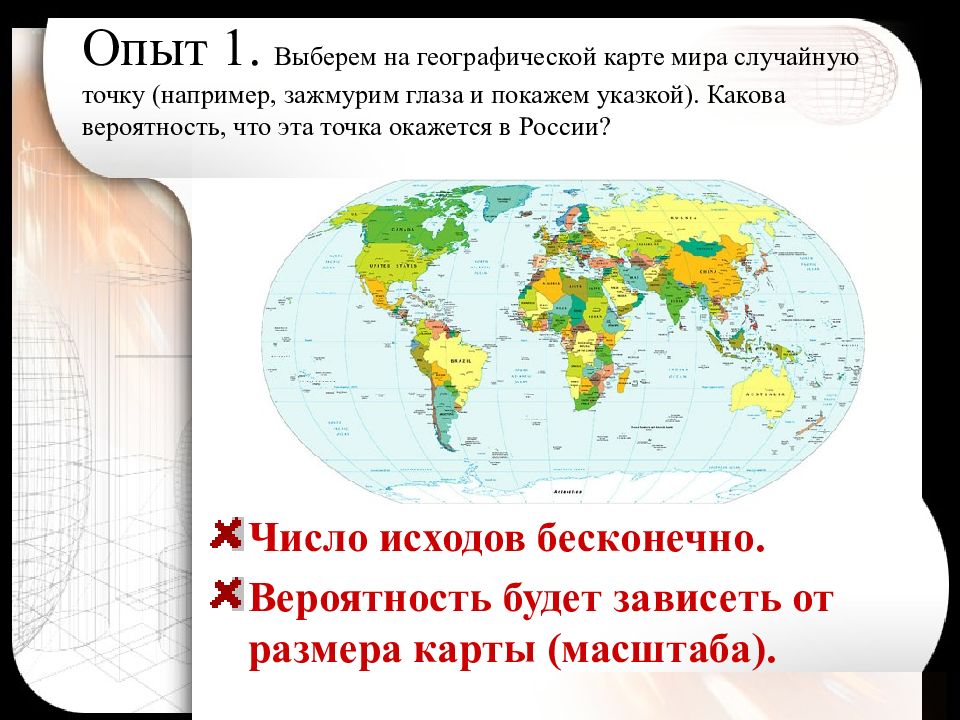
Число исходов бесконечно. Вероятность будет зависеть от размера карты (масштаба).
Очевидно, для ответа на вопрос нужно знать площадь всей карты и какую часть всей площади карты составляет Россия. Отношение этих площадей и даст искомую вероятность.
Слайд 5: Общий случай: в некоторой ограниченной области случайно выбирается точка. Какова вероятность, что точка попадет в область А ? На прямую L ?
А L
Слайд 6: Геометрическое определение вероятности
Если предположить, что попадание в любую точку области равновозможно, то вероятность попадания случайной точки в заданное множество А будет равна отношению площадей: Если А имеет нулевую площадь, то вероятность попадания в А равна нулю. Можно определить геометрическую вероятность в пространстве и на прямой:
Слайд 7: Опыт 2. В квадрат со стороной 4 см «бросают» точку. Какова вероятность, что расстояние от этой точки до ближайшей стороны квадрата будет меньше 1 см?
Закрасим в квадрате множество точек, удаленных от ближайшей стороны меньше, чем на 1 см. Площадь закрашенной части квадрата 16см 2 – 4см 2 = 12см 2. Значит,
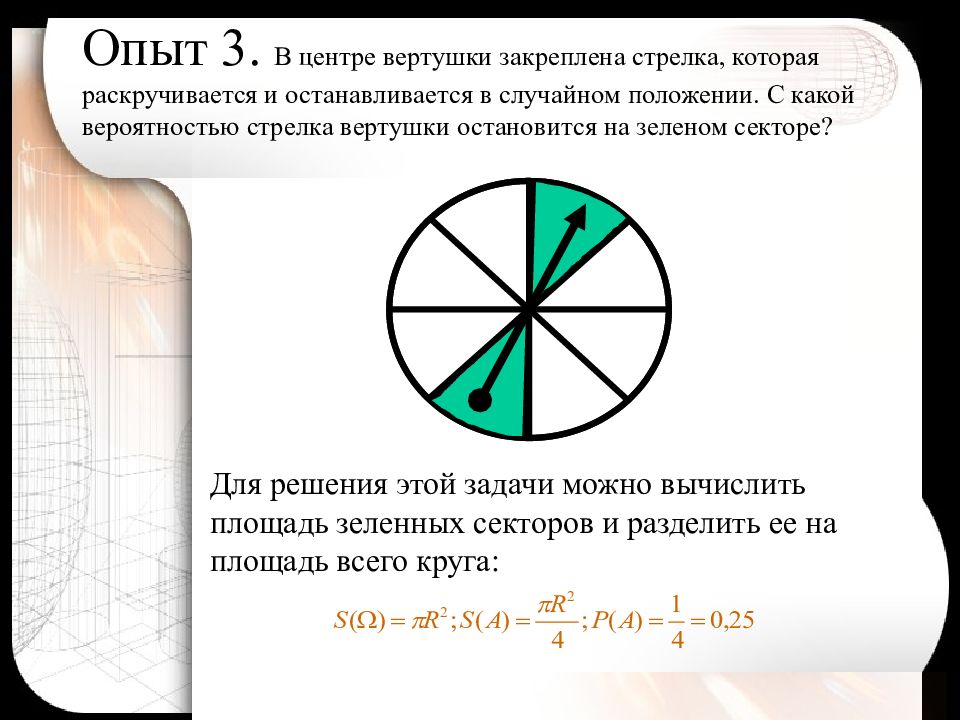
Для решения этой задачи можно вычислить площадь зеленных секторов и разделить ее на площадь всего круга:
Слайд 10: Задача №1. Дано: АВ =12см, АМ =2см, МС =4см. На отрезке АВ случайным образом отмечается точка Х. Какова вероятность того, что точка Х попадет на отрезок: 1) АМ ; 2) АС ; 3) МС ; 4) МВ ; 5) АВ ?
Решение. A ={точка Х попадает на отрезок АМ }, АМ =2см, АВ =12см, 2) В ={точка Х попадает на отрезок АС }, АС =2см+4см=6см, 3) С ={точка Х попадает на отрезок МС }, МС =4см, АВ =12см, 4) D={ точка Х попадает на отрезок МВ }, МВ =12см–2см=10см, 5) Е= { точка Х попадает на отрезок АВ }, А М С В 12 2 4
Слайд 11: Задача №2. В круг радиуса R наугад брошена точка. Найти вероятность того, что эта точка окажется внутри данного вписанного правильного треугольника
Решение. A B C K K E – событие, состоящее в том что точка К попадет в ∆ ABC Ответ: P(E) 0,41
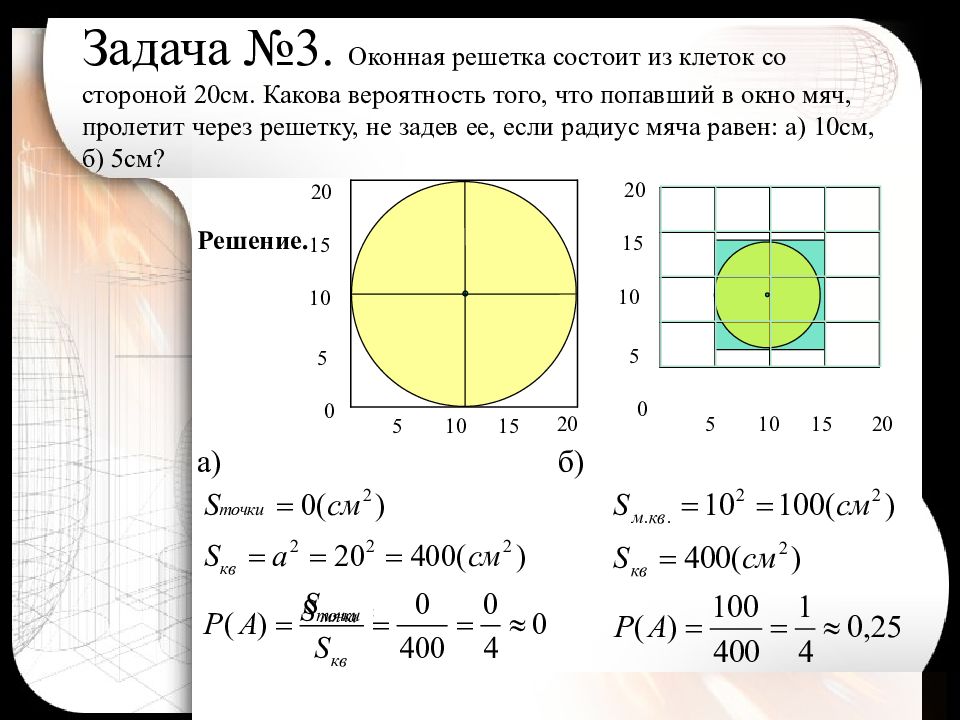
Слайд 12: Задача №3. Оконная решетка состоит из клеток со стороной 20см. Какова вероятность того, что попавший в окно мяч, пролетит через решетку, не задев ее, если радиус мяча равен: а) 10см, б) 5см?
Решение. а) б) 20 20 15 1 0 5 0 15 1 0 5 20 20 15 1 0 5 0 15 1 0 5
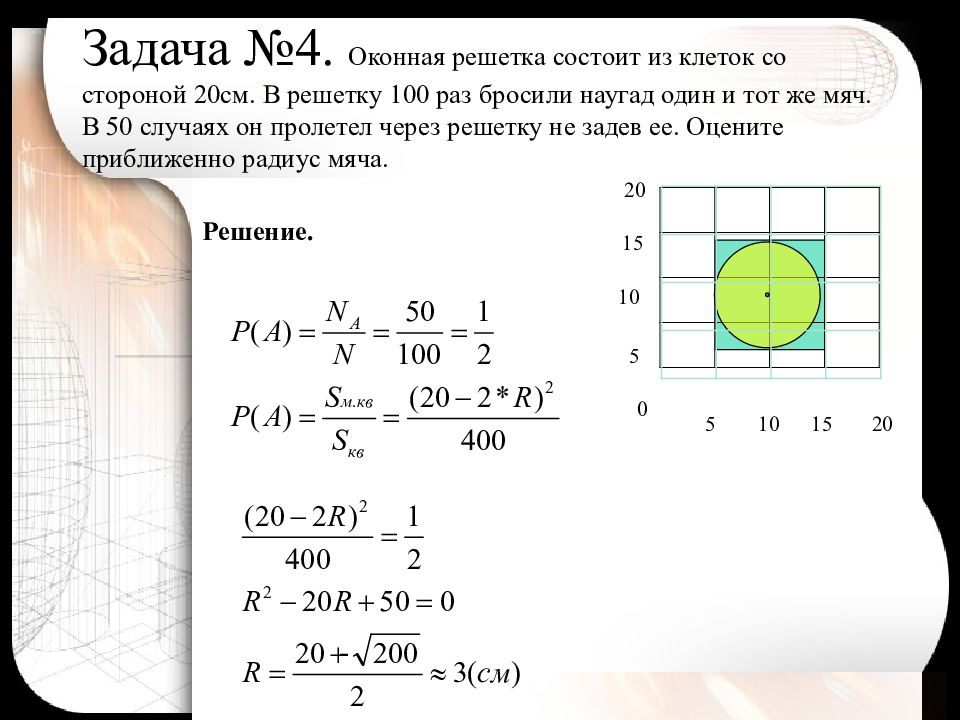
Слайд 13: Задача №4. Оконная решетка состоит из клеток со стороной 20см. В решетку 100 раз бросили наугад один и тот же мяч. В 50 случаях он пролетел через решетку не задев ее. Оцените приближенно радиус мяча
Решение. 20 20 15 1 0 5 0 15 1 0 5 -
Слайд 16: Вопросы:
Что такое геометрическая вероятность? Каковы формулы геометрической вероятности (на плоскости, на прямой, в пространстве)? Можно ли вычислить геометрические вероятности для опыта, исходы которого не являются равновозможными?
Слайд 17: Задача 1
Внутри квадрата со стороной 10см выделен круг радиусом 2см. Случайным образом внутри квадрата отмечается точка. Какова вероятность того, что она попадет в выделенный круг? А
Последний слайд презентации: Геометрическая вероятность: Задача 2
В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени длительностью Т. Моменты поступления сигналов независимы один от другого. Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t ( t < Т). Найти вероятность того, что сигнализатор срабатывает за время Т, если каждое из устройств пошлет по одному сигналу. Задача 2.