ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
НА РАВНЫЕ ЧАСТИ
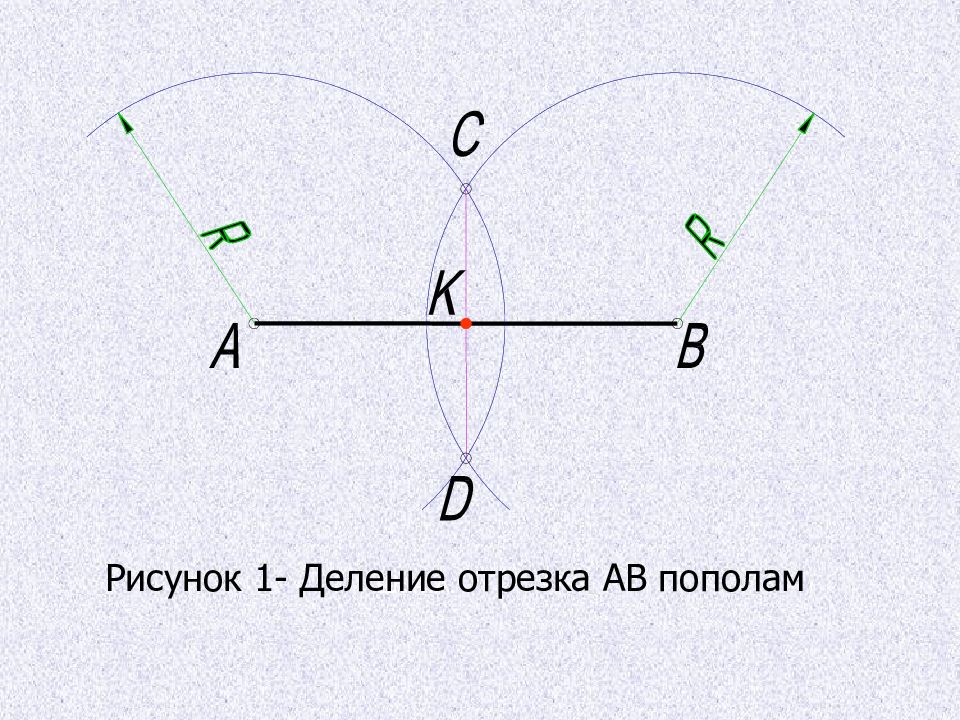
Чтобы разделить отрезок АВ пополам нужно: 1. Из концов отрезка циркулем провести две дуги окружности радиусом R, несколько большим половины данного отрезка, до взаимного пересечения; 2. Полученные точки D и С соединяют прямой, которая делит отрезок АВ пополам в точке К. 3. Прямая CD перпендикулярна отрезку АВ и проходит через его середину. Аналогично можно разделить отрезок на четыре равные части
Ш. А.А. Рисунок 1- Деление отрезка АВ пополам
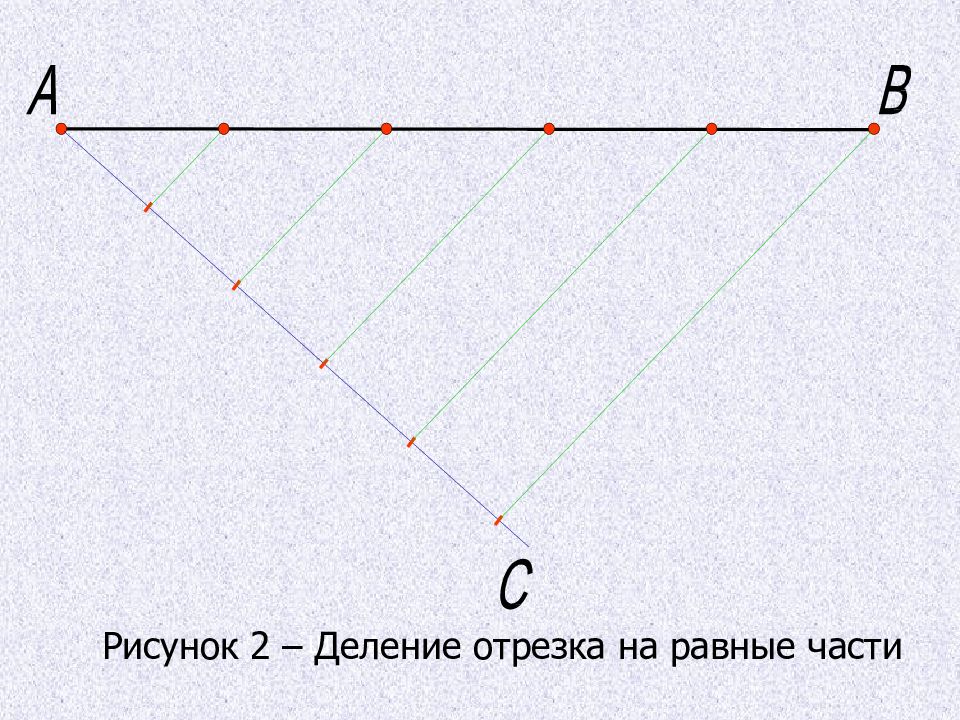
Деление отрезка АВ на несколько равных частей : Из любого конца отрезка под произвольным острым углом проводят вспомогательную прямую ВС. От вершины образовавшегося угла (т.В) на вспомогательной прямой откладывают столько одинаковых отрезков произвольной длины, на сколько частей нужно разделить данный отрезок. Конец последнего отрезка прямой линией соединяют с точкой А и параллельно этой линии через все деления проводят прямые до пересечения с прямой АВ, деля ее тем самым на заданное число равных отрезков.
Ш. А.А. Рисунок 2 – Деление отрезка на равные части
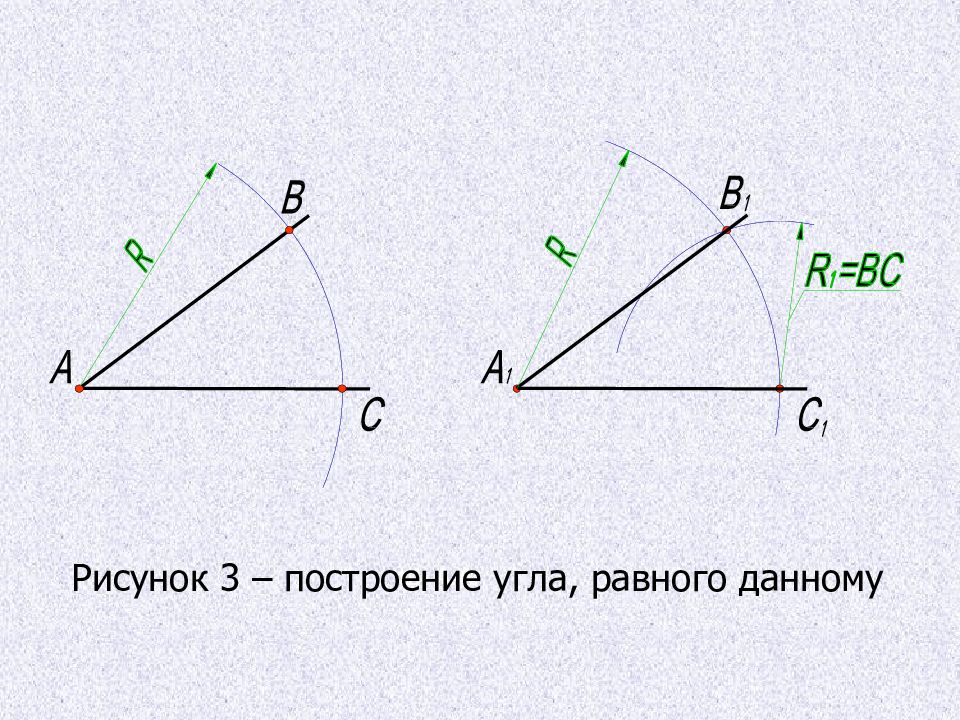
Построение угла равного данному Из вершины А заданного угла ВАС произвольным радиусом R проводят дугу до пересечения со сторонами угла в точках В и С. На произвольном поле чертежа проводят прямую линию (в данном случае горизонтальную) из точки А1 (вершины угла). Из точки А1 радиусом R, равным АВ или АС проводят дугу до пересечения с прямой, получают точку С1. Из точки С1 радиусом R 1 равным отрезку ВС, делают засечку на дуге, тем самым находят точку В1. Соединив точки А1 и В1 получают угол В1А1С1, равный данному.
Ш. А.А. Рисунок 3 – построение угла, равного данному
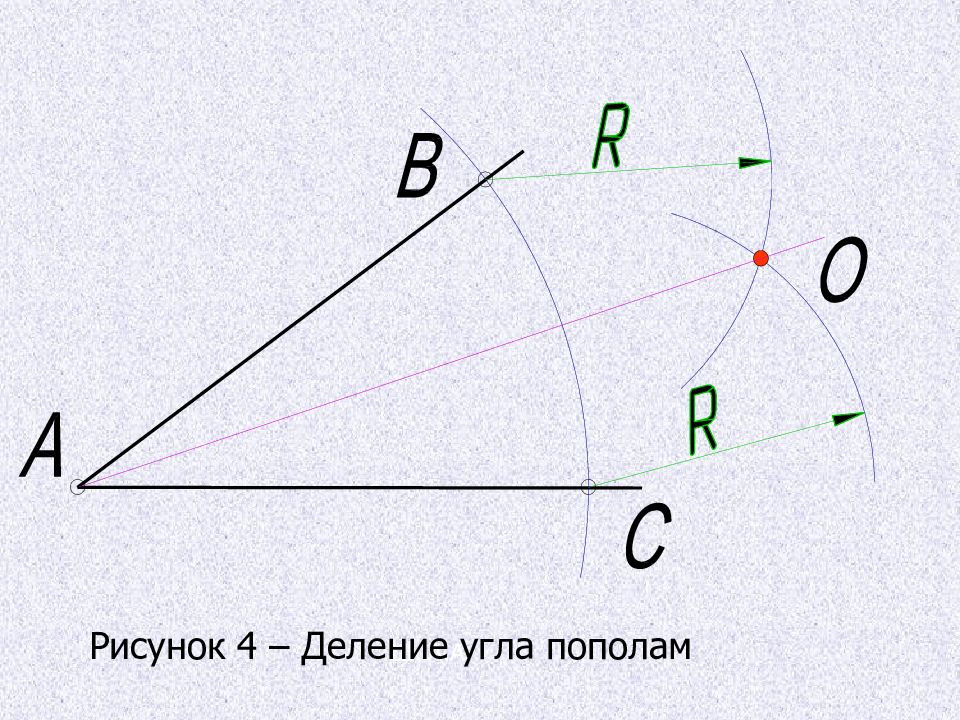
Деление угла пополам Из вершины угла произвольным радиусом проводят дугу до пересечения со сторонами угла, получая точки В и С. Из точек В и С проводят две дуги радиусом больше половины расстояния ВС до их пересечения в точке Д. Соединив точки А и Д прямой, получают биссектрису угла, которая делит угол пополам. Деление угла на четыре равные части осуществляется путем последовательного деления полученных углов ВАД и ДАС пополам вышеописанным способом.
Ш. А.А. Рисунок 4 – Деление угла пополам
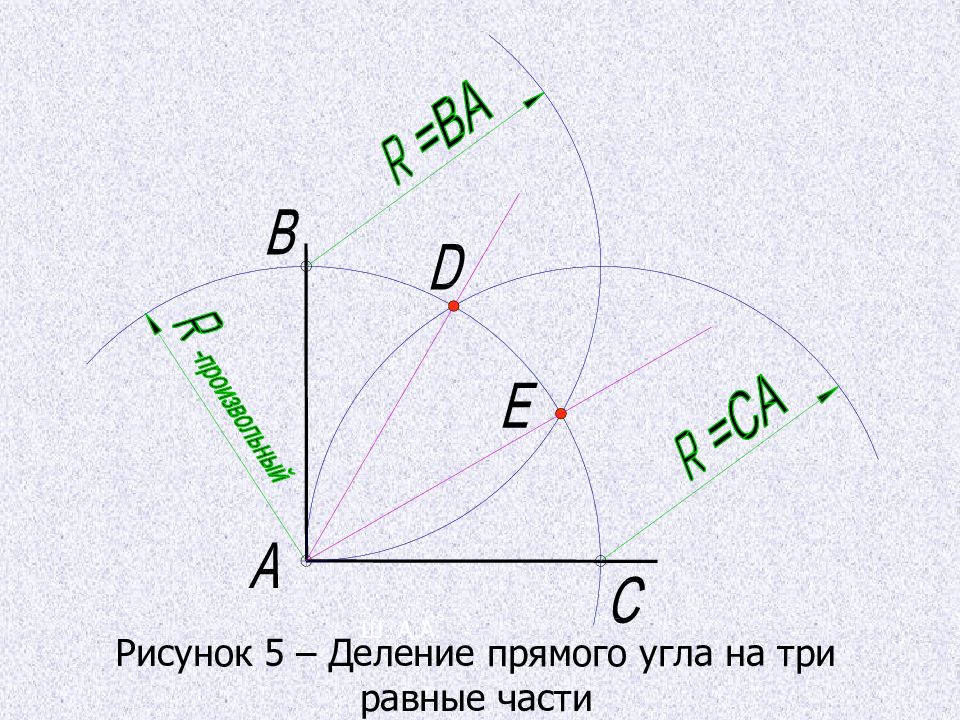
Деление прямого угла на три равные части Из вершины А произвольным радиусом проводят дугу до пересечения со сторонами угла в точках В и С. Тем же радиусом из точек В и С делают на дуге засечки, получают точки D и Е, которые соединяют с точкой А. Прямые А D и АЕ делят прямой угол на три равные части.
Ш. А.А. Рисунок 5 – Деление прямого угла на три равные части
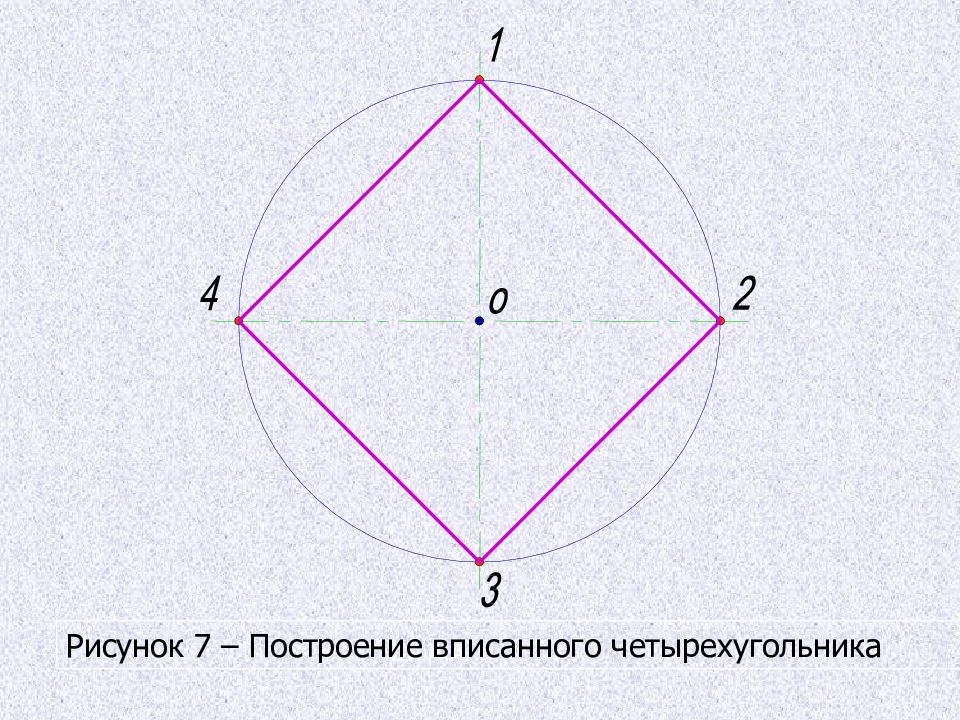
Деление окружности на четыре равные части Построение правильного вписанного четырех угольника Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части. Соединив точки пересечения этих линий с окружностью прямыми, получают правильный вписанный четырехугольник.
Ш. А.А. Рисунок 7 – Построение вписанного четырехугольника
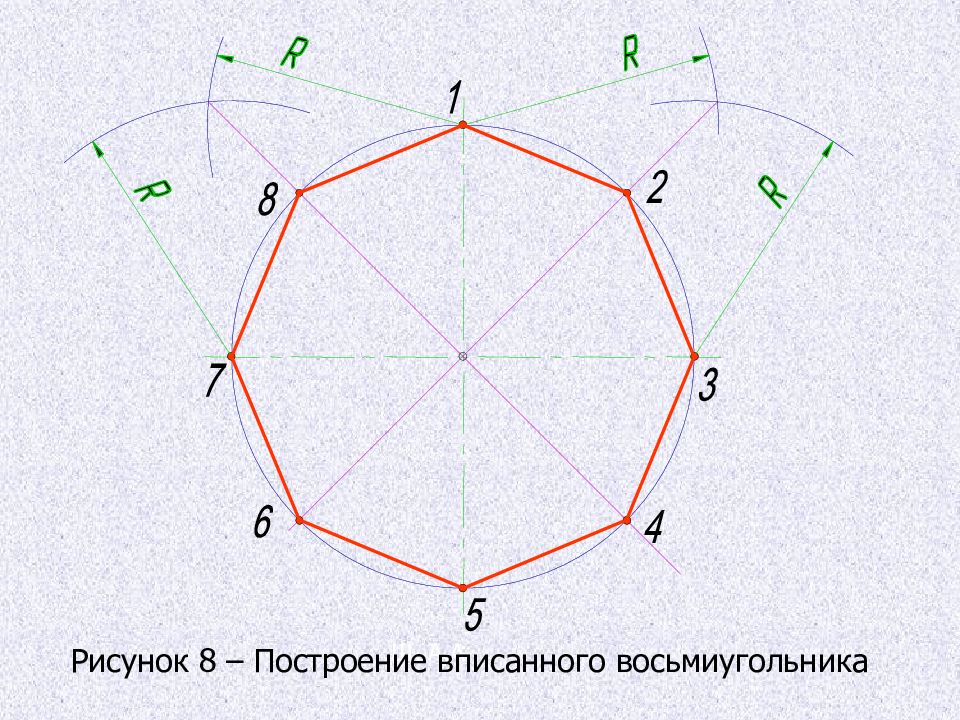
Деление окружности на восемь равных частей, построение правильного вписанного восьмиугольника 1. Из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом R проводят дуги до взаимного пересечения; 2.Тем же радиусом из точки 5 делают засечку на дуге проведенной из точки 3. 3. Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8. 4. Полученные восемь точек соединить последовательно прямыми линиями, получится правильный вписанный восьмиугольник.
Ш. А.А. Рисунок 8 – Построение вписанного восьмиугольника
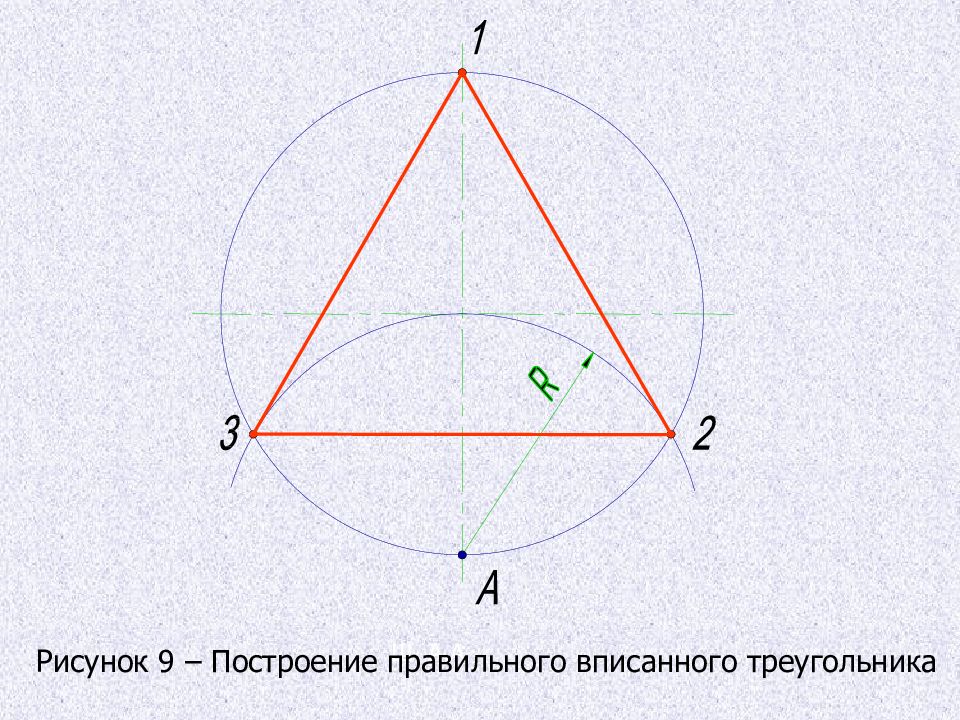
Деление окружности на три равные части, построение правильного вписанного треугольника Из любой точки окружности, например точки А пересечения центровых линий с окружностью, проводят дугу радиусом R, равным радиусу окружности, получают точки 2 и 3. Третья точка деления (точка 1) будет находится на противоположном конце диаметра, проходящего через точку А. Последовательно соединив точки 1, 2 и 3, получают правильный вписанный треугольник.
Ш. А.А. Рисунок 9 – Построение правильного вписанного треугольника
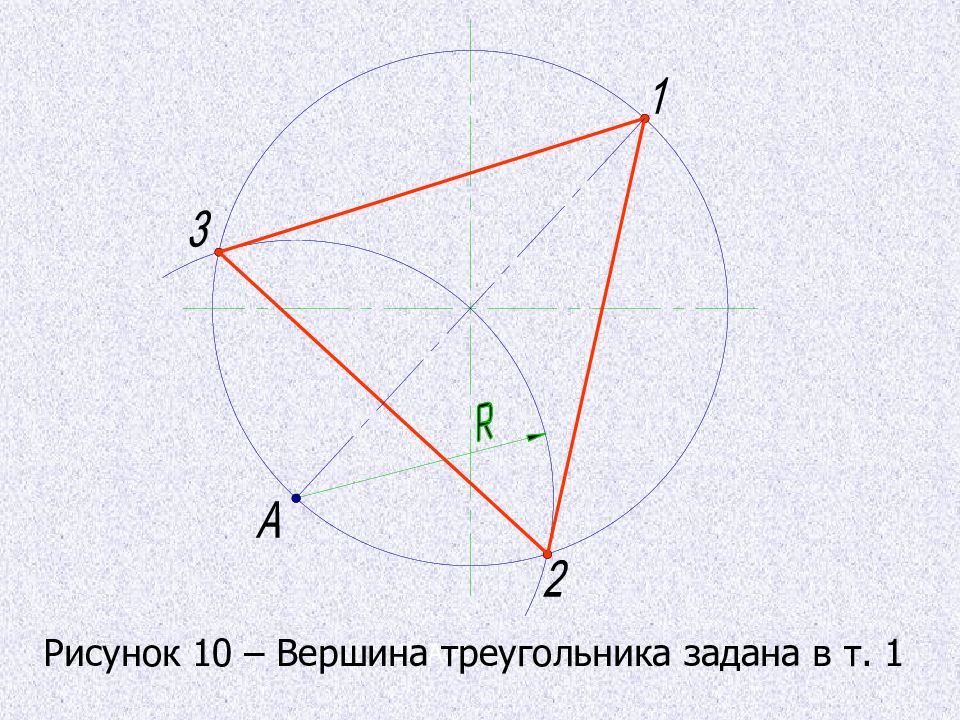
Если одна из вершин правильного вписанного треугольника задана, напр. точка 1 - находят точку А 1.Через заданную точку проводят диаметр. 2. Точка А будет находится на противоположном конце этого диаметра. 3. Затем проводят дугу радиусом R, равным радиусу данной окружности, получают точки 2 и
Ш. А.А. Рисунок 10 – Вершина треугольника задана в т. 1
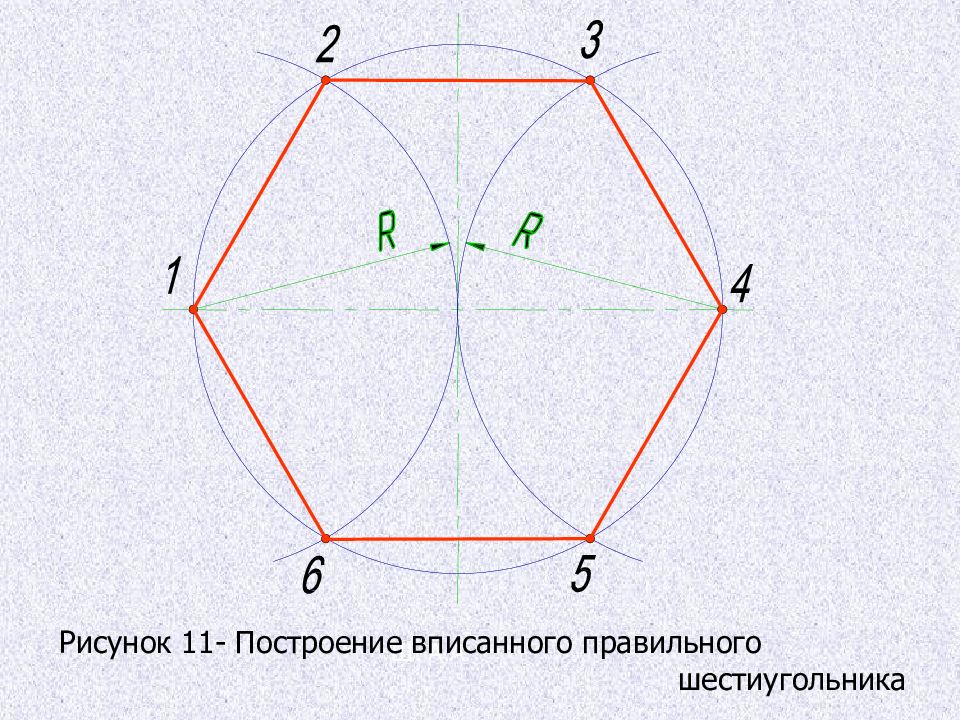
Деление окружности на шесть равных частей, построение правильного вписанного шестиугольника Из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5. Последовательно соединив полученные точки, получают правильный вписанный шести угольник
Ш. А.А. Рисунок 11- Построение вписанного правильного шестиугольника
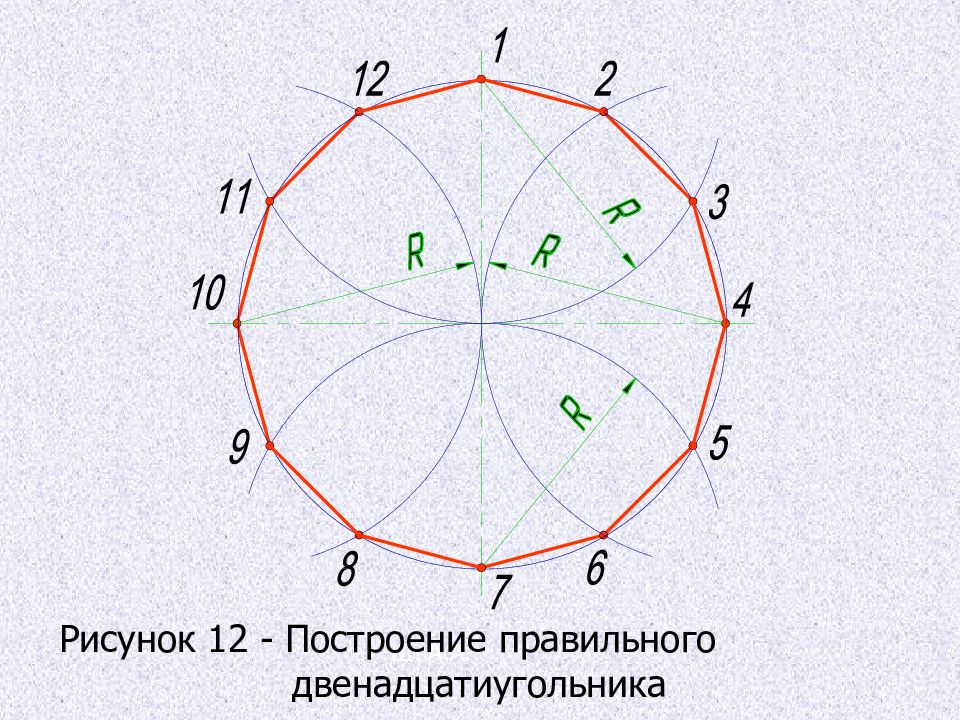
Деление окружности на двенадцать равных частей, построение правильного вписанного двенадцатиугольника 1. Из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью. 2. Соединив последовательно полученные точки пересечения получают правильный вписанный двенадцатиугольник.
Ш. А.А. Рисунок 12 - Построение правильного двенадцатиугольника
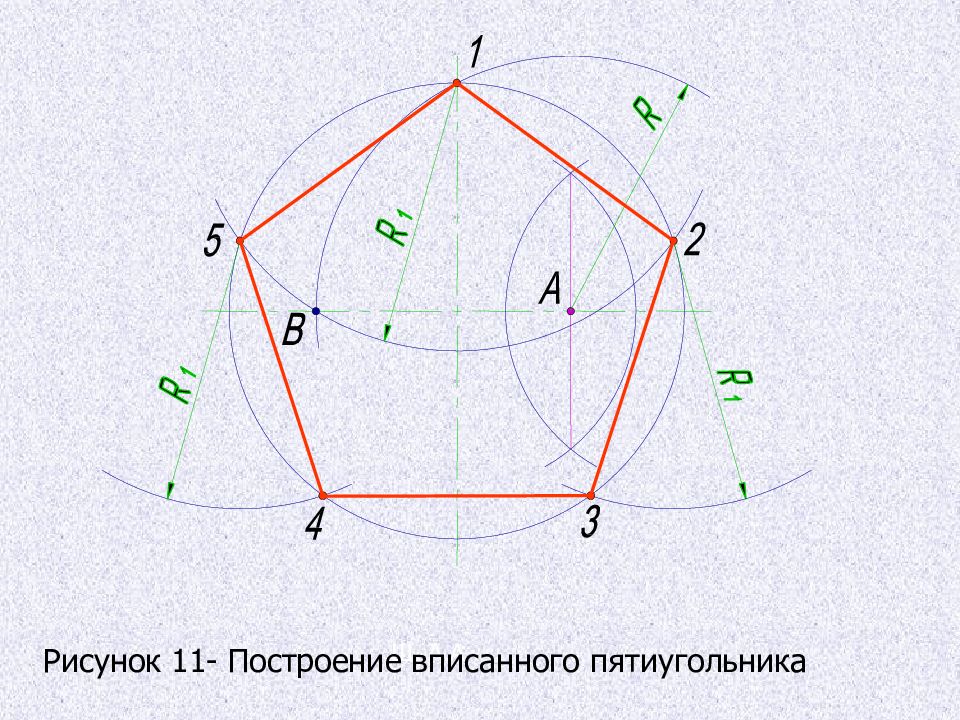
Деление окружности на пять равных частей, построение правильного вписанного пятиугольника 1. Половину любого диаметра (радиуса) делят пополам, получают точку А. 2. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра в точке В. 3. Отрезок 1В равен хорде стягивающей дугу, длина которой равна 1/5 длины окружности. 4. Делая засечки на окружности радиусом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку А выбирают в зависимости от расположения пятиугольника.
4. Из точки 1 строят точки 2 и 5, затем из точки 2 строят точку 3, а из точки 5 строят точку 4. 5. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит накопление погрешностей измерения и последняя сторона пятиугольника получается перекошенной. 6. Последовательно соединив найденные точки, получают правильный вписанный пятиугольник.
Ш. А.А. Рисунок 11- Построение вписанного пятиугольника
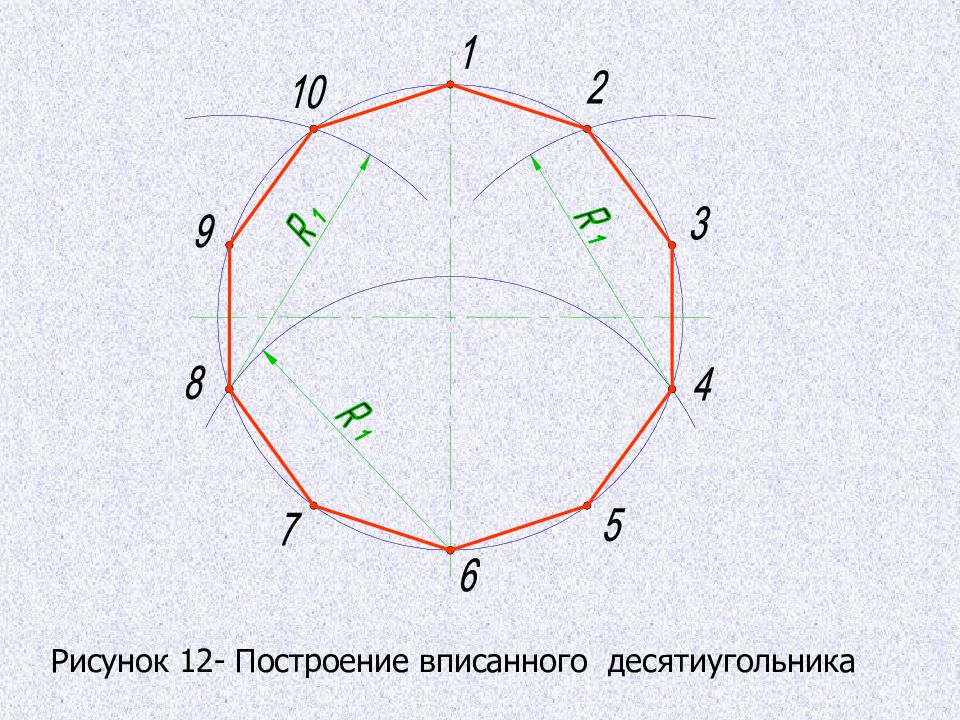
Деление окружности на десять равных частей, построение правильного вписанного десятиугольника Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей. Делят окружность на пять равных частей, начиная построения из точки 1, затем из точки 6, находящейся на противоположном конце диаметра. Соединив последовательно все точки, получают правильный вписанный десятиугольник.
Рисунок 12- Построение вписанного десятиугольника
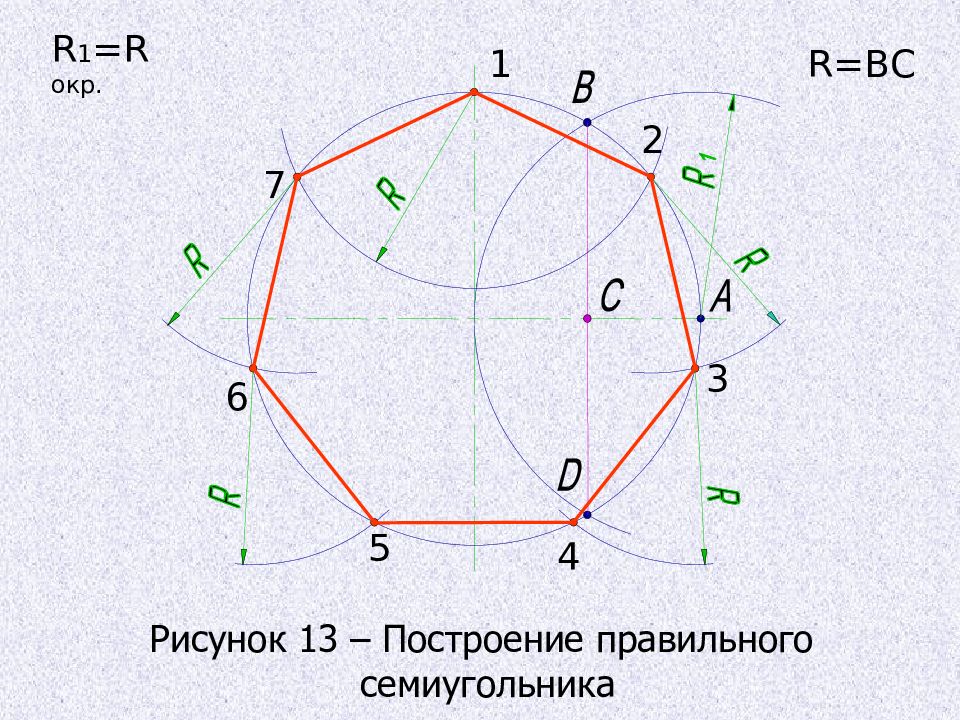
Деление окружности на семь равных частей, построение правильного вписанного семиугольника Из любой точки окружности, например точки А, радиусом заданной окружности проводят дугу до пересечения с окружностью в точках B и D прямой. Половина полученного отрезка ( в данном случае отрезок ВС ) будет равен хорде, которая стягивает дугу, составляющую 1/7 длины окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной при построении правильного пятиугольника. Соединив последовательно все точки, получают правильный вписанный семиугольник.
1 2 3 4 5 6 7 R 1 =R окр. R= ВС Рисунок 13 – Построение правильного семиугольника
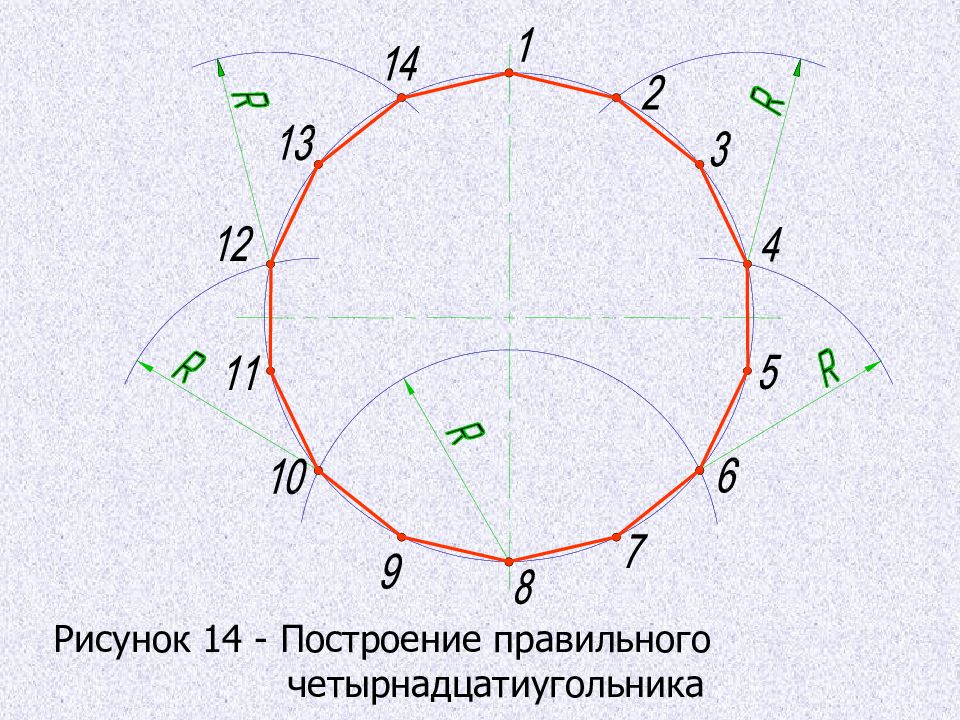
Деление окружности на четырнадцать равных частей, построение правильного вписанного четырнадцатиугольника Построения выполняют аналогично делению окружности на семь равных частей, но сначала делят окружность на семь равных частей, начиная построения из точки 1, а затем из точки 8, находящейся на противоположном конце диаметра. 2. Соединив последовательно все точки, получают правильный вписанный четырнадцатиугольник.
Рисунок 14 - Построение правильного четырнадцатиугольника
Деление окружности на любое количество равных частей с помощью таблицы хорд
4. ПОСТРОЕНИЕ СОПРЯЖЕНИЙ Касание -плавный переход одной линии в другую Сопряжение - плавный переход одной линии в другую, выполненный при помощи промежуточной линии. Чаще всего промежуточной линией служит дуга окружности.
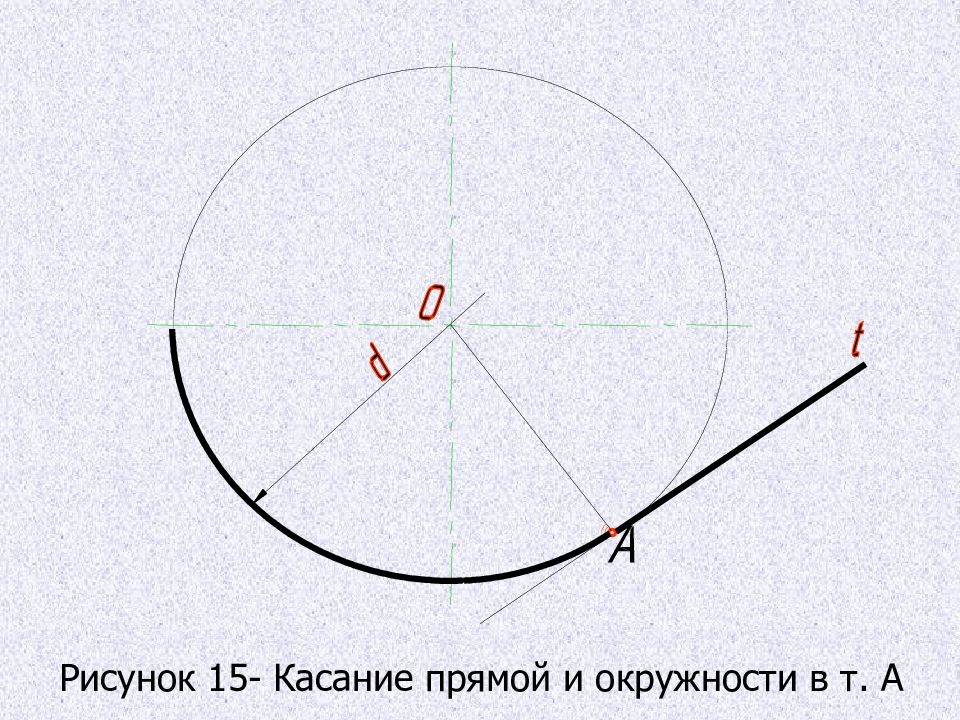
Построение сопряжений основано на следующих геометрических положениях: а ) переход окружности на прямую только тогда будет плавным, когда данная прямая является касательной к окружности. Радиус окружности, проведенный в точку касания А, перпендикулярен к касательной прямой t ;
Рисунок 15- Касание прямой и окружности в т. А
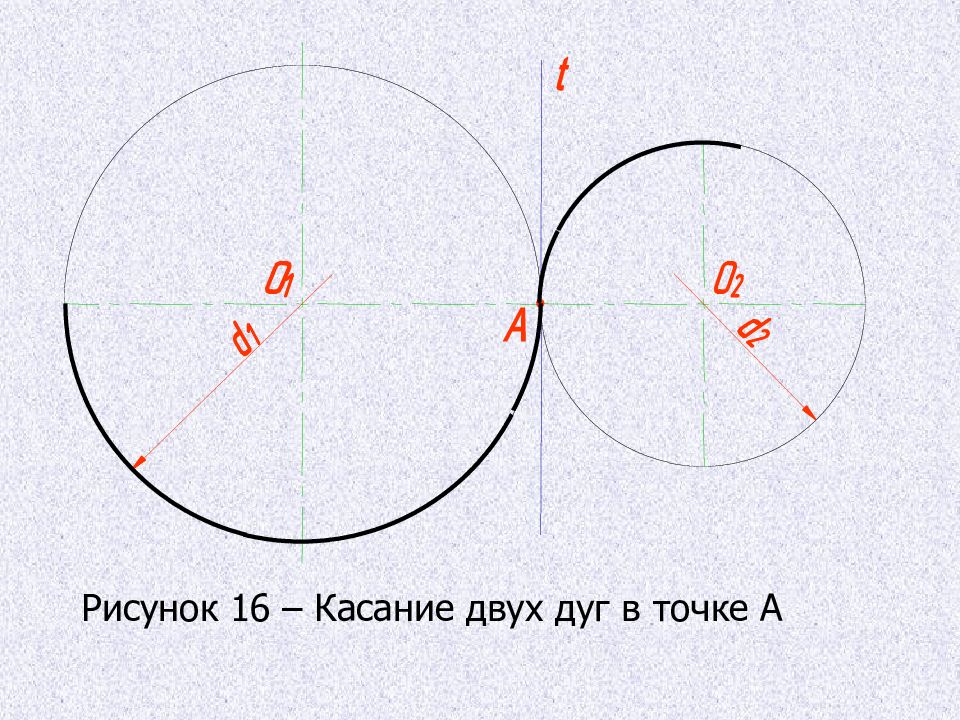
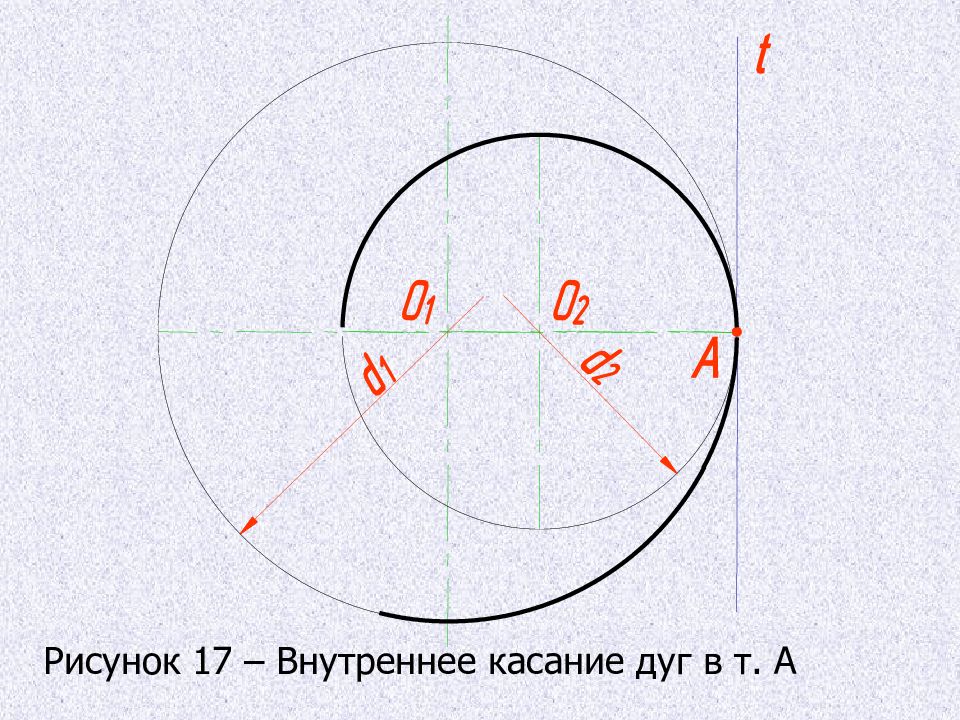
б ) переход в данной точке А с одной окружности на другую только тогда будет плавным, когда окружности имеют в данной точке общую касательную. Точка касания А и центры окружностей О 1 и О 2 лежат на одной прямой. Касание называется внешним, если центры О 1 и О 2 лежат по разные стороны от касательной t и внутренним, если центры находятся по одну сторону об общей касательной.
Рисунок 16 – Касание двух дуг в точке А
Рисунок 17 – Внутреннее касание дуг в т. А
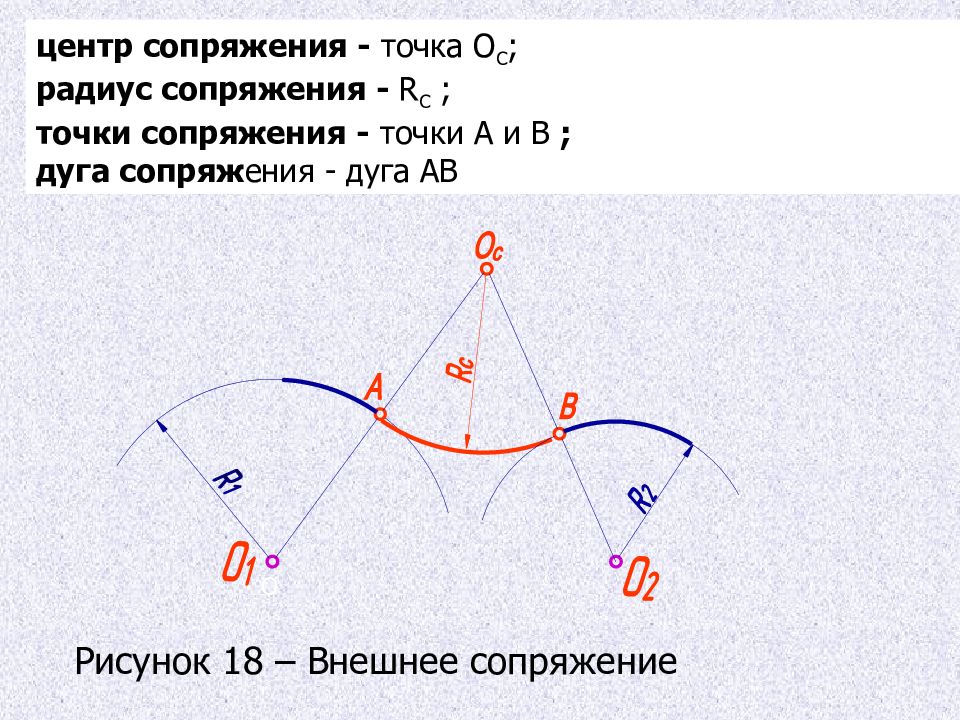
центр сопряжения - точка О С ; радиус сопряжения - R С ; точки сопряжения - точки А и В ; дуга сопряж ения - дуга АВ О Рисунок 18 – Внешнее сопряжение
Алгоритм построения сопряжений двух линий при заданном радиусе сопряжения 1. Построить геометрическое место точек, удаленных от на расстоянии радиуса сопряжения от первой из сопрягаемых линий. 2. Построить геометрическое место точек, удаленных от на расстоянии радиуса сопряжения от второй из сопрягаемых линий. На пересечении данных геометрических мест определить центр сопряжения. Определить точку сопряжения на первой из сопрягаемых линий. Определить точку сопряжения на второй из сопрягаемых линий. 6.В границах между точками сопряжений провести дугу сопряжения.
4.1 СОПРЯЖЕНИЕ ДВУХ ПРЯМЫХ ЛИНИЙ
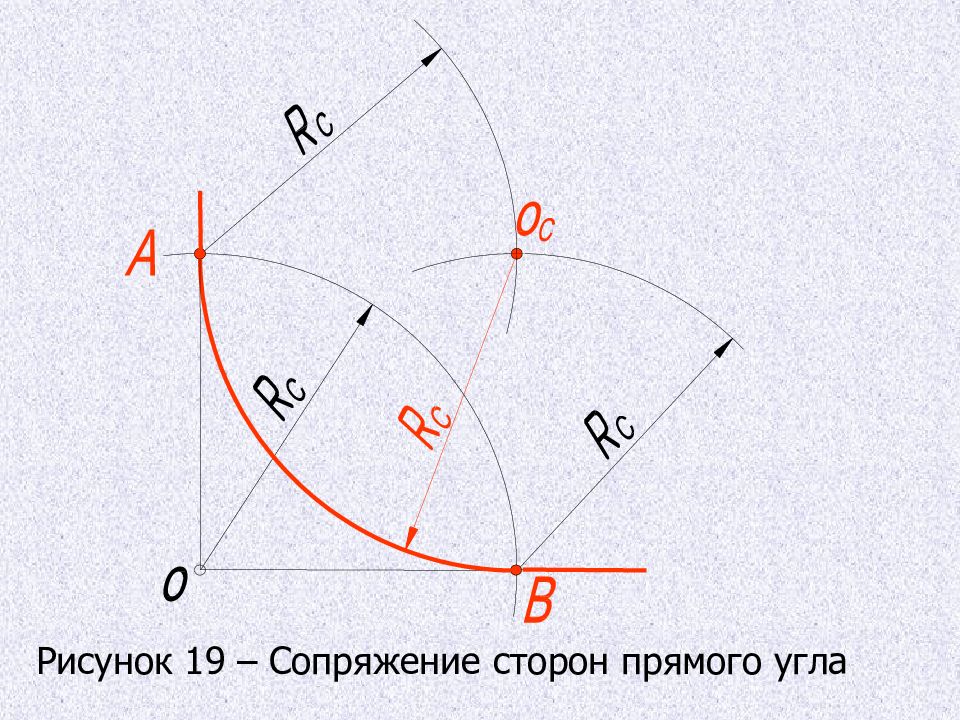
СОПРЯЖЕНИЕ СТОРОН ПРЯМОГО УГЛА 1. Из вершины О прямого угла проводят дугу окружности R C и получают точки сопряжения А и В. 2. Центр сопряжения находится на пересечении дуг, проведенных из точек А и В, как из центров, тем же радиусом R C. 3. Из центра сопряжения О С проводят между точками А и В дугу сопряжения.
Рисунок 19 – Сопряжение сторон прямого угла
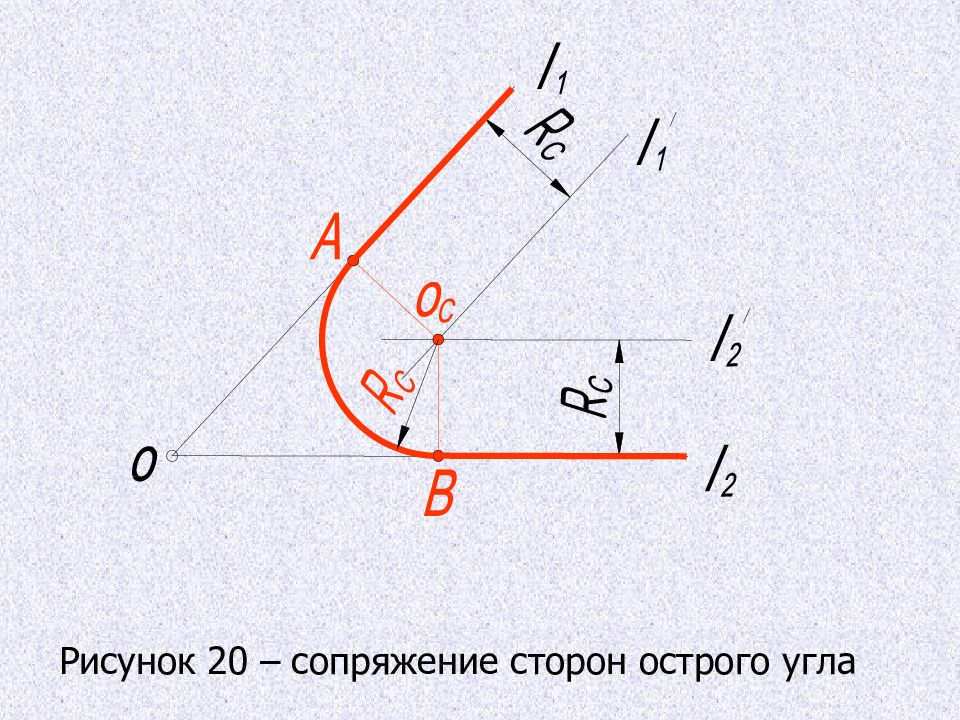
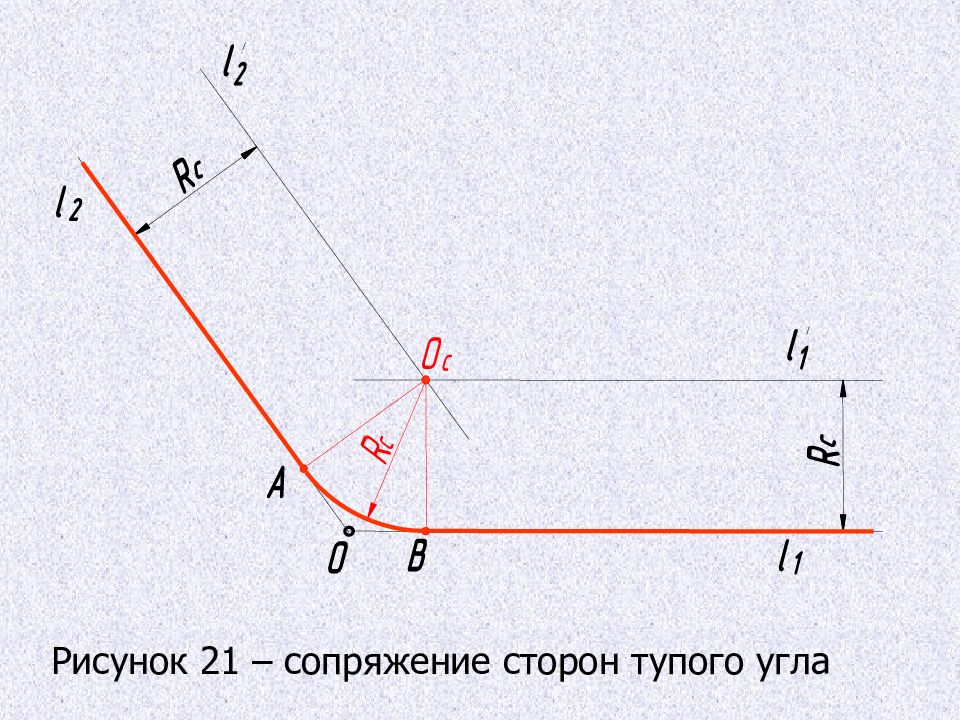
СОПРЯЖЕНИЕ СТОРОН ОСТРОГО ( ТУПОГО ) УГЛА Центр сопрягающей дуги должен быть удален от каждой из прямых на величину равную радиусу R C. Проводят две прямые l / 1 и l / 2, параллельные данным прямым l 1 и l 2 и удаленные от них на расстояние R C. Пересечение этих прямых - точка О С – есть центр сопряжения. Опускают из центра О С перпендикуляры на стороны угла и получают точки сопряжения А и В.
Рисунок 20 – сопряжение сторон острого угла
Рисунок 21 – сопряжение сторон тупого угла
Рисунок 65 НАРУЖНЕЕ СОПРЯЖЕНИЕ ДУГ ОКРУЖНОСТЕЙ
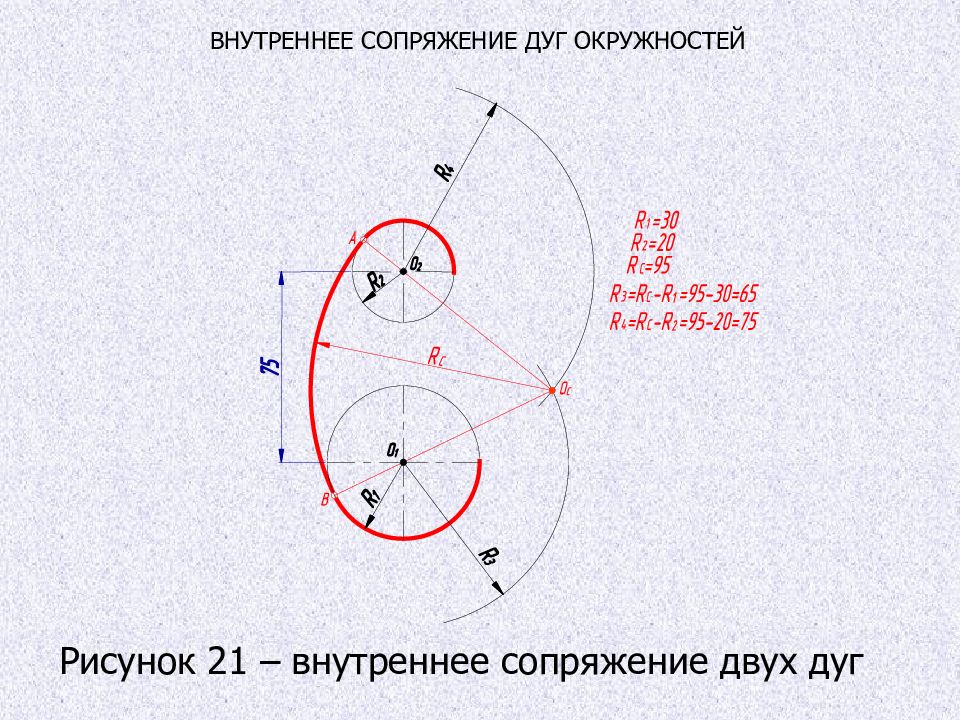
Рисунок 21 – внутреннее сопряжение двух дуг ВНУТРЕННЕЕ СОПРЯЖЕНИЕ ДУГ ОКРУЖНОСТЕЙ
КОМБИНИРОВАННОЕ СОПРЯЖЕНИЕ ДУГ ОКРУЖНОСТЕЙ Рисунок 22 -Смешанное сопряжение дуг
