Первый слайд презентации: Линии и углы в окружности
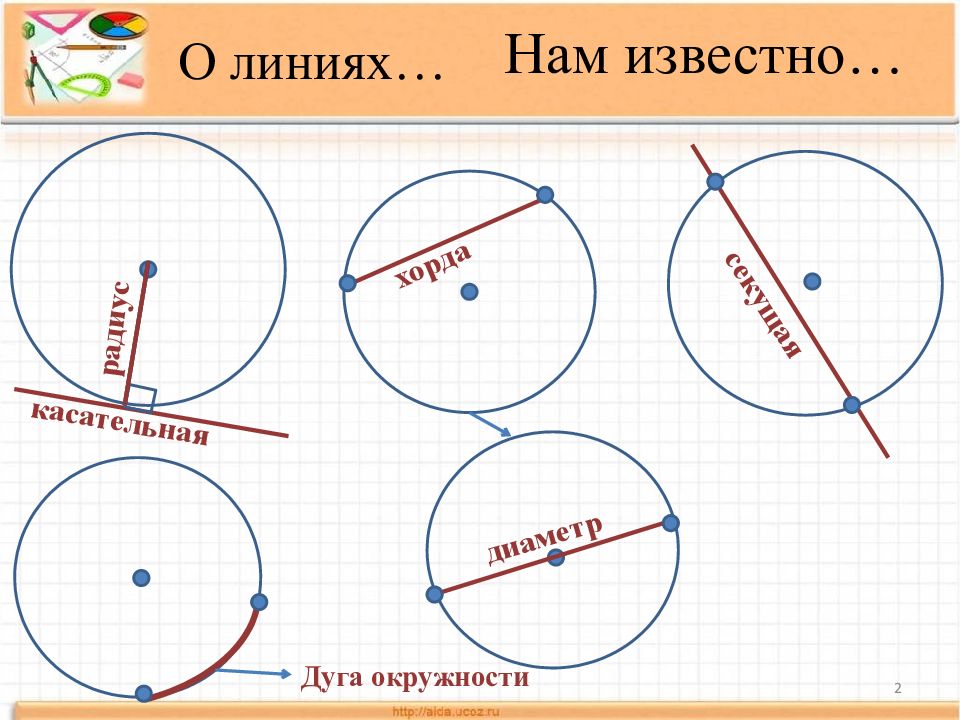
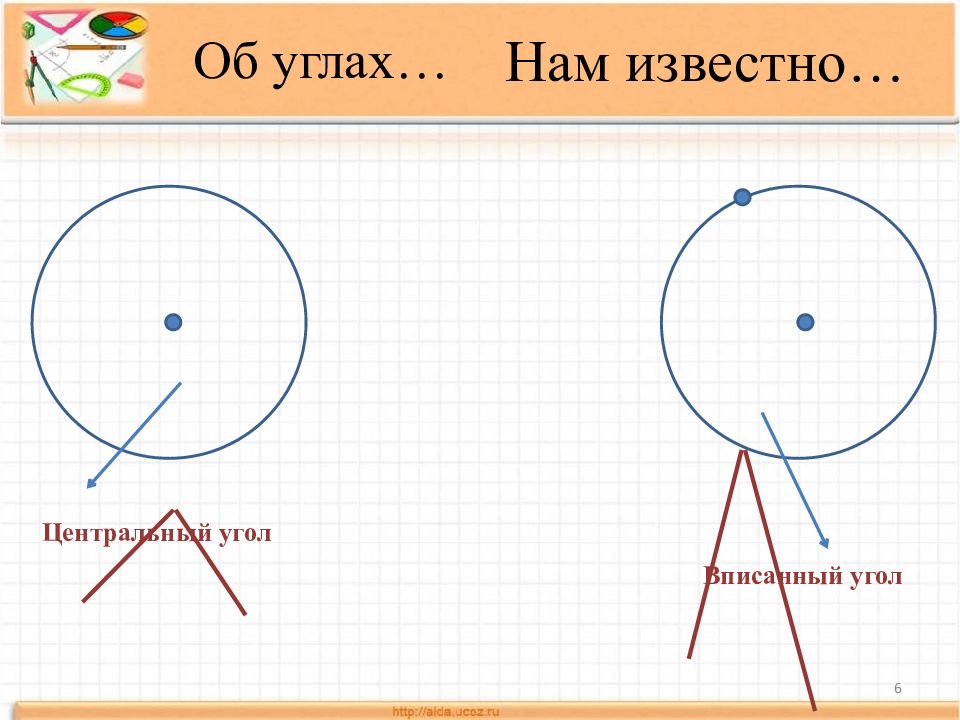
Слайд 2: Нам известно…
2 касательная диаметр секущая х орда О линиях… Дуга окружности радиус
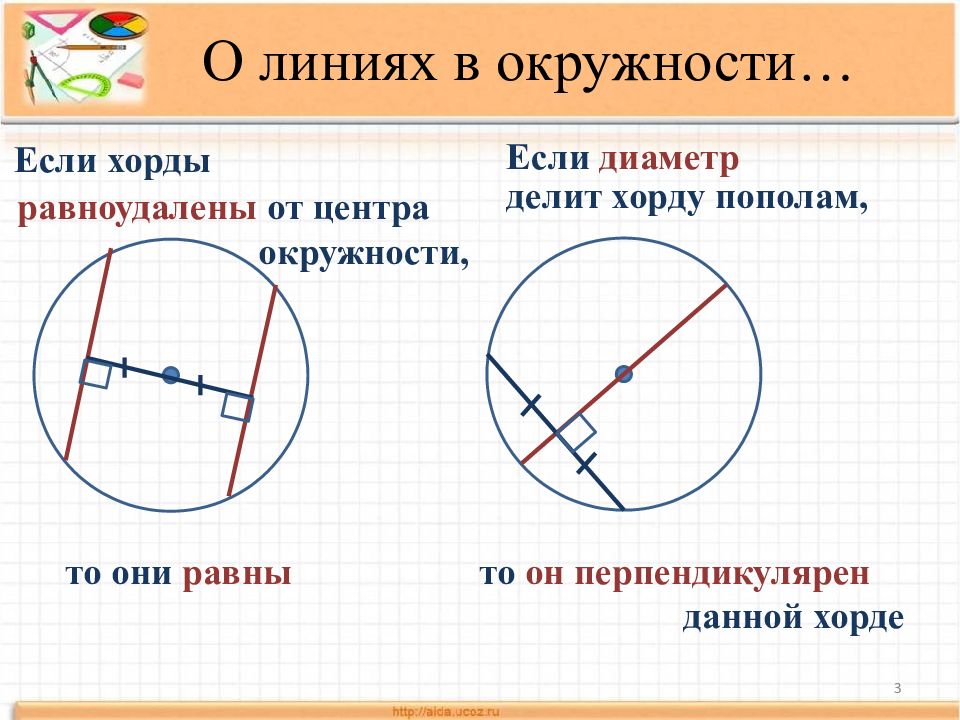
Слайд 3: О линиях в окружности…
3 Если хорды р авноудалены от центра окружности, т о они равны Если диаметр д елит хорду пополам, т о он перпендикулярен данной хорде
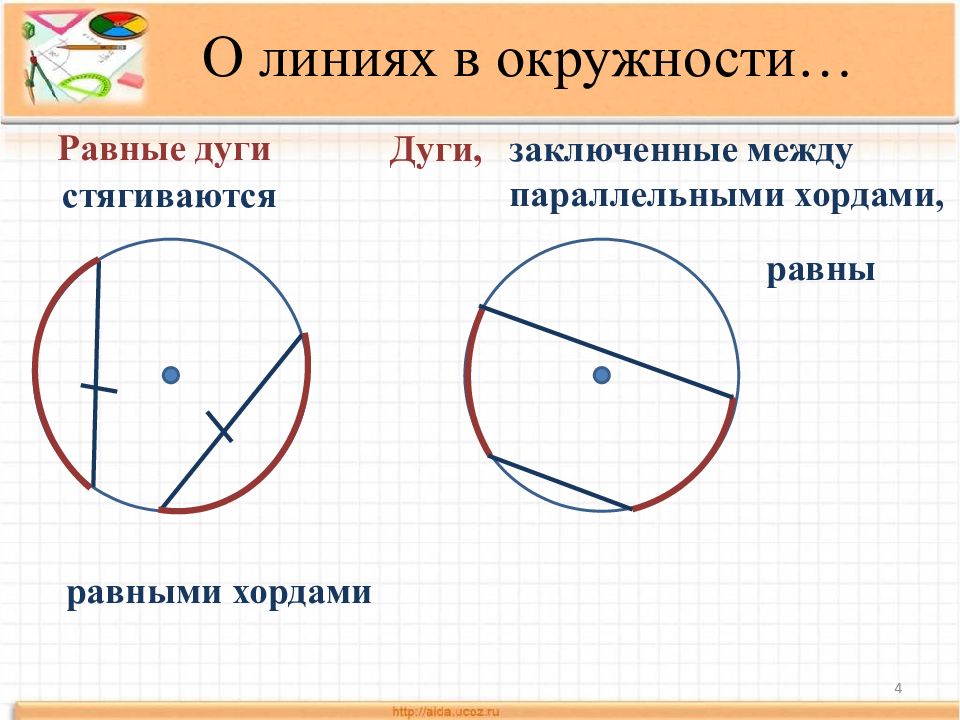
Слайд 4
4 Равные дуги стягиваются р авными хордами Дуги, заключенные между параллельными хордами, равны О линиях в окружности…
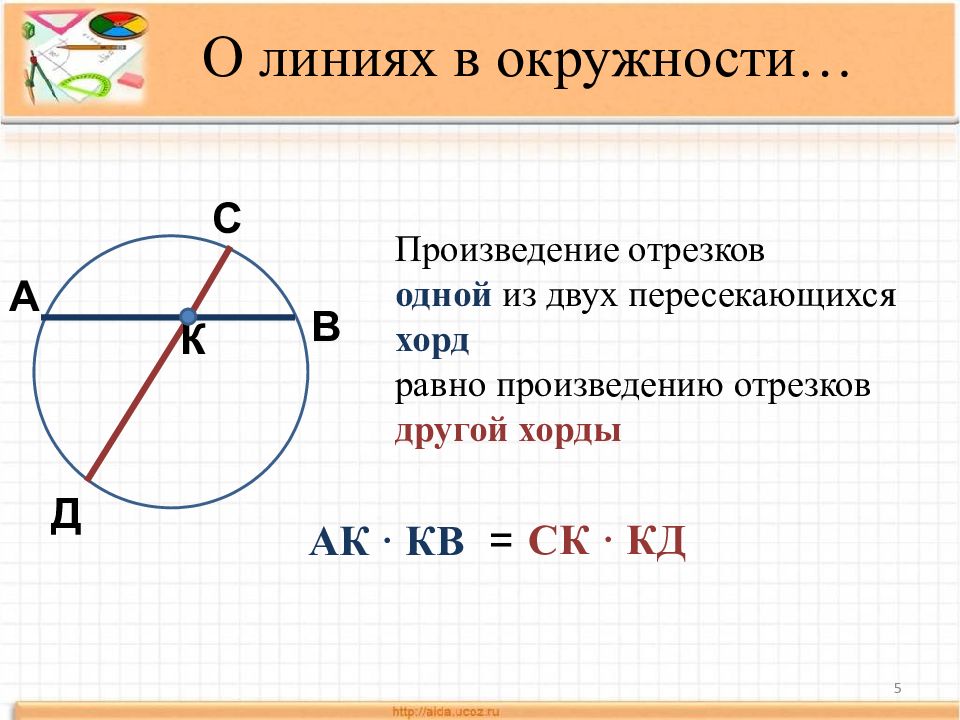
Слайд 5
5 Произведение отрезков одной из двух пересекающихся хорд равно произведению отрезков другой хорды АК · КВ В Д А С К = С К · КД О линиях в окружности…
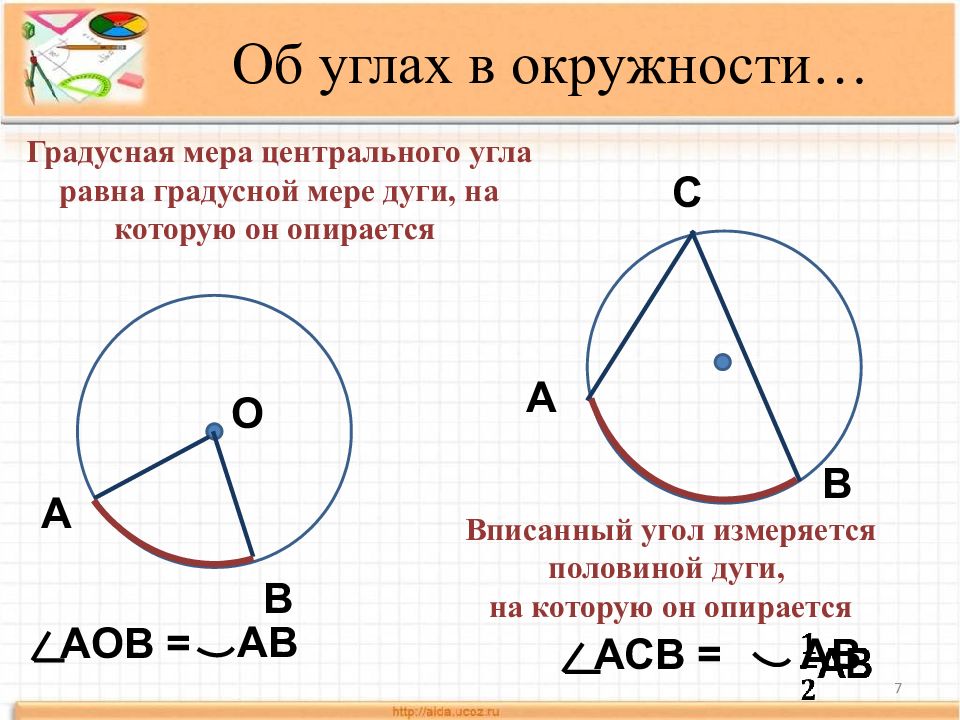
Слайд 7
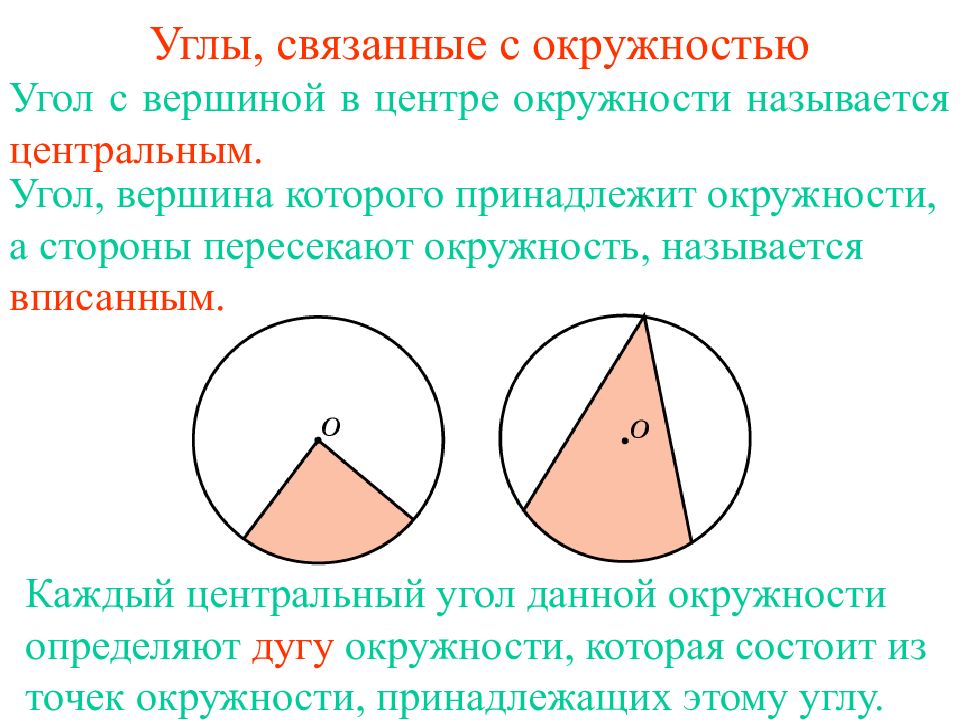
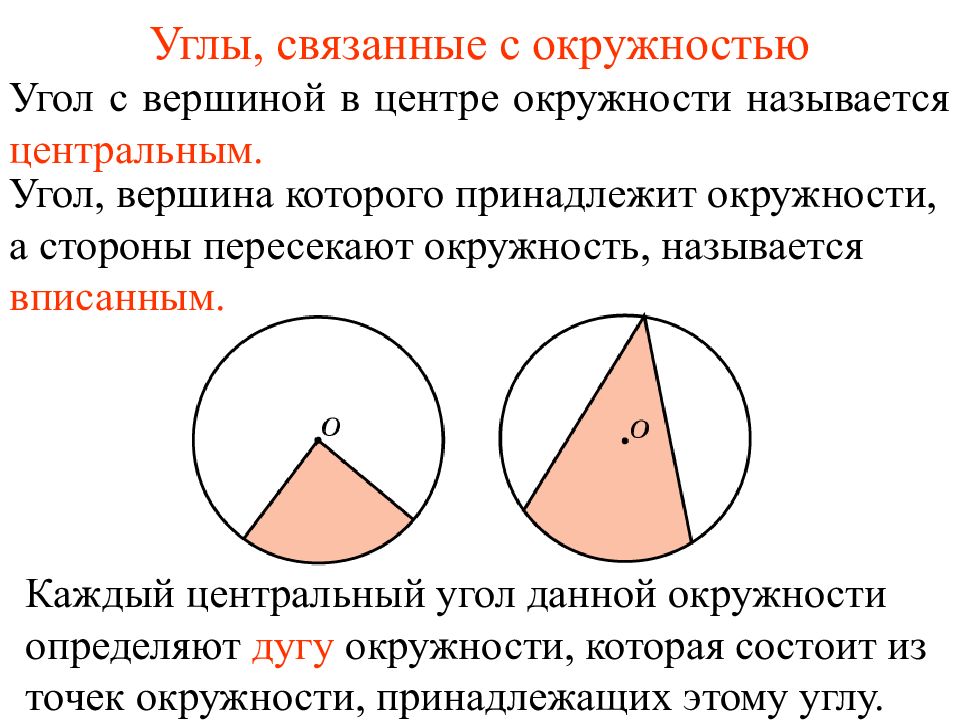
7 Об углах в окружности… Градусная мера центрального угла равна градусной мере дуги, на которую он опирается А В О Вписанный угол измеряется половиной дуги, на которую он опирается АОВ = АВ АСВ = АВ А В С
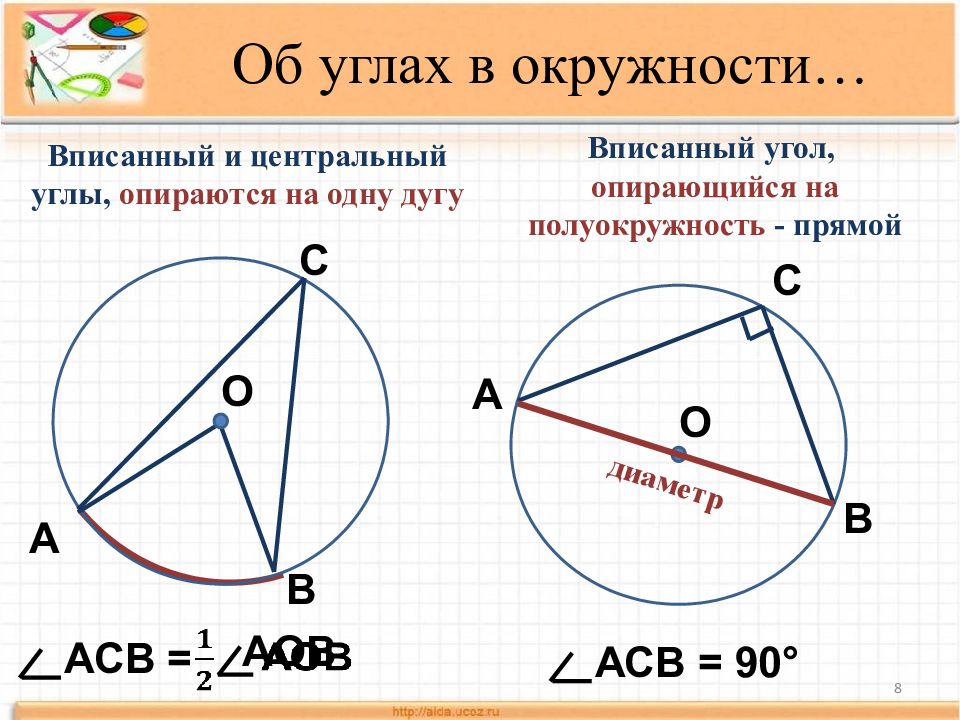
Слайд 8
8 Вписанный и центральный углы, опираются на одну дугу С А В О АСВ = АОВ А В О С Вписанный угол, опирающийся на полуокружность - прямой диаметр АСВ = 90° Об углах в окружности…
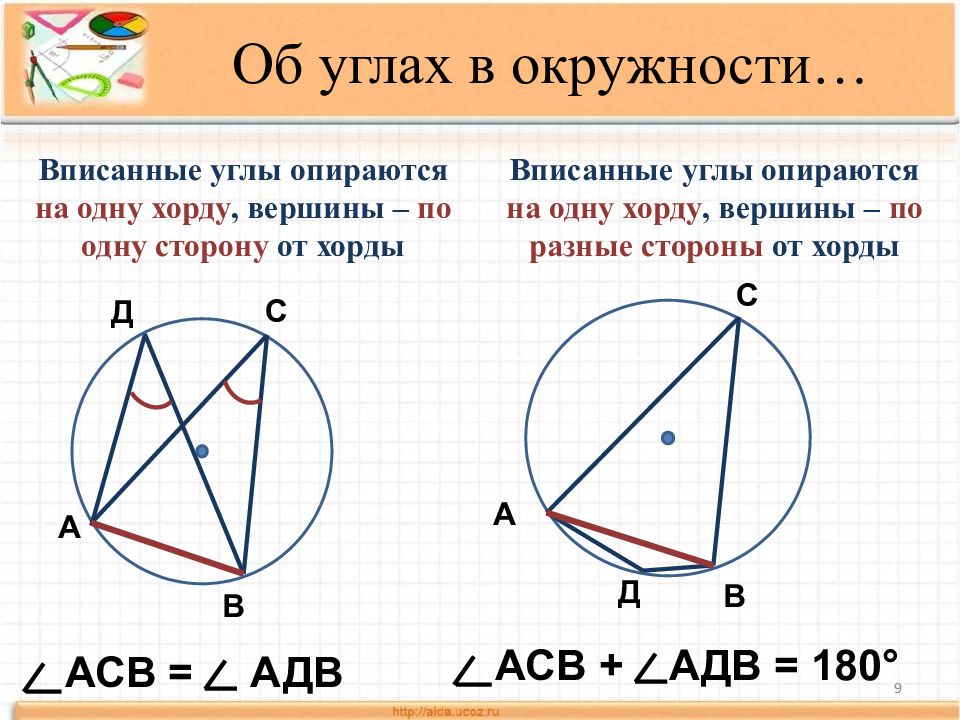
Слайд 9
9 АСВ = АДВ Вписанные углы опираются на одну хорду, вершины – по одну сторону от хорды А В С Д Д В А С Вписанные углы опираются на одну хорду, вершины – по разные стороны от хорды АСВ + АДВ = 180° Об углах в окружности…
Слайд 10
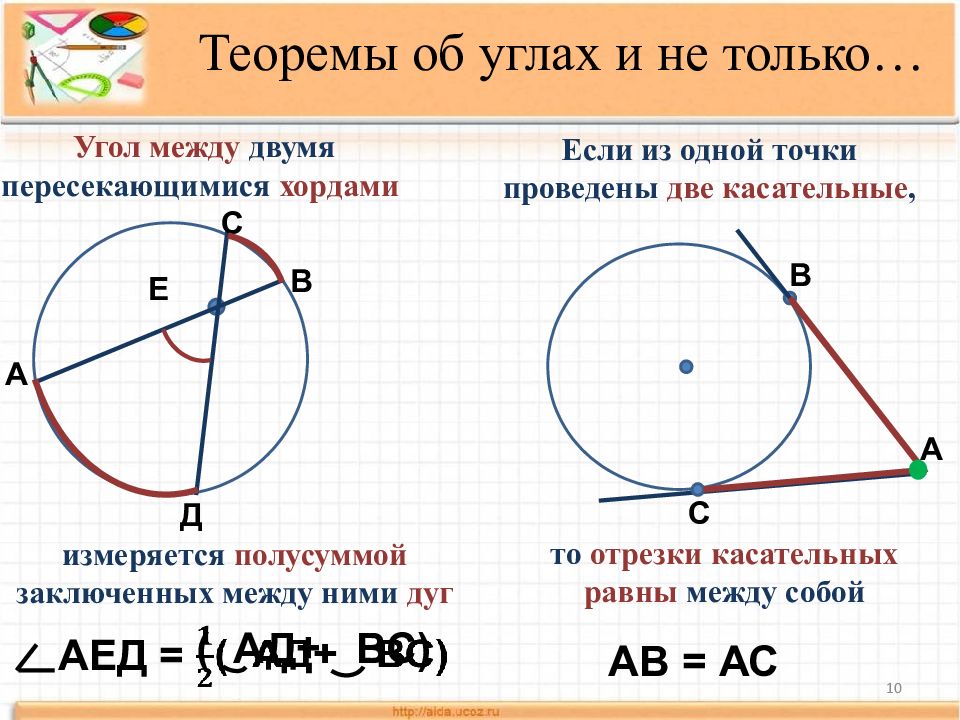
10 Теоремы об углах и не только… измеряется полусуммой заключенных между ними дуг А Д Е В С Угол между двумя пересекающимися хордами АЕД = ( АД+ ВС) Если из одной точки проведены две касательные, т о отрезки касательных равны между собой А В С АВ = АС
Слайд 11
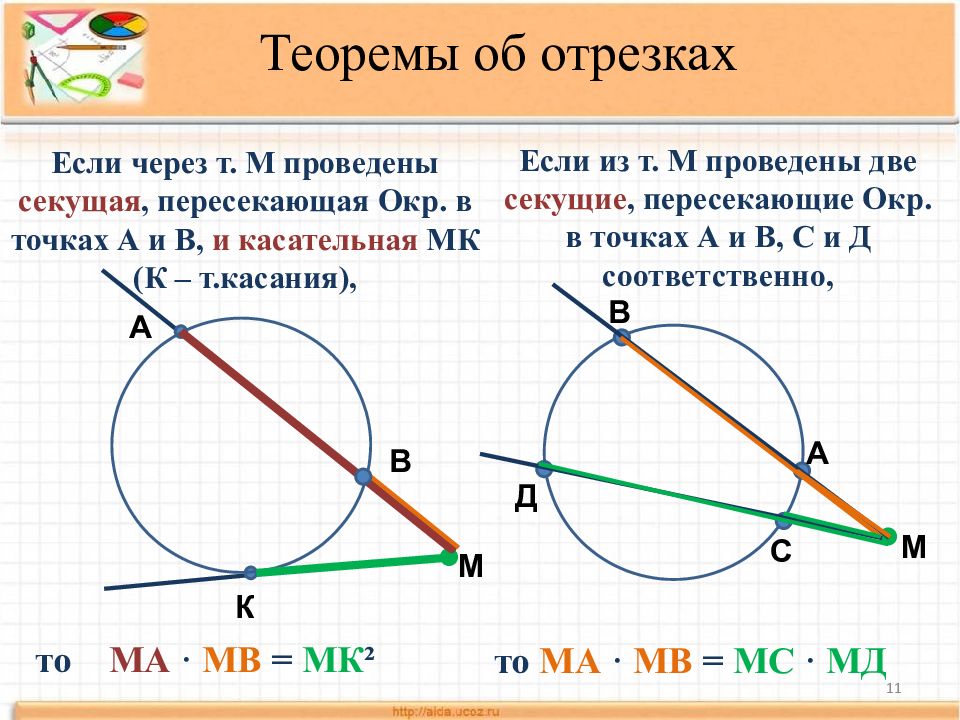
Теоремы об отрезках А М В Если через т. М проведены секущая, пересекающая Окр. в точках А и В, и касательная МК (К – т.касания ), то МА · МВ = МК ² К Если из т. М проведены две секущие, пересекающие Окр. в точках А и В, С и Д соответственно, то МА · МВ = МС · МД М В С Д А 11
Слайд 12
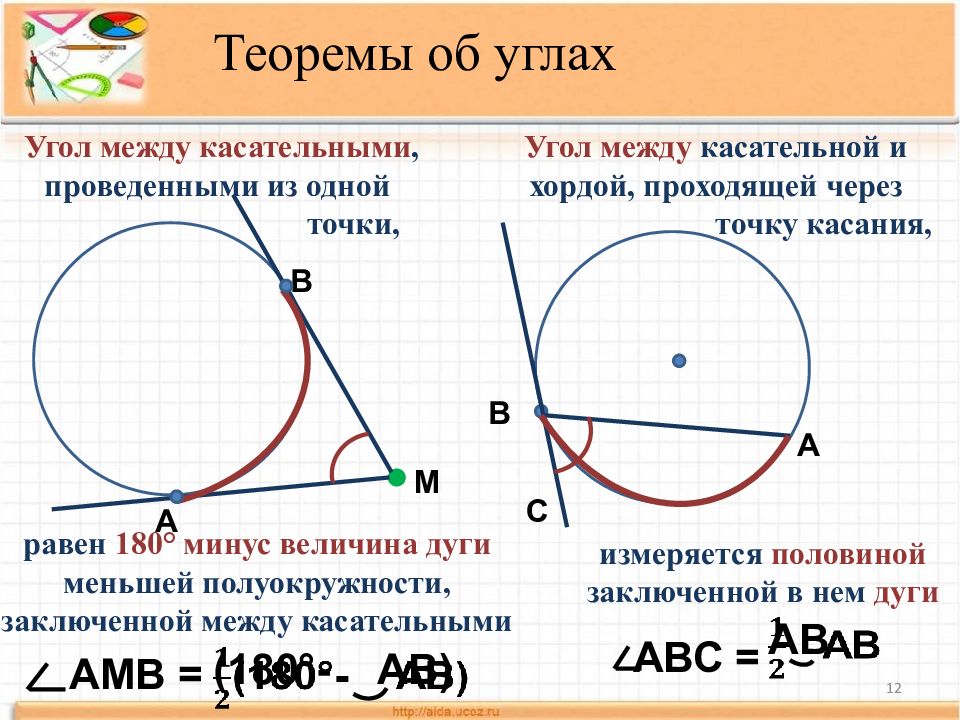
12 Теоремы об углах р авен 180° минус величина дуги меньшей полуокружности, заключенной между касательными А М В Угол между касательными, проведенными из одной точки, АМВ = (180°- АВ) Угол между касательной и хордой, проходящей через точку касания, измеряется половиной заключенной в нем дуги А В С АВС = АВ
Слайд 13
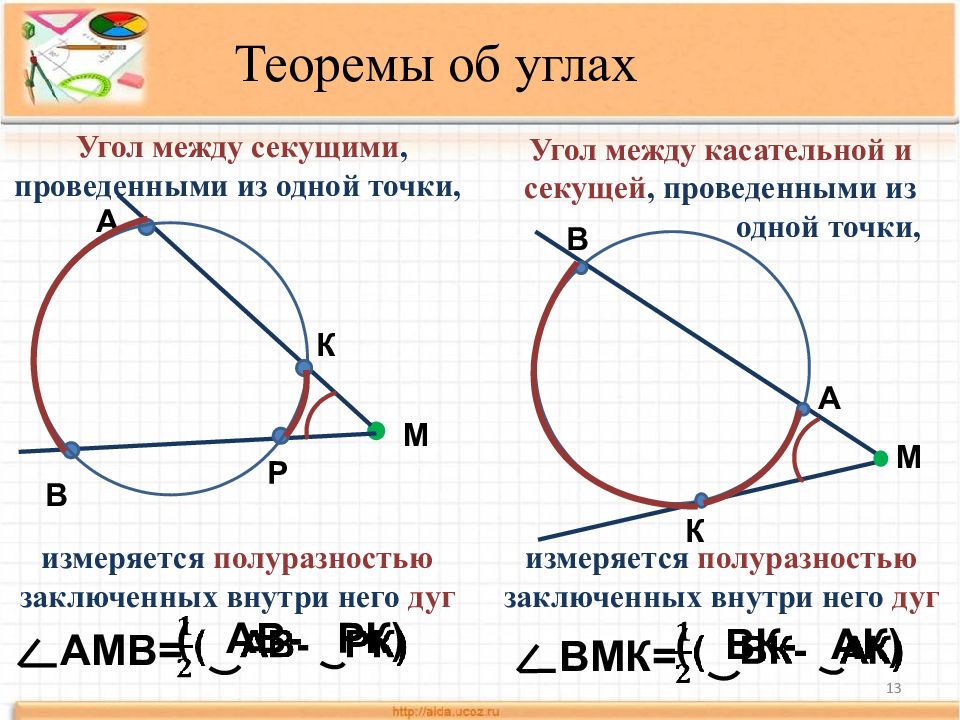
13 Теоремы об углах А М В К Угол между касательной и секущей, проведенными из одной точки, измеряется полуразностью заключенных внутри него дуг А В К М ( АВ- РК) АМВ= Угол между секущими, проведенными из одной точки, и змеряется полуразностью заключенных внутри него дуг Р ( ВК- АК) ВМК=
Слайд 14
14 Проверь себя… Вписанные углы, опирающиеся на одну и ту же дугу, равны. Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°. Если дуга окружности составляет 80°, то центральный угол, опирающийся на эту же дугу, равен 40°. Вписанные углы окружности равны. Если вписанный угол равен 30°, то центральный угол равен 60°. Вписанный угол в два раза меньше центрального угла. Вписанный угол, опирающийся на диаметр, прямой. Если вершины вписанных углов, опирающихся на одну хорду, лежат по одну сторону от данной хорды, то эти вписанные углы равны. Ответы Нет Д а Нет Нет Нет Нет Да Да
Слайд 15
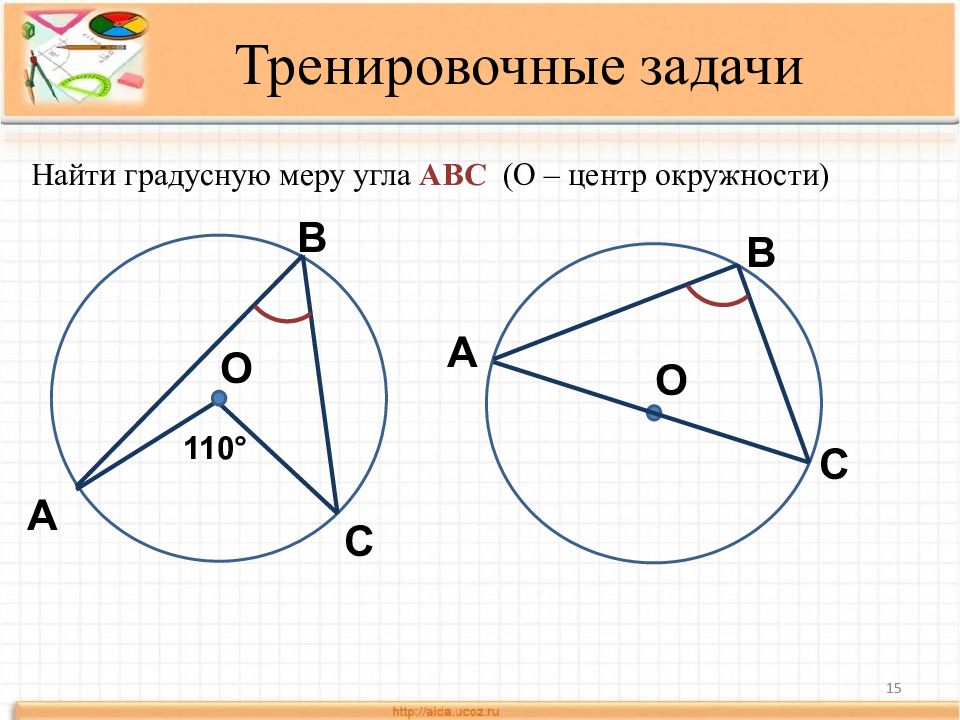
15 Тренировочные задачи В А С О Найти градусную меру угла АВС (О – центр окружности) 110° А В О С
Слайд 16
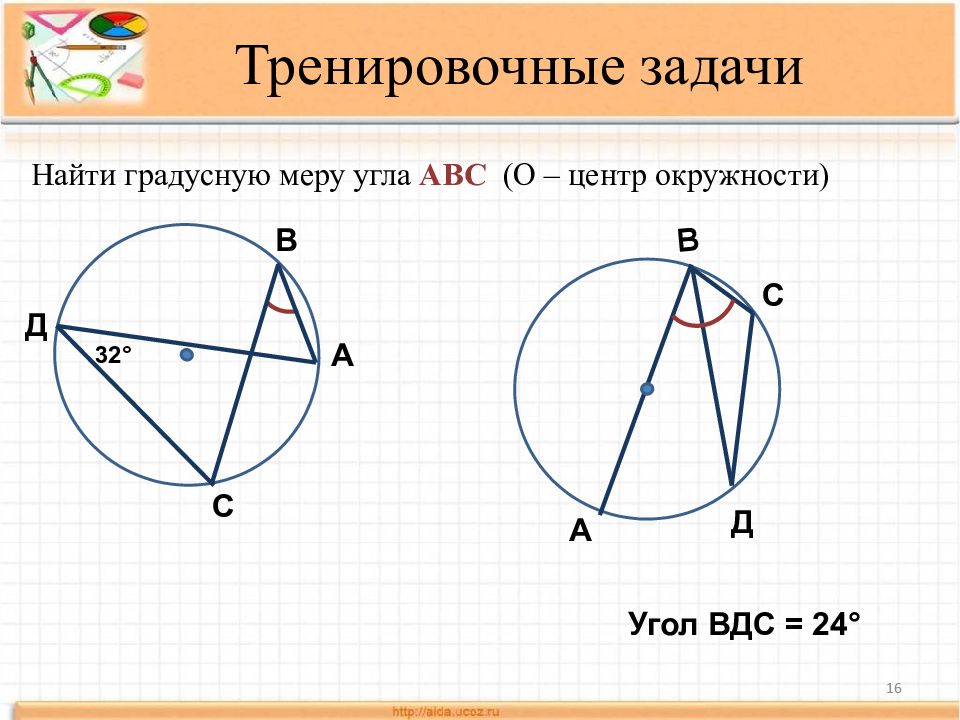
16 Тренировочные задачи Найти градусную меру угла АВС (О – центр окружности) 32° А В С Д А В С Д Угол ВДС = 24°
Слайд 17
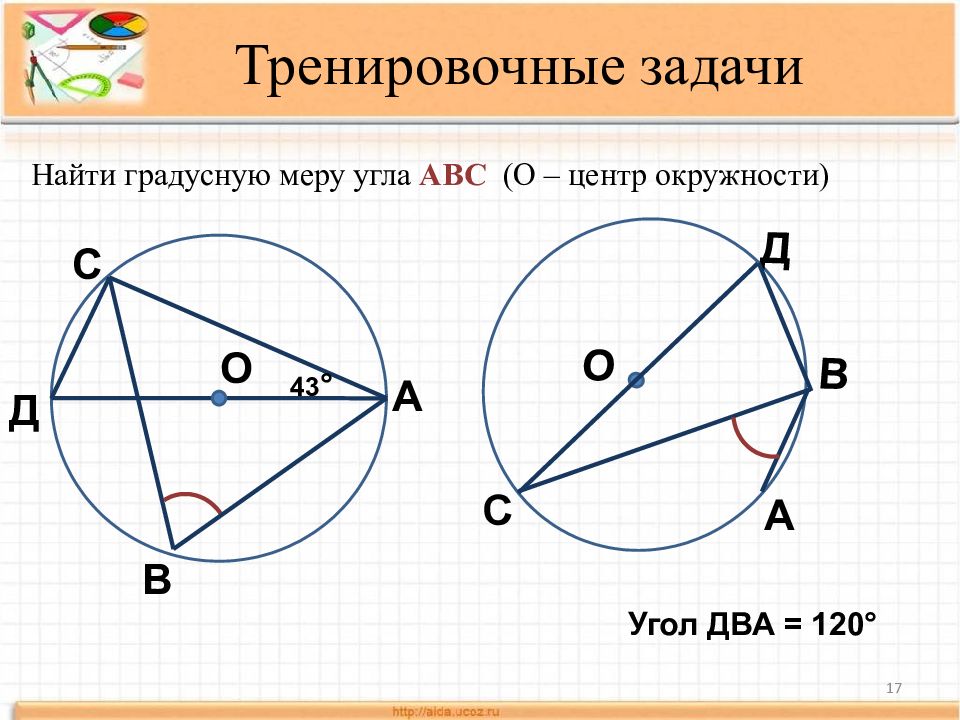
17 Тренировочные задачи В А С О Найти градусную меру угла АВС (О – центр окружности) 43 ° Д В О С Д А Угол ДВА = 120°
Слайд 18
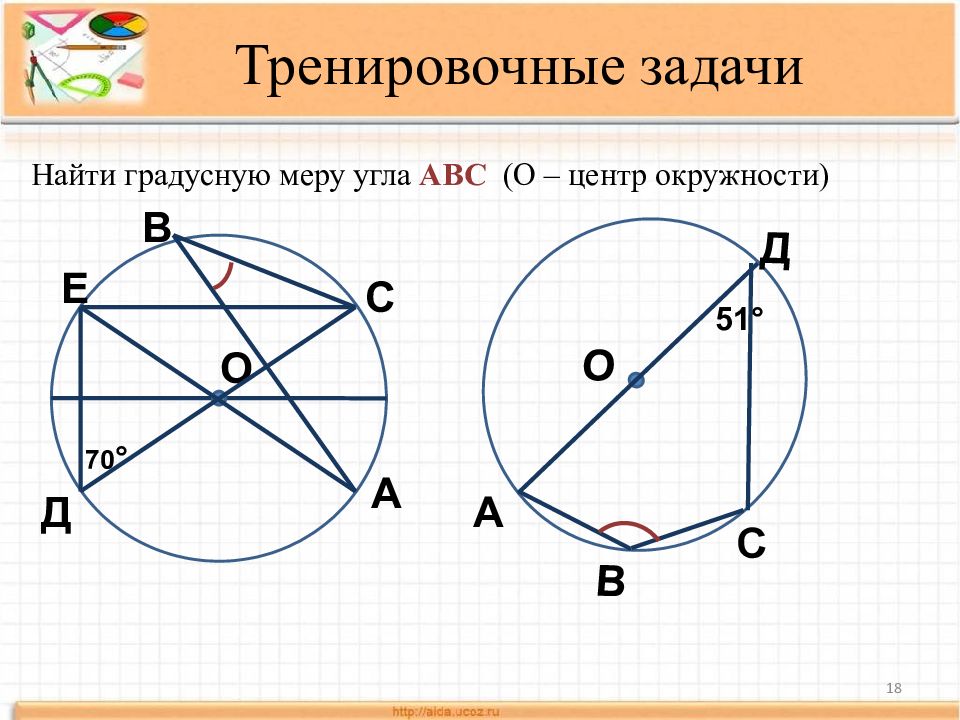
18 Тренировочные задачи А С Е О Найти градусную меру угла АВС (О – центр окружности) 70 ° Д В О С Д А 51° В
Слайд 20
20 Задача Угол между радиусом АО окружности, описанной около треугольника АВС и стороной АС равен 45°. Найдите угол А треугольника АВС, если угол С равен 25 °. Ответ: 110 ° ; 20 °
Слайд 21
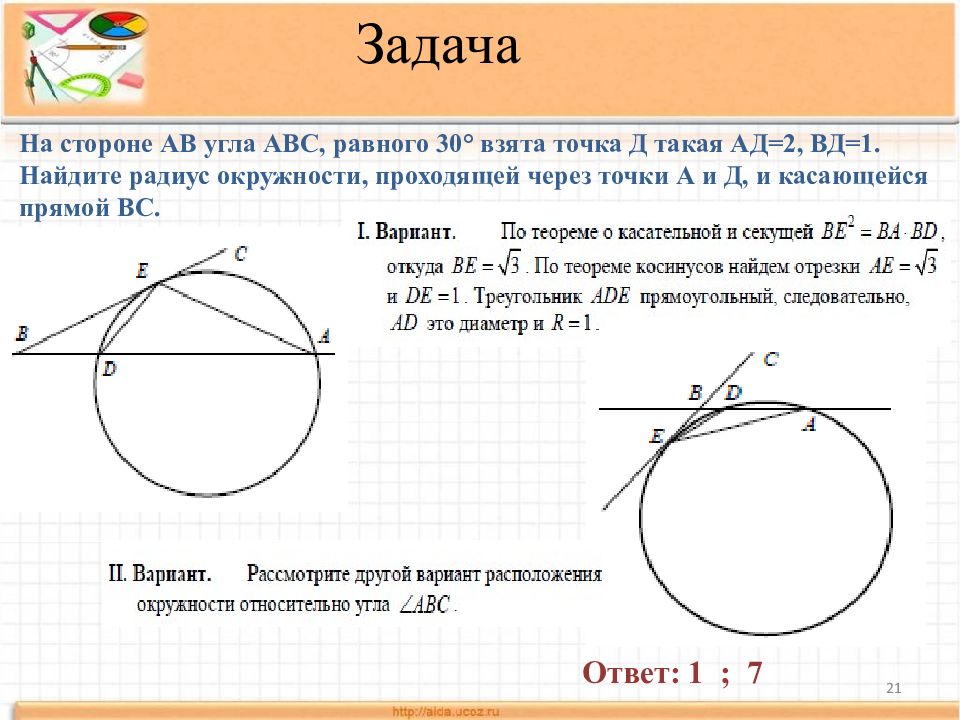
21 Задача На стороне АВ угла АВС, равного 30° взята точка Д такая АД=2, ВД=1. Найдите радиус окружности, проходящей через точки А и Д, и касающейся прямой ВС. Ответ: 1 ; 7
Слайд 22
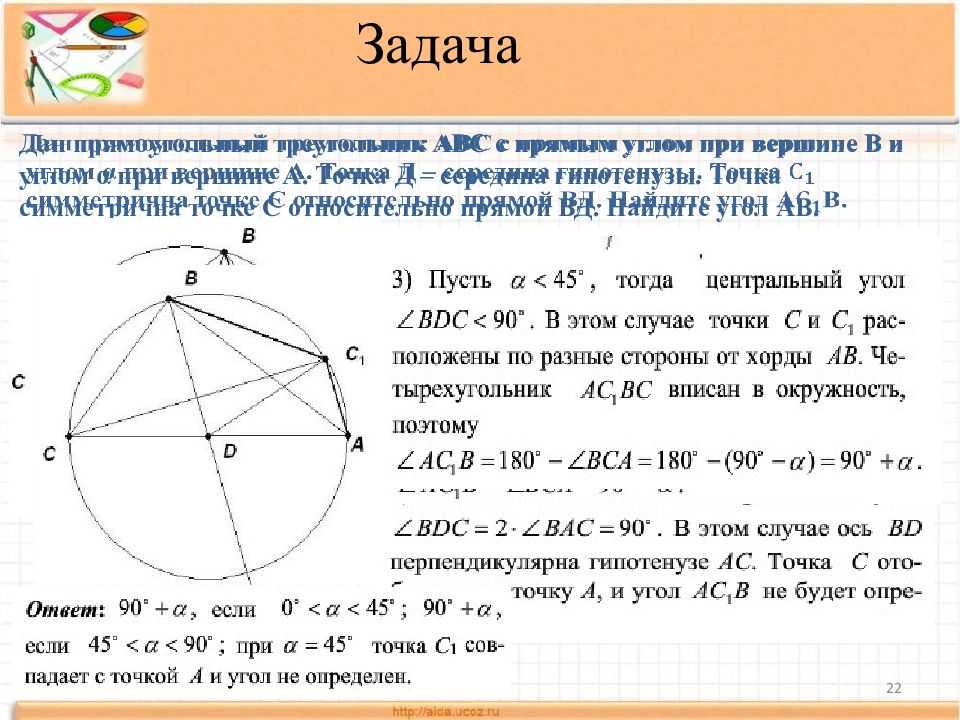
22 Задача Дан прямоугольный треугольник АВС с прямым углом при вершине В и углом α при вершине А. Точка Д – середина гипотенузы. Точка симметрична точке С относительно прямой ВД. Найдите угол А В.
Слайд 23
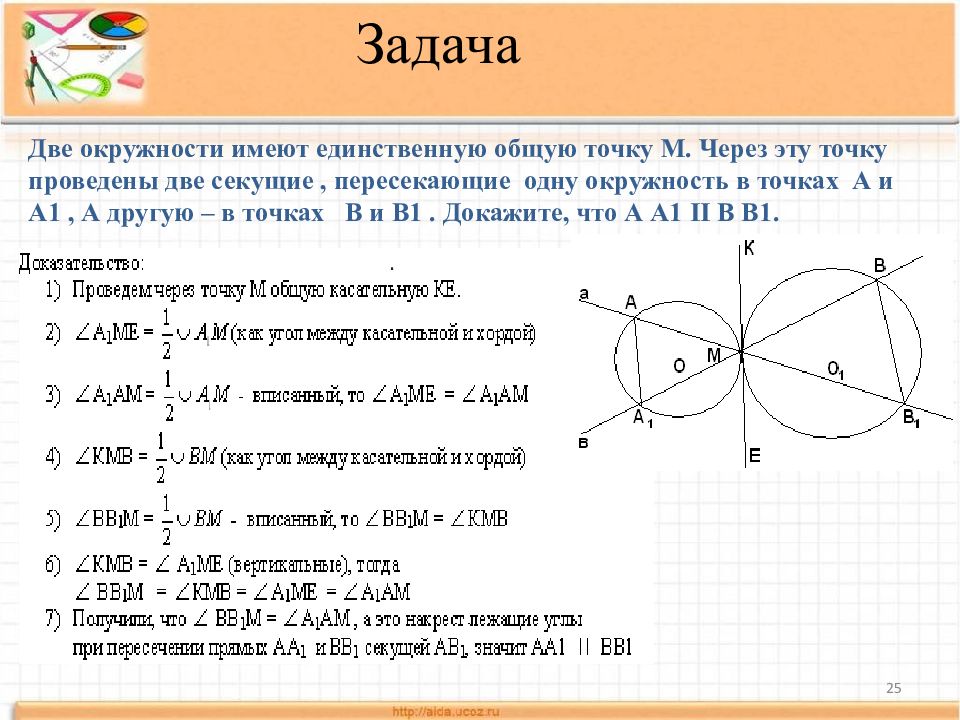
Пусть К – точка пересечения диагоналей вписанного в окружность четырехугольника АВСМ (АВ > СМ), угол МКС равен, а угол между прямыми АМ и ВС равен. Найти углы МВС и ВМА. Задача 23
Слайд 24
Окружность касается сторон АВ и АС треугольника АВС и пересекает сторону ВС в точках P и Q, BP=CQ. Докажите, что треугольник АВС равнобедренный. Задача 24