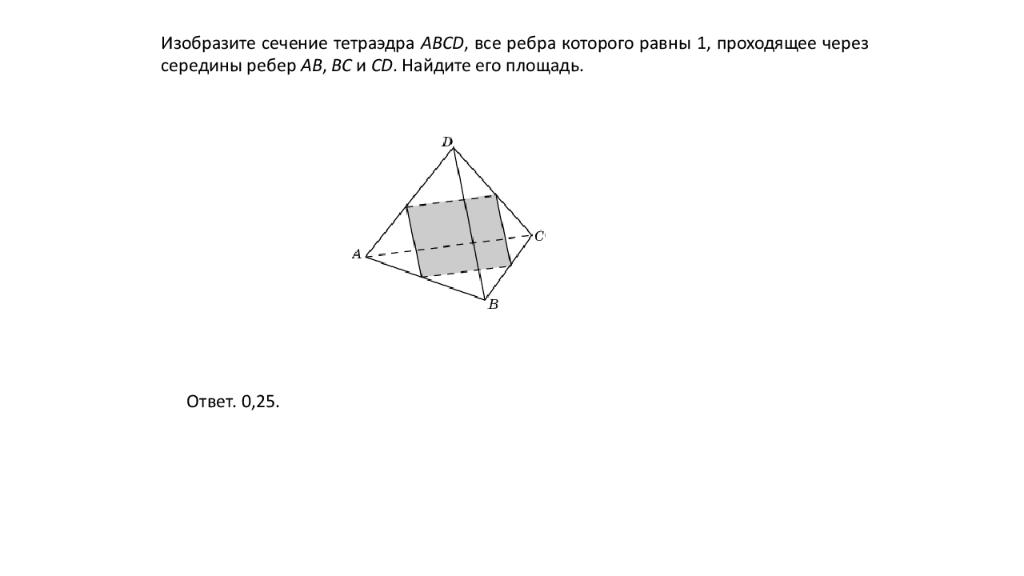
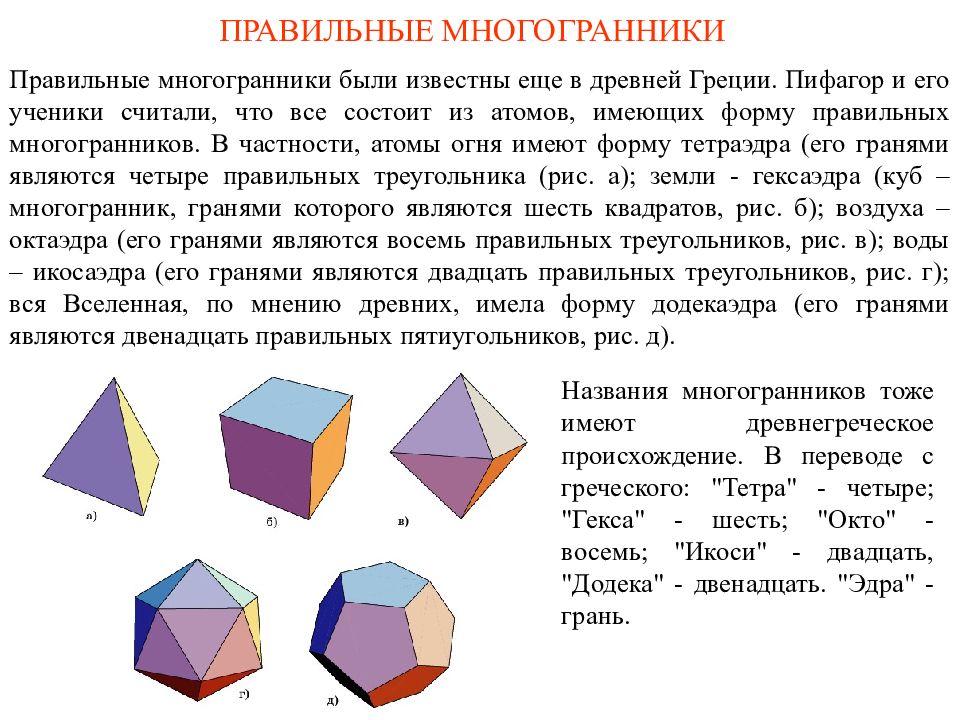
Первый слайд презентации
Изобразите сечение единичного куба A … D 1, проходящее через вершины A, B, C 1. Найдите его площадь. Ответ..
Слайд 2
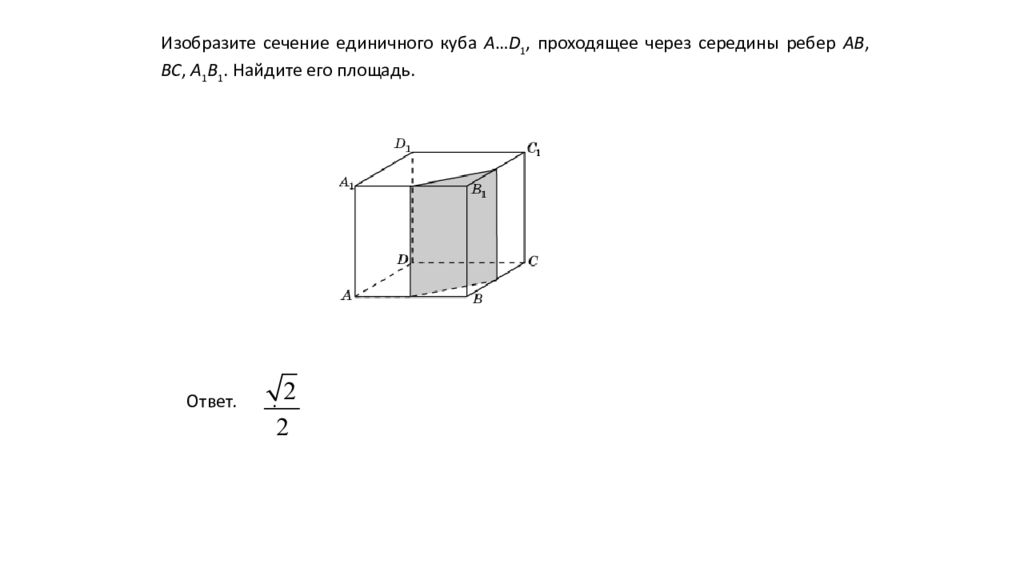
Изобразите сечение единичного куба A … D 1, проходящее через середины ребер AB, BC, A 1 B 1. Найдите его площадь. Ответ..
Слайд 3
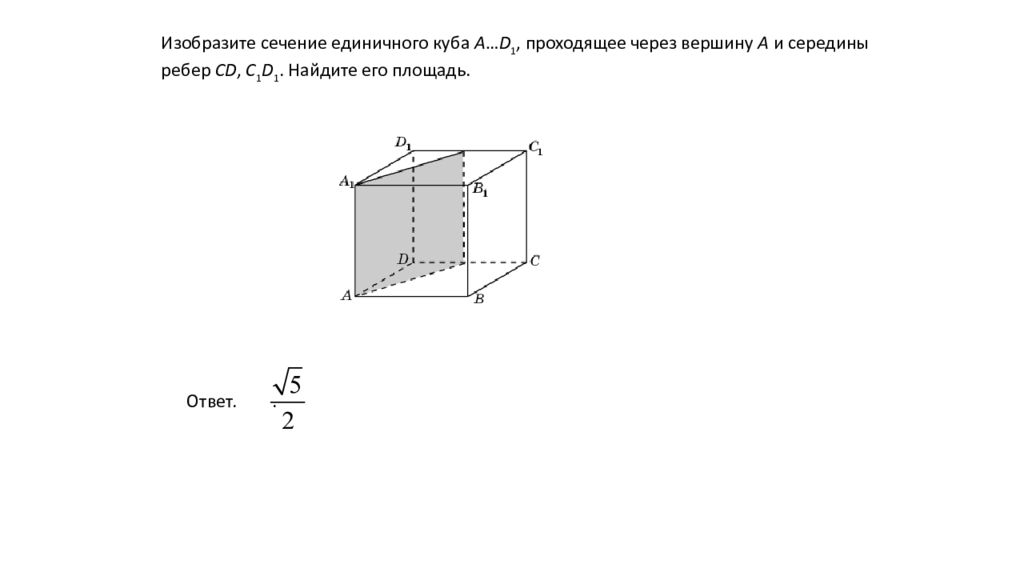
Изобразите сечение единичного куба A … D 1, проходящее через вершину A и середины ребер CD, C 1 D 1. Найдите его площадь. Ответ..
Слайд 4
Изобразите сечение единичного куба A … D 1, проходящее через вершину A и середины ребер BB 1, DD 1. Найдите его площадь. Ответ..
Слайд 5
Изобразите сечение единичного куба A … D 1, проходящее через вершины A, C и середину ребра С 1 D 1. Найдите его площадь. Решение. Сечением является равнобедренная трапеция ACEF. Ее основания AC и EF равны Высота FH равна Площадь сечения равна
Слайд 6
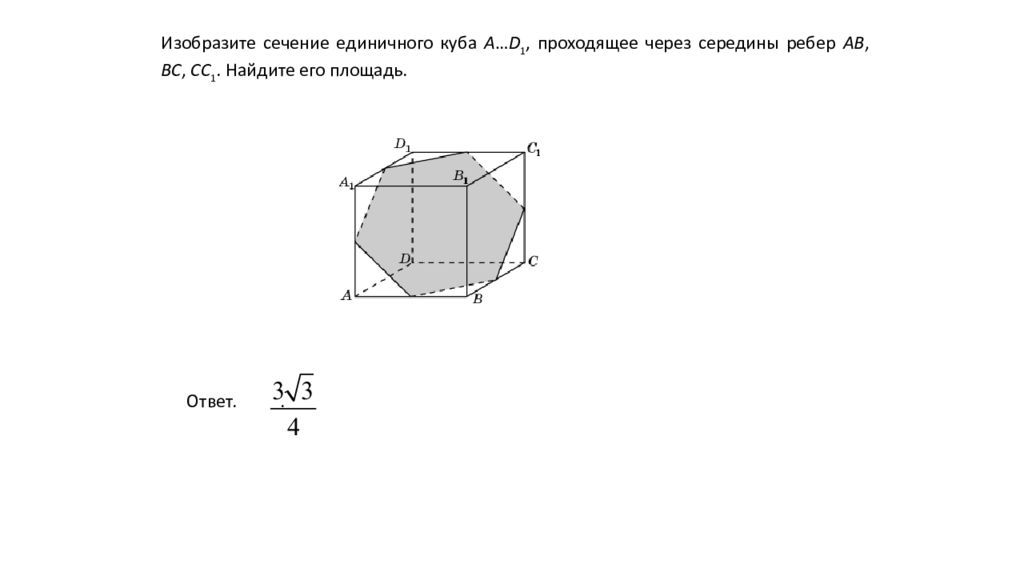
Изобразите сечение единичного куба A … D 1, проходящее через середины ребер AB, BC, CC 1. Найдите его площадь. Ответ..
Слайд 7
Изобразите сечение единичного куба A … D 1, проходящее через вершину A и середины ребер BC, DD 1. Найдите его площадь. Решение. Сечением является трапеция AEFG. Ее основания AG и EF равны соответственно и. Для нахождения ее высоты EH рассмотрим равнобедренный треугольник AEG, в котором AE = AG =, EG =. Высота, опущенная на сторону EG равна. Следовательно, высота EH равна. Площадь сечения равна.
Слайд 8
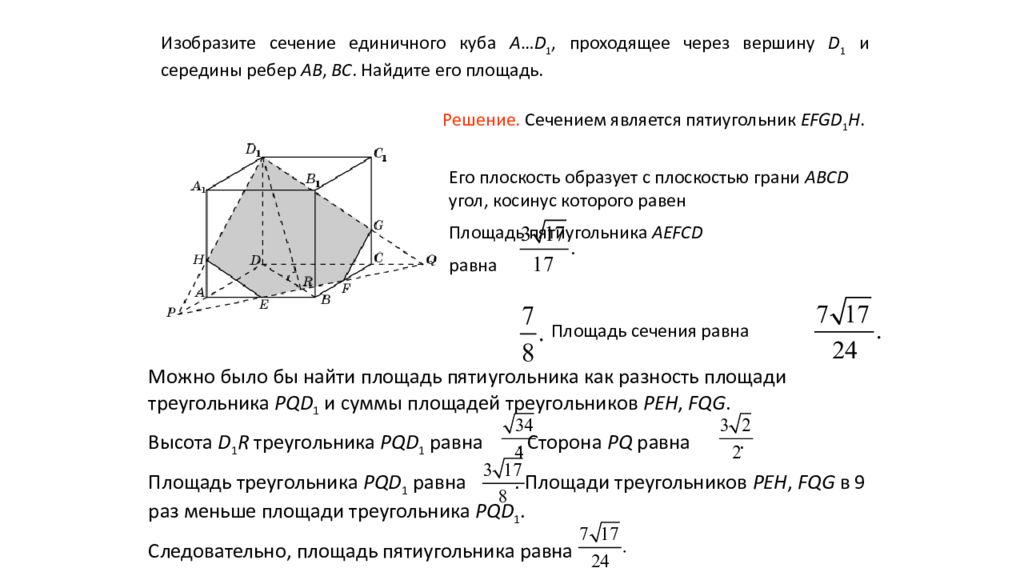
Изобразите сечение единичного куба A … D 1, проходящее через вершину D 1 и середины ребер AB, BC. Найдите его площадь. Решение. Сечением является пятиугольник EFGD 1 H. Площадь сечения равна Его плоскость образует с плоскостью грани ABCD угол, косинус которого равен Площадь пятиугольника AEFCD равна Можно было бы найти площадь пятиугольника как разность площади треугольника PQD 1 и суммы площадей треугольников PEH, FQG. Высота D 1 R треугольника PQD 1 равна. Сторона PQ равна. Площадь треугольника PQD 1 равна. Площади треугольников PEH, FQG в 9 раз меньше площади треугольника PQD 1. Следовательно, площадь пятиугольника равна