Слайд 2: Что такое пропорция ?
a : b или Если отношение a:b равно отношению c:d, то равенство a:b = c:d называют пропорцией. еще одна запись пропорции:
Слайд 3: Читаем правильно!
a:b = c:d « a так относится к b, как с относится к d » или «отношение a к b равно отношению c к d »
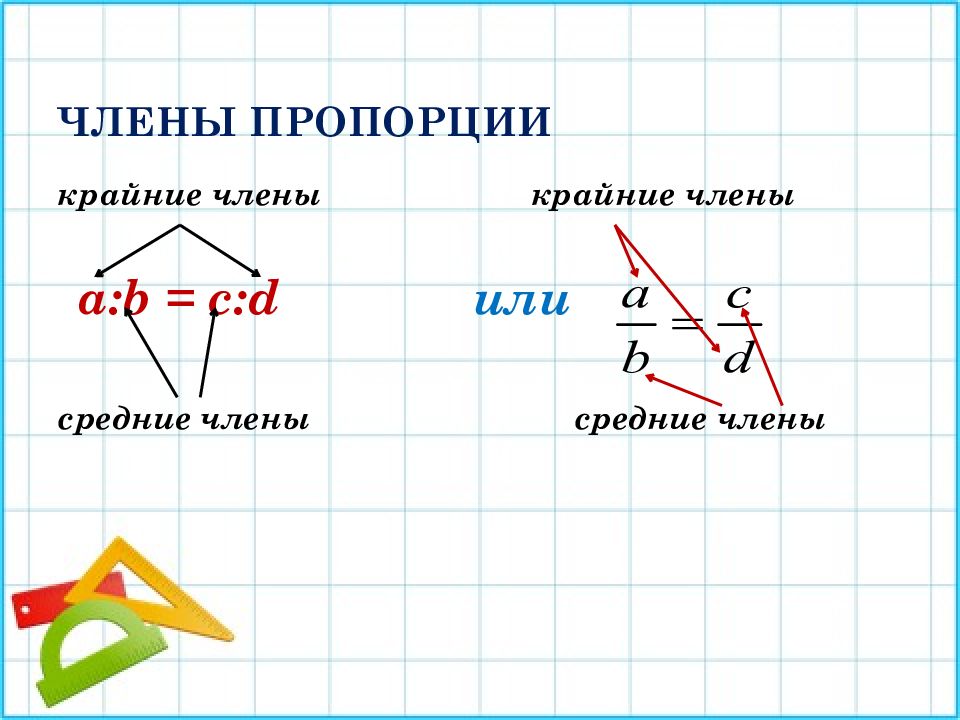
Слайд 4: Члены пропорции
крайние члены крайние члены a:b = c:d или средние члены средние члены
Слайд 5: Основное свойство пропорции
А как узнать, является ли пропорцией равенство ? Произведение крайних членов пропорции равно произведению её средних членов если, то ad = bc Проверим: - пропорция Аналогично: №144
Слайд 6: Основное свойство пропорции
Произведение крайних членов пропорции равно произведению её средних членов если, то ad = bc Определи, какое из равенств является пропорцией:
Пример 1. Найдем неизвестный член пропорции 5:40 = 7: x Аналогично: № 145
Слайд 8
Пропорция. Решение задач на прямую пропорциональность №151(а) Условие: дождь шел 2.5 часа и выпало 1,5 мм осадков. Сколько осадков выпало бы за 6 часов, если бы дождь шел с такой же силой Решение: Чем больше время, тем больше осадков. Величины прямопропорциональны. Составим пропорцию, обозначив неизвестное за Х 2,5ч----------------- 1,5 мм 6 ч ----------------- Х мм 2,5 : 6= 1,5 : Х Найдем Х: Х= (1,5 * 6) / 2,5 = 3,6 Ответ: 3,6 мм
Слайд 9
Пропорция. Решение задач на обратную пропорциональность №154 (А) Условие: 9 рабочих могут выполнить работу за 10 часов. Сколько нужно рабочих, чтобы выполнить эту работу за 6 часов Решение: Чем больше рабочих, тем меньше время. Величины обратнопропорциональны. Составим пропорцию, обозначив неизвестное за Х 10 ч----------------- 9 раб. 6 ч ----------------- Х раб 10 Х 6 9 Найдем Х: Х= (10 * 9) / 6 = 15 Ответ: 15