Первый слайд презентации
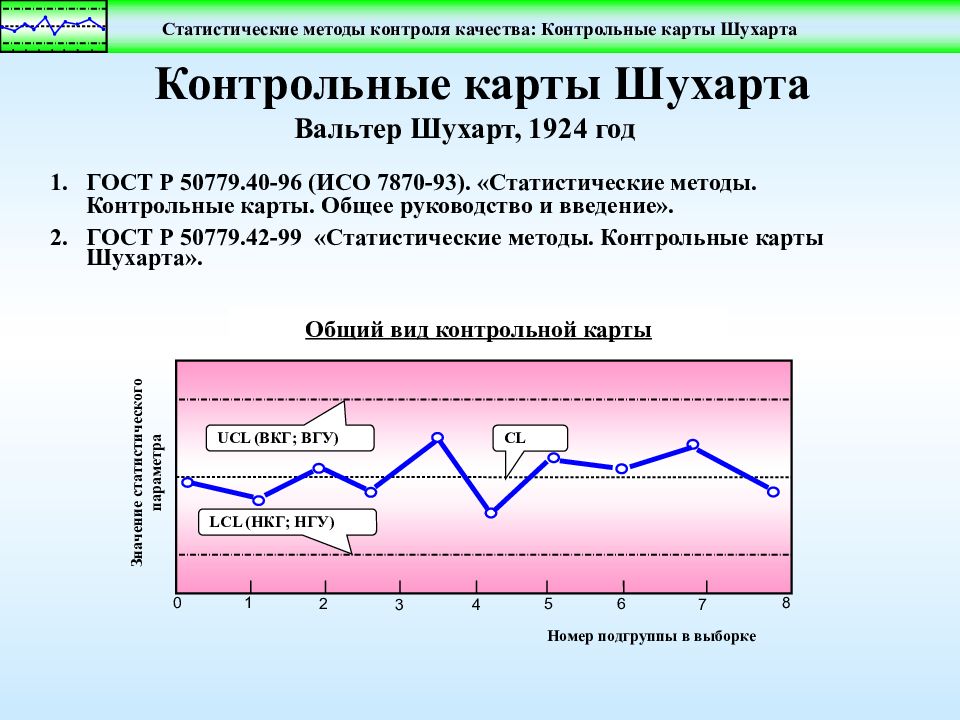
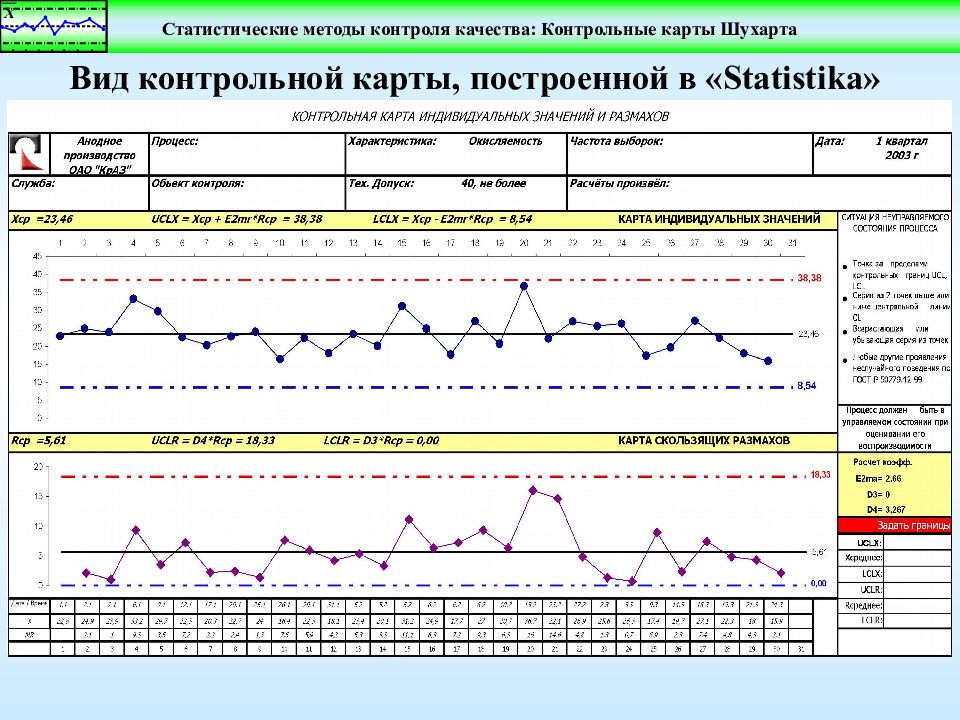
Контрольные карты Шухарта ГОСТ Р 50779.40-96 (ИСО 7870-93). «Статистические методы. Контрольные карты. Общее руководство и введение». ГОСТ Р 50779.42-99 «Статистические методы. Контрольные карты Шухарта». Вальтер Шухарт, 1924 год Общий вид контрольной карты Значение статистического параметра Номер подгруппы в выборке LCL ( НКГ; НГУ ) UCL ( ВКГ; ВГУ ) CL 0 1 2 3 4 5 6 7 8
Слайд 2
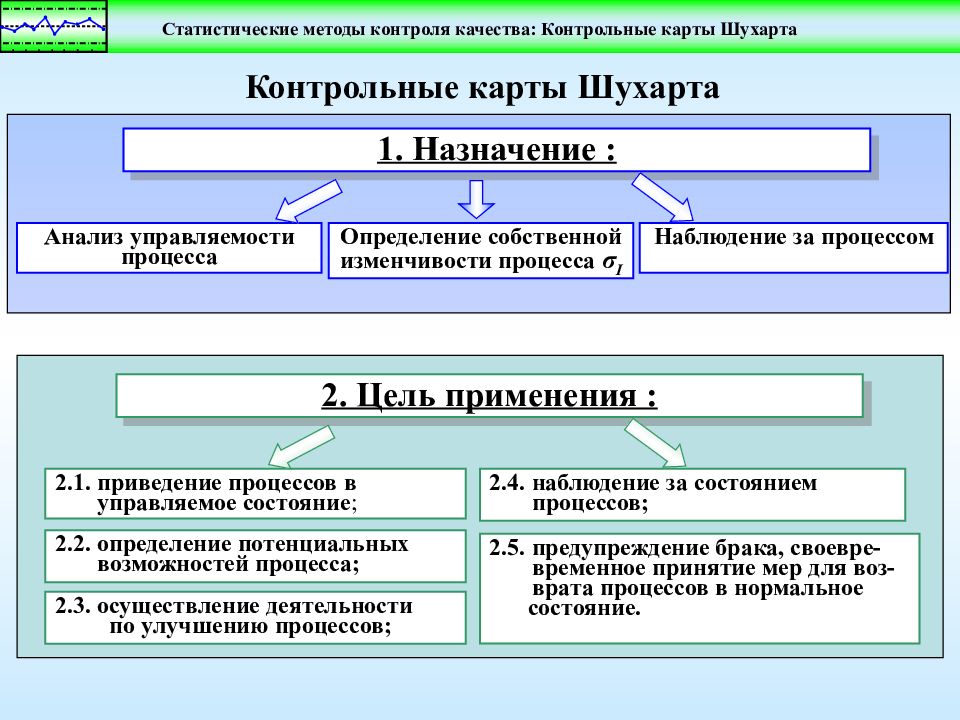
Контрольные карты Шухарта 2.1. приведение процессов в управляемое состояние ; 2. Цель применения : 2.2. определение потенциальных возможностей процесса; 2.4. наблюдение за состоянием процессов; 2.5. предупреждение брака, своевре- временное принятие мер для воз- врата процессов в нормальное состояние. 2.3. осуществление деятельности по улучшению процессов; Наблюдение за процессом Анализ управляемости процесса 1. Назначение : Определение собственной изменчивости процесса σ I
Слайд 3
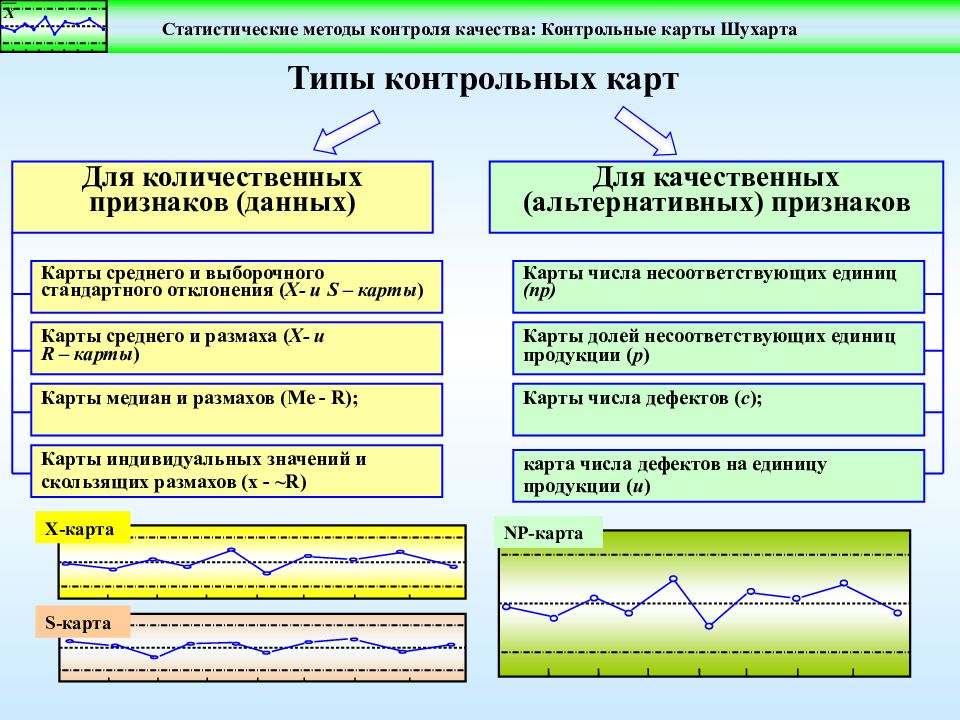
Типы контрольных карт Для количественных признаков (данных) Карты среднего и выборочного стандартного отклонения ( Х- и S – карты ) Карты среднего и размаха ( Х- и R – карты ) Карты индивидуальных значений и скользящих размахов (x - ~R) Карты медиан и размахов (Me - R ); Для качественных (альтернативных) признаков Карты числа несоответствующих единиц ( np) Карты долей несоответствующих единиц продукции ( p ) Карты числа дефектов ( с ); карта числа дефектов на единицу продукции ( u ) Х-карта S -карта NP -карта
Слайд 4
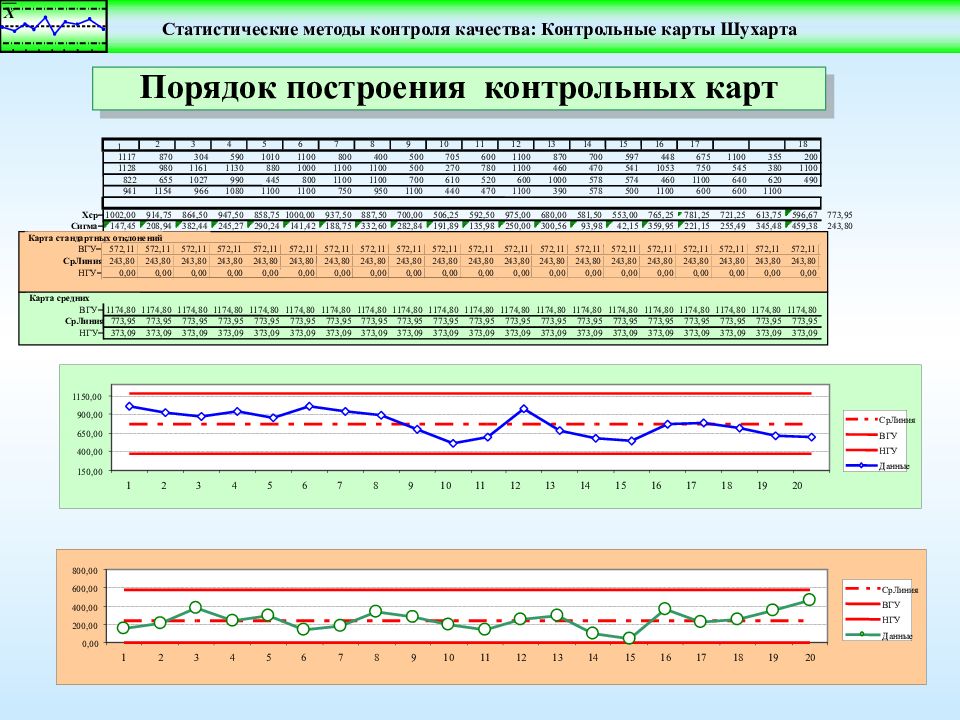
Порядок построения контрольных карт 1. Собрать данные в порядке возрастания по времени при неизменных условиях ведения процесса; 2. Объединить данные в подгруппы с количеством данных 2-20; 3. Для каждой подгруппы вычислить Хср и ; 4. Вычислить «Среднее средних» -это будет центральная линия на карте средних значений; 5. Вычислить ср -это будет центральная линия на карте стандартных отклонений; 6. Вычислить границы управления для контрольной карты средних значений и контрольной кар ты стандартных отклонений и нанести их на соответствующие карты; 7. Нанести на контрольную карту средних значений значения групповых средних ; 8. Нанести на контрольную карту стандартных отклонений значения групповых стандартных отклонений ;
Слайд 7
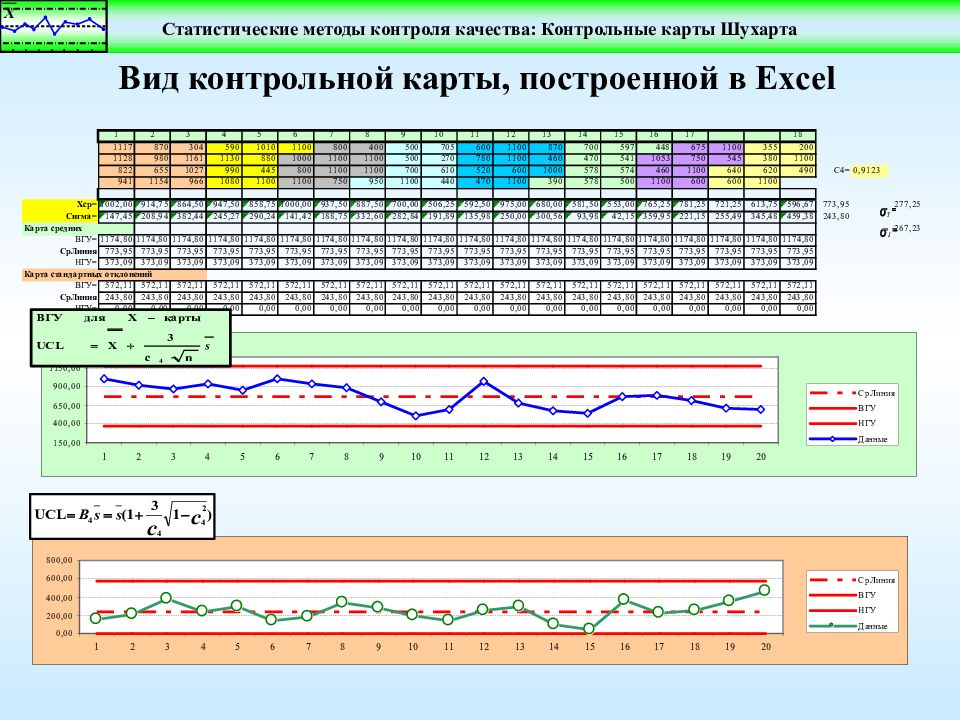
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1117 870 304 590 1010 1100 800 400 500 705 600 1100 870 700 597 448 675 1100 355 200 1128 980 1161 1130 880 1000 1100 1100 500 270 780 1100 460 470 541 1053 750 545 380 1100 822 655 1027 990 445 800 1100 1100 700 610 520 600 1000 578 574 460 1100 640 620 490 941 1154 966 1080 1100 1100 750 950 1100 440 470 1100 390 578 500 1100 600 600 1100 773,95 243,80 Сигма= 147,45 208,94 382,44 245,27 290,24 141,42 188,75 332,60 282,84 191,89 135,98 250,00 300,56 93,98 42,15 359,95 221,15 255,49 345,48 459,38 Хср= 1002,00 914,75 864,50 947,50 858,75 1000,00 937,50 887,50 700,00 506,25 592,50 975,00 680,00 581,50 553,00 765,25 781,25 721,25 613,75 596,67 Карта средних ВГУ= 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 1174,80 СрЛиния 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 773,95 НГУ= 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 373,09 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 150,00 400,00 650,00 900,00 1150,00 СрЛиния ВГУ НГУ Данные ВГУ= 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 572,11 СрЛиния 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 243,80 НГУ= 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 Карта стандартных отклонений 0,00 200,00 400,00 600,00 800,00 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 СрЛиния ВГУ НГУ Данные Порядок построения контрольных карт
Слайд 8
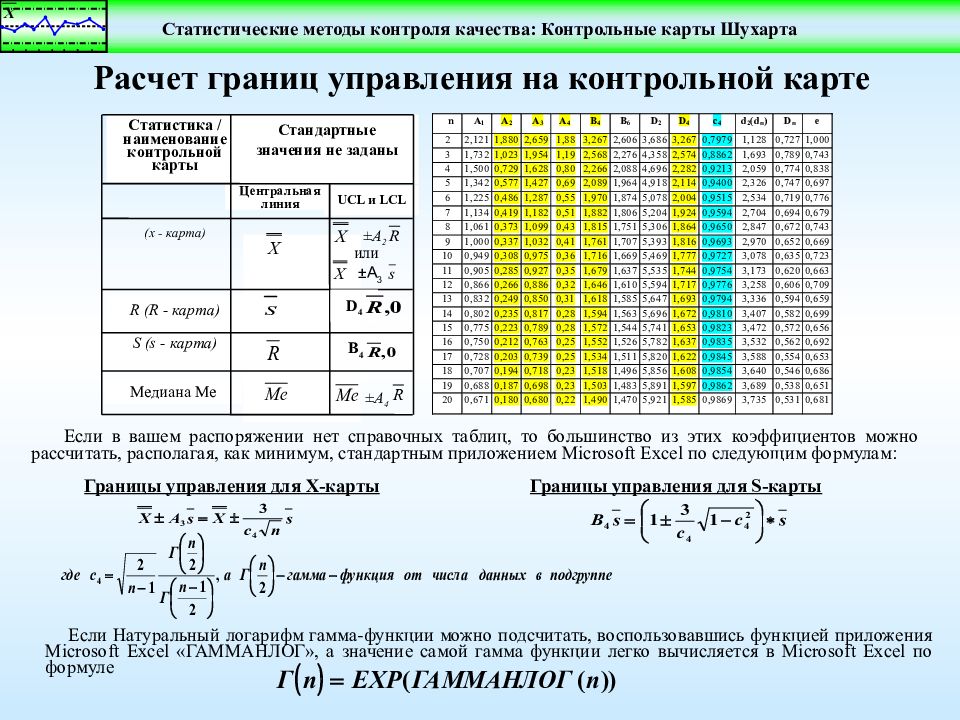
Если в вашем распоряжении нет справочных таблиц, то большинство из этих коэффициентов можно рассчитать, располагая, как минимум, стандартным приложением Microsoft Excel по следующим формулам: Медиана Me S ( s - карта) R ( R - карта) UCL и LCL Центральная линия Стандартные значения не заданы Статистика / наименование контрольной карты ±A 2 ±A 3 или B 4 D 4 ±A 4 (х - карта) Расчет границ управления на контрольной карте Границы управления для Х-карты Границы управления для S -карты Если Натуральный логарифм гамма-функции можно подсчитать, воспользовавшись функцией приложения Microsoft Excel «ГАММАНЛОГ», а значение самой гамма функции легко вычисляется в Microsoft Excel по формуле
Слайд 9
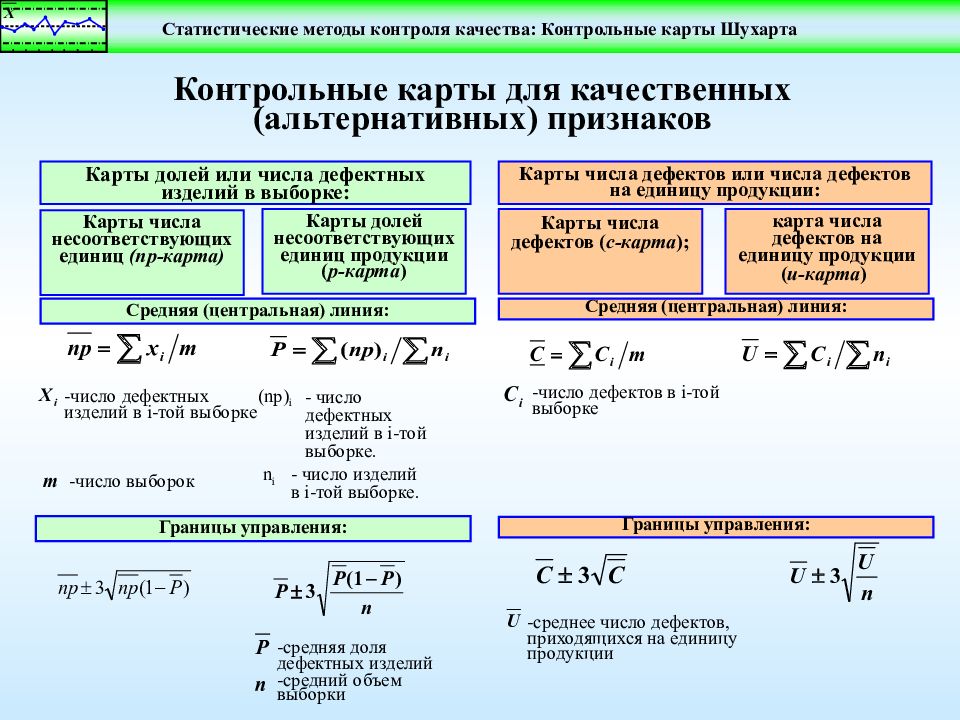
Карты долей или числа дефектных изделий в выборке: Карты числа дефектов или числа дефектов на единицу продукции: Контрольные карты для качественных (альтернативных) признаков Границы управления: Средняя (центральная) линия: Карты числа несоответствующих единиц ( np -карта ) -число дефектных изделий в i- той выборке -число выборок Карты долей несоответствующих единиц продукции ( p -карта ) - число дефектных изделий в i -той выборке. - число изделий в i- той выборке. n i -средняя доля дефектных изделий -средний объем выборки (np) i Границы управления: карта числа дефектов на единицу продукции ( u -карта ) Карты числа дефектов ( с-карта ); -число дефектов в i- той выборке -среднее число дефектов, приходящихся на единицу продукции Средняя (центральная) линия:
Слайд 10
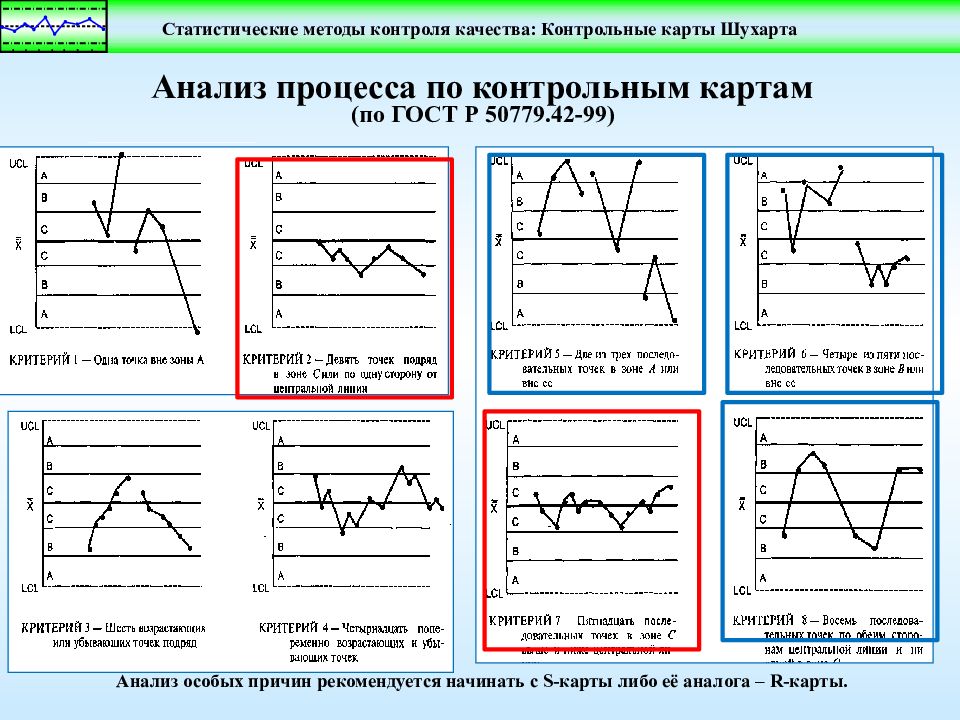
Анализ процесса по контрольным картам (по ГОСТ Р 50779.42-99) Анализ особых причин рекомендуется начинать с S- карты либо её аналога – R -карты.
Слайд 11
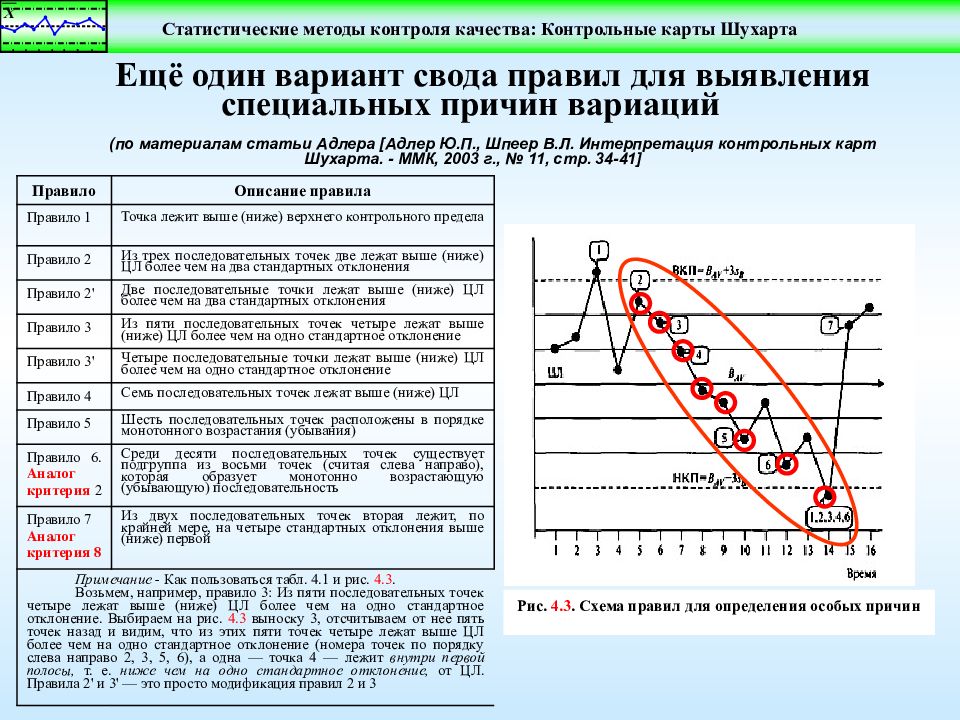
Правило Описание правила Правило 1 Точка лежит выше (ниже) верхнего контрольного предела Правило 2 Из трех последовательных точек две лежат выше (ниже) ЦЛ более чем на два стандартных отклонения Правило 2' Две последовательные точки лежат выше (ниже) ЦЛ более чем на два стандартных отклонения Правило 3 Из пяти последовательных точек четыре лежат выше (ниже) ЦЛ более чем на одно стандартное отклонение Правило 3' Четыре последовательные точки лежат выше (ниже) ЦЛ более чем на одно стандартное отклонение Правило 4 Семь последовательных точек лежат выше (ниже) ЦЛ Правило 5 Шесть последовательных точек расположены в порядке монотонного возрастания (убывания) Правило 6. Аналог критерия 2 Среди десяти последовательных точек существует подгруппа из восьми точек (считая слева направо), которая образует монотонно возрастающую (убывающую) последовательность Правило 7 Аналог критерия 8 Из двух последовательных точек вторая лежит, по крайней мере, на четыре стандартных отклонения выше (ниже) первой Примечание - Как пользоваться табл. 4.1 и рис. 4.3. Возьмем, например, правило 3: Из пяти последовательных точек четыре лежат выше (ниже) ЦЛ более чем на одно стандартное отклонение. Выбираем на рис. 4.3 выноску 3, отсчитываем от нее пять точек назад и видим, что из этих пяти точек четыре лежат выше ЦЛ более чем на одно стандартное отклонение (номера точек по порядку слева направо 2, 3, 5, 6), а одна — точка 4 — лежит внутри первой полосы, т. е. ниже чем на одно стандартное отклонение, от ЦЛ. Правила 2' и 3' — это просто модификация правил 2 и 3 Ещё один вариант свода п равил для выявления специальных причин вариаций (по материалам статьи Адлера [Адлер Ю.П., Шпеер В.Л. Интерпретация контрольных карт Шухарта. - ММК, 2003 г., № 11, стр. 34-41] Рис. 4.3. Схема правил для определения особых причин
Слайд 12
Действия при выявлении на контрольной карте признака неуправляемого состояния процесса Определить период времени, когда были получены данные, входящие в подгруппу (или подгруппы), в которой проявился признак неуправляемости процесса. 1. Дать задание «владельцу процесса» выяснить и устранить причину неуправляемого состояния процесса в определенный по п.1 период времени. 2. Исключить из исходных данных подгруппы, в которых проявился признак неуправляемого состояния процесса. 3. Пересчитать центральную линию, границы управления и вновь построить контрольную карту. 4. Проанализировать вновь построенную карту на наличие признаков неуправляемого состояния процесса. 5. В случае выявления на вновь построенной карте признаков неуправляемого состояния процесса повторить п.п. 1-5. 6. Повторять п.п. 1-7 до тех пор, пока не будет получена карта без признаков неуправляемого состояния процесса. 7. 8. Вычислить собственную изменчивость процесса σ I (собственное стандартное отклонение процесса или стандартное отклонение процесса без учета его неуправляемых периодов). и собственное среднее значение процесса. Вычислить показатели Ср и Срк потенциальных возможностей процесса используя при их расчете в качестве стандартного отклонения собственную изменчивость процесса σ I и собственное среднее значение процесса. 9.
Слайд 13
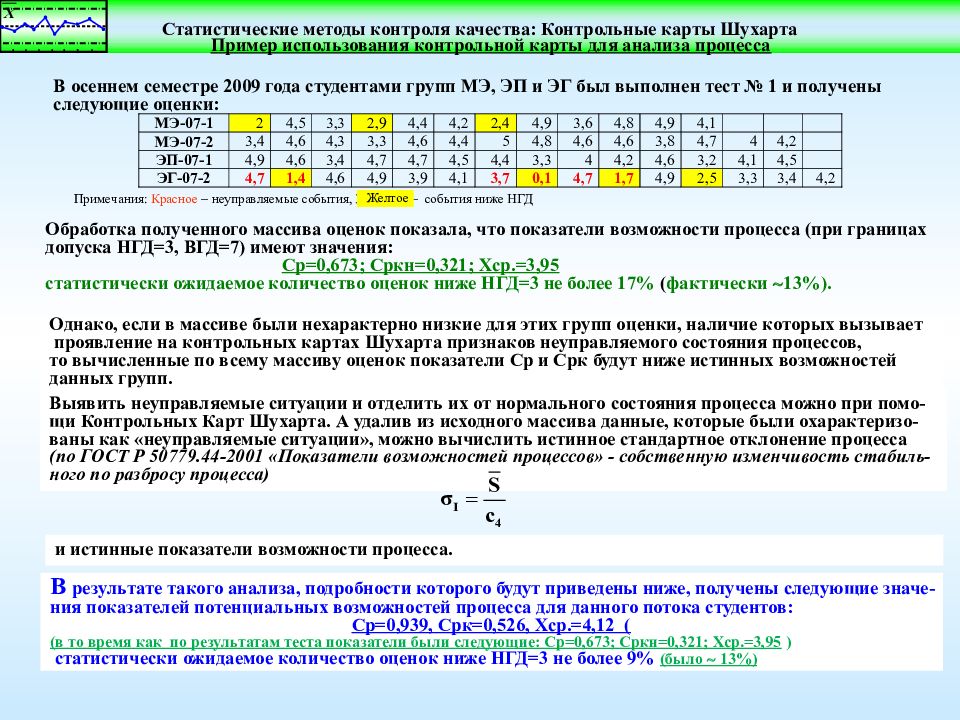
Пример использования контрольной карты для анализа процесса В осеннем семестре 2009 года студентами групп МЭ, ЭП и ЭГ был выполнен тест № 1 и получены следующие оценки: Обработка полученного массива оценок показала, что показатели возможности процесса (при границах допуска НГД=3, ВГД=7) имеют значения: Ср=0,673; Сркн=0,321; Хср.=3,95 статистически ожидаемое количество оценок ниже НГД=3 не более 17% ( фактически 13% ). Однако, если в массиве были нехарактерно низкие для этих групп оценки, наличие которых вызывает проявление на контрольных картах Шухарта признаков неуправляемого состояния процессов, то вычисленные по всему массиву оценок показатели Ср и Срк будут ниже истинных возможностей данных групп. В результате такого анализа, подробности которого будут приведены ниже, получены следующие значе- ния показателей потенциальных возможностей процесса для данного потока студентов: Ср=0,939, Срк=0,526, Хср.=4,12 ( (в то время как по результатам теста показатели были следующие: Ср=0,673; Сркн=0,321; Хср.=3,95 ) статистически ожидаемое количество оценок ниже НГД=3 не более 9% (было 13%) Выявить неуправляемые ситуации и отделить их от нормального состояния процесса можно при помо- щи Контрольных Карт Шухарта. А удалив из исходного массива данные, которые были охарактеризо- ваны как «неуправляемые ситуации», можно вычислить истинное стандартное отклонение процесса (по ГОСТ Р 50779.44-2001 «Показатели возможностей процессов» - собственную изменчивость стабиль- ного по разбросу процесса) и истинные показатели возможности процесса. Примечания: Красное – неуправляемые события, Желтое – события ниже НГД Желтое
Слайд 14
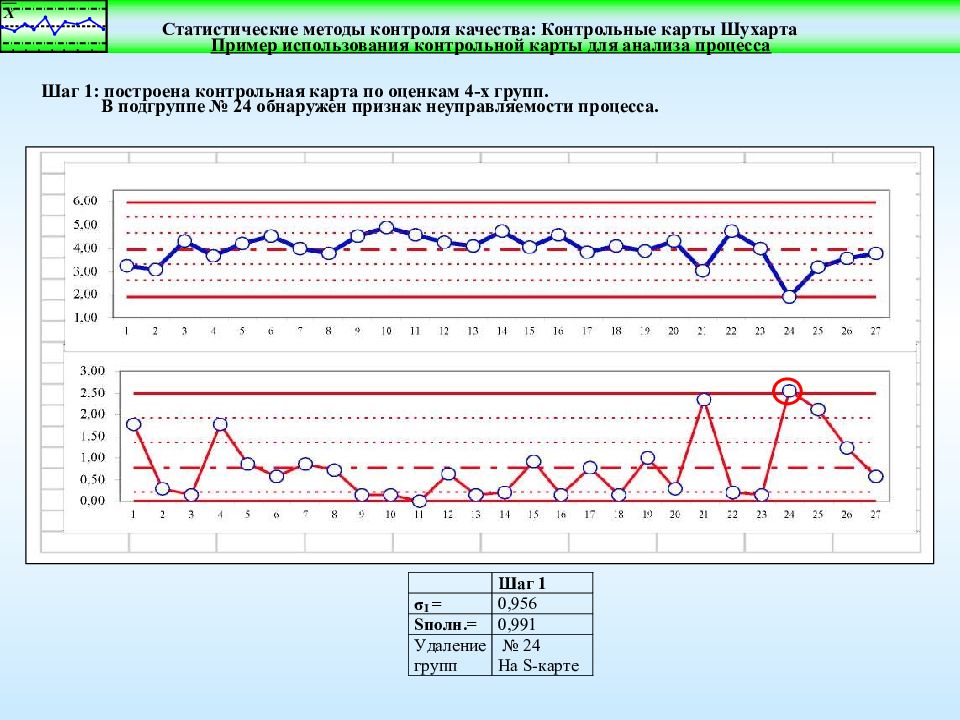
Пример использования контрольной карты для анализа процесса Шаг 1: построена контрольная карта по оценкам 4-х групп. В подгруппе № 24 обнаружен признак неуправляемости процесса.
Слайд 15
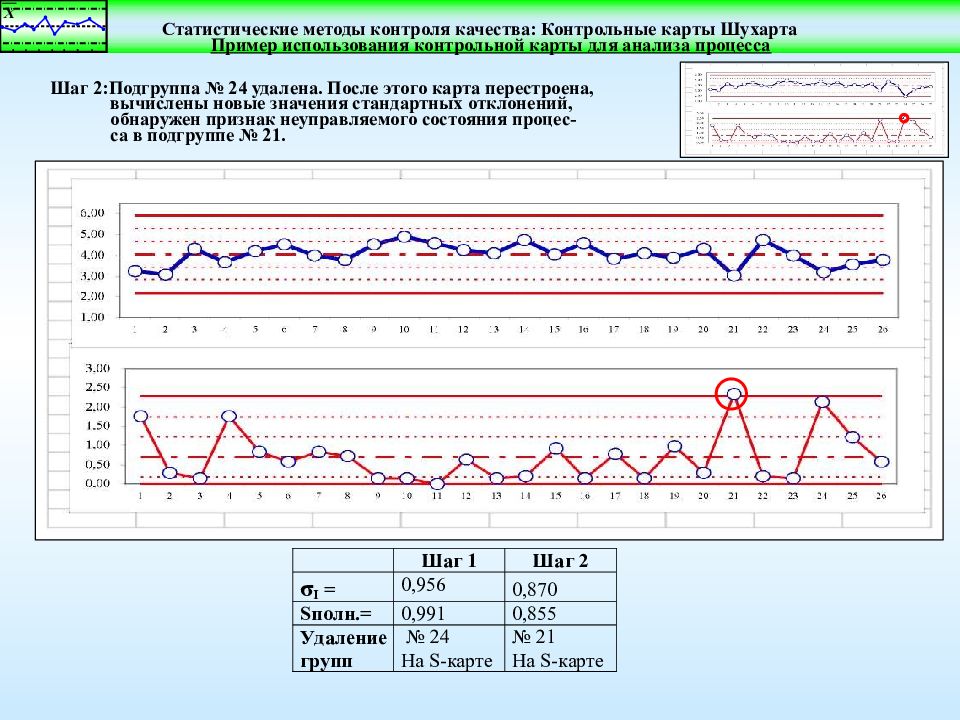
Пример использования контрольной карты для анализа процесса Шаг 2:Подгруппа № 24 удалена. После этого карта перестроена, вычислены новые значения стандартных отклонений, обнаружен признак неуправляемого состояния процес- са в подгруппе № 21.
Слайд 16
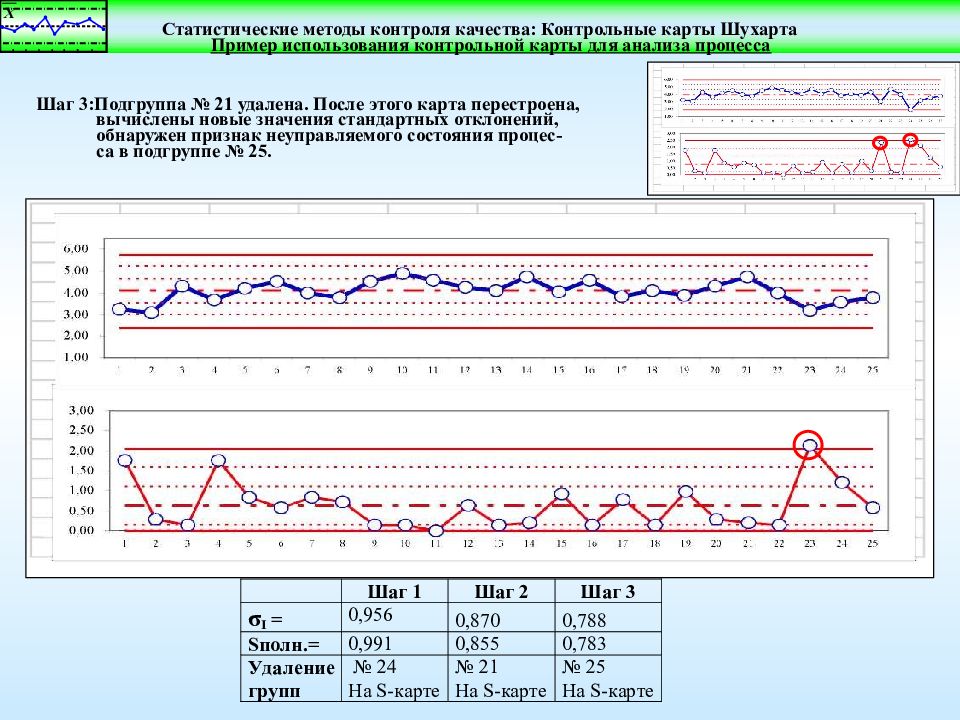
Пример использования контрольной карты для анализа процесса Шаг 3:Подгруппа № 21 удалена. После этого карта перестроена, вычислены новые значения стандартных отклонений, обнаружен признак неуправляемого состояния процес- са в подгруппе № 25.
Слайд 17
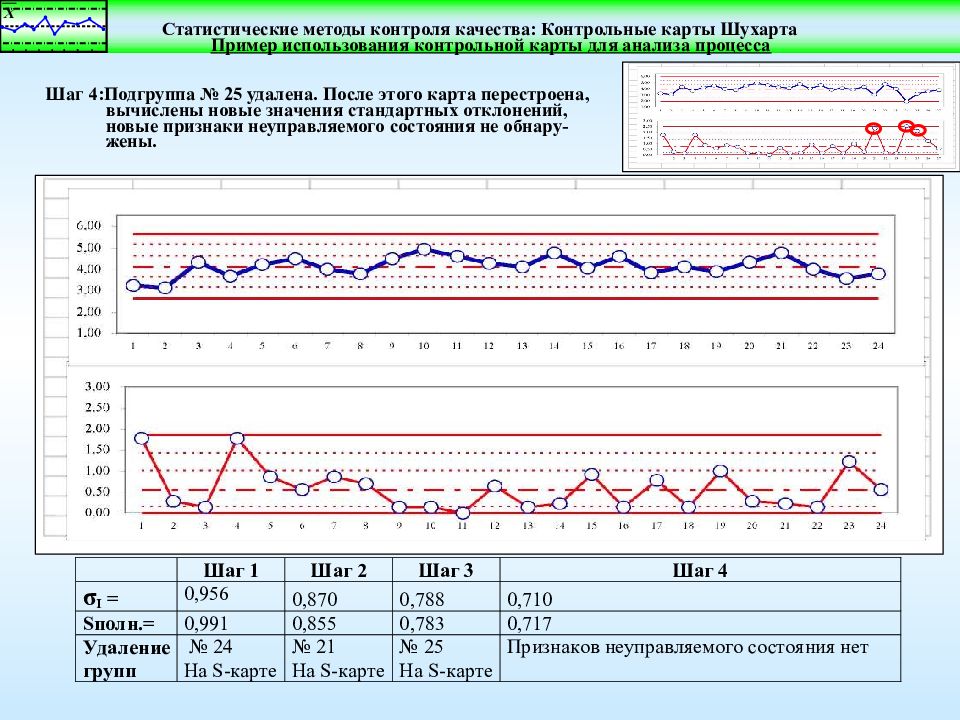
Пример использования контрольной карты для анализа процесса Шаг 4:Подгруппа № 25 удалена. После этого карта перестроена, вычислены новые значения стандартных отклонений, новые признаки неуправляемого состояния не обнару- жены.
Слайд 18
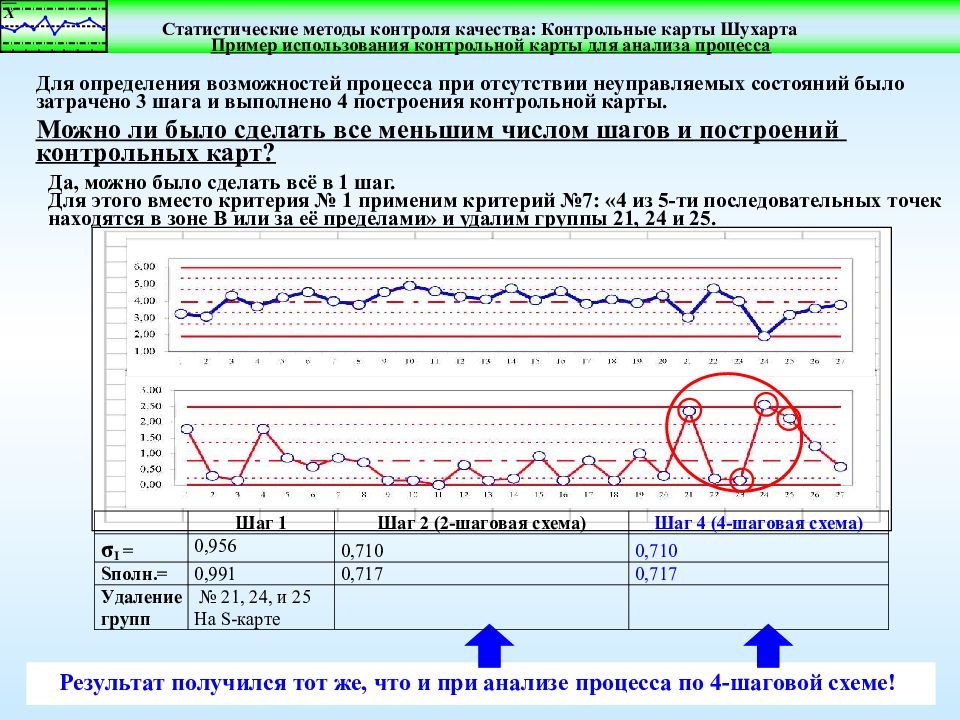
Пример использования контрольной карты для анализа процесса Для определения возможностей процесса при отсутствии неуправляемых состояний было затрачено 3 шага и выполнено 4 построения контрольной карты. Можно ли было сделать все меньшим числом шагов и построений контрольных карт? Да, можно было сделать всё в 1 шаг. Для этого вместо критерия № 1 применим критерий №7: «4 из 5-ти последовательных точек находятся в зоне В или за её пределами» и удалим группы 21, 24 и 25. Результат получился тот же, что и при анализе процесса по 4-шаговой схеме!