Первый слайд презентации: Лекция 4. Механика жидкостей и газов. Биомеханика. Акустика
Лектор. Войтик В. В.
Слайд 2: Механика жидкостей и газов
2 Механика жидкостей и газов +2 Понятие давления. Силы давления в жидкости. Линии и трубка тока. Линейная и объемная скорости стационарного движение идеальной несжимаемой жидкости. Закон Ньютона для внутреннего трения. Вязкость жидкости. Физический смысл динамического коэффициента вязкости. Ньютоновские и неньютоновские жидкости. Формулы Пуазейля для вязкой жидкости. Метод Стокса для определения вязкости (вывод). Ламинарный и турбулентный режимы течений жидкостей и газов. Число Рейнольдса.
Слайд 3: Понятие давления
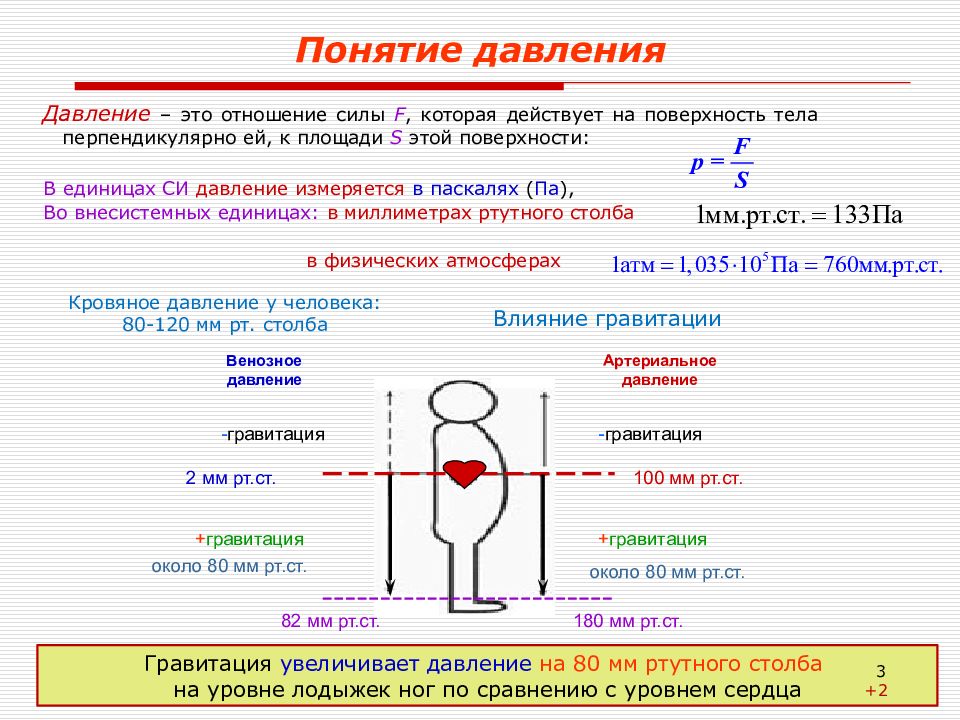
Лекция 8. Механика жидкости Давление – это отношение силы F, которая действует на поверхность тела перпендикулярно ей, к площади S этой поверхности: В единицах СИ давление измеряется в паскалях ( Па ), Во внесистемных единицах: в миллиметрах ртутного столба в физических атмосферах Венозное давление Артериальное давление + гравитация - гравитация + гравитация 100 мм рт.ст. 2 мм рт.ст. 82 мм рт.ст. 180 мм рт.ст. - гравитация около 80 мм рт.ст. около 80 мм рт.ст. Гравитация увеличивает давление на 80 мм ртутного столба на уровне лодыжек ног по сравнению с уровнем сердца Влияние гравитации Кровяное давление у человека: 80-120 мм рт. столба +2 3
Слайд 4: Основные понятия гидродинамики
4 Основные понятия гидродинамики Гидродинамика – наука о течении различных жидкостей. Основная задача гидродинамики – установить законы, которые определяют это течение. Для изучения законов течения используется слоистая модель жидкости: реальная текущая жидкость упрощённо представляется в виде набора слоёв, текущих друг над другом с разной скоростью v. Слои характеризуются линиями тока и трубками тока. +3
Слайд 5: Основные понятия гидродинамики (продолжение)
5 Основные понятия гидродинамики (продолжение) Линия тока – это линия, касательные к которой в каждой точке совпадают с направлением вектора скорости частиц жидкости в этой точке ( Рис.1а ). Трубка тока – это область жидкости, ограниченная по бокам линиями тока, а спереди и сзади секущими плоскостями, перпендикулярными направлению вектора скорости v ( Рис.1б ). Рис.1. Пояснение понятий « линия тока » (а) и « трубка тока » (б). 5
Слайд 6: Виды течения
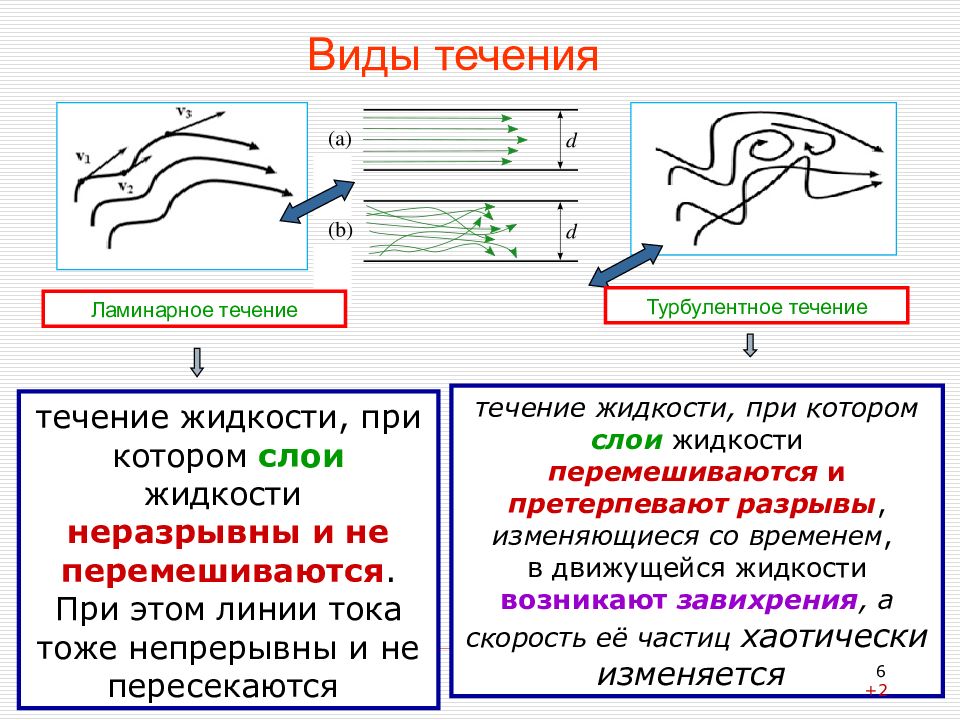
6 Виды течения течение жидкости, при котором слои жидкости неразрывны и не перемешиваются. При этом линии тока тоже непрерывны и не пересекаются течение жидкости, при котором слои жидкости перемешиваются и претерпевают разрывы, изменяющиеся со временем, в движущейся жидкости возникают завихрения, а скорость её частиц хаотически изменяется Ламинарное течение Турбулентное течение 6 +2
Слайд 7: Пример различия между ламинарным и турбулентным течением
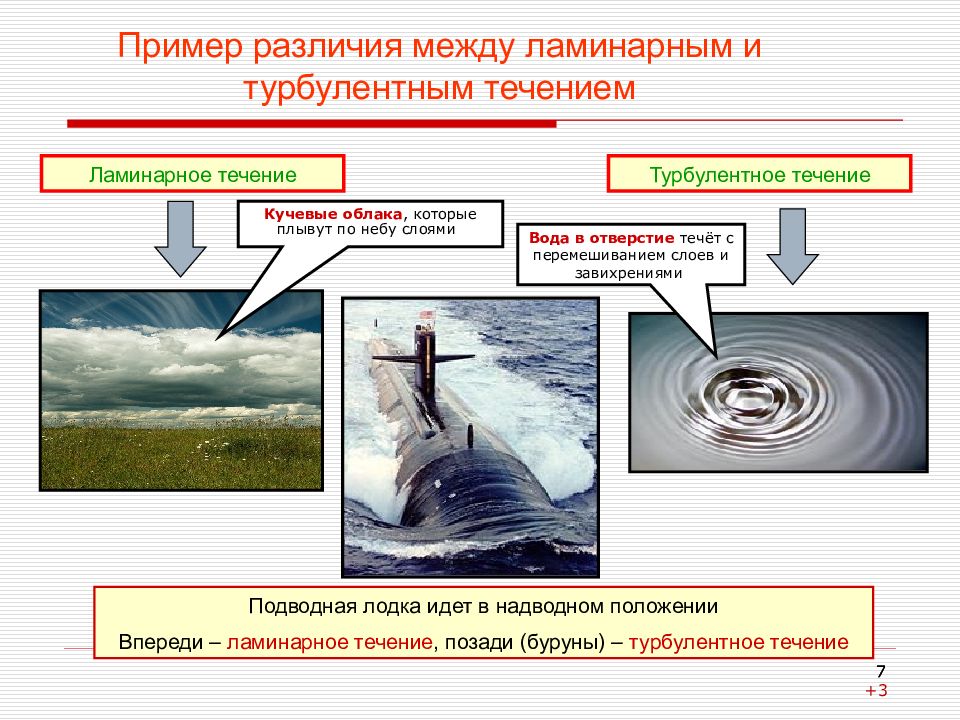
Подводная лодка идет в надводном положении Впереди – ламинарное течение, позади (буруны) – турбулентное течение 7 Кучевые облака, которые плывут по небу слоями Вода в отверстие течёт с перемешиванием слоев и завихрениями Ламинарное течение Турбулентное течение 7 +3
Слайд 8
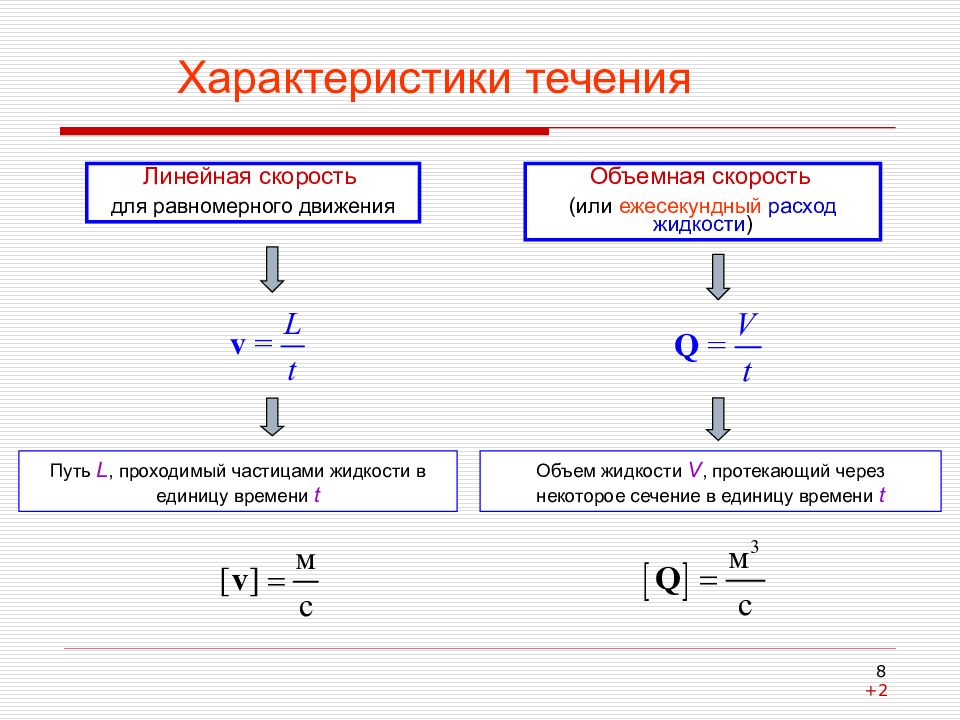
Характеристики течения Линейная скорость для равномерного движения Объемная скорость (или ежесекундный расход жидкости ) Путь L, проходимый частицами жидкости в единицу времени t Объем жидкости V, протекающий через некоторое сечение в единицу времени t 8 +2
Слайд 9: Вязкость жидкости
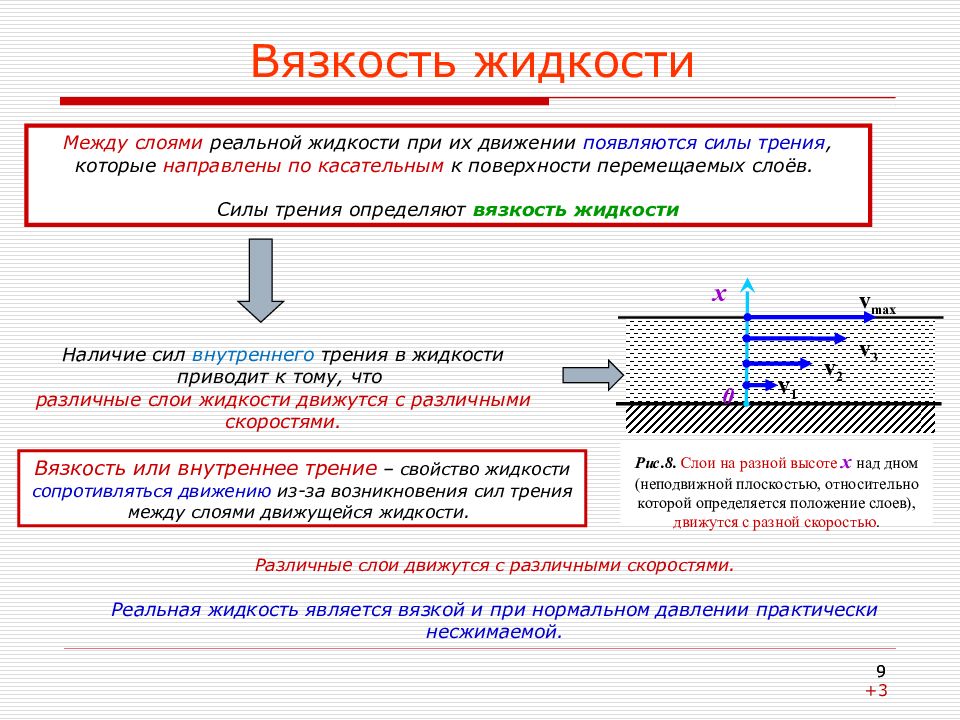
Различные слои движутся с различными скоростями. Реальная жидкость является вязкой и при нормальном давлении практически несжимаемой. Рис.8. Слои на разной высоте x над дном (неподвижной плоскостью, относительно которой определяется положение слоев), движутся с разной скоростью. x v max v 3 v 2 v 1 0 Вязкость или внутреннее трение – свойство жидкости сопротивляться движению из-за возникновения сил трения между слоями движущейся жидкости. 9 Вязкость жидкости Между слоями реальной жидкости при их движении появляются силы трения, которые направлены по касательным к поверхности перемещаемых слоёв. Силы трения определяют вязкость жидкости Наличие сил внутреннего трения в жидкости приводит к тому, что различные слои жидкости движутся с различными скоростями. 9 +3
Слайд 10: Градиент скорости
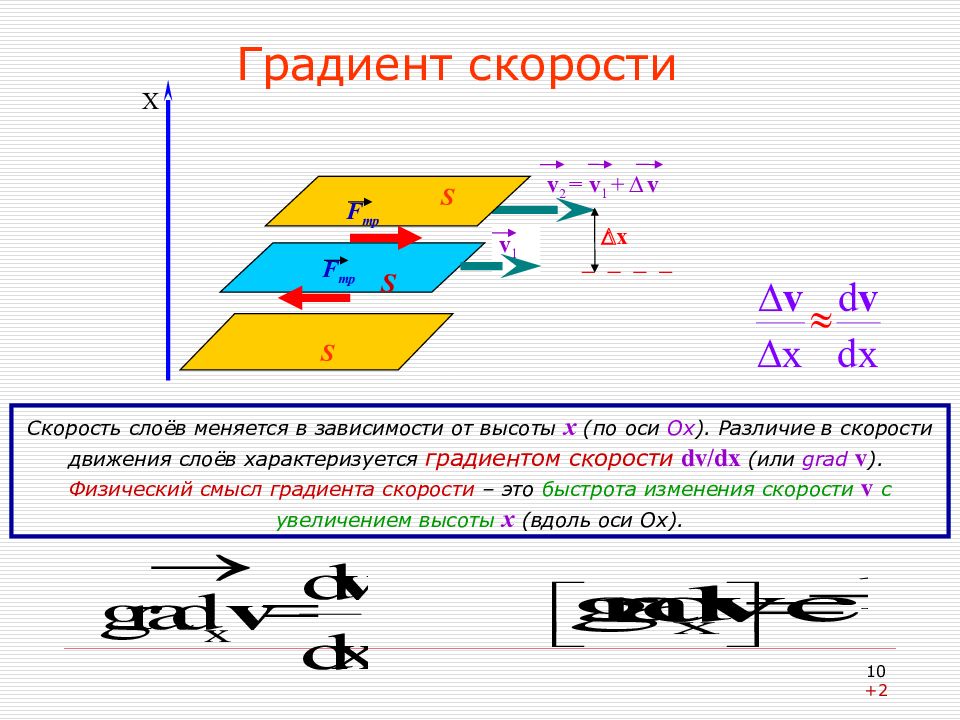
Скорость слоёв меняется в зависимости от высоты х (по оси Ох ). Различие в скорости движения слоёв характеризуется градиентом скорости dv / dx (или grad v ). Физический смысл градиента скорости – это быстрота изменения скорости v с увеличением высоты х (вдоль оси Ох). Градиент скорости v 1 v 2 = v 1 + v x S S S F тр F тр X 10 +2
Слайд 11: Закон Ньютона для вязкой жидкости
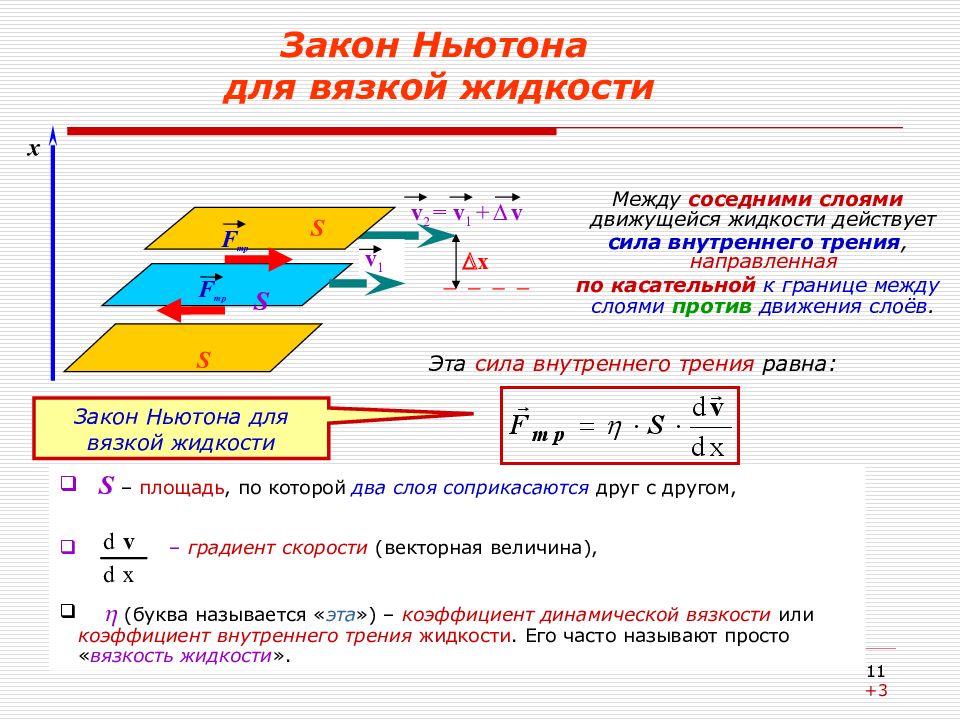
Между соседними слоями движущейся жидкости действует сила внутреннего трения, направленная по касательной к границе между слоями против движения слоёв. 11 Закон Ньютона для вязкой жидкости S – площадь, по которой два слоя соприкасаются друг с другом, – градиент скорости (векторная величина), (буква называется « эта ») – коэффициент динамической вязкости или коэффициент внутреннего трения жидкости. Его часто называют просто « вязкость жидкости ». v 1 v 2 = v 1 + v x S S S F тр F тр x Эта сила внутреннего трения равна: 11 +3
Слайд 12: Физический смысл коэффициента динамической вязкости
Выразим из закона Ньютона для вязкой жидкости коэффициент вязкости : Физический смысл коэффициента динамической вязкости : это сила внутреннего трения, возникающая между слоями площадью S =1 м 2 при градиенте скорости Жидкость с большой вязкостью Жидкость с малой вязкостью 12 Коэффициент вязкости зависит от : природы жидкости; температуры жидкости. Тело падает в жидкость. Разница в поведении жидкостей 12 +3
Слайд 13
Почему используют сантипуазы? Вязкость воды равна воды = 1 сП ( 1 мПа с ), а именно с водой удобно сравнивать вязкость других жидкостей в технике, медицине и биологии. Отношение называется относительной вязкостью жидкости (безразмерная величина). 13 Единицы измерения вязкости жидкости 13 +2
Слайд 14: Ньютоновские и неньютоновские жидкости
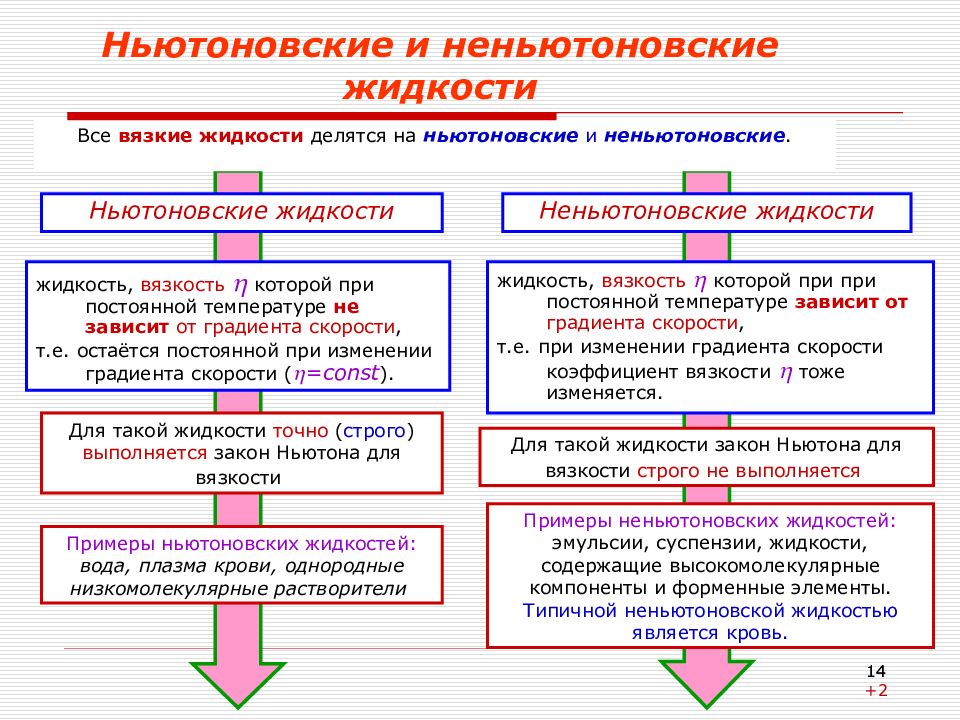
Ньютоновские жидкости Все вязкие жидкости делятся на ньютоновские и неньютоновские. Неньютоновские жидкости жидкость, вязкость которой при постоянной температуре не зависит от градиента скорости, т.е. остаётся постоянной при изменении градиента скорости ( = const ). жидкость, вязкость которой при при постоянной температуре зависит от градиента скорости, т.е. при изменении градиента скорости коэффициент вязкости тоже изменяется. Для такой жидкости точно ( строго ) выполняется закон Ньютона для вязкости Для такой жидкости закон Ньютона для вязкости строго не выполняется Примеры ньютоновских жидкостей: вода, плазма крови, однородные низкомолекулярные растворители Примеры неньютоновских жидкостей: эмульсии, суспензии, жидкости, содержащие высокомолекулярные компоненты и форменные элементы. Типичной неньютоновской жидкостью является кровь. 14 14 +2
Слайд 15: Формула Пуазейля для течения вязкой жидкости по цилиндрическим трубам
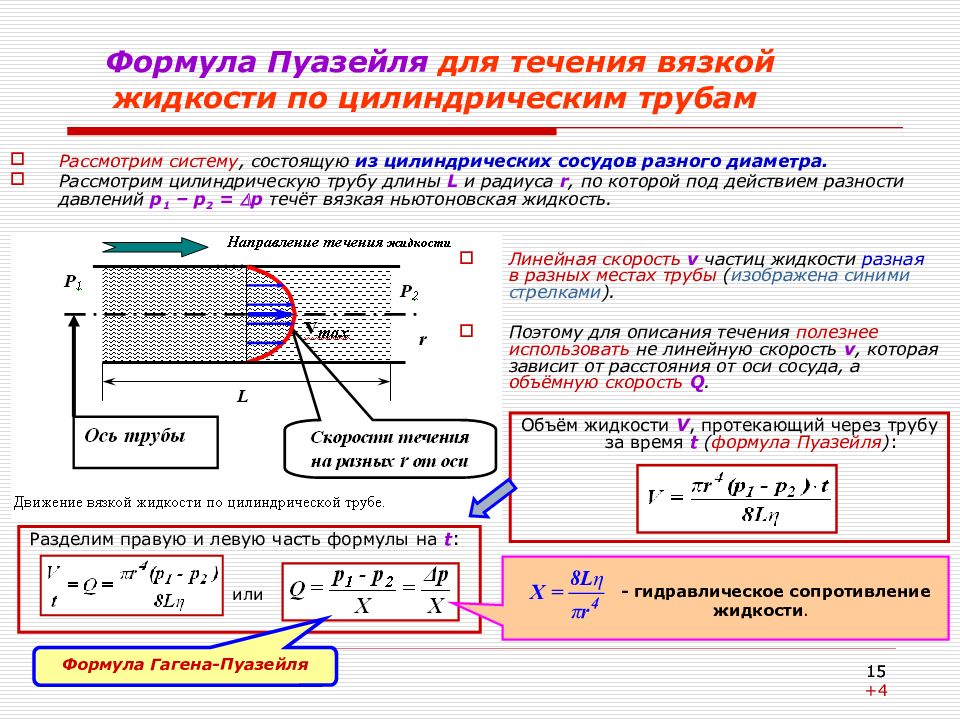
Рассмотрим систему, состоящую из цилиндрических сосудов разного диаметра. Рассмотрим цилиндрическую трубу длины L и радиуса r, по которой под действием разности давлений р 1 – р 2 = р течёт вязкая ньютоновская жидкость. 15 Формула Пуазейля для течения вязкой жидкости по цилиндрическим трубам Линейная скорость v частиц жидкости разная в разных местах трубы ( изображена синими стрелками ). Поэтому для описания течения полезнее использовать не линейную скорость v, которая зависит от расстояния от оси сосуда, а объёмную скорость Q. Объём жидкости V, протекающий через трубу за время t ( формула Пуазейля ) : Разделим правую и левую часть формулы на t : или - гидравлическое сопротивление жидкости. Формула Гагена-Пуазейля 15 +4
Слайд 16: Переход из ламинарного течения вязкой жидкости в турбулентное
Режим течения определяется значением числа Рейнольдса ( Re ). При течении вязкой жидкости по гладкой цилиндрической трубе число Рейнольдса равно: D – диаметр трубы, - плотность жидкости, v – средняя скорость её течения, - вязкость жидкости. Течение жидкости будет ламинарным, если число Рейнольдса Re будет не больше некоторого критического значения Re кр ( Re ≤ Re кр ) Течение жидкости становится турбулентным, если Re > Re кр Выше уже говорилось, что течение вязкой жидкости может быть ламинарным или турбулентным. 16 +2
Слайд 17: Методы определения вязкости
Приборы, которые применяются для определения вязкостей жидкости, - вискозиметры. 17 Методы определения вязкости 3. Ротационные Методы определения вязкости 2. Капиллярные 1. Метод Стокса (метод падающего шарика) 17
Слайд 18: БИОМЕХАНИКА – это раздел биофизики, изучающий механическое движение материи животных и человека под влиянием различных воздействий
Слайд 19: Деформация тела - изменение взаимного расположения материальных точек тела, которое приводит к изменению его формы и размеров
Слайд 20: В деформируемых биообъектах в результате противодействия приложенным внешним силам возникают внутренние силы, противоположные по направлению и отличающиеся по физической природе:
упругая сила сила внутреннего трения сила поверхностного натяжения
Слайд 21: Упругой называется сила, которая возникает в результате смещения частиц в новое положение равновесия. Частный случай упругости – эластичность
Слайд 23: Виды деформации
Продольная деформация – деформация, возникающая в стержне при действии силы, направленной вдоль его оси. Сдвиговая деформация –деформация, возникающая под действием силы, касательно приложенной к одной грани прямоугольного параллелепипеда, превращающая его в косоугольный параллелепипед.
Слайд 24
Упругие деформации подчиняются закону Гука Роберт Гук (1635 — 1703) — английский физик, член Лондонского королевского общества, его работы посвящены теплоте, упругости, оптике, небесной механике. Гук усовершенствовал микроскоп, что привело его к открытию клеточного строения организма.
Слайд 25
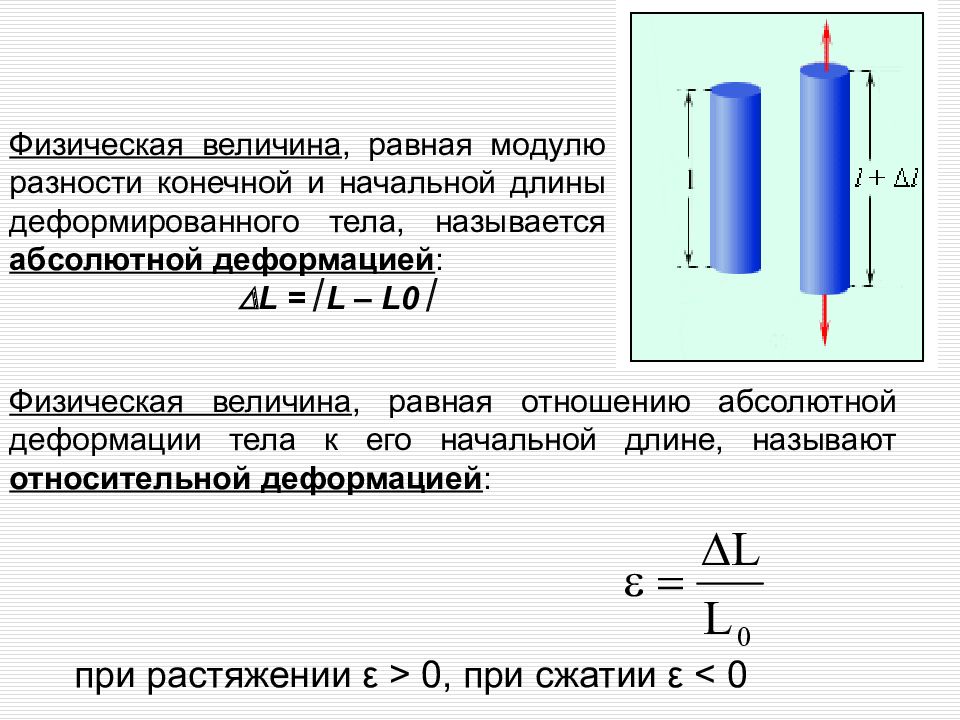
Физическая величина, равная модулю разности конечной и начальной длины деформированного тела, называется абсолютной деформацией : L = L – L0 Физическая величина, равная отношению абсолютной деформации тела к его начальной длине, называют относительной деформацией : при растяжении ε > 0, при сжатии ε < 0
Слайд 26
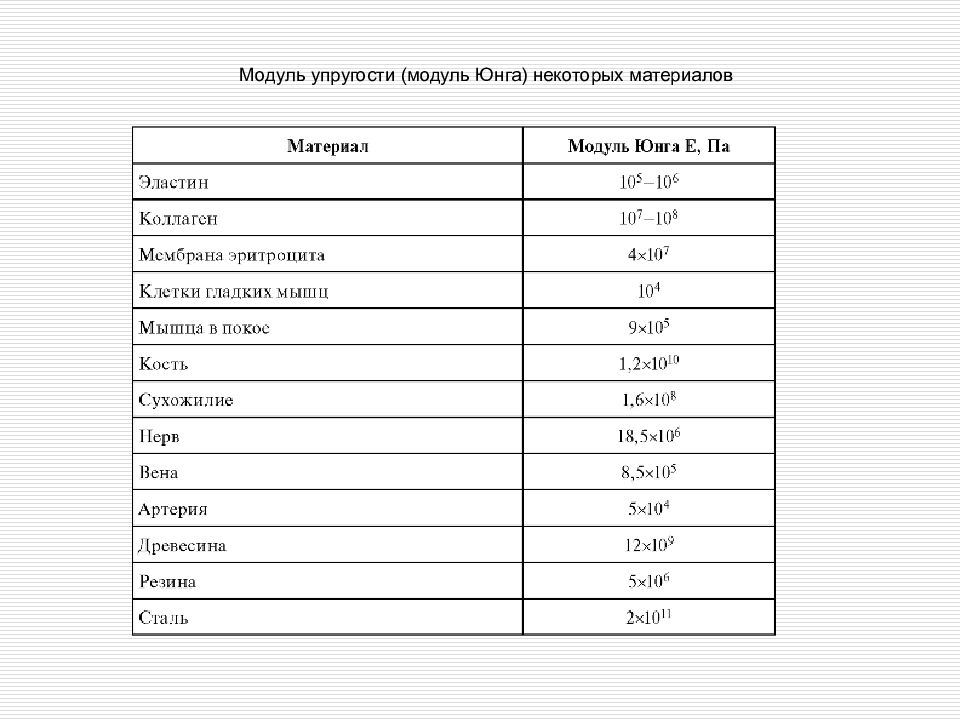
Закон Гука для деформации растяжение - сжатие коэффициент пропорциональности Е, входящем в закон Гука, называется модулем упругости или модулем Юнга. Е=1 [ Па ] механическое напряжение
Слайд 27: Модуль Юнга представляет собой упругую характеристику материала, из которого сделано деформируемое тело
E= / е, [ E ] = 1 Н/м 2
Слайд 28: Модуль упругости, представленный коэффициентом Пуассона
Δ l /l = - Δ h/ Δ h, где Δ l/l – относительная деформация растяжения - Δ h/ Δ h – относительная деформация поперечного укорочения -коэффициент Пуассона Связывает относительную деформацию рас-тяжения с относительной деформацией поперечного укорочения =0,25-0,5
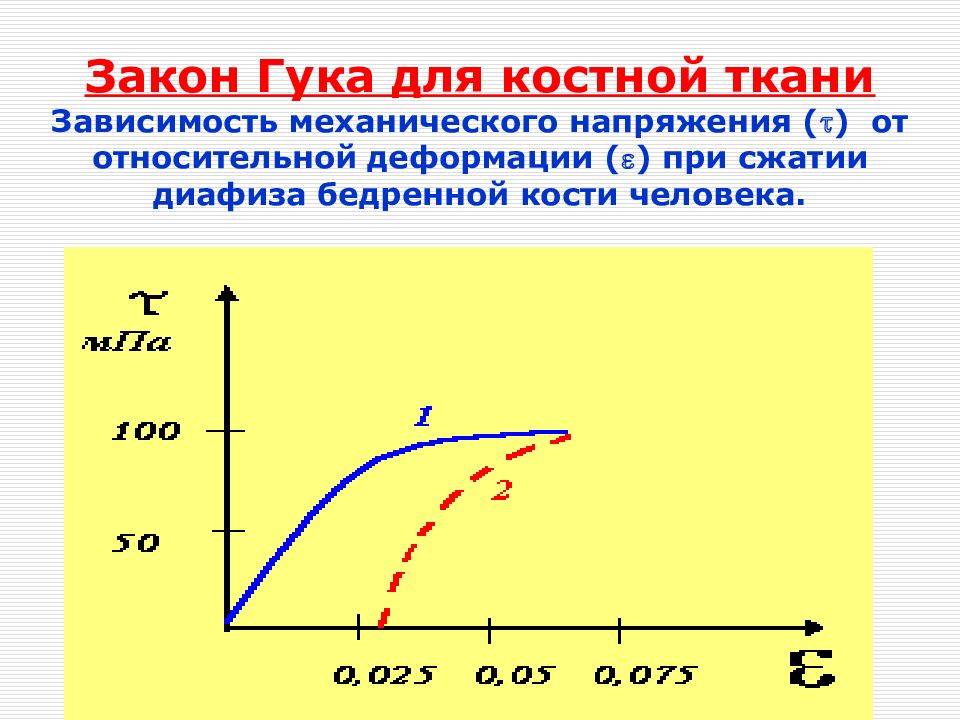
Слайд 29: Закон Гука для костной ткани Зависимость механического напряжения ( ) от относительной деформации ( ) при сжатии диафиза бедренной кости человека
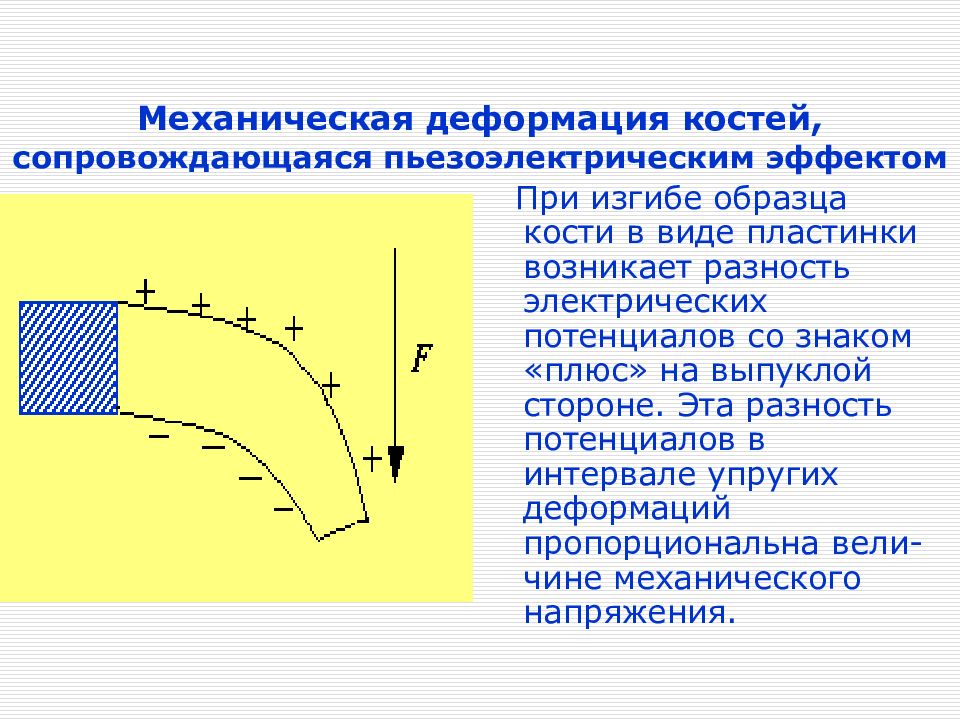
Слайд 30: Механическая деформация костей, сопровождающаяся пьезоэлектрическим эффектом
При изгибе образца кости в виде пластинки возникает разность электрических потенциалов со знаком «плюс» на выпуклой стороне. Эта разность потенциалов в интервале упругих деформаций пропорциональна вели-чине механического напряжения.
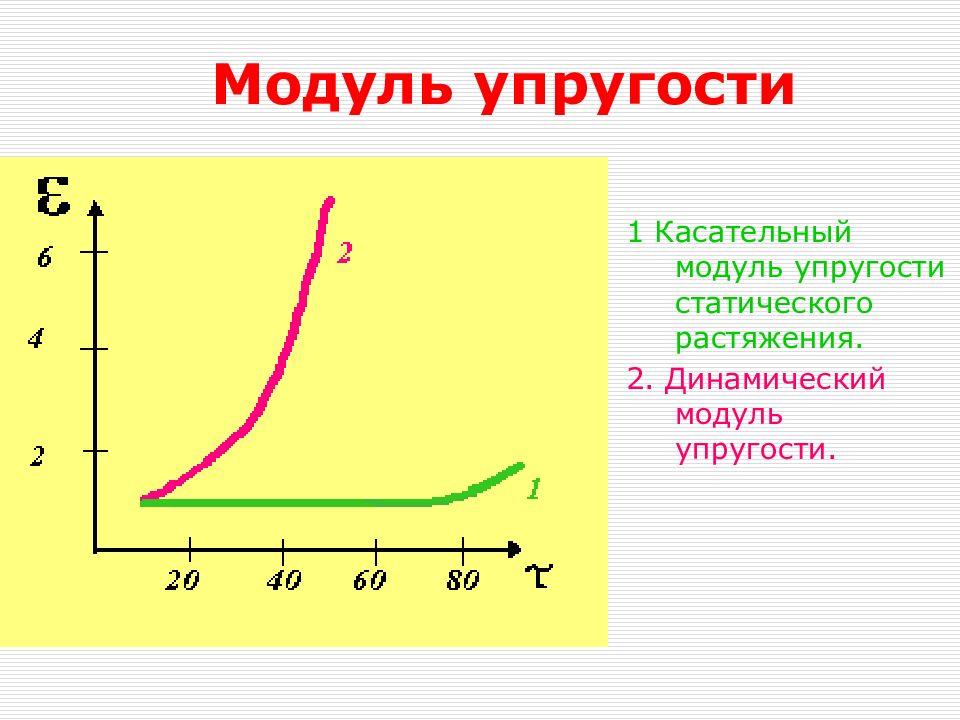
Слайд 31: Модуль упругости
1 Касательный модуль упругости статического растяжения. 2. Динамический модуль упругости.
Слайд 32: Виды мышечного сокращения
Изометрическое – происходит при неизменной длине мышц. Изотоническое -происходит при неизменном напряжении.
Слайд 33
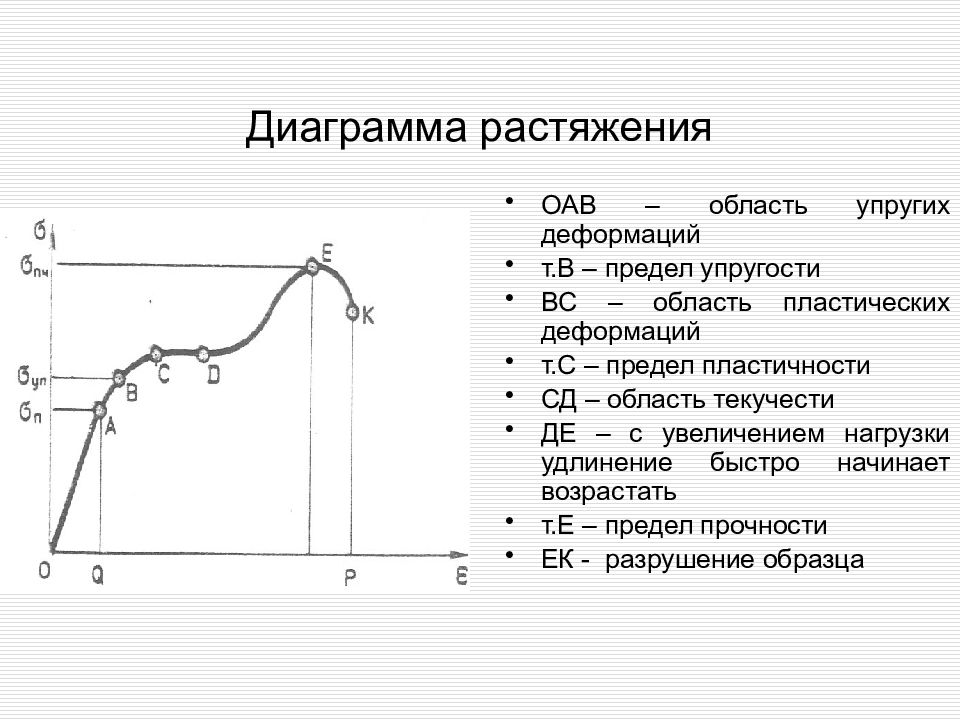
Диаграмма растяжения ОАВ – область упругих деформаций т.В – предел упругости ВС – область пластических деформаций т.С – предел пластичности СД – область текучести ДЕ – с увеличением нагрузки удлинение быстро начинает возрастать т.Е – предел прочности ЕК - разрушение образца
Слайд 34: Механические свойства биологических тканей
процессы биологической подвижности: сокращение мышц животных, рост клеток, движение хромосом в клетках при их делении и др., называют активными механическими свойствами биологических систем рассматриваются в курсе биохимии пассивные механические свойства биологических тел рассматриваются в курсе биофизики
Слайд 35
ткани человека подразделяют по плотности и типу пространственной структуры на твердые (кость, эмаль и дентин зубов); мягкие (мышцы, эпителий, эндотелий, соединительная ткань, паренхима); жидкие (кровь, лимфа, ликвор, слюна, сперма).
Слайд 37: АКУСТИКА. ЗВУК
Звук в широком смысле - упругие колебания и волны, распространяющиеся в газообразных, жидких и твердых веществах; в узком смысле - явление, субъективно воспринимаемое органами слуха человека и животных.
Слайд 38
Звук с частотой ниже 16-20 Гц называется инфразвуком, выше 20 кГц -ультразвуком, а самые высокочастотные упругие волны в диапазоне от 109 до 1012 Гц - гиперзвуком. Звуки, встречающиеся в природе, разделяют на несколько видов. Тон - это звук, представляющий собой периодический процесс. Основной характеристикой тона является частота. Простой тон создается телом, колеблющимся по гармоническому закону (например, камертоном). Сложный тон создается периодическими колебаниями, которые не являются гармоническими (например, звук музыкального инструмента, звук, создаваемый речевым аппаратом человека). Шум - это звук, имеющий сложную неповторяющуюся временную зависимость и представляющий собой сочетание беспорядочно изменяющихся сложных тонов (шелест листьев).
Слайд 39
Звуковой удар - это кратковременное звуковое воздействие (хлопок, взрыв, удар, гром). Сложный тон, как периодический процесс, можно представить в виде суммы простых тонов (разложить на составляющие тоны). Такое разложение называется спектром. Акустический спектр тона - это совокупность всех его частот с указанием их относительных интенсивностей или амплитуд. Наименьшая частота в спектре (ν) соответствует основному тону, а остальные частоты называют обертонами или гармониками. Обертоны имеют частоты, кратные основной частоте: 2ν, 3ν, 4ν,...
Слайд 40
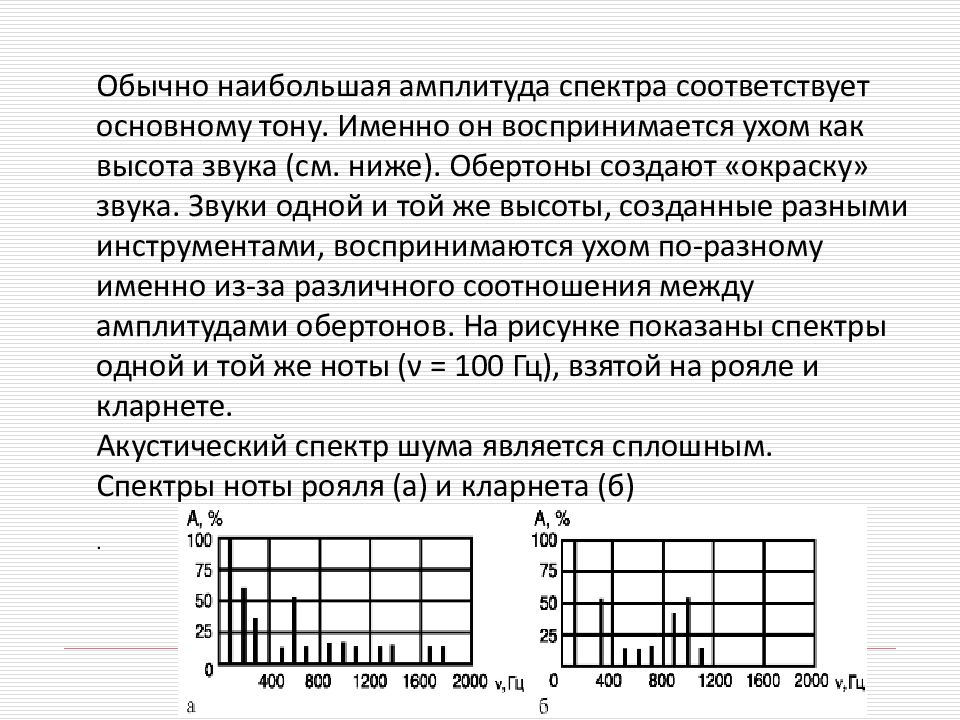
Обычно наибольшая амплитуда спектра соответствует основному тону. Именно он воспринимается ухом как высота звука (см. ниже). Обертоны создают «окраску» звука. Звуки одной и той же высоты, созданные разными инструментами, воспринимаются ухом по-разному именно из-за различного соотношения между амплитудами обертонов. На рисунке показаны спектры одной и той же ноты (ν = 100 Гц), взятой на рояле и кларнете. Акустический спектр шума является сплошным. Спектры ноты рояля (а) и кларнета (б) .
Слайд 41
Физические характеристики звука 1. Скорость (v). Звук распространяется в любой среде, кроме вакуума. Скорость его распространения зависит от упругости, плотности и температуры среды, но не зависит от частоты колебаний. Скорость звука в газе зависит от его молярной массы (М) и абсолютной температуры (Т):
Слайд 42
Скорость звука в воде равна 1500 м/с; близкое значение имеет скорость звука и в мягких тканях организма. 2. Звуковое давление. Распространение звука сопровождается изменением давления в среде. Именно изменения давления вызывают колебания барабанной перепонки, которые и определяют начало такого сложного процесса, как возникновение слуховых ощущений. Звуковое давление (ΔΡ) - это амплитуда тех изменений давления в среде, которые возникают при прохождении звуковой волны. 3. Интенсивность звука (I). Распространение звуковой волны сопровождается переносом энергии.
Слайд 43
Интенсивность звука - это плотность потока энергии, переносимой звуковой волной. В однородной среде интенсивность звука, испущенного в данном направлении, убывает по мере удаления от источника звука. При использовании волноводов можно добиться и увеличения интенсивности. Типичным примером такого волновода в живой природе является ушная раковина. Связь между интенсивностью (I) и звуковым давлением (ΔΡ) выражается следующей формулой: где ρ - плотность среды; v - скорость звука в ней.
Слайд 44
Минимальные значения звукового давления и интенсивности звука, при которых у человека возникают слуховые ощущения, называются порогом слышимости. Для уха среднего человека на частоте 1 кГц порогу слышимости соответствуют следующие значения звукового давления (ΔΡ o ) и интенсивности звука (I o ): ΔΡ o = 3х10-5 Па (≈ 2х10-7 мм рт.ст.); I o = 10-12 Вт/м2. Значения звукового давления и интенсивности звука, при которых у человека возникают выраженные болевые ощущения, называются порогом болевого ощущения. Для уха среднего человека на частоте 1 кГц порогу болевого ощущения соответствуют следующие значения звукового давления (ΔΡm) и интенсивности звука (Im):
Слайд 45
4. Уровень интенсивности (L). Отношение интенсивностей, соответствующих порогам слышимости и болевого ощущения, столь велико (Im /I0 = 1013), что на практике используют логарифмическую шкалу, вводя специальную безразмерную характеристику - уровень интенсивности. Уровнем интенсивности называют десятичный логарифм отношения интенсивности звука к порогу слышимости: Единицей измерения уровня интенсивности является бел (Б). Обычно используют более мелкую единицу уровня интенсивности - децибел (дБ): 1 дБ = 0,1 Б. Уровень интенсивности в децибелах вычисляется :
Слайд 46
Логарифмический характер зависимости уровня интенсивности от самой интенсивности означает, что при увеличении интенсивности в 10 раз уровень интенсивности возрастает на 10 дБ. Если человек слышит звуки, приходящие с одного направления от нескольких некогерентных источников, то их интенсивности складываются :
Слайд 47
Высокий уровень интенсивности звука приводит к необратимым изменениям в слуховом аппарате. Так, звук в 160 дБ может вызвать разрыв барабанной перепонки и смещение слуховых косточек в среднем ухе, что приводит к необратимой глухоте. При 140 дБ человек ощущает сильную боль, а продолжительное действие шума в 90-120 дБ приводит к поражению слухового нерва.
Слайд 48: Характеристики слухового ощущения. Звуковые измерения
Звук является объектом слухового ощущения. Он оценивается человеком субъективно. Все субъективные характеристики слухового ощущения связаны с объективными характеристиками звуковой волны. Высота, тембр. Воспринимая звуки, человек различает их по высоте и тембру. Высота тона обусловлена прежде всего частотой основного тона (чем больше частота, тем более высоким воспринимается звук). В меньшей степени высота зависит от интенсивности звука (звук большей интенсивности воспринимается более низким).
Слайд 49
Тембр - это характеристика звукового ощущения, которая определяется его гармоническим спектром. Тембр звука зависит от числа обертонов и от их относительных интенсивностей. Закон Вебера-Фехнера. Громкость звука Использование логарифмической шкалы для оценки уровня интенсивности звука хорошо согласуется с психофизическим законом Вебера-Фехнера: Если увеличивать раздражение в геометрической прогрессии (т.е. в одинаковое число раз), то ощущение этого раздражения возрастает в арифметической прогрессии (т.е. на одинаковую величину).
Слайд 50
Громкостью звука называют интенсивность (силу) слуховых ощущений. Ухо человека имеет различную чувствительность к звукам различных частот. Для учета этого обстоятельства можно выбрать некоторую опорную частоту, а восприятие остальных частот сравнивать с нею. По договоренности опорную частоту приняли равной 1 кГц (по этой причине и порог слышимости I0 установлен для этой частоты). Для чистого тона с частотой 1 кГц громкость (Е) принимают равной уровню интенсивности в децибелах:
Слайд 51
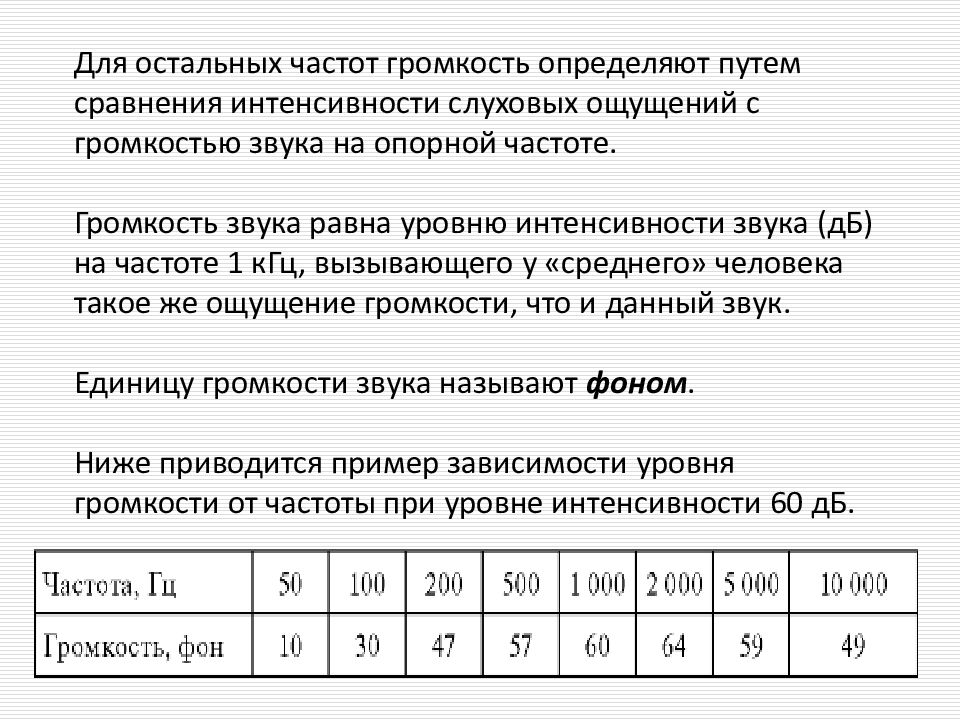
Для остальных частот громкость определяют путем сравнения интенсивности слуховых ощущений с громкостью звука на опорной частоте. Громкость звука равна уровню интенсивности звука (дБ) на частоте 1 кГц, вызывающего у «среднего» человека такое же ощущение громкости, что и данный звук. Единицу громкости звука называют фоном. Ниже приводится пример зависимости уровня громкости от частоты при уровне интенсивности 60 дБ.
Слайд 52
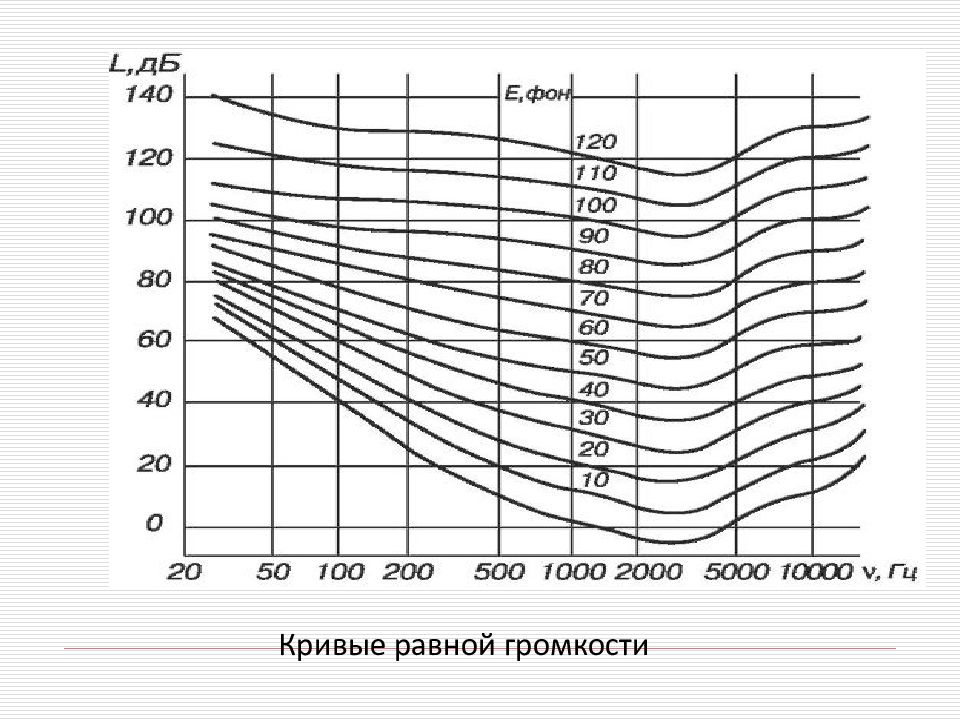
Кривые равной громкости Детальную связь между частотой, громкостью и уровнем интенсивности изображают графически с помощью кривых равной громкости. Эти кривые демонстрируют зависимость уровня интенсивности LдБ от частоты ν звука при заданной громкости звука. Нижняя кривая соответствует порогу слышимости. Она позволяет найти пороговое значение уровня интенсивности (Е = 0) при заданной частоте тона. С помощью кривых равной громкости можно найти громкость звука, если известны его частота и уровень интенсивности.
Слайд 54
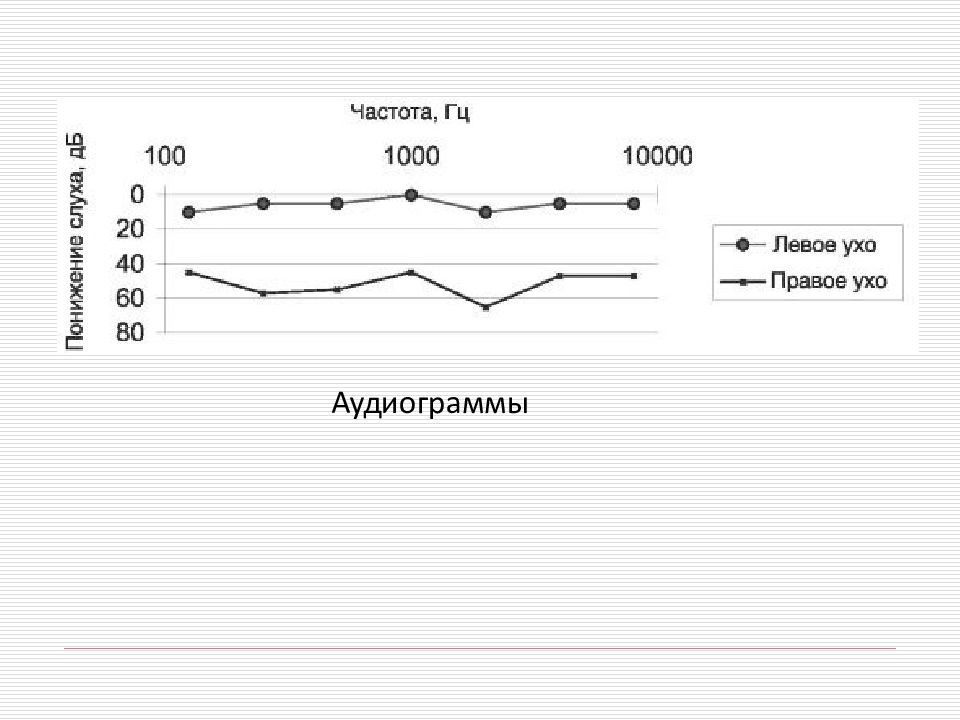
Звуковые измерения Кривые равной громкости отражают восприятие звука средним человеком. Для оценки слуха конкретного человека применяется метод тональной пороговой аудиометрии.Аудиометрия - метод измерения остроты слуха. На специальном приборе (аудиометре) определяется порог слухового ощущения, или порог восприятия, LП на разных частотах. Для этого с помощью звукового генератора создают звук заданной частоты и, увеличивая уровень интенсивности L, фиксируют пороговый уровень интенсивность Lп, при котором у испытуемого появляются слуховые ощущения. Меняя частоту звука, получают экспериментальную зависимость Lп(v), которую называют аудиограммой.
Слайд 56: Задачи
1. Звук, которому на улице соответствует уровень интенсивности L1 = 50 дБ, слышен в комнате так, как звук с уровнем интенсивности L2 = 30 дБ. Найти отношение интенсивностей звука на улице и в комнате. 2. Уровень громкости звука частотой 5000 Гц равен Е = 50 фон. Найти интенсивность этого звука, воспользовавшись кривыми равной громкости.
Слайд 57
Решение Из рисунка 3.2 находим, что на частоте 5000 Гц громкости Е =50 фон соответствует уровень интенсивности L = 47 дБ = 4,7 Б. Из формулы 3.4 находим: I = 104,7 I0 = 510-8 Вт/м2. 3. Вентилятор создает звук, уровень интенсивности которого L = 60 дБ. Найти уровень интенсивности звука при работе двух рядом стоящих вентиляторов. Решение L2 = lg(2x10L) = lg2 + L = 0,3 + 6Б = 63 дБ (см. 3.6). Ответ: L2 = 63 дБ.
Слайд 58
4. Уровень громкости звука реактивного самолета на расстоянии 30 м от него равен 140 дБ. Каков уровень громкости на расстоянии 300 м? Отражением от земли пренебречь. Решение Интенсивность убывает пропорционально квадрату расстояния - уменьшается в 102 раз. L1 - L2 = 10xlg(I1/I2) = 10x2 = 20 дБ. Ответ: L2 = 120 дБ. 5. Отношение интенсивностей двух источников звука равно: I2/I1 = 2. Чему равна разность уровней интенсивностей этих звуков? Решение ΔL = 10xlg(I2/I0) - 10xlg(I1/I0) = 10xlg(I2/I1) = 10xlg2 = 3 дБ. Ответ: 3 дБ.
Слайд 59
7. Амплитуда звуковой волны увеличилась в три раза. а) во сколько раз возросла ее интенсивность? б) на сколько децибел увеличился уровень громкости? Решение Интенсивность пропорциональна квадрату амплитуды 8. В лабораторном помещении, находящемся в цехе, уровень интенсивности шума достигал 80 дБ. С целью уменьшения шума было решено обить стены лаборатории звукопоглощающим материалом, уменьшающим интенсивность звука в 1500 раз. Какой уровень интенсивности шума станет после этого в лаборатории? Решение