Первый слайд презентации: Семинар 1 Элементы теории верятностей
Слайд 2: Случайное событие
Событие называется случайным, если оно при данных условиях может либо произойти, либо не произойти Каждое явление, в котором может осуществиться или не осуществиться случайное событие, называется испытанием
Слайд 3: Случайное событие
Относительная частота события h = m/n n – число испытаний m – число успехов Вероятность события p = h при n →∞ 0 ≤ p ≤ 1 p = 0 – невозможное событие p = 1 – достоверное событие Вероятность ненаступления события q =1- p
Слайд 4: Случайная величина
Закон (функция) вероятностей для дискретной случайной величины Значения случайной величины x : x 1, x 2, …, x k, … Вероятности значений p : p 1, p 2, …, p k, … Плотность (функция) вероятностей для непрерывной случайной величины p = p(x)
Дискретная случайная величина Непрерывная случайная величина F ( x )= P ( x ≤ X )
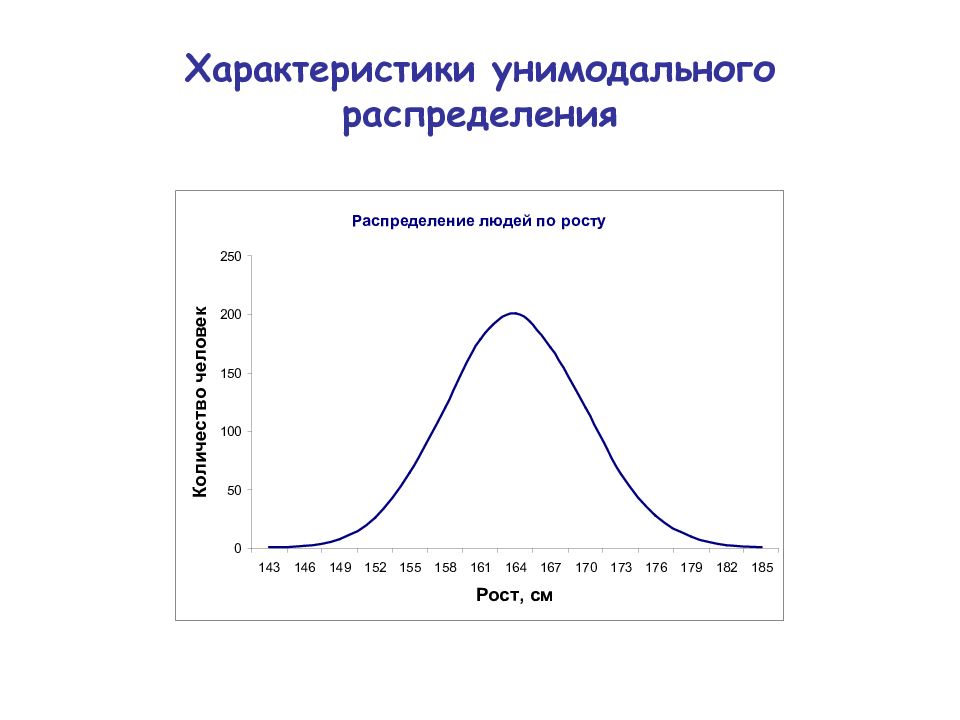
Слайд 7: Характеристики унимодального распределения
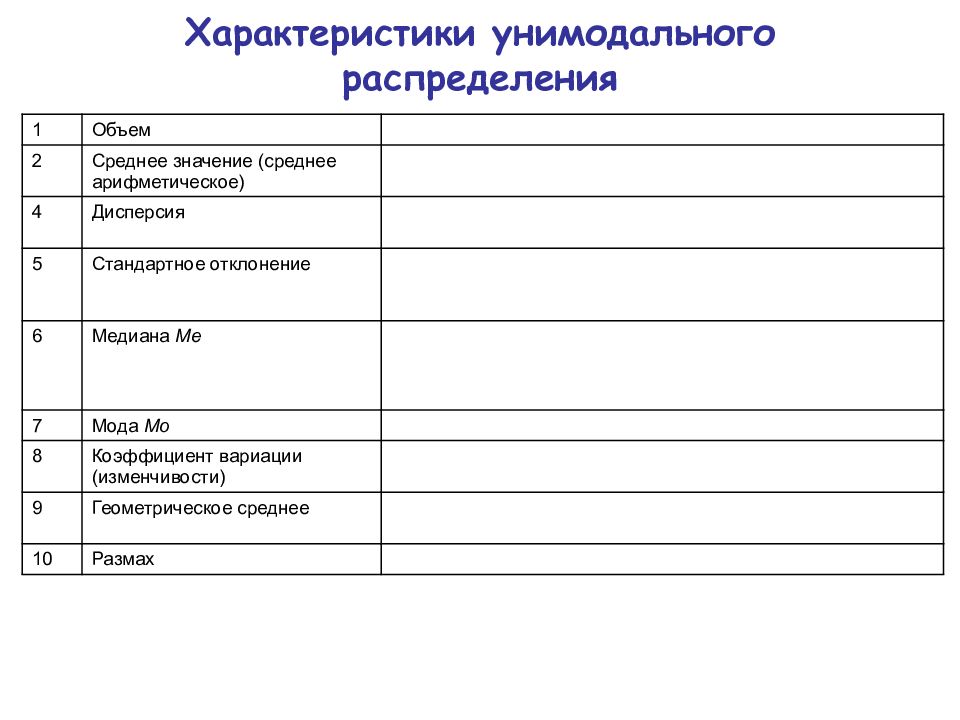
1 Объем 2 Среднее значение (среднее арифметическое) 4 Дисперсия 5 Стандартное отклонение 6 Медиана Me 7 Мода Mo 8 Коэффициент вариации (изменчивости) 9 Геометрическое среднее 10 Размах Характеристики унимодального распределения
Слайд 8: Характеристики унимодального распределения
1 Объем N 2 Среднее значение (среднее арифметическое) 3 Отклонение от среднего 4 Стандартное отклонение 5 Дисперсия 6 Медиана Me величина, которая делит распределение на две равные части таким образом, что каждая часть содержит 50% всего распределения 7 Мода Mo равна тому значению, частота которого максимальна Характеристики унимодального распределения Пример: 4 6 2 5 3 8 2 1 4 5
Слайд 9: Характеристики унимодального распределения
8 Коэффициент вариации (изменчивости) 9 Геометрическое среднее 10 Размах R = x max - x min 11 Взвешенное среднее 12 Взвешенное стандартное отклонение Характеристики унимодального распределения Пример: n1=8 x1=9 s1 2 =4 n2=10 x2=7 s2 2 =1 n3=6 x3=8 s3 2 =4
Слайд 10: Характеристики унимодального распределения
13. Арифметическое среднее с весами Измерения неравной точности
Слайд 12
Дискретные распределения 1. Биномиальное распределение (распределение Бернулли) для каждого испытания существует только два возможных исхода: Успех – вероятность p Неудача – вероятность q=1-p вероятность того, что в n опытах успех наступит x раз (а неудача – n - x раз) Параметры распределения – p, n С реднее значение μ= np Дисперсия σ 2 = np (1- p ) = npq P n, p ( x )= C x n p x q n - x
Слайд 13
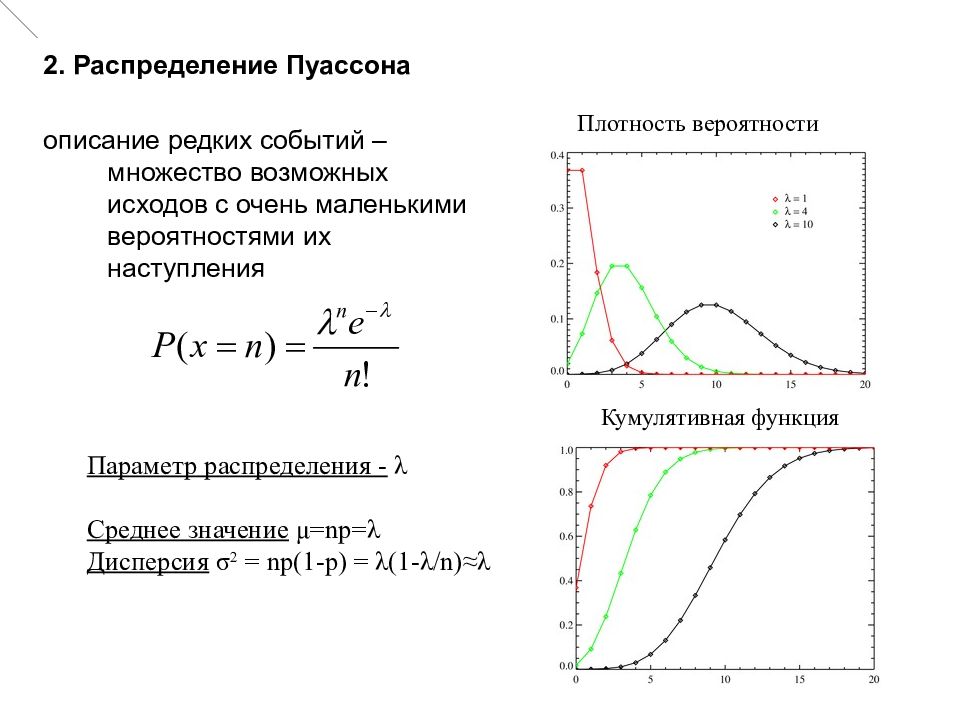
2. Распределение Пуассона описание редких событий – множество возможных исходов с очень маленькими вероятностями их наступления Параметр распределения - λ Среднее значение μ= np = λ Дисперсия σ 2 = np (1- p ) = λ(1-λ/n) ≈ λ Функция вероятности Функция распределения Плотность вероятности Кумулятивная функция
Слайд 14
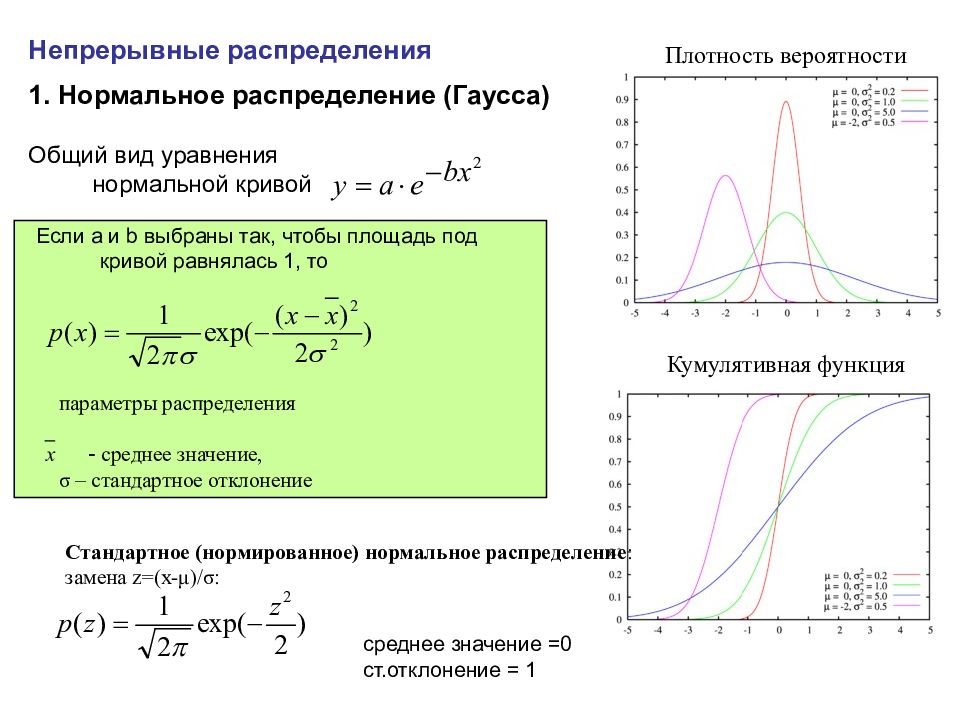
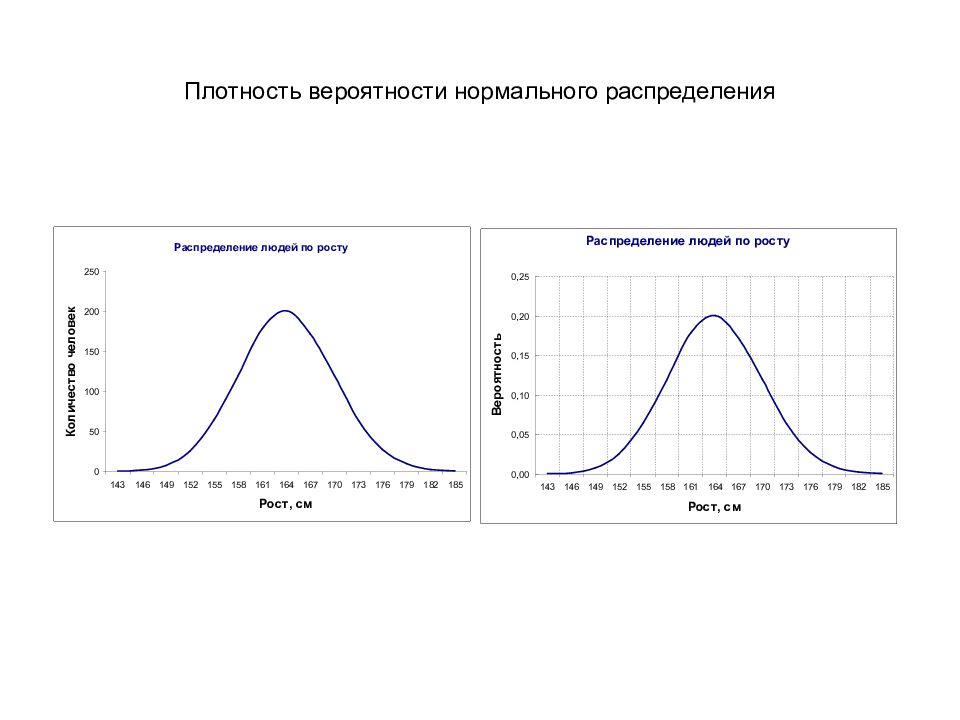
Непрерывные распределения 1. Нормальное распределение (Гаусса) Общий вид уравнения нормальной кривой параметры распределения - среднее значение, σ – стандартное отклонение среднее значение =0 ст.отклонение = 1 Если a и b выбраны так, чтобы площадь под кривой равнялась 1, то Плотность вероятности Кумулятивная функция Стандартное (нормированное) нормальное распределение : замена z =( x - μ )/ σ :
Слайд 16
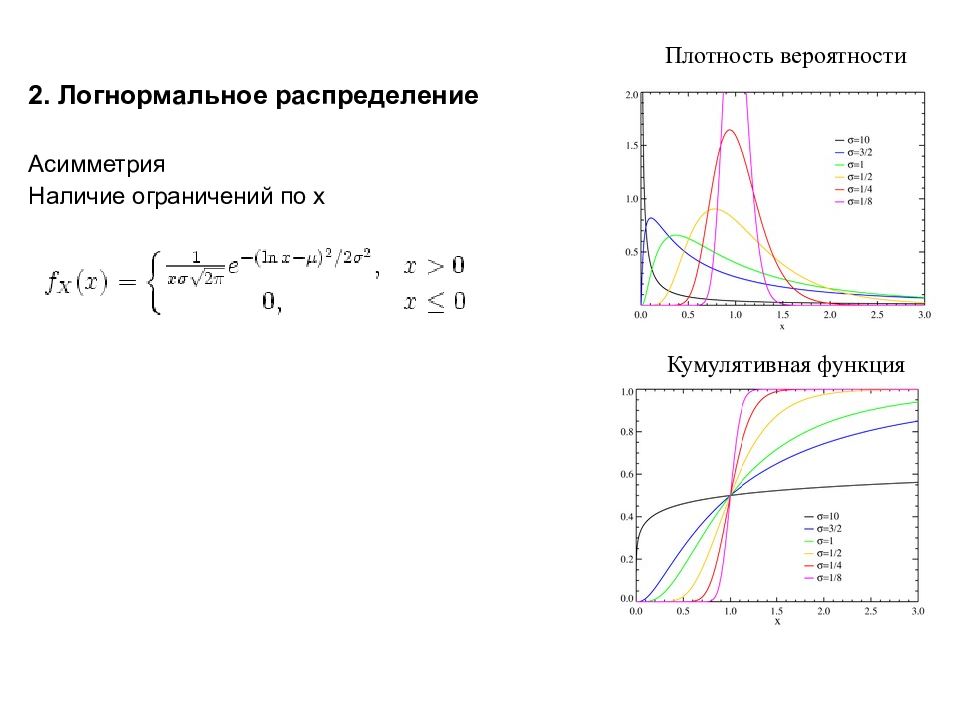
2. Логнормальное распределение Асимметрия Наличие ограничений по x Плотность вероятности Кумулятивная функция
Слайд 18: СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ
1. Оценка параметров по выборочным данным Выборка и генеральная совокупность. основные характеристики ВЫБОРОЧНОЙ совокупности: Среднее значение (среднее арифметическое) Стандартное отклонение Дисперсия : . основные характеристики ГЕНЕРАЛЬНОЙ совокупности: Генеральное среднее μ Стандартное отклонение генерального среднего σ выборочные параметры являются статистическими оценками генеральных параметров
Слайд 19
Чем больше объем выборки, тем меньше вероятность того, что выборочное среднее будет значительно отличаться от генерального среднего с ростом объема выборки оценки параметров стремятся к параметрам генеральной совокупности стандартная ошибка среднего показывает, насколько выборочное значение может отклоняться от генерального 2. Стандартная ошибка среднего Результаты записывают в виде
Слайд 20
Стандартные ошибки сложных средних Если z = a + x, где a – константа, x – переменная, то Если z = ax z = a e bx z = a lg ( bx ), z = x m z = x ± y
Слайд 21
Стандартные ошибки сложных средних z = xy или z = x / y Закон преобразования ошибок степенных произведений. Пусть h = kx a y b z c … где x, y, z – переменные, k, a, b, c – константы средняя относительная ошибка
Слайд 22
3. Доверительный интервал Интервал, в котором с заданной вероятностью заключен параметр генеральной совокупности (например, генеральное среднее), называется доверительным выборочные параметры являются статистическими оценками генеральных параметров Для случайной величины, подчиняющейся нормальному распределению: Вероятность того, что интервал содержит генеральное среднее равна площади под кривой плотности распределения от до
Слайд 23
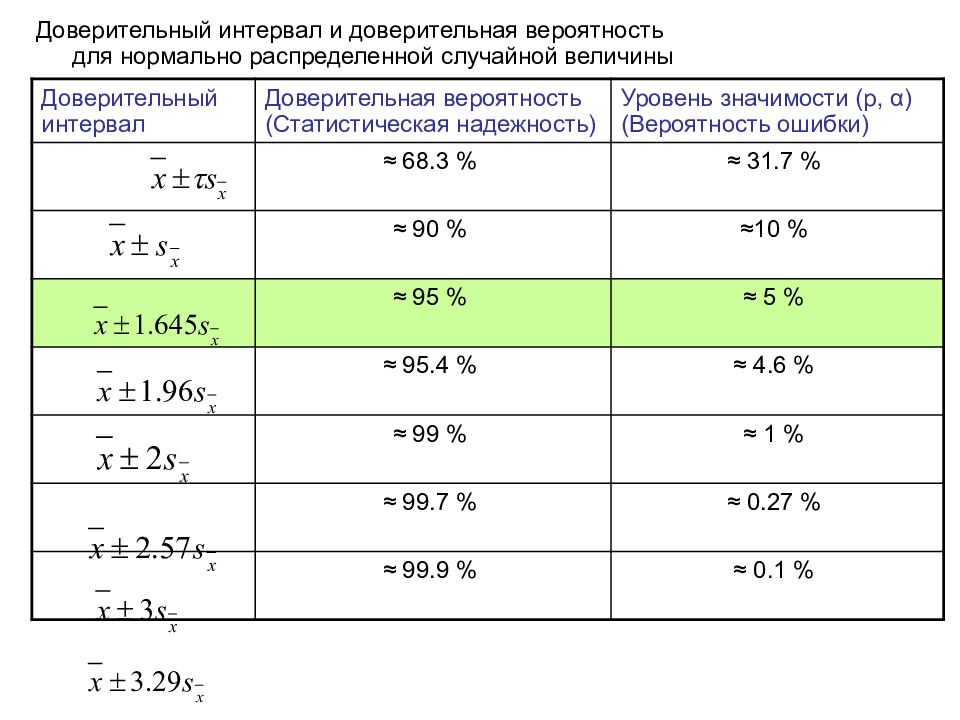
Доверительный интервал и доверительная вероятность для нормально распределенной случайной величины Доверительный интервал Доверительная вероятность (Статистическая надежность) Уровень значимости ( p, α ) (Вероятность ошибки) ≈ 68.3 % ≈ 31.7 % ≈ 90 % ≈ 10 % ≈ 95 % ≈ 5 % ≈ 95.4 % ≈ 4.6 % ≈ 99 % ≈ 1 % ≈ 99.7 % ≈ 0.27 % ≈ 99.9 % ≈ 0.1 %
Слайд 24: Насколько высока надежность требования p<5%?
P n, p ( x )= C x n p x q n - x Нуль-гипотеза: выпадение герба четыре раза подряд является случайным P 4 ( x =4)=(1/2) 4 =1/16=0.0625=6.25%>5% - нуль-гипотеза не может быть отвергнута. Нуль-гипотеза: выпадение герба пять раз подряд является случайным P 5 ( x =5)=(1/2) 5 =1/32=0.03125=3.1%<5% - нуль-гипотеза д.б. отвергнута -появление герба пять раз – событие неслучайное
Слайд 25
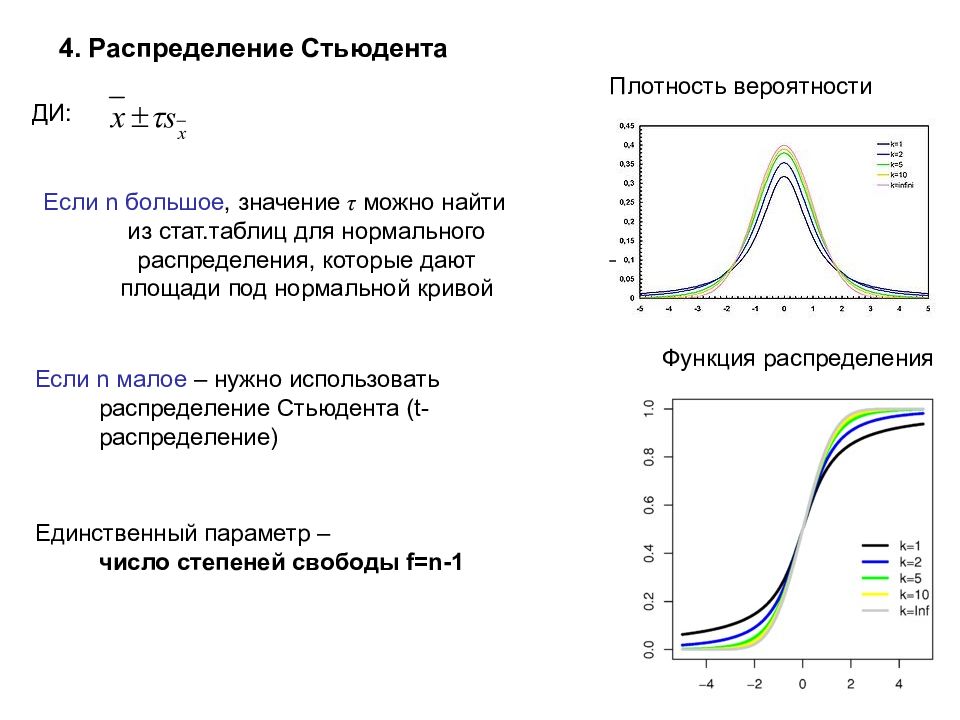
Плотность вероятности Функция распределения 4. Распределение Стьюдента Если n большое, значение τ можно найти из стат.таблиц для нормального распределения, которые дают площади под нормальной кривой ДИ: Если n малое – нужно использовать распределение Стьюдента ( t -распределение) Единственный параметр – число степеней свободы f=n-1
Слайд 26
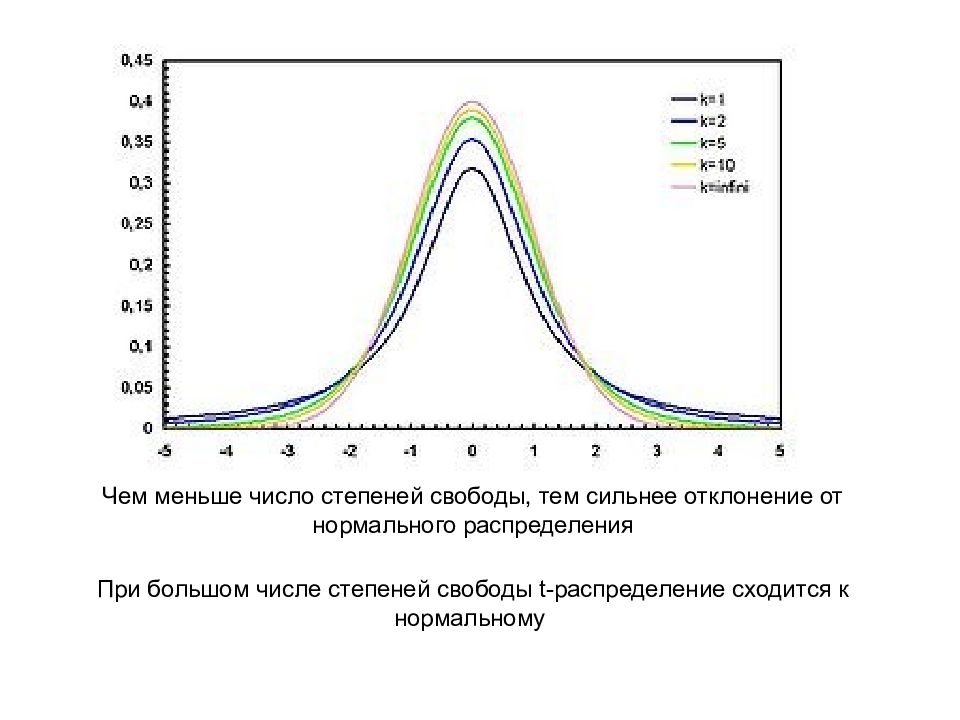
Чем меньше число степеней свободы, тем сильнее отклонение от нормального распределения При большом числе степеней свободы t -распределение сходится к нормальному
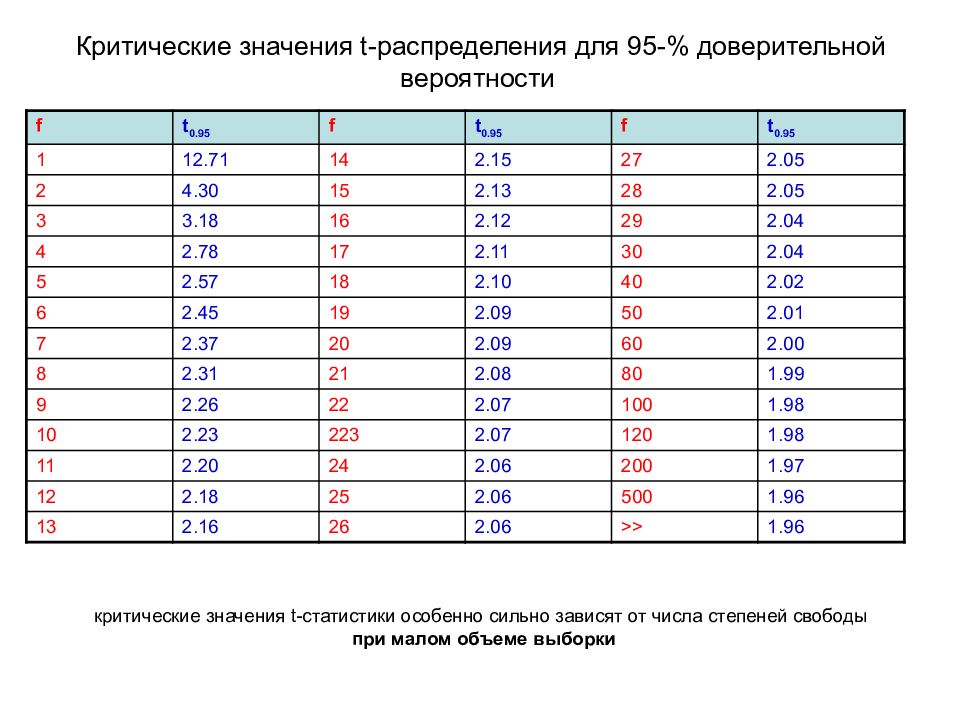
Слайд 27: Критические значения t -распределения для 95-% доверительной вероятности
f t 0.95 f t 0.95 f t 0.95 1 12.71 14 2.15 27 2.05 2 4.30 15 2.13 28 2.05 3 3.18 16 2.12 29 2.04 4 2.78 17 2.11 30 2.04 5 2.57 18 2.10 40 2.02 6 2.45 19 2.09 50 2.01 7 2.37 20 2.09 60 2.00 8 2.31 21 2.08 80 1.99 9 2.26 22 2.07 100 1.98 10 2.23 223 2.07 120 1.98 11 2.20 24 2.06 200 1.97 12 2.18 25 2.06 500 1.96 13 2.16 26 2.06 >> 1.96 критические значения t -статистики особенно сильно зависят от числа степеней свободы при малом объеме выборки