Первый слайд презентации
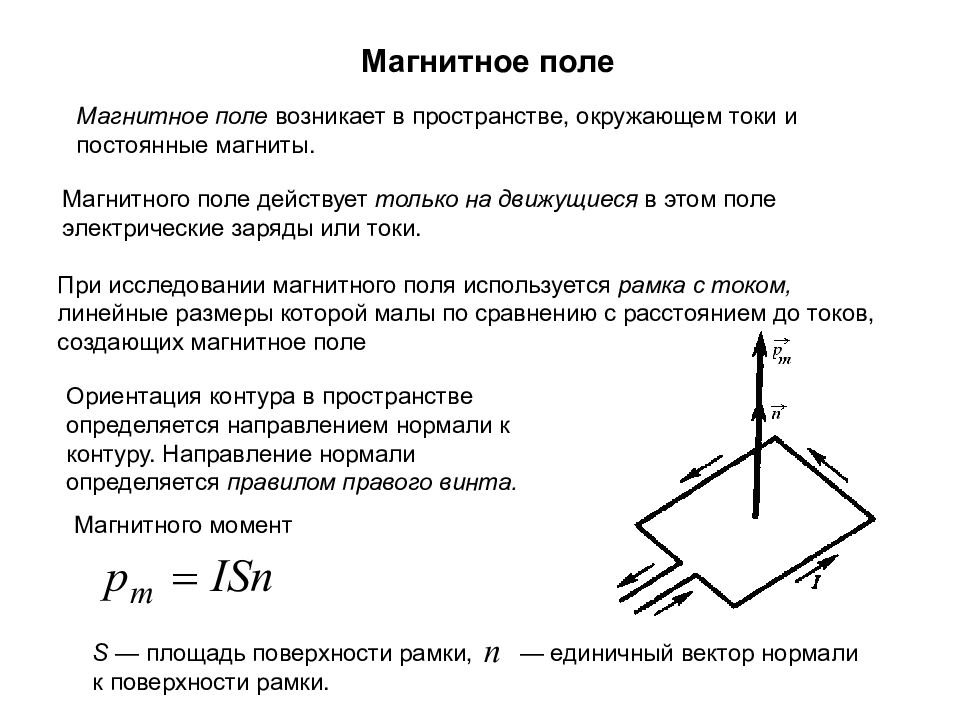
Магнитное поле Магнитное поле возникает в пространстве, окружающем токи и постоянные магниты. Магнитного поле действует только на движущиеся в этом поле электрические заряды или токи. При исследовании магнитного поля используется рамка с током, линейные размеры которой малы по сравнению с расстоянием до токов, создающих магнитное поле Ориентация контура в пространстве определяется направлением нормали к контуру. Направление нормали определяется правилом правого винта. Магнитного момент S — площадь поверхности рамки, — единичный вектор нормали к поверхности рамки.
Слайд 2
Магнитное поле оказывает на рамку с током ориентирующее действие. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к рамке Вращающий момент сил, действующий на рамку с током, зависит как от свойств поля в данной точке, так и от свойств рамки и определяется формулой Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Единица магнитной индукции — тесла
Слайд 4
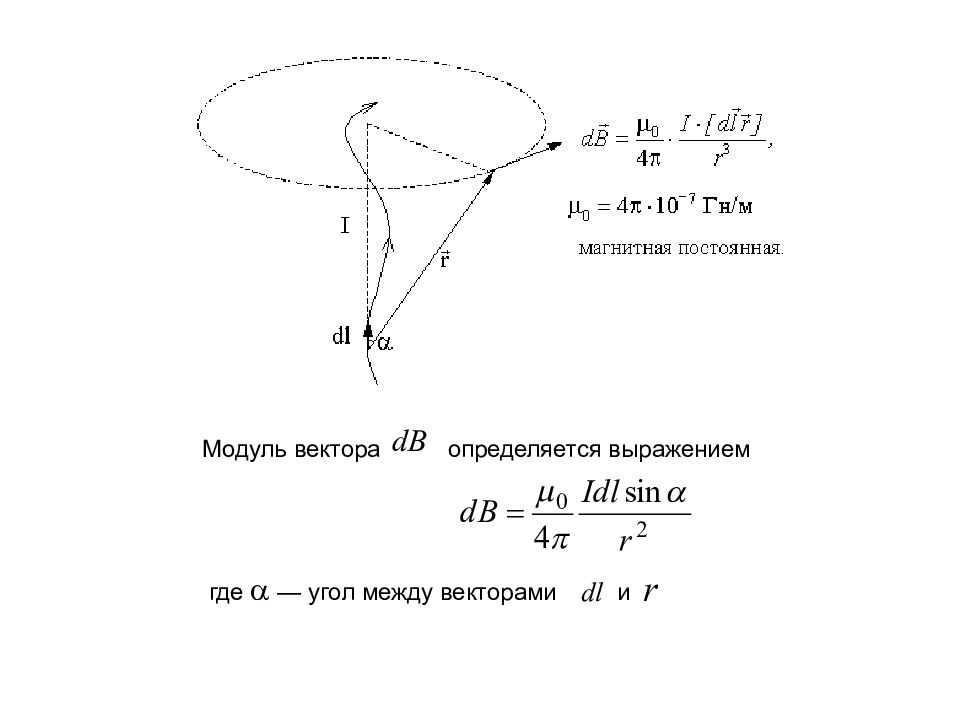
Закон Био - Савара – Лапласа Выражение для индукции магнитного поля создаваемого элементом этого проводника с током I в некоторой точке, записывается в виде где — вектор, по модулю равный длине элемента проводника dl и совпадающий по направлению с током, - радиус-вектор, проведенный из элемента проводника в точку поля, r — модуль радиуса-вектора - магнитная постоянная. Направление находится по правилу правого винта
Слайд 6
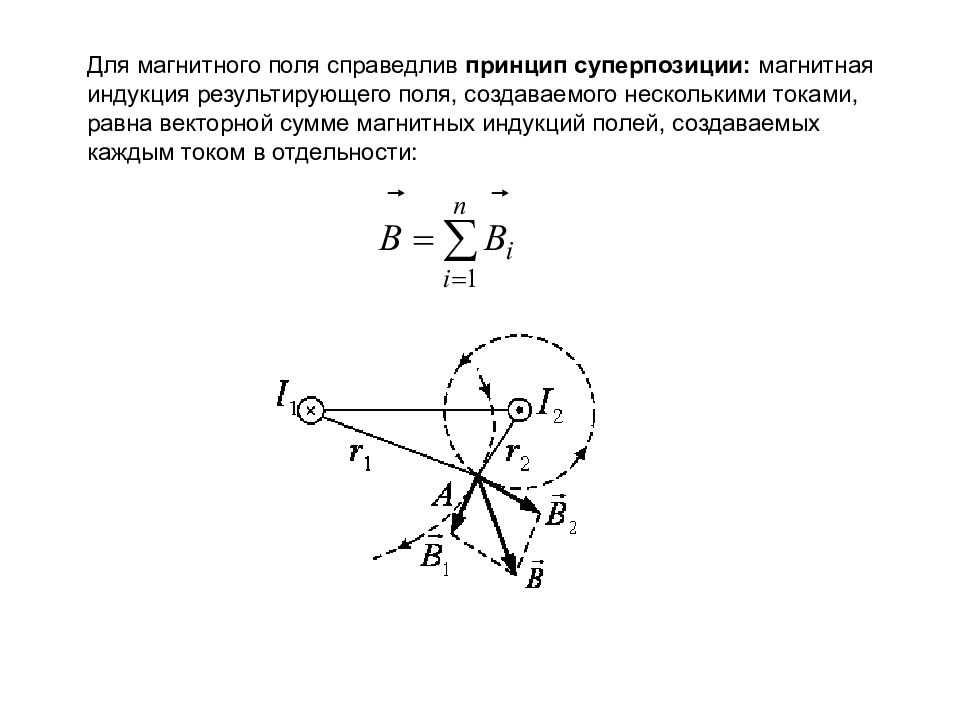
Для магнитного поля справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами, равна векторной сумме магнитных индукций полей, создаваемых каждым током в отдельности:
Слайд 7
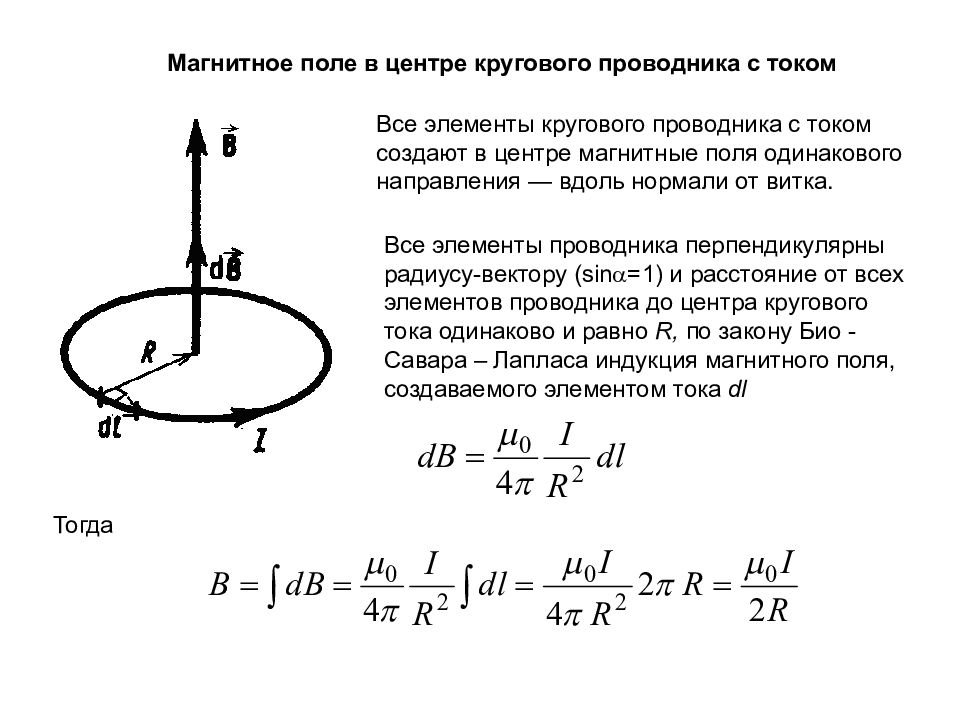
Магнитное поле в центре кругового проводника с током Все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Все элементы проводника перпендикулярны радиусу-вектору ( sin =1 ) и расстояние от всех элементов проводника до центра кругового тока одинаково и равно R, по закону Био - Савара – Лапласа индукция магнитного поля, создаваемого элементом тока dl Тогда
Слайд 8
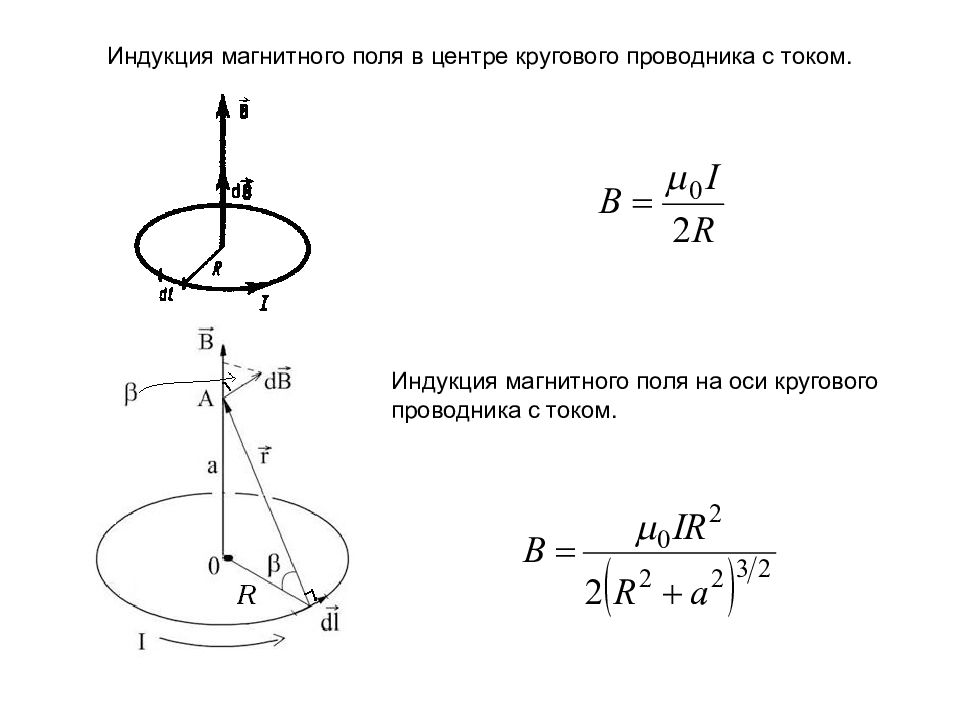
Индукция магнитного поля в центре кругового проводника с током. Индукция магнитного поля на оси кругового проводника с током.
Слайд 9
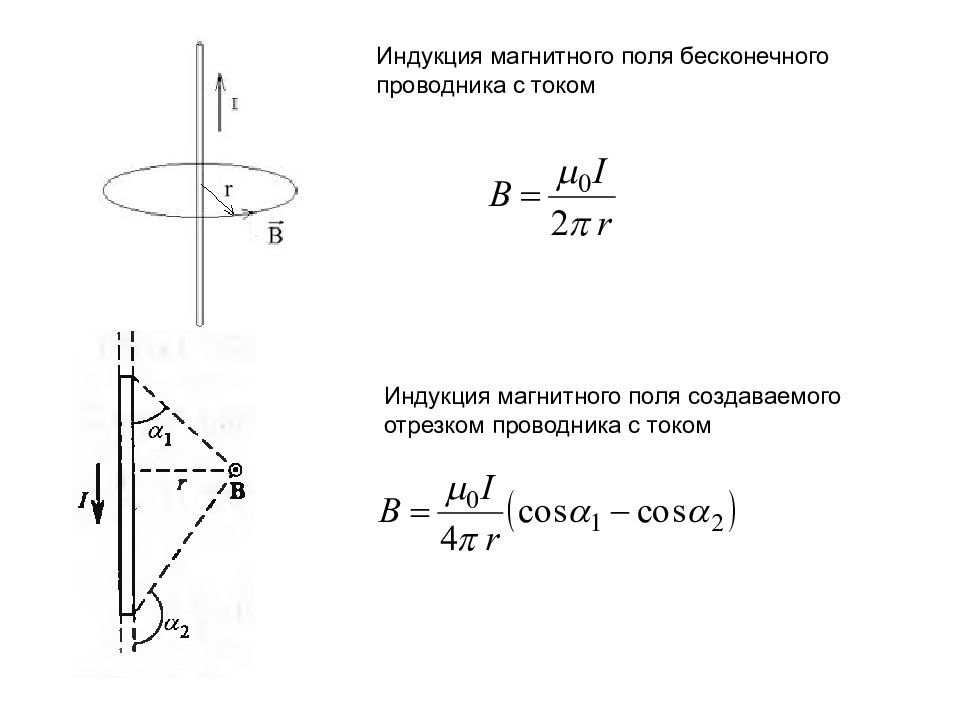
Индукция магнитного поля бесконечного проводника с током Индукция магнитного поля создаваемого отрезком проводника с током
Слайд 10
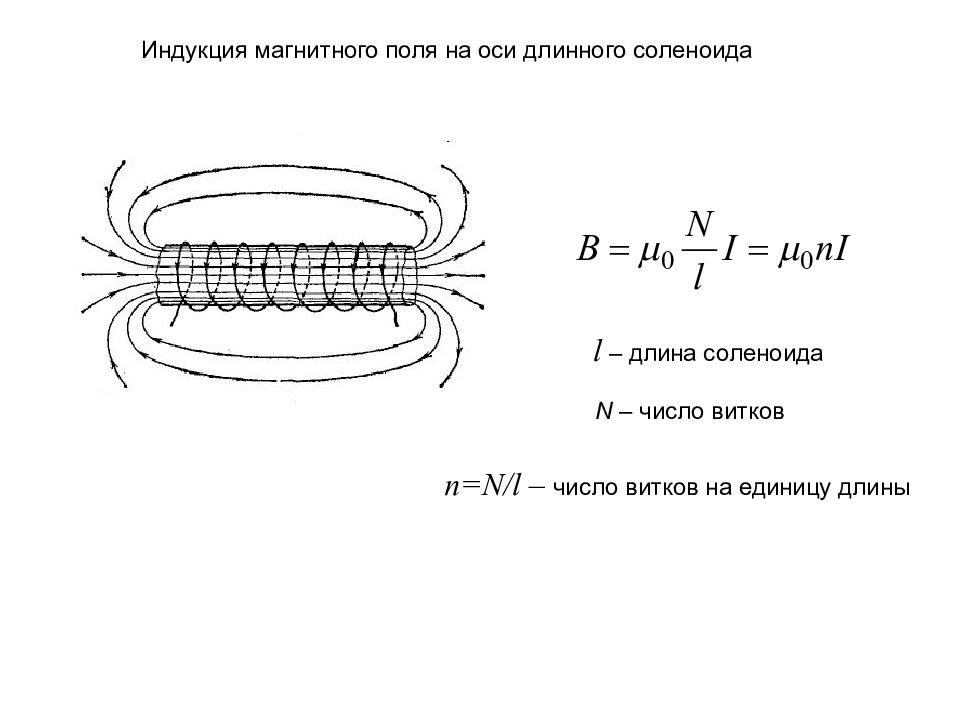
Индукция магнитного поля на оси длинного соленоида l – длина соленоида N – число витков n=N/l – число витков на единицу длины
Слайд 11
Циркуляция вектора индукции магнитного поля в вакууме Циркуляцией вектора по замкнутому контуру называется интеграл где - вектор элементарной длины контура, направленной вдоль обхода контура, — составляющая вектора в направлении касательной к контуру, — угол между векторами и. Теорема о циркуляции вектора B : Циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной 0 на алгебраическую сумму токов, охватываемых этим контуром: N — число проводников с токами, охватываемых контуром L произвольной формы.
Слайд 12
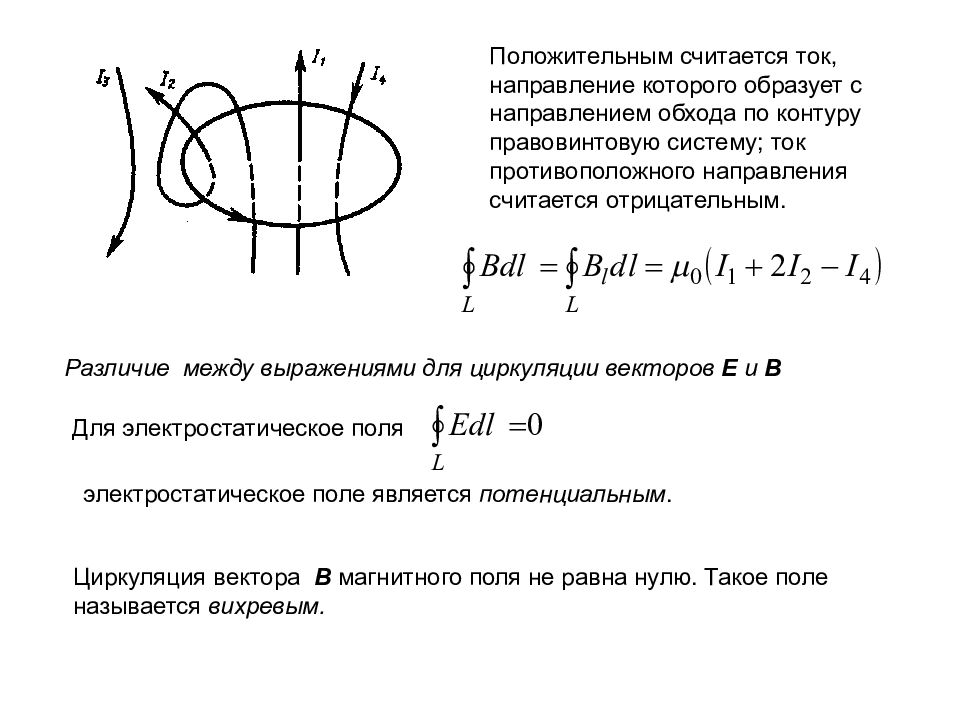
Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Различие между выражениями для циркуляции векторов E и B Для электростатическое поля электростатическое поле является потенциальным. Циркуляция вектора B магнитного поля не равна нулю. Такое поле называется вихревым.
Слайд 13
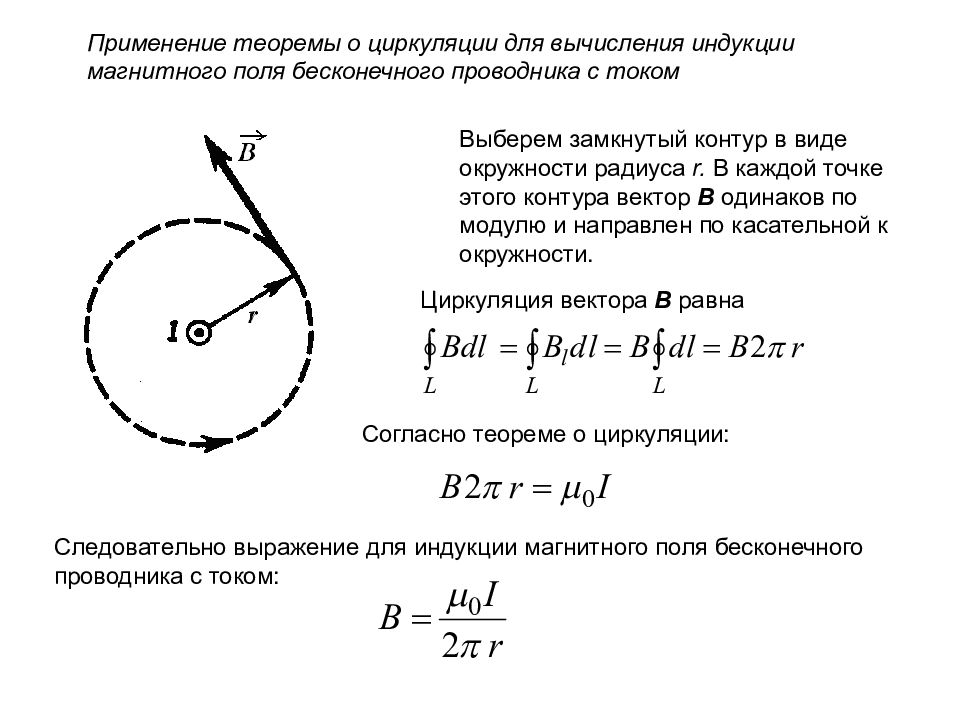
Применение теоремы о циркуляции для вычисления индукции магнитного поля бесконечного проводника с током Выберем замкнутый контур в виде окружности радиуса r. В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности. Циркуляция вектора В равна Согласно теореме о циркуляции: Следовательно выражение для индукции магнитного поля бесконечного проводника с током:
Слайд 14
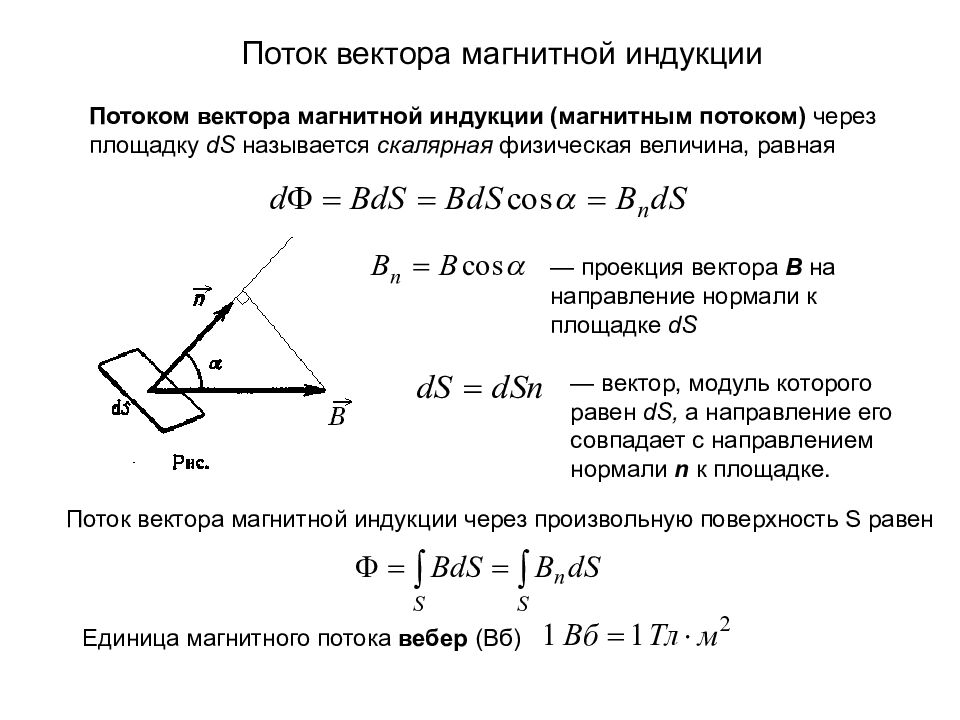
Поток вектора магнитной индукции Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная — проекция вектора B на направление нормали к площадке dS — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора магнитной индукции через произвольную поверхность S равен Единица магнитного потока вебер (Вб)
Слайд 15
Теорема Гаусса для поля B : поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции являются замкнутыми. Для сравнения: теорема Гаусса для вектора E Источником электростатического поля являются электрические заряды.
Слайд 16
Закон Ампера Сила с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, равна где dl - вектор, по модулю равный dl и совпадающий по направлению с током, B — вектор магнитной индукции. Сила Ампера
Слайд 17
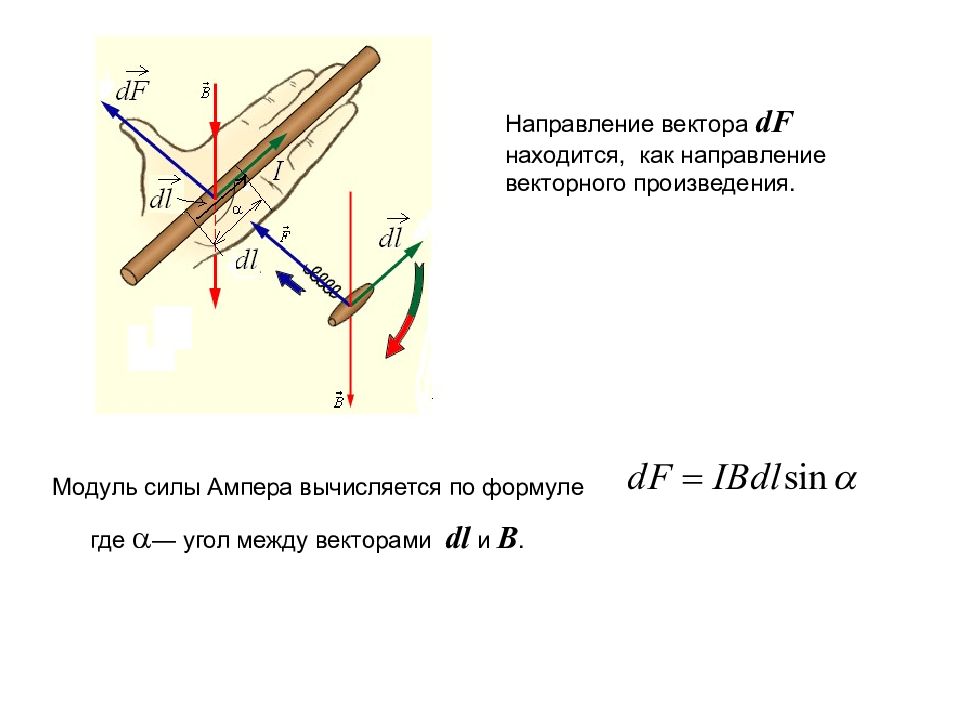
Направление вектора dF находится, как направление векторного произведения. Модуль силы Ампера вычисляется по формуле где — угол между векторами dl и B.
Слайд 18
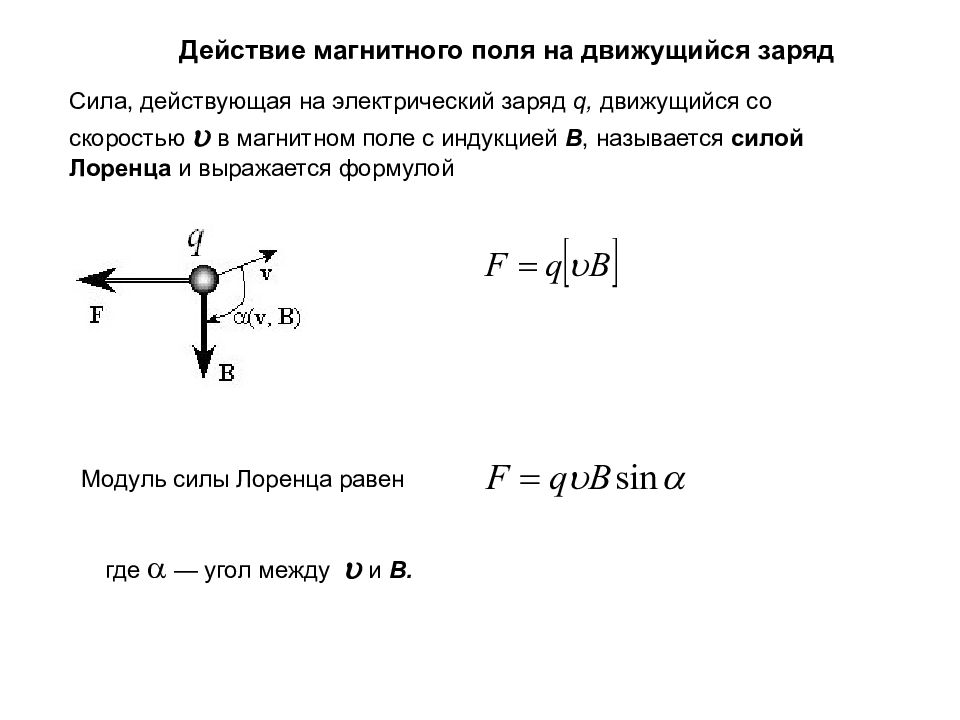
Действие магнитного поля на движущийся заряд Сила, действующая на электрический заряд q, движущийся со скоростью в магнитном поле c индукцией B, называется силой Лоренца и выражается формулой Модуль силы Лоренца равен где — угол между и B.
Слайд 19
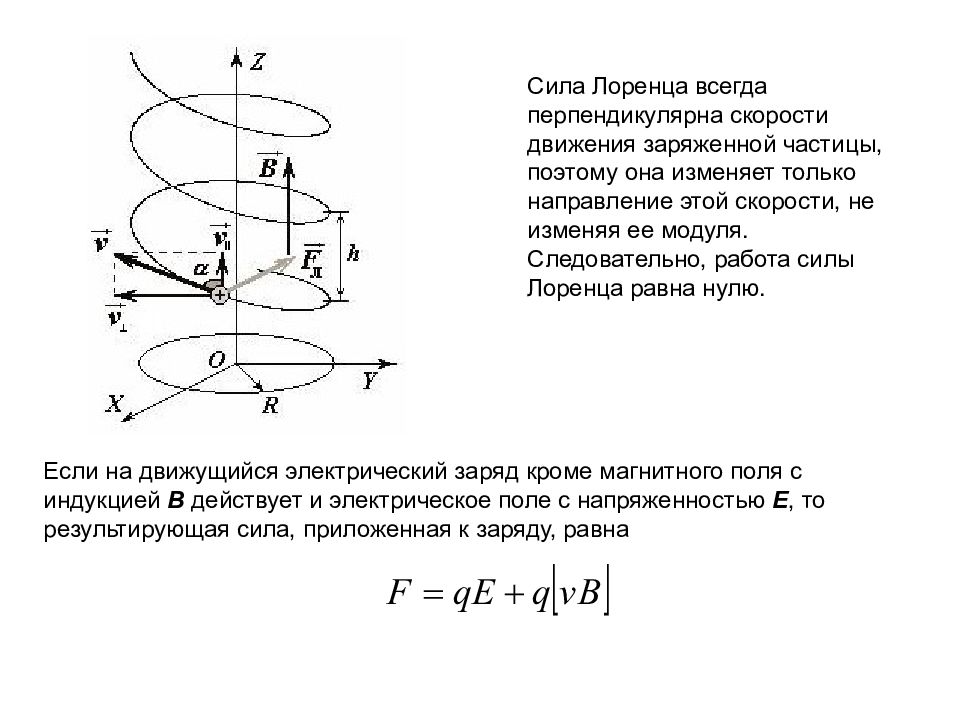
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, работа силы Лоренца равна нулю. Если на движущийся электрический заряд кроме магнитного поля с индукцией B действует и электрическое поле с напряженностью E, то результирующая сила, приложенная к заряду, равна
Слайд 20
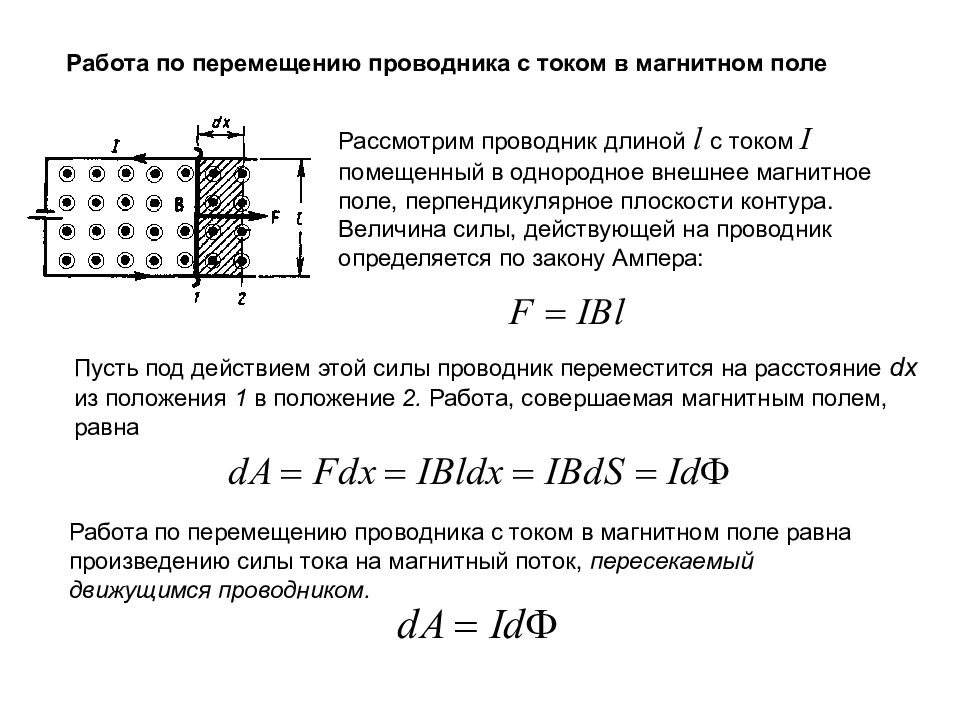
Работа по перемещению проводника с током в магнитном поле Рассмотрим проводник длиной l с током I помещенный в однородное внешнее магнитное поле, перпендикулярное плоскости контура. Величина силы, действующей на проводник определяется по закону Ампера: Пусть под действием этой силы проводник переместится на расстояние dx из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересекаемый движущимся проводником.
Слайд 21
Электромагнитная индукция В 1831 г. английский физик М. Фарадей, открыл явление электромагнитной индукции, которое заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного. Направление индукционного тока определяется правилом Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей Закон электромагнитной индукции Фарадея: какова бы ни была причина изменения магнитного потока, охватываемого замкнутым проводящим контуром, возникающая в контуре э. д. с. индукции численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Знак минус отражает правило Ленца
Слайд 22
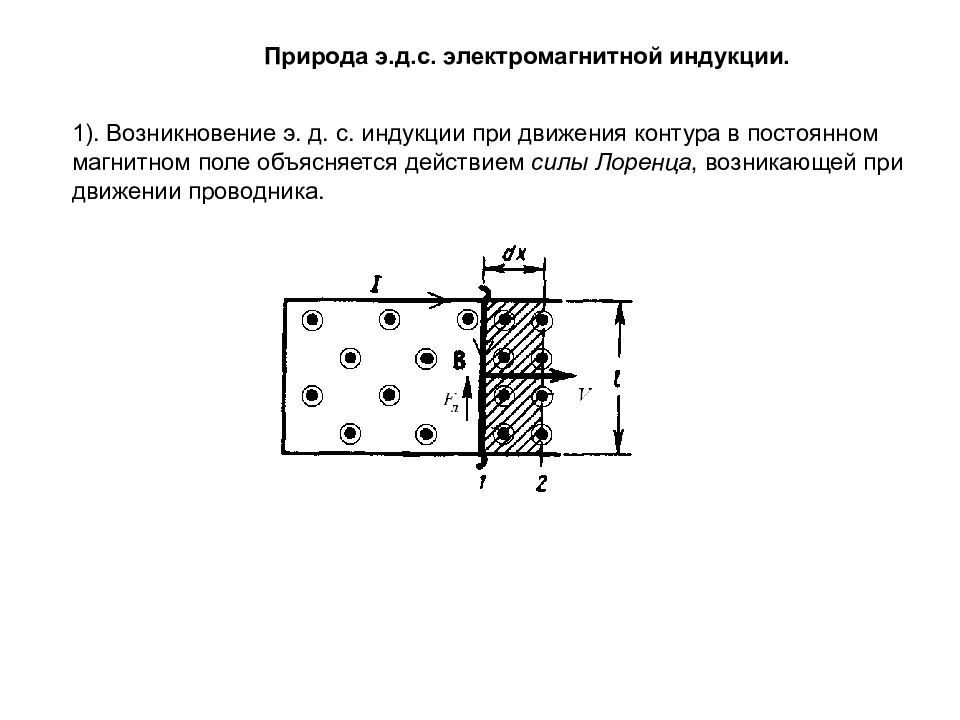
Природа э.д.с. электромагнитной индукции. 1). Возникновение э. д. с. индукции при движения контура в постоянном магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника.
Слайд 23
2). Для объяснения э. д. с. индукции в неподвижных проводниках Максвелл предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора E этого поля по любому неподвижному контуру L проводника представляет собой э. д. с. электромагнитной индукции: C другой стороны по закону Фарадея: Приравняв эти выражения получим: Циркуляция электрического поля, создаваемого изменяющимся магнитным полем отлична от нуля, значит, это поле не является потенциальным, а является как и магнитное поле вихревым.
Слайд 24
Индуктивность контура Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, пропорциональна току: Магнитный поток Следовательно Запишем в виде равенства Коэффициент пропорциональности L называется индуктивностью контура. Индуктивность зависит от геометрических размеров и формы контура, а также от магнитных свойств окружающей среды. Единицей индуктивности является генри (Гн). Индуктивностью 1Гн обладает контур, магнитный поток сквозь который при силе тока 1А равен 1Вб
Слайд 25
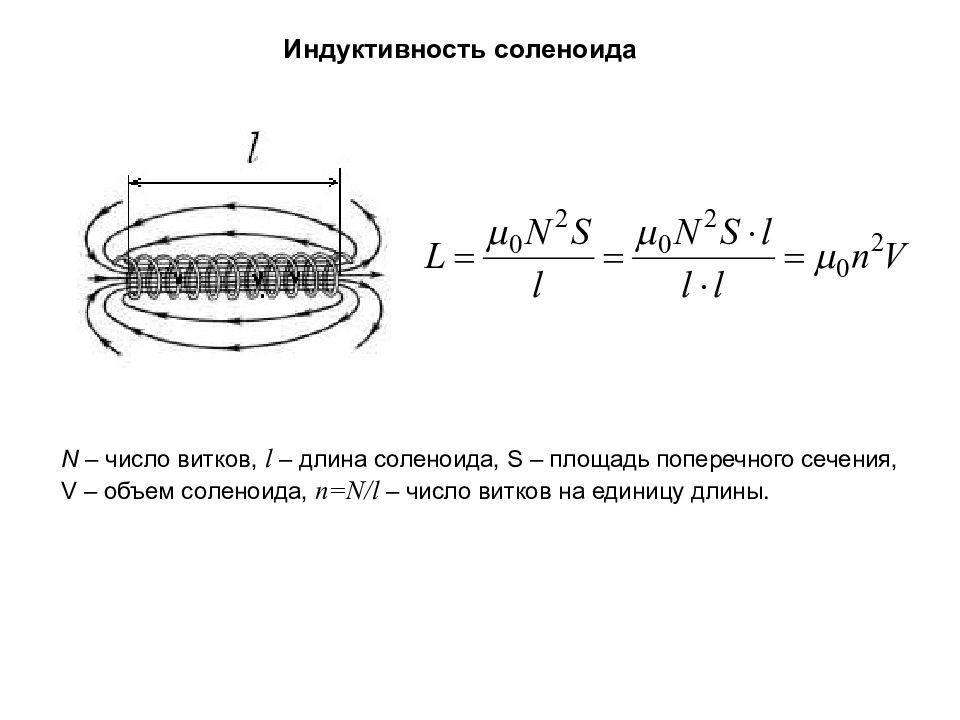
Индуктивность соленоида N – число витков, l – длина соленоида, S – площадь поперечного сечения, V – объем соленоида, n = N/l – число витков на единицу длины.
Слайд 26
Э.д.с. самоиндукции Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией. Для получения выражения для э.д.с. самоиндукции применим закон Фарадея: Если при изменении тока индуктивность L остается постоянной, то Знак минус показывает, что s всегда направлена так, чтобы препятствовать изменению силы тока
Слайд 27
Энергия магнитного поля Рассмотрим контур индуктивностью L, по которому течет ток I. Магнитный поток, создаваемый полем этого тока При изменении тока на dI, то магнитный поток изменяется на величину Для изменения магнитного потока на величину d необходимо совершить работу Работа по созданию магнитного потока будет равна Энергия магнитного поля, связанного с контуром, равна
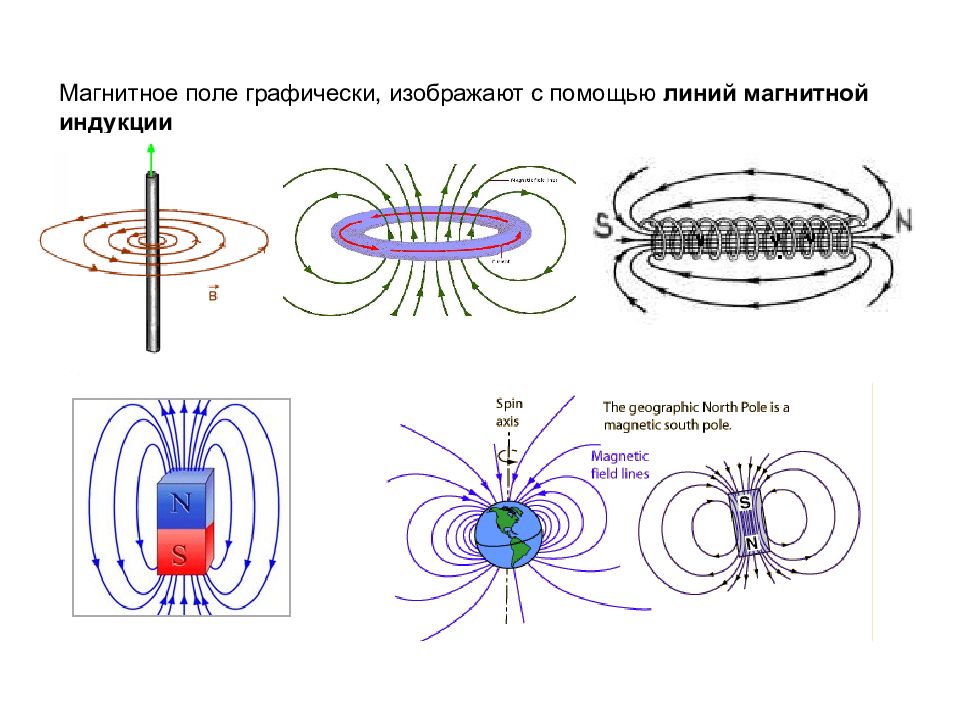
Последний слайд презентации: Магнитное поле Магнитное поле возникает в пространстве, окружающем токи и
Объемная плотность энергии магнитного поля - магнитная проницаемость среды. Объемная плотность энергии электрического поля E – напряженность электрического поля, - диэлектрическая проницаемость среды - электрическая постоянная