Слайд 2: 6.2.4. Энергия движения твёрдого тела
Согласно формуле скоростей твёрдого тела . Тогда полная кинетическая энергия т.т. может быть представлена следующим образом .
Слайд 3: Кинетическая энергия поступательного движения т.т
Первое слагаемое справа можно представить следующим образом . Оно представляет собой кинетическую энергию поступательного движения т.т.
Слайд 4: Второе слагаемое
Второе слагаемое преобразуем с учётом того факта, что для всех частиц т.т. одинаковыми являются скорости и, их можно вынести за знак суммы
Слайд 5: Для центра масс…
Под знаком суммы согласно определению радиус-вектора центра масс стоит произведение массы всего т.т. на радиус-вектор ц.м. Если в качестве начальной точки выбрать ц.м., то радиус-вектор ц.м. будет равен нулю. В этом случае нужно положить .
Слайд 6: Третье слагаемое
В третьем слагаемом снова вынесем угловую скорость за знак суммы, кроме того, учтём, что . Тогда . Это есть кинетическая энергия вращательного движения т.т.
Слайд 8: Полная энергия т.т
Таким образом, кинетическая энергия т.т. может быть представлена двумя слагаемыми . Это теорема Кёнига. А полная энергия – тремя .
Слайд 9: Закон изменения полной энергии т.т
Для движения т.т. справедлив закон изменения и сохранения полной энергии. Отличием от этих законов для материальной точки является только наличие дополнительного слагаемого – кинетической энергии вращательного движения т.т. .
Слайд 10: 6.3.Столкновение (удар) тел
Определение. Удар называется неупругим, если после удара тела движутся вместе. Расчёт неупругого удара основан на законе сохранения импульса: импульс тел д о удара равен импульсу тел после удара.
Слайд 11: Скорость тел после удара
Пусть – масса и скорость первого тела до удара, – масса и скорость второго тела до удара. Если удар неупругий, после удара тела будут двигаться вместе и скорость у них будет общая. Обозначим её просто Тогда
Слайд 12: Выделение тепла
При неупругом ударе кинетическая энергия тел не сохраняется, её часть переходит в тепло. Progr D: Progr E: Progr F: Progr G: Progr H:
Слайд 13: Кинетическая энергия относительного движения тел
Подставив в это выражение скорость после удара, найдём Таким образом, выделившееся тепло равно кинетической энергии относительного движения тел.
Слайд 14: Упругий удар
Определение. Упругим ударом называется удар, при котором сохраняется кинетическая энергия тел. Пусть снова – масса и скорость первого тела до удара, – масса и скорость второго тела до удара.
Если удар упругий тела после удара будут двигаться по-отдельности с разными скоростями. Поэтому закон сохранения импульса будет иметь вид: Однако для отыскания двух неизвестных нужно два уравнения. Второе – ЗСКЭ.
Слайд 16: Преобразование системы уравнений
В обоих уравнениях перенесём переменные с индексом 1 влево, с индексом 2 – вправо.
Слайд 17: Преобразование системы уравнений
Будем считать, что тела движутся вдоль одной прямой. Выберем эту прямую за ось ox и спроецируем на неё закон сохранения импульса:
Слайд 18: Преобразование системы уравнений
Вынесем массы за скобки, сократим во втором уравнении на 2 и разделим второе уравнение на первое, предварительно распишем разность квадратов на разность и сумму:
Слайд 19: Решение системы уравнений
Умножим теперь второе уравнение на массу первого тела и сложим с первым уравнением: Откуда и находим скорость второго тела после удара:
Слайд 20: Решение системы уравнений
Откуда и находим скорость второго тела после удара: Аналогично:
Слайд 21: Анализ решения
Если, то Тела меняются скоростями. В частности если скорость второго тела была равна нулю, то после удара остановится первый шар. Progr D: Progr E: Progr F: Progr G: Progr H :
Слайд 22: 7. Механика жидкостей и газов
7.1. Кинематика жидкостей и газов. Уравнение непрерывности. Определение. Жидкостью называется система материальных точек, взаимодействие которых таково, что частицы могут перемещаться друг относительно друга, но число частиц в единице объёма жидкости остаётся неизменным. Т.о. жидкость сохраняет свой объём, но не сохраняет своей формы. Она принимает форму сосуда, в который налита.
Слайд 23: Определение газов
Определение. Газом называется система материальных точек, взаимодействие между которыми не накладывает ограничений на взаимное перемещение частиц. Газы не сохраняют ни форму, ни объём.
Слайд 24: Давление
Для характеристики движения газов или жидкостей вводят понятие поля давлений и поля скоростей. Определение. Давлением внутри жидкости или газа называется физическая величина, численно равная силе, действующей на единицу площадки, расположенной перпендикулярно силе. Обозначается давление и по определению .
Слайд 25: Следствия из определения давления
1. Давление скалярная величина. 2. Размерность. Измеряется давление в единицах силы, делённых на единицу площади. Эта единица называется Паскаль. В общем случае давление зависит от времени и координат:.
Слайд 26: Поле давлений
Определение. Говорят, что в некотором пространстве задано поле давлений, если каждой точке этой области поставлено в соответствие число, равное давлению в этой точке.
Слайд 27: Поле скоростей
Определение. Говорят, что задано поле скоростей течения жидкости или газа, если каждой точке пространства поставлен в соответствие вектор скорости, указывающий быстроту и направление движения частиц жидкости или газа, находящихся в данной точке пространства. В общем случае поле скоростей зависит и от координат и от времени. .
Слайд 28: Состояние жидкости
Если поле скоростей не зависит от времени, оно называется стационарным. Течение в этом случае тоже называется стационарным. Если скорость течения жидкости во всех точках пространства равна нулю, состояние называется статическим.
Слайд 29: Линия тока
В процессе течения частицы жидкости или газа описывают некоторую кривую. Определение. Кривая, касательная в каждой точке к которой совпадает по направлению со скоростью течения жидкости или газа в этой точке, называется линией тока жидкости или газа. Для стационарного течения линия тока совпадают с траекториями движения частиц в данной точке.
Слайд 30: Трубка тока
Выберем в пространстве некоторый контур и через одну из его точек проведём линию тока. Заставим точку обежать весь контур. Пространство, заключённое внутри поверхности, описанной этой линией тока, называется трубкой тока, а сама поверхность называется стенкой трубки тока. Progr D: Progr E: Progr F: Progr G:
Слайд 31: Свойство стенки трубки тока
Стенка трубки характерна тем, что частицы, находящиеся на ней движутся по касательной к стенке и поэтому не могут её пересечь. Это значит, что зайти внутрь трубки тока или выйти из неё частицы могут только через основание трубки, но не через её стенки.
Слайд 32: Закон сохранения числа частиц в потоке
Отсюда следует, что в стационарном потоке количество частиц, заключённых внутри трубки тока между неподвижными её основаниями, будет оставаться с течением времени величиной постоянной. И наче говоря, сколько частиц внутрь трубки тока войдёт, столько за это же время из неё выйдет через другое основание. Это утверждение выражает закон сохранения числа частиц в потоке.
Слайд 34: Перемещение сечений трубки тока
Пусть за некоторое время частицы, находящиеся вблизи сечения, переместились на некоторое расстояние в новое положение вблизи сечения. За это же время частицы, находящиеся вблизи сечения, переместятся на некоторое расстояние в некоторое новое положение вблизи сечения.
Слайд 35: Число вошедших и вышедших частиц
Если концентрация частиц жидкости или газа вблизи сечения равна, число частиц, вошедших внутрь трубки тока, равно. Аналогично можно выразить число частиц, вышедших из трубки через сечение .
Слайд 36: Сохранение числа частиц
Согласно закону сохранения числа частиц количество вошедших и вышедших частиц должно быть одинаково, т.е. Разделим это равенство на общий промежуток времени .
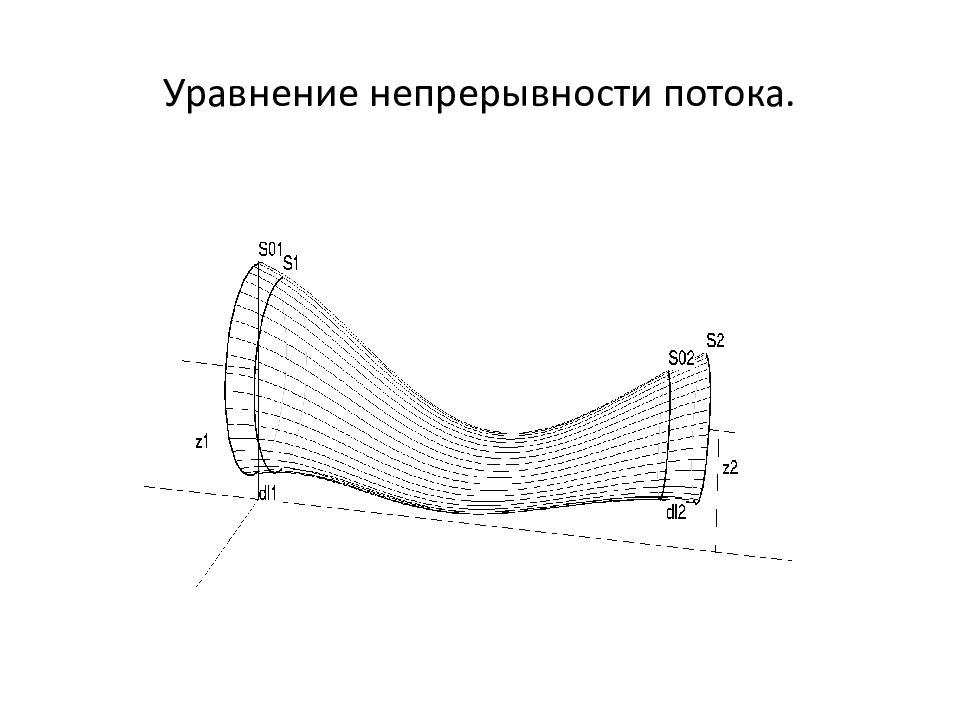
Слайд 37: Уравнение непрерывности
Но отношение пути, пройденного частицами за некоторый промежуток времени к этому промежутку, равно их скорости, так что можно записать . Это утверждение также выражает закон сохранения числа частиц, но в этом виде он называется уравнением непрерывности.
Слайд 38: Закон сохранения массы
Если массы частиц в потоке не меняются, то можно умножить закон сохранения частиц на массу одной частицы, тогда получится уравнение , которое тоже называется уравнением непрерывности, но выражает уже закон сохранения массы в потоке. Здесь и - плотности жидкости или газа в начале трубки тока и в конце соответственно.
Слайд 39: Уравнение непрерывности потока несжимаемой жидкости
Если жидкость несжимаема, то, и тогда уравнение непрерывности примет вид , Это утверждение называется уравнением непрерывности для несжимаемой жидкости и выражает закон сохранения объёма жидкости. Оно гласит: «Объём жидкости, втекающей внутрь трубки тока за единицу времени, равен объёму жидкости, вытекающей из трубки тока за единицу времени».
Слайд 41: Расход жидкости
Определение. Объём жидкости, протекающий через поперечное сечение трубки тока за единицу времени, называется расходом жидкости. Поэтому уравнение непрерывности для несжимаемой жидкости можно ещё прочитать так: «Расход несжимаемой жидкости вдоль трубки тока во всех её сечениях одинаков».
Слайд 42: 7.2. Динамика жидкости. Закон Бернулли
Пусть за некоторое время жидкость, находящаяся между сечениями и, сместится так, что сечение переместится на некоторое расстояние и займёт новое положение. Тем самым вне этого объёма жидкости окажутся все частицы, расположенные между сечениями и. В результате выделенная жидкость потеряет всю энергию, которой обладали частицы между сечениями и. Здесь аппликата середины сечения.
Слайд 43: Энергия, приобретённая жидкостью
За это же время сечения переместятся на некоторое расстояние в некоторое новое положение. Таким образом, выделенный нами объём жидкости приобретёт энергию частиц, находящихся меду сечениями и :
Слайд 44: Работа внешних сил
Согласно закону изменения полной энергии, разность между этими энергиями равна работе неконсервативных сил, действующих на частицы. Этими силами являются силы давления со стороны других слоёв жидкости. .
Слайд 45: Знак работы сил давления
. При этом работа сил давления вблизи первого сечения положительна, т.к. перемещение совпадает по направлению с силой, а работа сил давления вблизи второго сечения отрицательна, т.к. перемещение этого сечения противоположно силам.
Слайд 46: Закон изменения полной энергии для жидкости
Приравнивая изменение полной энергии к работе внешних сил, получим равенство: .
Слайд 47: Применимость равенства
Здесь необходимо отметить, что в балансе энергии не учитывалась тепловая энергия, связанная с изменением плотности жидкости. Поэтому данное уравнение справедливо только для несжимаемой жидкости и не справедливо для газа.
Слайд 48: Закон Бернулли
Поэтому положим в предыдущем равенстве . Кроме того, учтём, что для несжимаемой жидкости справедливо уравнение непрерывности, и тогда из закона изменения полной энергии получим . Это утверждение и носит название закона Бернулли.
Слайд 49: Формулировка закона Бернулли
Прежде, чем сформулировать это утверждение, заметим, что первое слагаемое справа есть плотность кинетической энергии жидкости, второе – плотность потенциальной энергии, а последнее есть давление внутри жидкости. И так, уравнение Бернулли гласит: «Сумма плотности кинетической, потенциальной энергии жидкости и давления внутри жидкости есть величина неизменная вдоль линии тока».
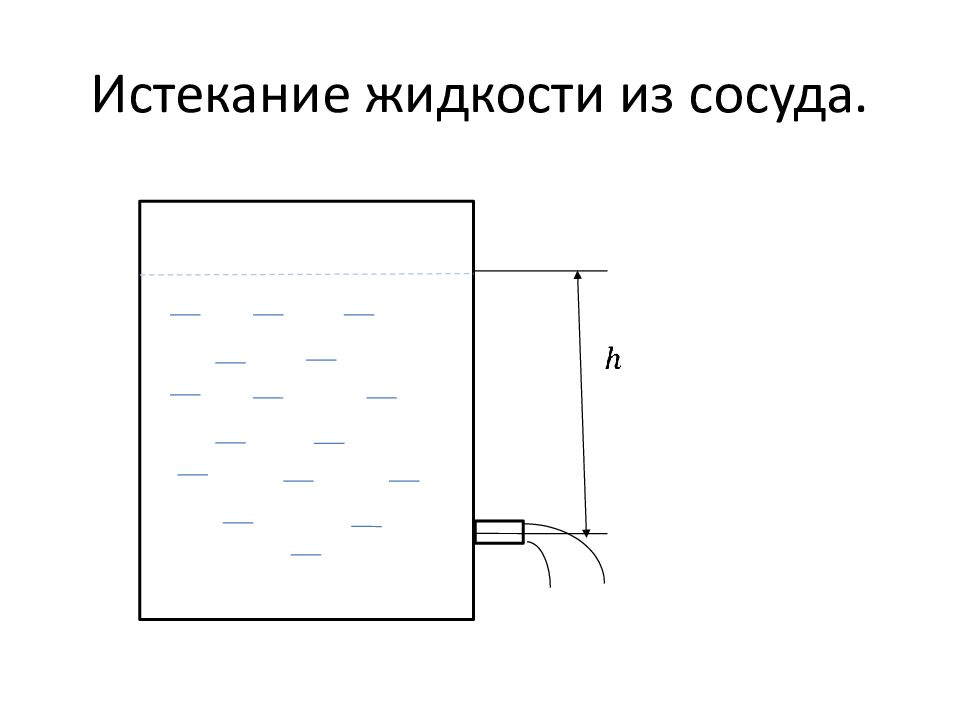
Слайд 51: Истекание воды из отверстия
Применим этот закон к явлению вытекания жидкости из отверстия в сосуде. Пусть высота жидкости в сосуд над отверстием, сечение отверстия в сосуде намного меньше площади сечения самого сосуда. Тогда согласно уравнению непрерывности скорость движения уровня в сосуде будет намного меньше скорости истечения из отверстия.
Слайд 52: Скоростью уровня жидкости пренебрегаем
Поэтому скоростью оп ускания уровня жидкости можно будет в уравнении Бернулли пренебречь. Если и верхняя часть сосуда и отверстие сообщаются с атмосферой, то давление на уровне жидкости в сосуде будет равно давлению в отверстии сосуда, т.е. .
Слайд 53: Уравнение Б ернулли для истекания жидкости
Индексом 1 обозначено давление над поверхностью воды, а 2 -в отверстии. Обозначим - скорость истечения жидкости. Тогда согласно закону Бернулли .
Слайд 54: Формула Торричелли
Т.к., то для скорости истечения окончательно получаем . Эта формула носит название формулы Торричелли. Она гласит: «Скорость истечения жидкости из малого отверстия в боковой стенке сосуда такая же, как если бы вода падала с высоты равной глубине отверстия».
Слайд 55: 7.3. Гидростатическое давление. Закон Архимеда. Условие плавания тел
Уравнение Бернулли применимо не только к движущейся, но также и к покоящейся жидкости. А именно, если скорость течения жидкости равна нулю, то уравнение Бернулли принимает вид. .
Слайд 56: Разность давлений на разных глубинах
Отсюда находим . Это означает, что разность давлений в двух точках покоящейся жидкости пропорциональна разности аппликат этих точек.
Слайд 57: Гидростатическое давление
В частности, если давление на уровне свободной поверхности жидкости равно атмосферному, а глубина погружения, то давление внутри жидкости на этой глубине будет определяться согласно формуле разности давлений следующим образом . Дополнительное давление, оказываемое столбом жидкости высотой, называется гидростатическим давлением .
Слайд 58: Силы, действующие на боковые грани куба в жидкости
Предположим, что внутрь жидкости помещено твёрдое тело в форме куба с ребром. На его стенки будет действовать гидростатическое давление. Но силы давления на боковые стенки будут компенсировать друг друга, т.к. боковые стенки находятся на одинаковой высоте и гидростатическое давление, оказываемое на них, будет одинаковым.
Слайд 59: Силы, действующие на основания
По-другому будет обстоять дело с верхней и нижней гранью. Они находятся на разных глубинах, и гидростатическое давление на них будет разным. Разными будут и силы давления на эти грани. Согласно формуле гидростатического давления разность давлений на нижнюю и верхнюю грани куба будет определяться длиной ребра куба .
Слайд 60: Выталкивающая сила
Чтобы найти разность сил, действующих на нижнюю и верхнюю грани, нужно умножить разность давлений на площадь этих граней .
Слайд 61: Сила Архимеда
Эта разность сил, очевидно, и будет сила, действующая на тело со стороны жидкости. Т.к. большая по модулю из сил и направлена вверх, то и результирующая сила со стороны жидкости на тело будет направлена вверх. Её и называют выталкивающей силой или силой Архимеда. Произведение есть, очевидно, объём тела, поэтому .
Слайд 62: Закон Архимеда
Это выражение и называется законом Архимеда. Он гласит: «Выталкивающая сила, действующая на тело со стороны жидкости, равна произведению плотности жидкости, ускорения свободного падения и объёма части тела, по г ружённой в жидкость и направлена в сторону противоположную ускорению свободного падения».
Слайд 63: Результирующая сила на тело в жидкости
На тело, погружённое в жидкость, кроме выталкивающей силы, действует ещё и сила тяжести. От соотношения этих двух сил и будет зависеть движение тела. А именно, проекция результирующей силы на вертикальную ось будет складываться из проекции выталкивающей силы и проекции силы тяжести. . Т.к., где - плотность тела, то .
Слайд 64: Условия плавания тел
Отсюда вытекает условие плавания тел. 1. Если, т.е. тело плотнее жидкости, то результирующая сила направлена вниз, и тело тонет. 2. Если, т.е. жидкость плотнее тела, то результирующая сила направлена вверх, и тело всплывает.
Слайд 65: Объём части тела под поверхностью жидкости
Но оно всплывает до тех пор, пока часть тела не окажется над жидкостью. В этом случае где - объём погружённой части тела, откуда и можно найти этот объём .
Слайд 66: Безразличное равновесие
3. И, наконец, если, т.е. плотность тела равна плотности жидкости, то результирующая сила, действующая на тело, равна нулю, и тело остаётся в жидкости в т.н. безразличном равновесии. Это означает, что тело может оставаться в покое в любой точке жидкости.
Слайд 67: 7.4. Внутреннее трение
Проведём мысленный эксперимент. По трубе течёт вода. Труба горизонтальна и одинакового сечения. Progr D: Progr E: Progr F: Progr G: Progr H : Согласно закону Бернулли давление во всех точках трубки должно быть одинаковым, а манометрические трубки показывают падение давления в сторону течения жидкости.
Слайд 68: Трение внутри жидкости
Это объясняется наличием трения слоёв жидкости друг о друга и о стенки трубы. Этим вопросом занимался Ньютон. Он пришёл к следующему закону. Progr D: Progr E: Progr F: Progr G: Progr H : . Это закон Ньютона. Здесь – площадь перекрытия слоёв, - разность скоростей движения слоёв, - разность аппликат слоёв.
Слайд 69: Коэффициент внутреннего трения
– коэффициент внутреннего трения. Он показывает, на сколько велика вязкость жидкости.
Слайд 70: Внутреннее трение между бесконечно близкими слоями
Если слои бесконечно близкие, то сила находится по закону: Воспользуемся этой формулой для определения расхода жидкости по трубе кругового сечения.
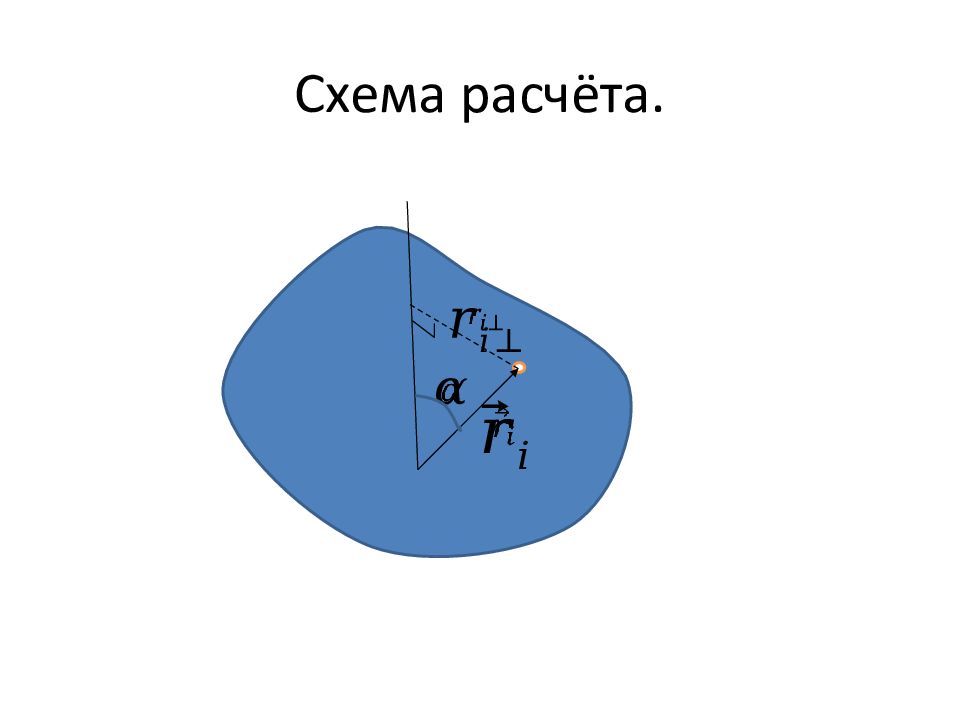
Слайд 71: Схема расчёта
Progr D: Progr E: Progr F: Progr G: Progr H: Если разность давлений по обе стороны трубы обозначить, то сила, проталкивающая жидкость сквозь выделенный цилиндр может быть найдена по формуле:
Слайд 72: Сила трения
С другой стороны сила трения, действующая на этот цилиндр равна:
Слайд 73: Баланс сил
Если течение стационарно, то эти две силы уравновешиваются: Откуда находим элемент скорости: и саму скорость:
Слайд 74: Начальные условия
Константа находится из начальных условий: на стенках трубы скорость частиц жидкости равна нулю: Откуда и находим константу:
Слайд 75: Поле скоростей
Подставим константу в формулу скорости: Это и есть формула поля скоростей по сечению трубы. Зависимость скорости от расстояния до центра трубы квадратична.
Слайд 76: Схема расчёта расхода
Progr D: Progr E: Progr F: Progr G: Progr H : Выделим бесконечно тонкий цилиндрический слой радиуса. За малое время через сечение этого слоя пройдёт малый объём жидкости Чтоб найти расход через всю трубу, нужно проинтегрировать.
Слайд 77: Формула Пуазейля
Разделим на время и найдём расход: Эта формула и носит название формулы Пуазейля
Слайд 78: Сила вязкого трения
Найдём силу, действующую на жидкость со стороны трубы. Для этого из формулы поля скоростей найдём скорость жидкости на оси трубы: Умножим и разделим на
Слайд 79: Сила трения жидкости о трубу
Очевидно есть сила трения, действующая со стороны стенок на жидкость. Так что Откуда Так находится сила трения жидкости о стенки трубы
Последний слайд презентации: Механика: Формула Стокса
Аналогично для движения шарика в вязкой среде Стоксом была найдена формула силы трения Она называется формулой Стокса. Эта формула строго применима только к телам шарообразной формы, но приближённо её можно применять и к другим телам, тогда вместо радиуса используется некоторый характерный размер тела.