Лектор: Парахин А.С., к. ф.-м. наук, доцент.
Пусть в некоторый момент времени положение материальной точки характеризовалось радиусом вектором, а в момент времени, радиусом вектором.
Определение. Вектор, соединяющий начальное и конечное положение материальной точки в течение промежутка времени называется её перемещением за этот промежуток времени. Как видно из определения, перемещение есть векторная величина, а длина перемещения измеряется в метрах. Этот факт записывают таким образом:
Так как любой вектор можно разложить по осям координат, перемещение также можно выразить через координаты радиуса вектора
Обозначим начальную точку А, а конечную В. Если промежуток времени устремить к нулю, точка В будет стремиться к точке А. В этом случае перемещение будет по направлению стремиться к единичному вектору касательной. Progr D: Progr E: Progr F: Progr G:
Progr E:
В физике элементом какой либо физической величины называется достаточно малое значение этой величины, т.е. значение, стремящееся к нулю. Т.е. величина, размерами которой можно пренебречь по сравнению с другими значениями этой величины в условиях данной задачи. Элементы физических величин обозначают обозначениями самой этой величины с добавлением латинской буквы d слева от обозначения величины. Таким образом, dt есть обозначение бесконечно малого промежутка времени, т.е. элементарного промежутка или элемента времени.
Если в качестве промежутка времени выбран элементарный, то перемещение за такой промежуток времени также будет элементарным. Его обозначают. Используя это понятие можно сказать, что элементарное перемещение параллельно вектору касательной, т.е.
Если обозначить - проекцию элементарного перемещения на направление касательной, то для элементарного перемещения можно записать .
Так как за достаточно малый промежуток времени точка движется в одну сторону, то элементарное изменение естественной координаты, модуль элементарного перемещения и модуль пути будут равны. Точнее говоря, они будут отличаться друг от друга на величины более высокого порядка малости, чем сами эти величины.
Для того чтобы охарактеризовать направление и быстроту перемещения материальной точки вводят понятие её скорости. Пусть за некоторый промежуток времени точка совершила перемещение. Определение. Средней скоростью движения называется величина, численно равная отношению перемещения за некоторый промежуток времени к величине этого промежутка.
Из определения следует. 1.Средняя скорость векторная величина. Направлена в сторону перемещения. 2. Размерность м/с.
Для более точного описания движения нужно знать мгновенную скорость. Определение. Мгновенной скоростью ил и просто скоростью движения материальной точки называется векторная величина, равная производной от радиуса вектора материальной точки по времени.
Таким образом, скорость материальной точки есть векторная величина. Она направлена по направлению элементарного перемещения, а элементарное перемещение – по касательной, значит, скорость направлена по касательной к траектории.
Таким образом, скорость материальной точки есть векторная величина. Как и любая другая векторная величина, скорость материальной точки соответствует трём скалярным величинам, а именно, её проекциям на оси координат
Из определения мгновенной скорости следует, что измеряется она в тех же единицах, что и средняя скорость, т.е.. Кроме этой системной единицы измерения скорости на практике часто используют несистемные единицы, самой распространённой из которых является. Чтобы перевести скорость из в, нужно умножить значение скорости на 3.6, при обратном переводе – разделить.
Так как скорость по направлению параллельна вектору касательной, её можно выразить через этот вектор . Здесь - проекция скорости на направление вектора касательной. Скорость и вектор касательной параллельны.
Модулем скорости называется абсолютная величина мгновенной скорости. . Модуль скорости может быть выражен и через координаты скорости
Равномерным называется движение, при котором скорость не меняется ни по направлению, ни по величине. Если скорость неизменна по направлению, движение прямолинейно. Если скорость неизменна по величине, движение называется равномерным по траектории.
Для того чтобы определить скорость, как функцию времени, нужно знать т.н. ускорение. Ускорение показывает величину и направление быстроты изменения скорости. Определение. Ускорением материальной точки называется векторная величина, равная производной от скорости материальной точки по времени.
1. Ускорение есть векторная величина. Его направление совпадает с направлением изменения скорости. 2. Размерность ускорения (единицы измерения)
,
Предположим, что точка движется по некоторой, в общем случае кривой, траектории. Обозначим - единичный вектор касательной. С его помощью вектор скорости можно выразить следующим образом: . Чтобы найти ускорение, нужно продифференцировать это выражение, как произведение двух функций. .
Отсюда видно, что ускорение в общем случае состоит из двух слагаемых. Первое слагаемое называется тангенциальным ускорением. Оно направлено по касательной, о чём говорит направление единичного вектора касательной. Если модуль скорости убывает, производная от касательной проекции скорости по времени отрицательна, и тангенциальное ускорение направлено против скорости, в противном случае - по вектору скорости.
По величине это слагаемое показывает, как быстро меняется касательная проекция скорости. Тангенциальное ускорение обозначают. Таким образом:
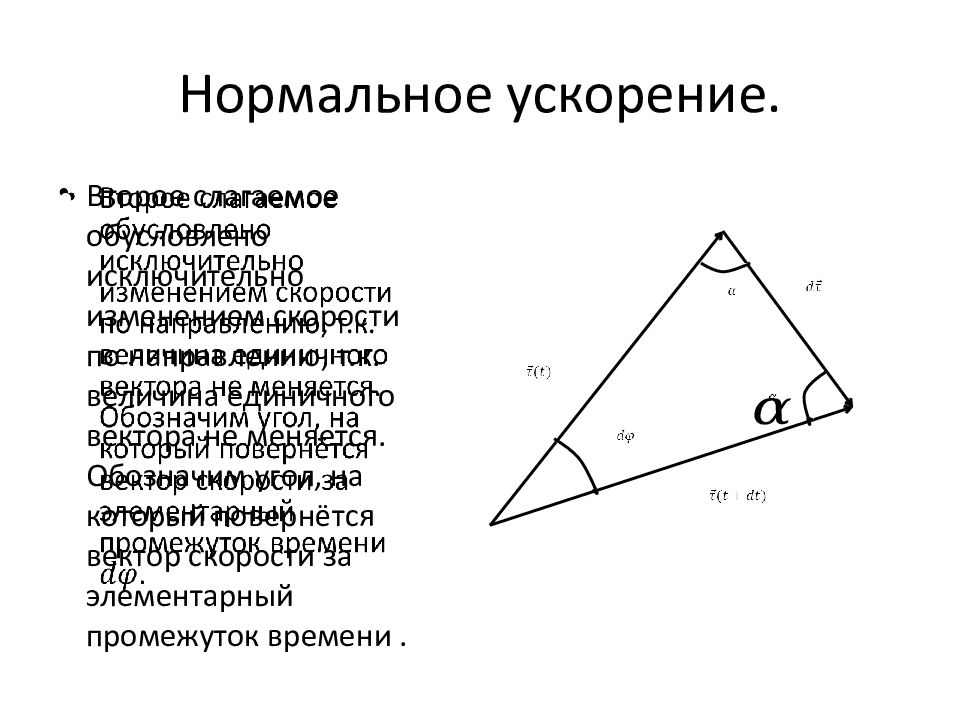
Второе слагаемое обусловлено исключительно изменением скорости по направлению, т.к. величина единичного вектора не меняется. Обозначим угол, на который повернётся вектор скорости за элементарный промежуток времени.
Тогда согласно теореме о суме внутренних углов треугольника Отсюда следует, что второе слагаемое направлено перпендикулярно траектории к центру кривизны. Поэтому это слагаемое называется нормальным ускорением.
Из треугольника также следует, что , а, где – радиус кривизны траектории. Тогда модуль второго слагаемого можно представить так: , а сам вектор в виде: , - единичный вектор нормали к траектории.
Полное ускорение представляется в виде суммы двух слагаемых . Так как тангенциальное и нормальное ускорение перпендикулярны, то полное ускорение по модулю можно найти с помощью теоремы Пифагора .
Если ускорение есть нуль, движение равномерное, если ускорение константа – движение равнопеременное, если тангенциальное ускорение нуль, движение равномерно по траектории, если константа – движение равнопеременное по траектории.
При этом если скорость и тангенциальное ускорение совпадают по направлению, скорость растёт, и движение называется ускоренным. Если скорость и тангенциальное ускорение противоположны, скорость убывает, и движение называется замедленным.
Если скорость материальной точки задана, как функция времени, то пользуясь определением скорости можно найти радиус-вектор, как функцию времени. А именно: В частном случае
Постоянная величина находится из так называемых начальных условий. Подставив это условие в закон движения, найдём постоянное слагаемое.Теперь эту константу подставим в закон равномерного движения и получим один из самых распространённых законов движения материальной точки. Закон равномерного движения.
Закон равномерного движения можно записать и в координатной форме
Если ускорение материальной точки задано, как функция времени, её скорость можно найти с помощью определения ускорения, а именно .
Если ускорение материальной точки есть величина постоянная, т.е. движение равнопеременное, интеграл в формуле скорости находится достаточно просто. Эта формула называется законом изменения скорости при равнопеременном движении.
Если скорость сонаправлена с ускорением, движение называется равноускоренным, в противном случае – равнозамедленным.
Константа вновь находится из начальных условий уже для скорости : Подставляя эти начальные условия в формулу скорости и определив константу, найдём закон изменения скорости
Закон изменения скорости можно записать в координатном виде:
Зная закон изменения скорости для равнопеременного движения, можно найти и закон этого движения, т.е. найти
Этот закон можно записать и в координатном виде
Одним из самых распространённых примеров равнопеременного движения является движение тела, брошенного под углом к горизонту, в частности, свободное падение тел. Если ось оу направить вдоль вертикали вверх, а ось ох по горизонтали (ось о z не понадобится), то в этом случае
Определение. Движение тела вблизи поверхности Земли только под действием силы тяжести называется свободным падением тел.
В частности, если тело падает с некоторой высоты, то. Выразив скорость падения, найдём
Примером переменного движения могут служить гармонические колебания. Progr D: Progr E: Progr F: Progr G: Определение. Периодическими движениями материальной точки называются такие движения, при которых она в каждую точку своей траектории постоянно возвращается через равные промежутки времени.
Определение. Промежуток времени, через который материальная точка возвращается в одну и ту же точку траектории при периодическом движении, называется периодом движения. Обозначается и измеряется в секундах.
Определение. Механическими колебаниями материальной точки называются такие периодические движения материальной точки между двумя крайними точками пространства, при которых траектория движения материальной точки в одну сторону совпадает с траекторией движения в другую сторону.
Определение. Гармоническими колебаниями называются такие колебания, законы которых имеют вид или
Если колебание происходит вдоль оси, закон движения может быть записан в скалярной форме Определение. Положение колеблющейся материальной точки, при котором, называется положением равновесия. Величина называется амплитудой колебания и показывает, каково максимальное отклонение колеблющейся материальной точки от положения равновесия.
Величина называется фазовым множителем, он показывает, какую часть от максимального значения составляет в данный момент времени координата колеблющейся материальной точки. Величина называется фазой колебания и определяет, в какой стадии колебания находится колеблющееся тело. Измеряется в радианах.
Величина называется круговой частотой и определяет скорость изменения фазы колебания. Чем больше круговая частота, тем быстрее совершаются колебания. Между круговой частотой и периодом существует связь. За один период фаза должна измениться на, так что
Определение. Циклической частотой называется величина, численно равная количеству полных циклов колебаний за единицу времени. Обозначается и равна так что
