Первый слайд презентации: Метод анализа иерархий
Идея метода состоит в структуризации путем построения многоуровневой иерархии, объединяющей все представляющие интерес компоненты, которые далее сравниваются между собой с помощью специально разработанных для этого процедур. В результате становится возможным получение численных оценок интенсивности взаимовлияния элементов иерархии, на основе которых оцениваются степени предпочтительности альтернатив относительно главной цели.
Слайд 3
Характеристика метода анализа иерархий (МАИ) Многокритериальный метод, в основе которого положена аддитивная свертка частных критериев в обобщенный критерий; Субъективный метод, так как численные значения частных критериев и их весов формируются на основе балльной оценки парных предпочтений лица принимающего решение(ЛПР); Относится к методам деревьев целей благодаря иерархической последовательности формирования обобщенного критерия оценки на основе частных критериев.
структурирование проблемы выбора в виде иерархии или сети; установка приоритетов критериев и оценка каждой из альтернатив по критериям; вычисляются коэффициенты важности для элементов каждого уровня. При этом проверяется согласованность суждений; подсчитывается комбинированный весовой коэффициент и определяется наилучшая альтернатива.
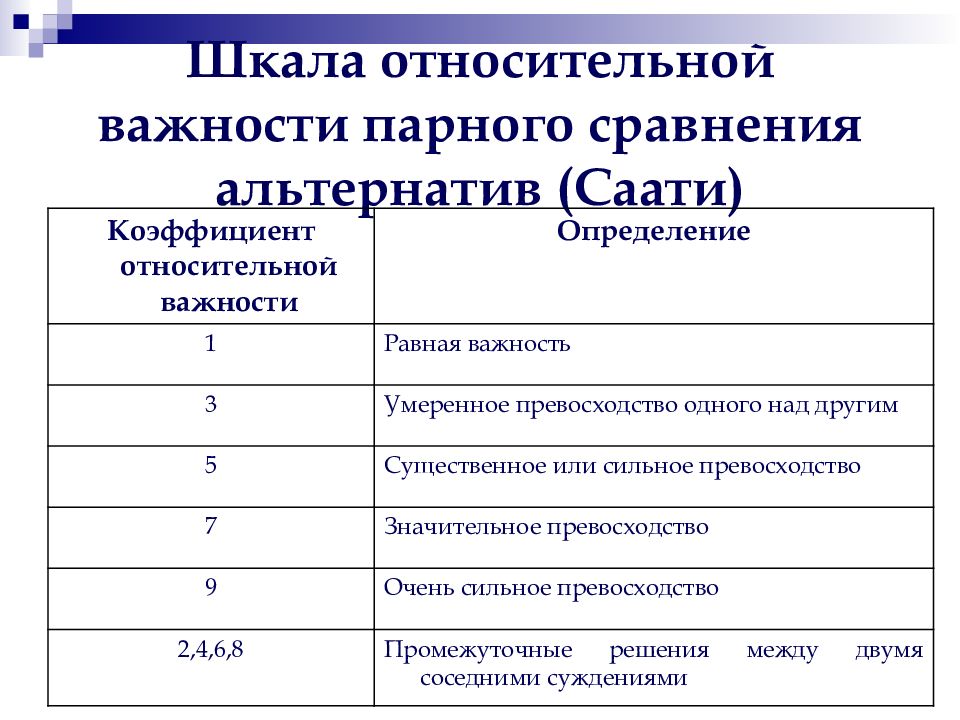
Коэффициент относительной важности Определение 1 Равная важность 3 Умеренное превосходство одного над другим 5 Существенное или сильное превосходство 7 Значительное превосходство 9 Очень сильное превосходство 2,4,6,8 Промежуточные решения между двумя соседними суждениями
Слайд 6
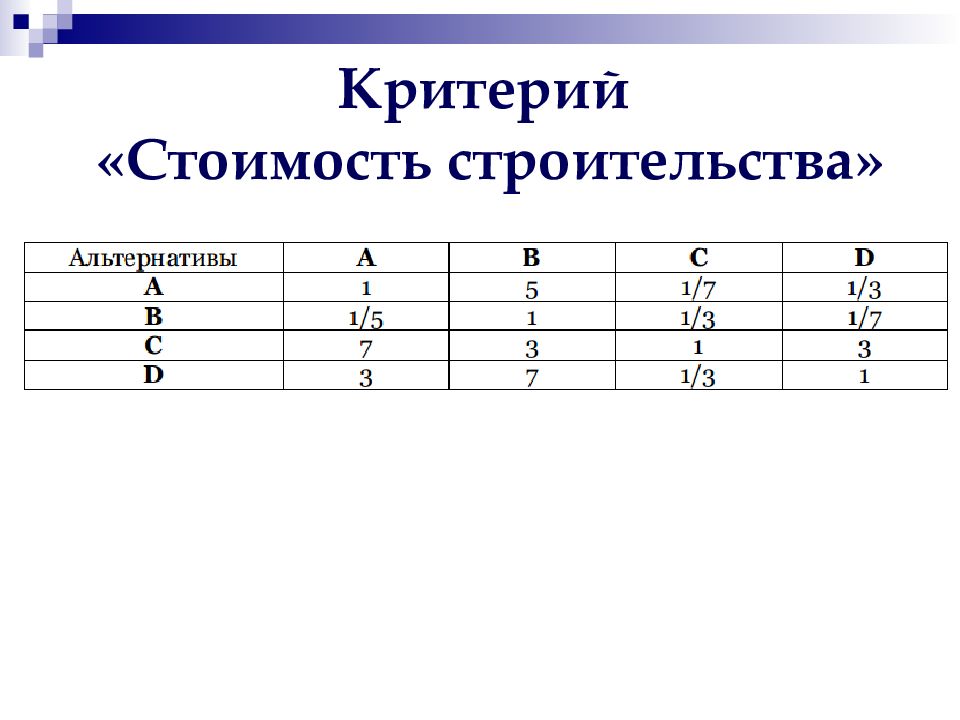
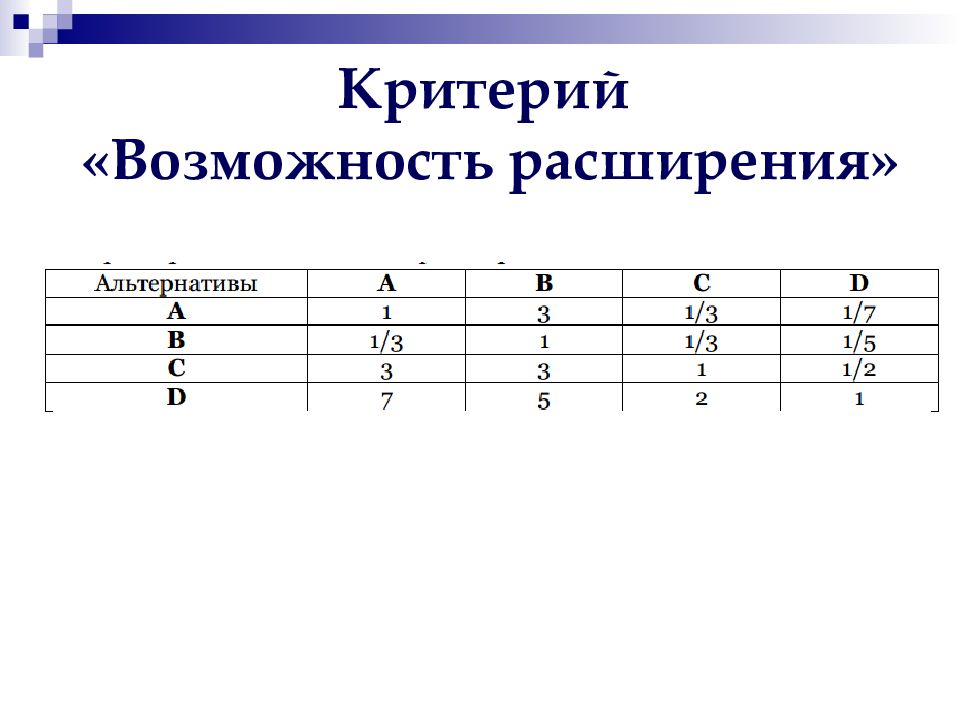
Пример 1. Компания, занимающаяся поставкой запасных частей для грузоподъемной техники, работающей в морском торговом порту, принимает решение открыть новое торговое представительство в одном из районов города. Городские власти предлагают под строительство четыре земельных участка: А, В, С и D. Критерии при выборе места строительства следующие: - место расположения – K1; - стоимость строительства – K2; - возможность дальнейшего расширения– K3.
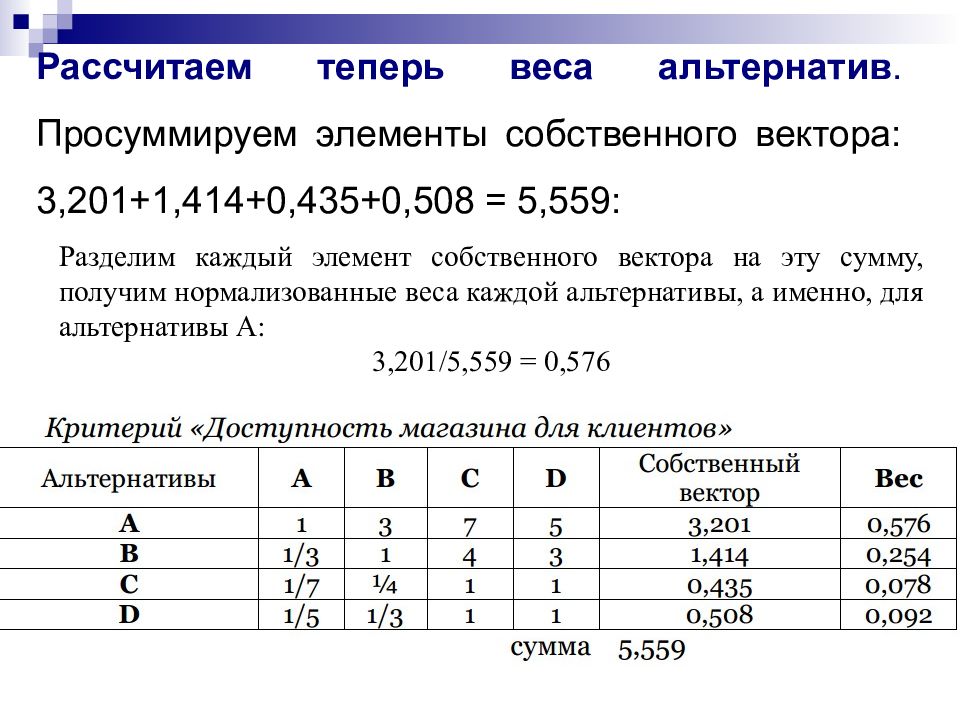
Слайд 7: Критерий «Доступность магазина для клиентов»
ЛПР, сравнил альтернативы и решил, что А по сравнению с В имеет умеренное преимущество (балл 3), А по сравнению с С имеет значительное превосходство (балл 7) и А по сравнению с D – существенное превосходство (балл 5).
Слайд 10
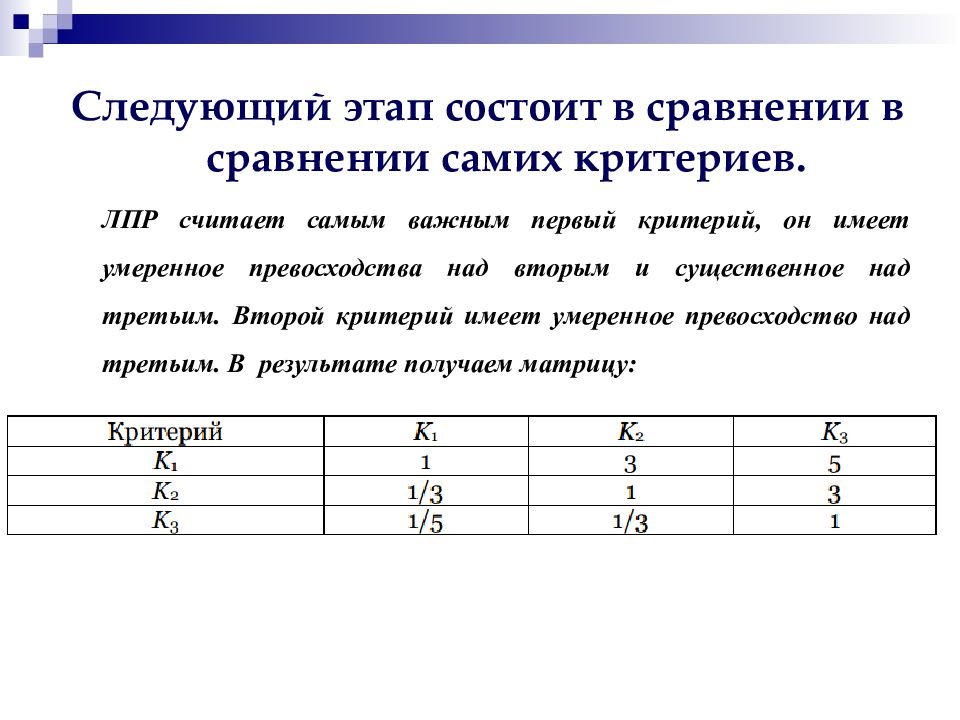
Следующий этап состоит в сравнении в сравнении самих критериев. ЛПР считает самым важным первый критерий, он имеет умеренное превосходства над вторым и существенное над третьим. Второй критерий имеет умеренное превосходство над третьим. В результате получаем матрицу:
Слайд 11: Далее вычисляются собственные векторы альтернатив по всем критериям
Для каждой i-й альтернативы по k-му критерию вычисляем элемент вектора, который равен среднегеометрическому показателей матрицы сравнения для этой альтернативы (строки матрицы):
Слайд 12: Расчет собственных векторов и весов альтернатив по каждому критерию
Для первого критерия «Доступность магазина для клиентов» собственный вектор альтернативы А равен:
Слайд 14: Рассчитаем теперь веса альтернатив. Просуммируем элементы собственного вектора: 3,201+1,414+0,435+0,508 = 5,559:
Разделим каждый элемент собственного вектора на эту сумму, получим нормализованные веса каждой альтернативы, а именно, для альтернативы А: 3,201 /5,559 = 0,576
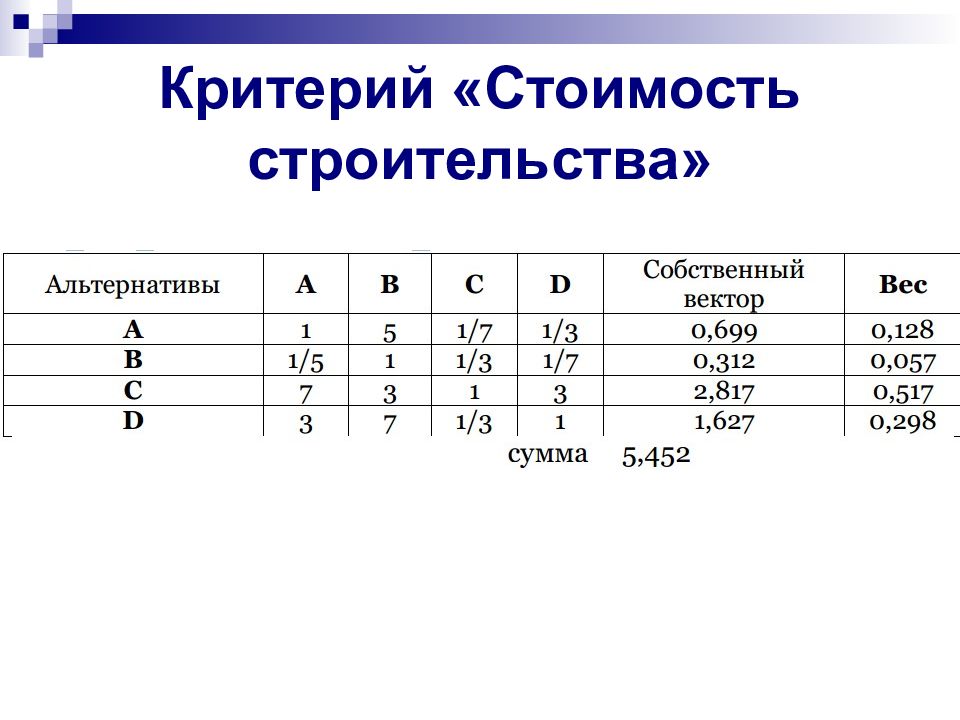
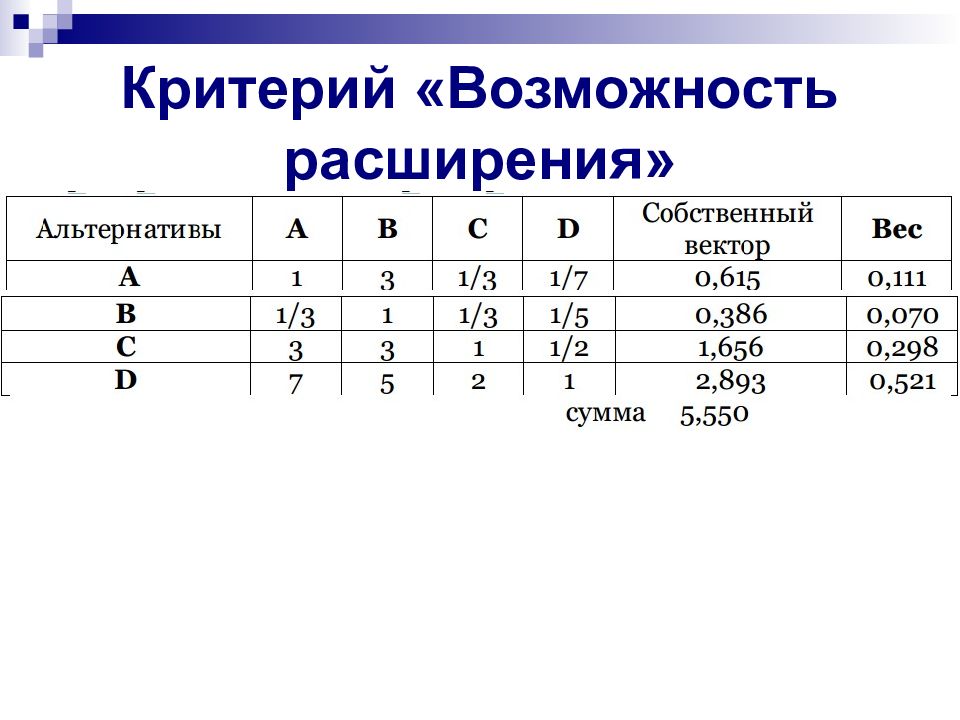
Слайд 17: Далее в результате нормализации собственных векторов вычисляют веса альтернатив по каждому критерию и веса самих критериев
Вес i-й альтернативы по k-му критерию равен отношению соответствующего элемента собственного вектора к сумме всех элементов собственного вектора данного критерия: