Первый слайд презентации: Методика обучения младших школьников решению задач на движение
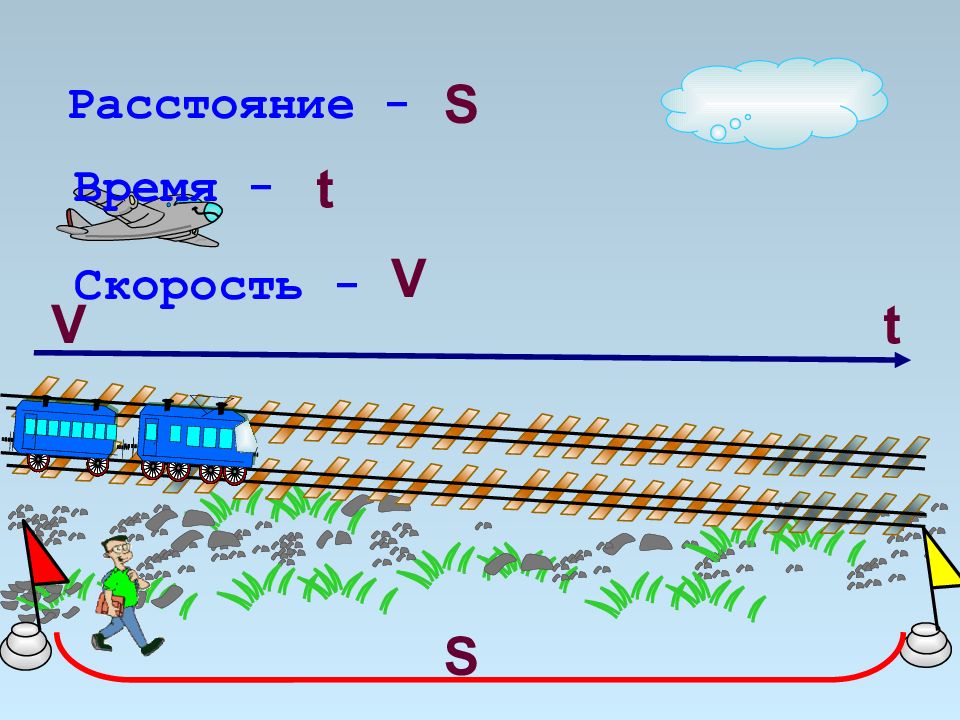
Слайд 2: Скорость (V)
Скоростью - называется расстояние, пройденное в единицу времени (за какое-то время – час, минуту, секунду). Обозначение - V Единицы измерения: км/ч, м/с, км/м, …
Слайд 3: Время (t)
Время – процесс смены явлений, вещей, событий. Обозначение - t Единицы измерения: мин, сек, ч, сутки.
Слайд 4: Расстояние (s)
Расстояние - это пространство разделяющее два пункта; промежуток между чем-либо. Обозначение - S Единицы измерения: мм, см, м, км, шаги
Слайд 5
Цель – осмысление понятий «скорость», «время», «расстояние», осознание зависимости между скоростью, временем, расстоянием. 1 этап
Слайд 7
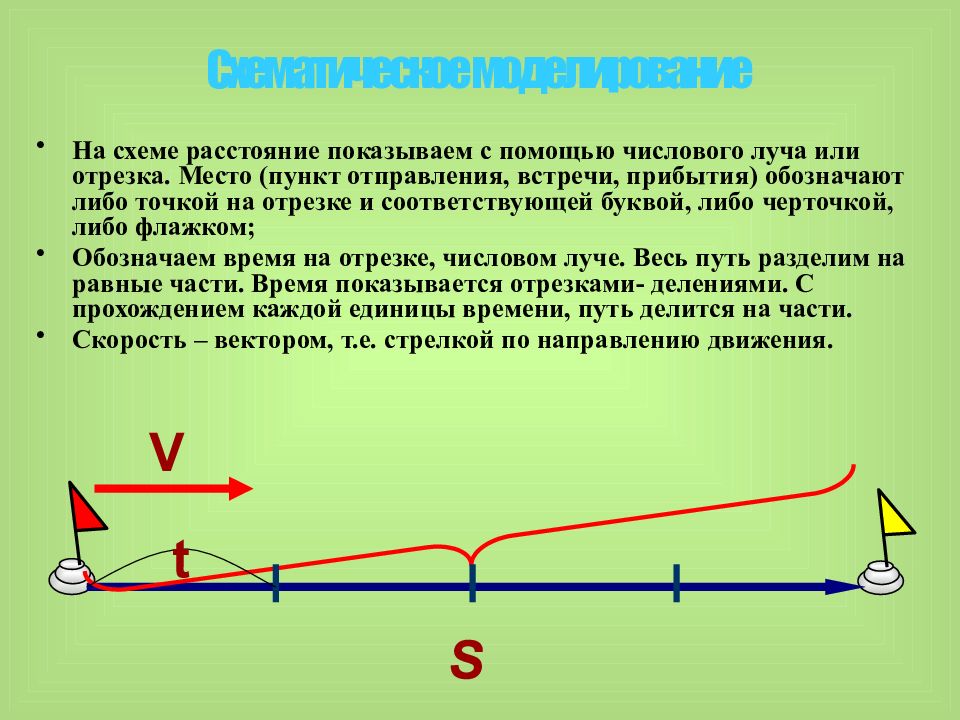
На схеме расстояние показываем с помощью числового луча или отрезка. Место (пункт отправления, встречи, прибытия) обозначают либо точкой на отрезке и соответствующей буквой, либо черточкой, либо флажком; Обозначаем время на отрезке, числовом луче. Весь путь разделим на равные части. Время показывается отрезками- делениями. С прохождением каждой единицы времени, путь делится на части. Скорость – вектором, т.е. стрелкой по направлению движения. S t V Схематическое моделирование
Слайд 8
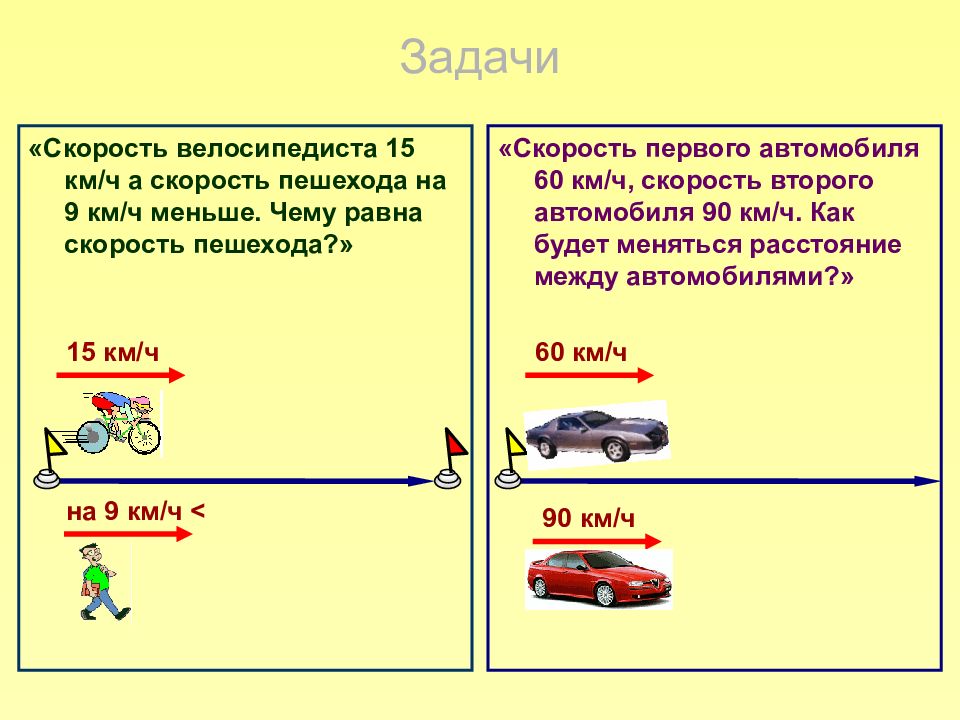
«Скорость велосипедиста 15 км/ч а скорость пешехода на 9 км/ч меньше. Чему равна скорость пешехода?» «Скорость первого автомобиля 60 км/ч, скорость второго автомобиля 90 км/ч. Как будет меняться расстояние между автомобилями?» 15 км/ч на 9 км/ч < 90 км/ч 60 км/ч Задачи
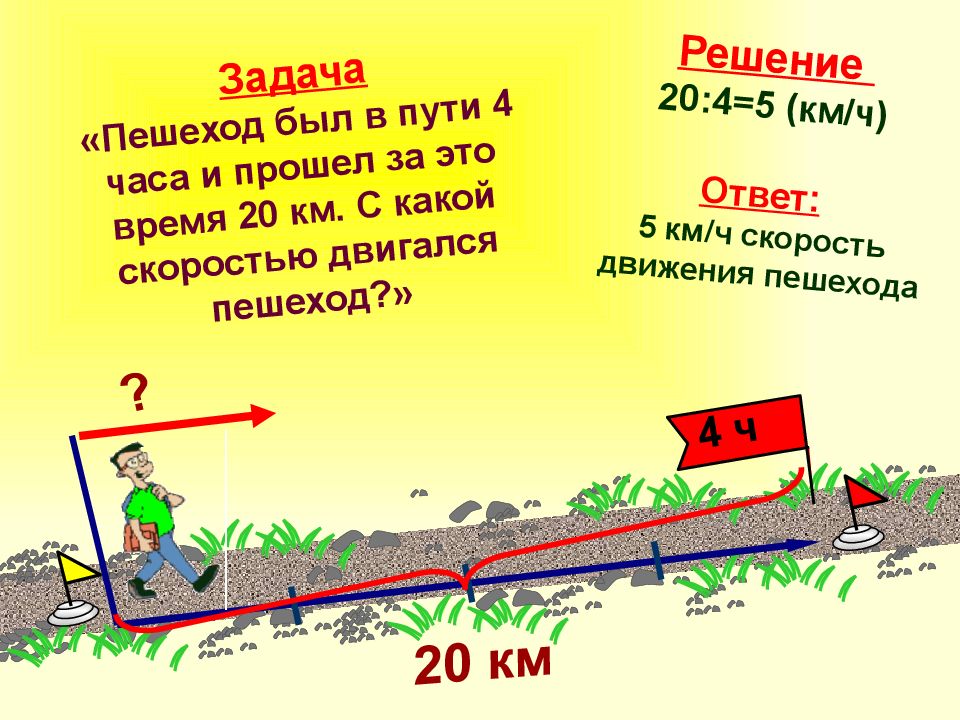
Слайд 9: Задача «Пешеход был в пути 4 часа и прошел за это время 20 км. С какой скоростью двигался пешеход?»
? 20 км 4 ч Решение 20:4=5 (км/ч) Ответ: 5 км/ч скорость движения пешехода
Слайд 10
V =S : t Чтобы узнать скорость движения, нужно расстояние разделить на время. Основные формулы
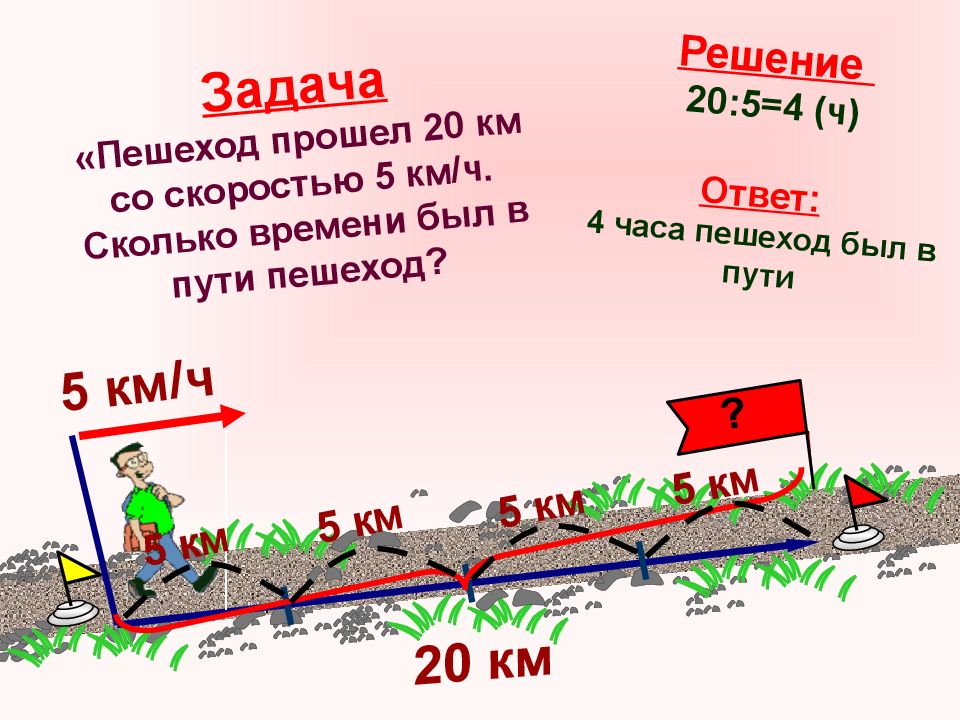
Слайд 11: Задача «Пешеход прошел 20 км со скоростью 5 км/ч. Сколько времени был в пути пешеход?
5 км/ч 20 км ? Решение 20:5=4 (ч) Ответ: 4 часа пешеход был в пути 5 км 5 км 5 км 5 км
Слайд 12
t =S : V Чтобы найти время движения, нужно расстояние разделить на скорость. Основные формулы
Слайд 13: Задача «Пешеход шел 4 часа, проходя каждый час 5 км. Какое расстояние прошел пешеход?
5 км/ч ? 4 ч Решение 5 x 4= 20 (км) Ответ: 20 км – расстояние, пройденное пешеходом 5 км 5 км 5 км 5 км
Слайд 14
S =V ∙ t Чтобы найти пройденное расстояние, нужно скорость движения умножить на время. Основные формулы
Слайд 15
Цель – познакомить учащихся с видами и способами решения задач на движение Задачи, решаемые на данном этапе: Решение задач на движение в противоположном направлении; Решение задач на встречное движение; Решение задач на движение в одном направлении. 2 этап
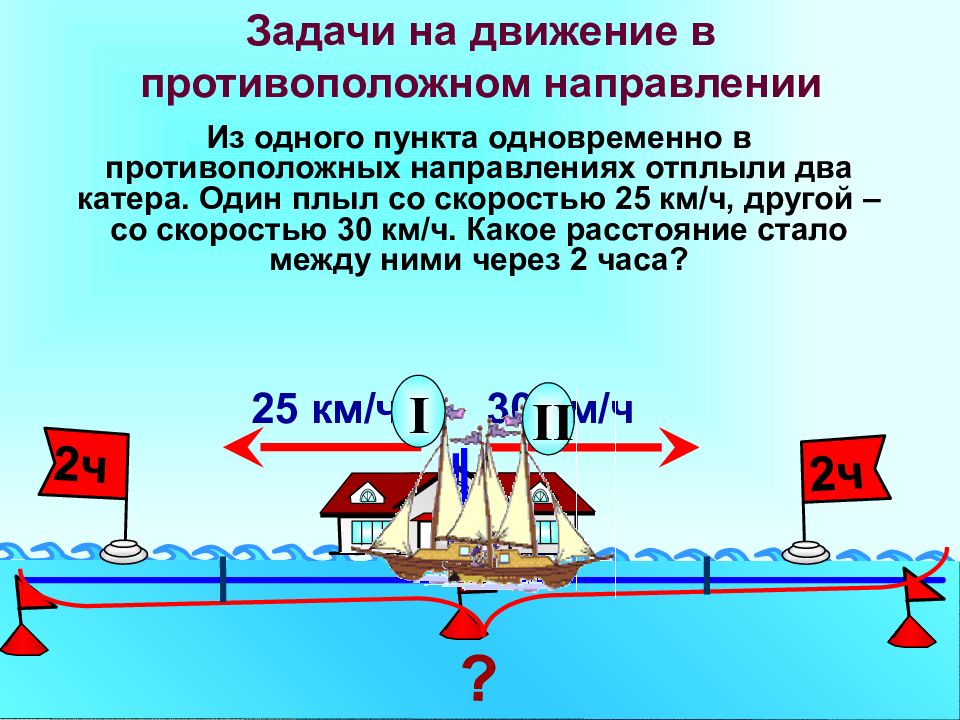
Из одного пункта одновременно в противоположных направлениях отплыли два катера. Один плыл со скоростью 25 км/ч, другой – со скоростью 30 км/ч. Какое расстояние стало между ними через 2 часа? 25 км/ч 30 км/ч ? I II 2ч 2ч
Слайд 17
2 способ Решение: 1) 25 + 30 = 55 (км/ч) – скорость удаления катеров 2) 55 x 2 = 110 (км) – расстояние между катерами через 2 часа Ответ: 110 км расстояние между катерами 1 способ Решение: 25 x 2 = 50 (км) – прошел первый катер за 2 часа 30 x 2 = 60 ( км) – прошел второй катер за 2 часа 50 + 60 = 110 (км) – расстояние между катерами через 2 часа Ответ: 110 км расстояние между катерами Сравни эти два способа решения задачи. Какое новое понятие вводится во втором способе решения? Что такое скорость удаления?
Слайд 18: Задачи на встречное движение
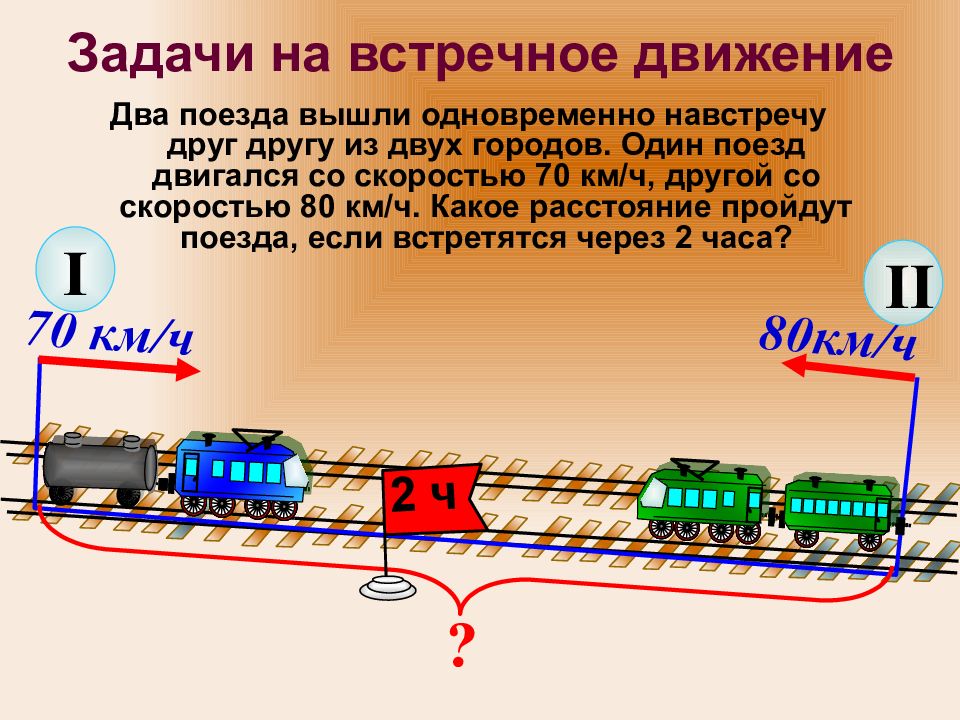
Два поезда вышли одновременно навстречу друг другу из двух городов. Один поезд двигался со скоростью 70 км/ч, другой со скоростью 80 км/ч. Какое расстояние пройдут поезда, если встретятся через 2 часа? ? 70 км/ч I 8 0км/ч II 2 ч
Слайд 19
2 способ Решение: 1) 70 + 80 = 150 (км/ч) – скорость сближения поездов 2) 150 x 2 = 300 (км) – расстояние, которое пройдут поезда Ответ: 300 км пройдут поезда 1 способ Решение: 70 x 2 = 140 (км) – прошел первый поезд за 2 часа 80 x 2 = 1 60 ( км) – прошел второй поезд за 2 часа 140 + 160 = 300 (км) – расстояние, которое пройдут поезда Ответ: 300 км пройдут поезда Сравни эти два способа решения задачи. Какое новое понятие вводится во втором способе решения? Что такое скорость сближения?
Слайд 20
При решении задач на встречное движение используют понятие « скорость сближения ». При решении задач на движение в противоположных направлениях применяют понятие « скорость удаления ». Скорость сближения и скорость удаления в этих задачах находится сложением скоростей движущихся объектов. V сбл. = V1 + V2 V уд. = V1 + V2 Делаем выводы
Слайд 21: Задачи на движение в одном направлении
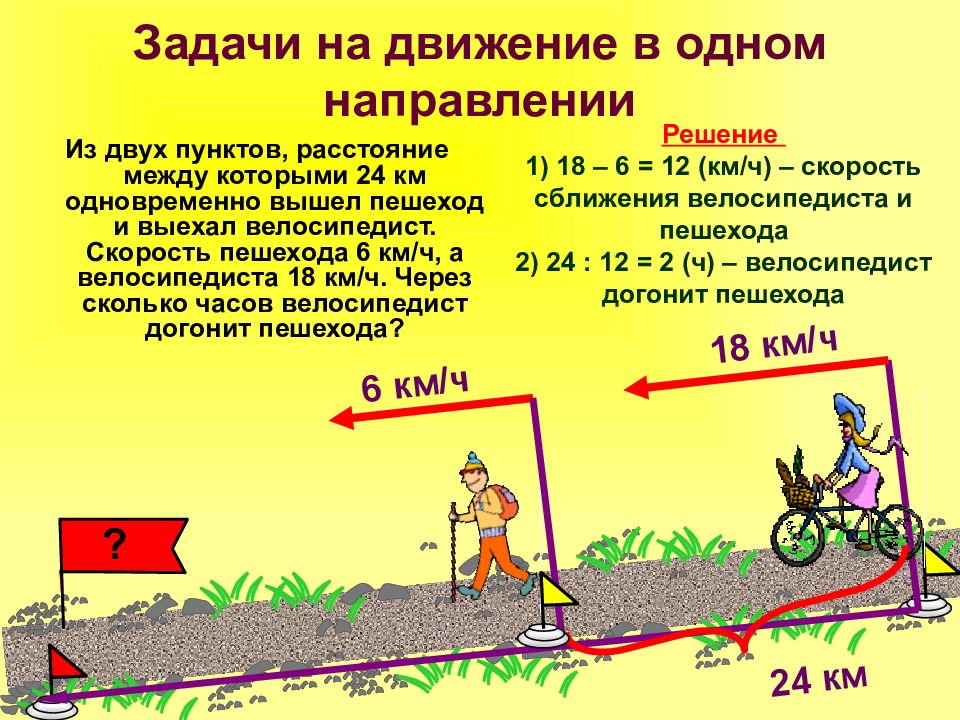
? Из двух пунктов, расстояние между которыми 24 км одновременно вышел пешеход и выехал велосипедист. Скорость пешехода 6 км/ч, а велосипедиста 18 км/ч. Через сколько часов велосипедист догонит пешехода? 18 км/ч 6 км/ч 24 км Решение 1 ) 1 8 – 6 = 12 ( км/ч) – скорость сближения велосипедиста и пешехода 2) 24 : 12 = 2 (ч) – велосипедист догонит пешехода
Слайд 22
Делаем выводы В задачах на движение в одном направлении при одновременном начале движения объектов используют понятия « скорость сближения » и « скорость удаления ». Скорость сближения и скорость удаления находятся вычитанием меньшей скорости из большей. V сбл. = V1 – V2 V уд. = V1 – V2
Слайд 23
Отвечаем на вопрос задачи Алгоритм решения задач на движение Устанавливаем объект движения, какая из величин по условию задачи является известной Устанавливаем, какая из величин по условию задачи является неизвестной Решаем задачу Выражаем неизвестную величину с помощью формул
Слайд 24
Цель – отработать у учащихся умение решать задачи на движение различными способами с помощью формул. 3 этап