Задачи на движение по прямой (навстречу и вдогонку)
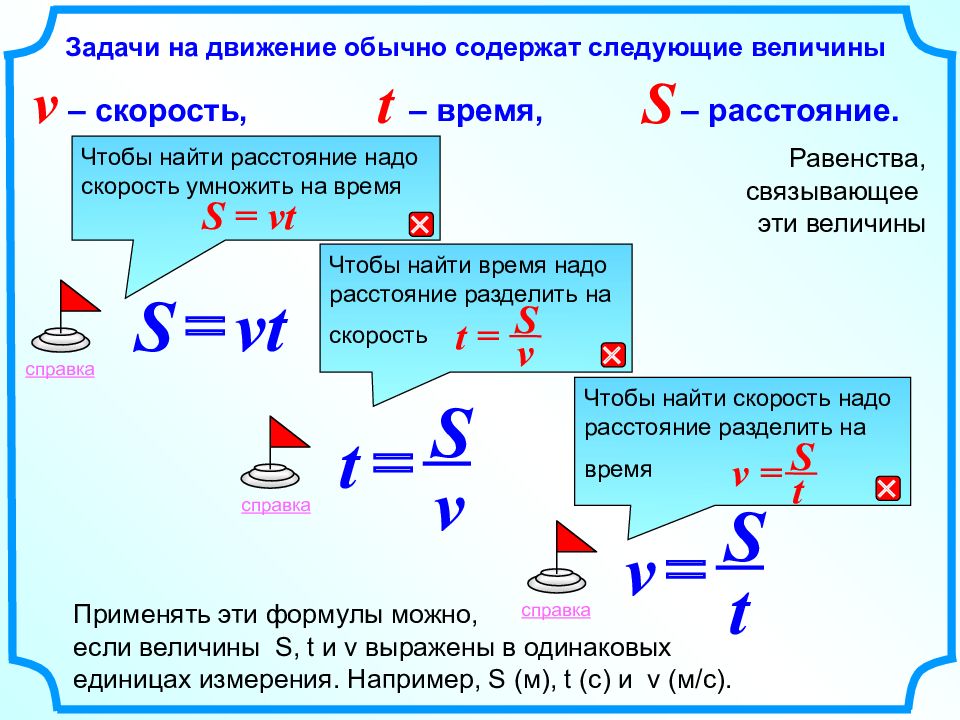
Задачи на движение обычно содержат следующие величины Равенства, связывающее эти величины vt S = v S t = t S v = Применять эти формулы можно, если величины S, t и v выражены в одинаковых единицах измерения. Например, S ( м), t (с) и v (м/с). справка t – время, S – расстояние. v – скорость, Чтобы найти скорость надо расстояние разделить на время v = S t справка Чтобы найти время надо расстояние разделить на скорость t = S v справка Чтобы найти расстояние надо скорость умножить на время S = vt
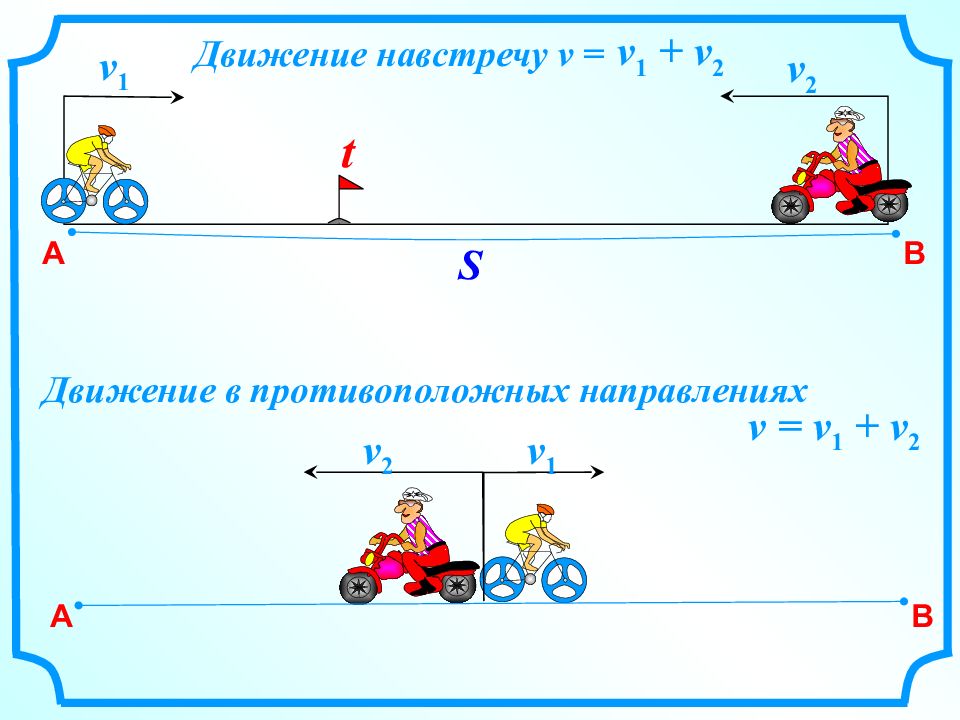
А B S t v 1 v 2 Движение навстречу v = v 1 + v 2 А B v 1 v 2 Движение в противоположных направлениях v = v 1 + v 2
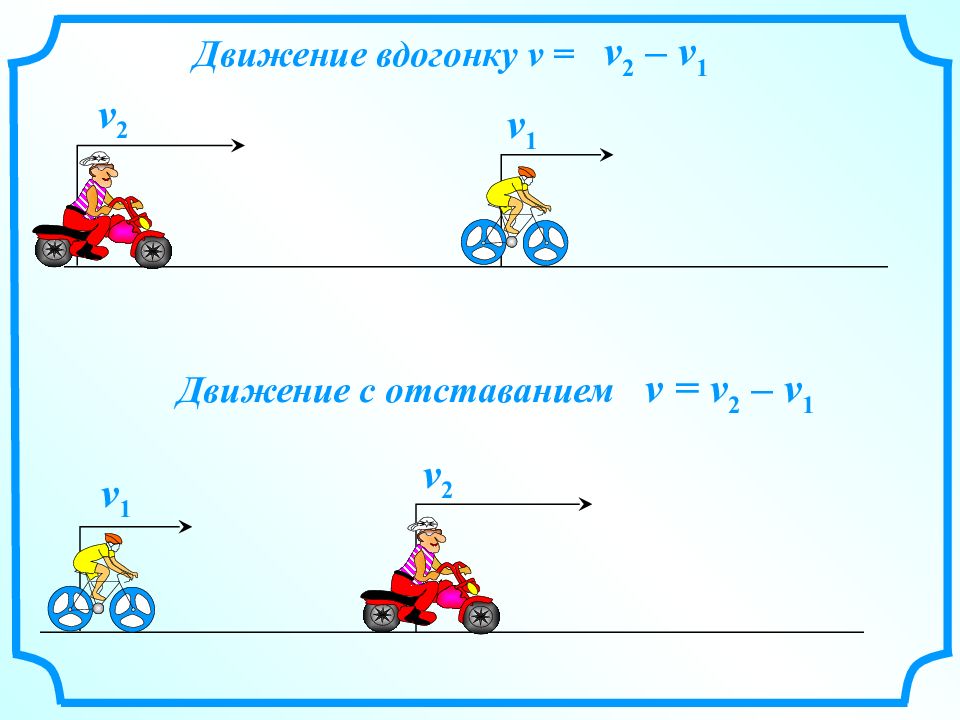
v 1 v 2 Движение вдогонку v = v 2 – v 1 v = v 2 – v 1 Движение с отставанием v 2 v 1
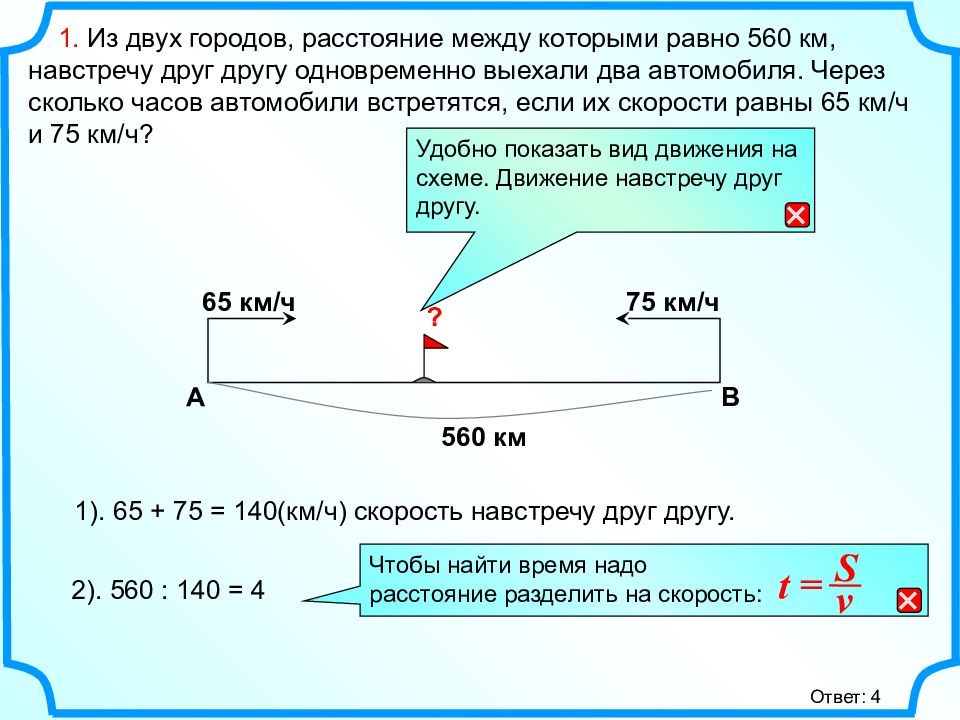
1. Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч? А B 560 км 1). 65 + 75 = 140(км/ч) скорость навстречу друг другу. 2). 560 : 140 = 4 ? 65 км/ч 75 км/ч Удобно показать вид движения на схеме. Движение навстречу друг другу. Ответ: 4 Чтобы найти время надо расстояние разделить на скорость : S v t =
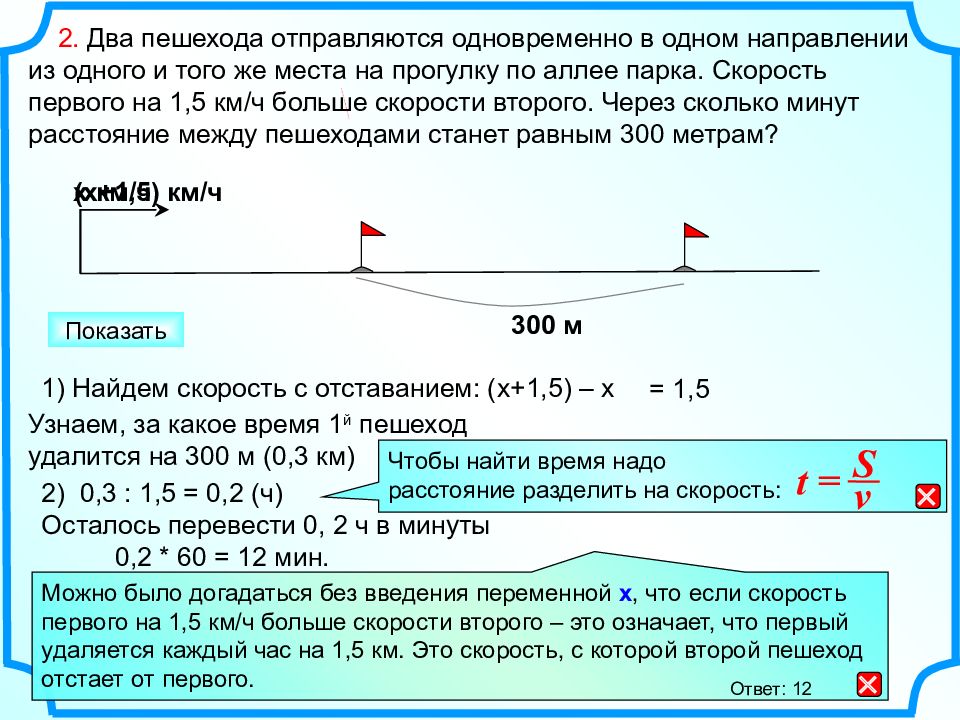
х км/ч 2. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам? 1) Найдем скорость с отставанием: (х+1,5) – х Узнаем, за какое время 1 й пешеход удалится на 300 м (0,3 км) (х+1,5) км/ч 300 м 2) 0,3 : 1,5 = 0,2 (ч) Осталось перевести 0, 2 ч в минуты 0,2 * 60 = 12 мин. Показать = 1,5 Можно было догадаться без введения переменной х, что если скорость первого на 1,5 км/ч больше скорости второго – это означает, что первый удаляется каждый час на 1,5 км. Это скорость, с которой второй пешеход отстает от первого. Ответ: 12 Чтобы найти время надо расстояние разделить на скорость : S v t =
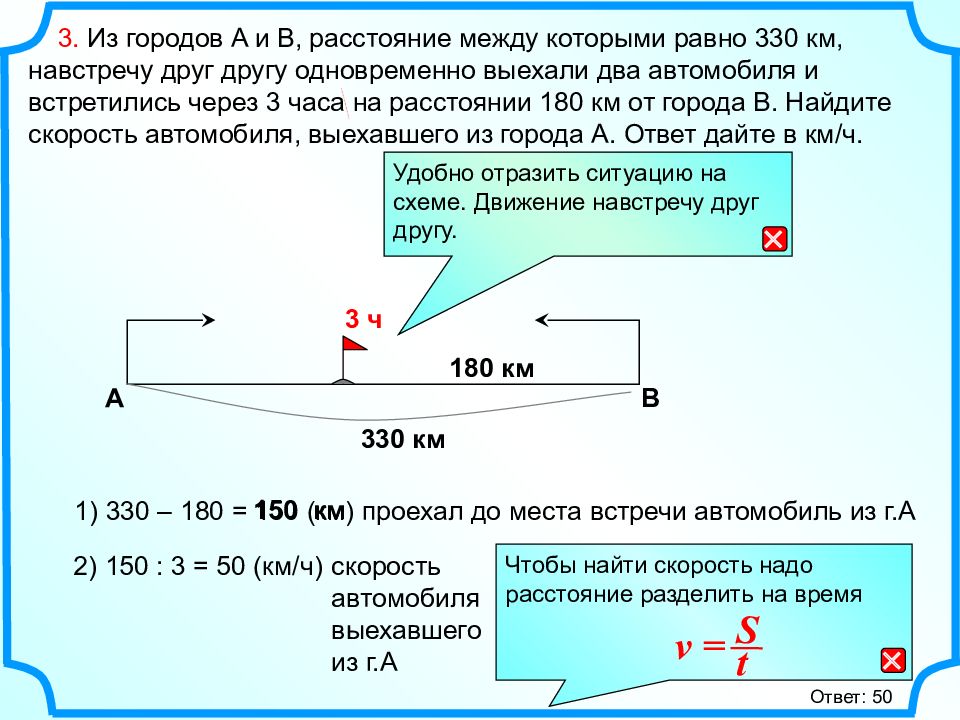
3. Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч. А B 180 км 330 км 1) 330 – 180 = 150 (км) проехал до места встречи автомобиль из г.А скорость автомобиля выехавшего из г.А Удобно отразить ситуацию на схеме. Движение навстречу друг другу. 3 ч 150 км Ответ: 50 Чтобы найти скорость надо расстояние разделить на время v = S t 2) 150 : 3 = 50 (км/ч)
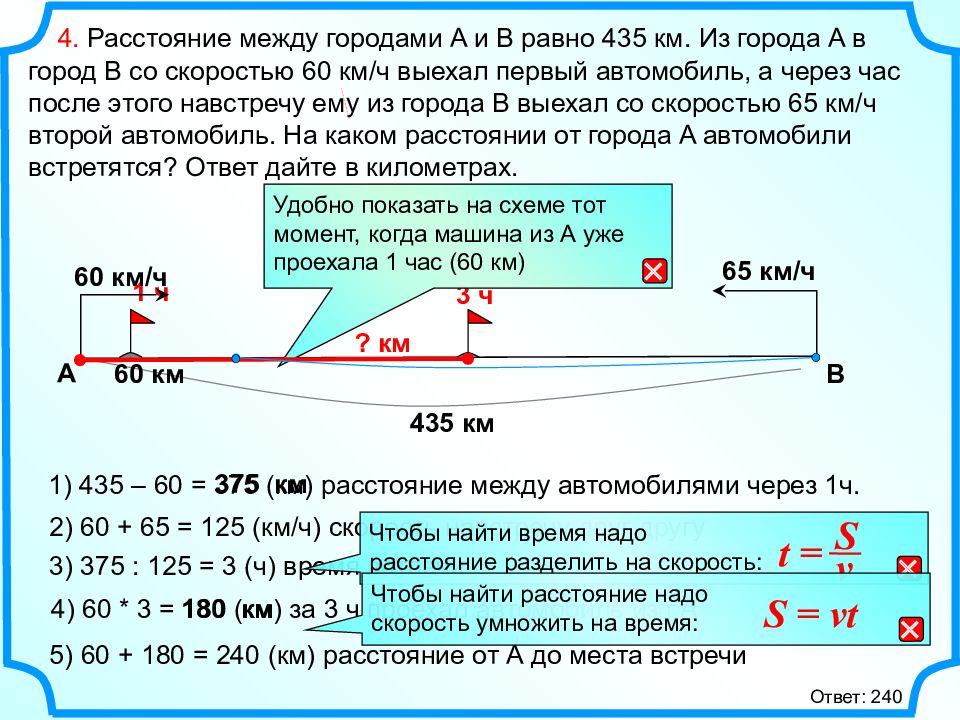
4. Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах. А 435 км 1) 435 – 60 = 375 (км) расстояние между автомобилями через 1ч. 2) 60 + 65 = 125 (км/ч) скорость навстречу друг другу 1 ч 375 км 60 км/ч 65 км/ч 60 км 3) 375 : 125 = 3 (ч) время встречи 3 ч 4) 60 * 3 = 180 (км) за 3 ч проехал автомобиль из г.А 5) 60 + 180 = 240 (км) расстояние от А до места встречи Удобно показать на схеме тот момент, когда машина из А уже проехала 1 час (60 км) Ответ: 240 180 км B ? км Чтобы найти время надо расстояние разделить на скорость : S v t = Чтобы найти расстояние надо скорость умножить на время : S = vt
5. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. 24 S 2(x+16) S х 1 автомобиль 2 автомобиль S, км S t, ч х v, км/ч x+16 S 2 S 2 S 2 24 S 2(x+16) S 2 24 S х + = : S S 2(x+16) S 2 24 + S х = Это условие поможет ввести х … I половина пути II половина пути Решите уравнение самостоятельно и найдите ответ на вопрос задачи. 32 км/ч Чтобы найти время надо расстояние разделить на скорость t = S v
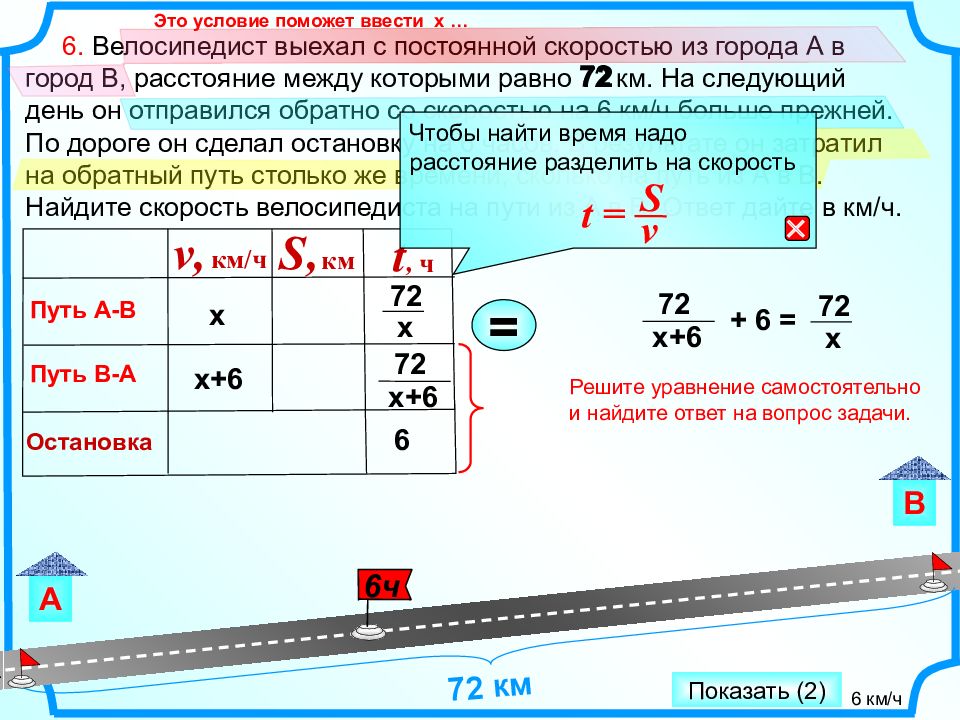
6. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 72 км. На следующий день он отправился обратно со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч. Путь В-А х Путь А-В v, км/ч t, ч S, км 72 х 72 х+6 72 = х+6 Решите уравнение самостоятельно и найдите ответ на вопрос задачи. Чтобы найти время надо расстояние разделить на скорость t = S v 72 Остановка 6 72 х+6 + 6 = 72 х А В 72 км 6ч Это условие поможет ввести х … 6 км/ч Показать (2)
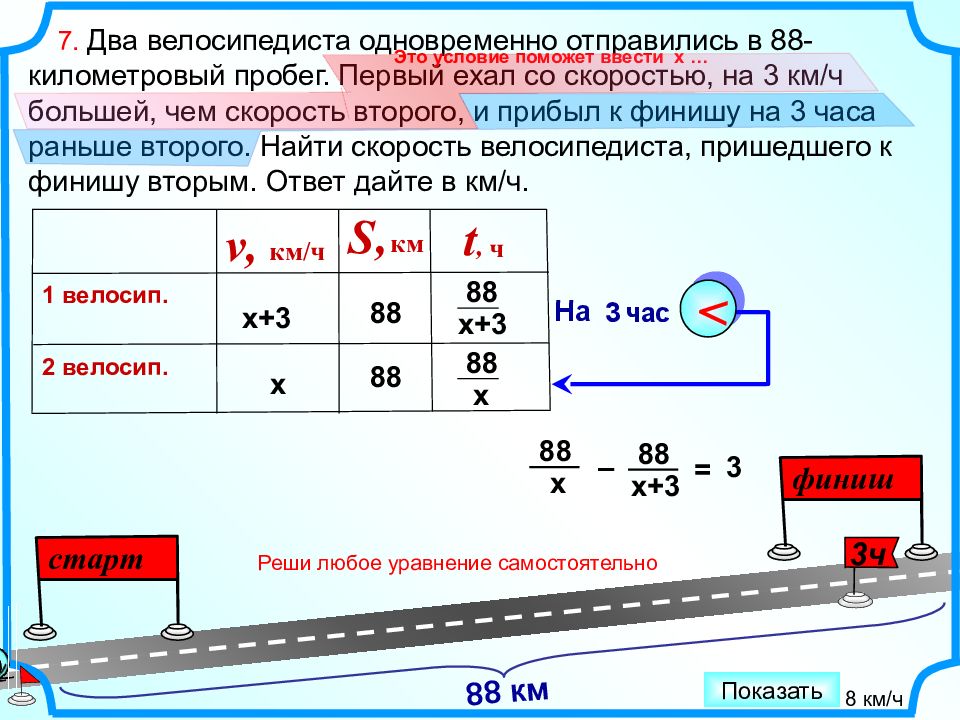
7. Два велосипедиста одновременно отправились в 88-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч. х S, км 88 х 88 х+3 1 велосип. 2 велосип. 88 88 t, ч На 3 час < Это условие поможет ввести х … Реши любое уравнение самостоятельно финиш старт 88 км 2 1 3ч х+3 v, км/ч 8 км/ч Показать = 88 х+ 3 88 х – 3
