Первый слайд презентации: Модели, описываемые системами двух автономных дифференциальных уравнений
Слайд 2: Основные понятия:
Фазовая плоскость. Фазовый портрет. Метод изоклин. Главные изоклины. Устойчивость стационарного состояния. Линейные системы. Типы особых точек: узел, седло, фокус, центр.
Слайд 3: Типы устойчивости стационарного состояния
Ляпунов Александр Михайлович (1857-1918) - выдающийся русский математик, создал теорию устойчивости состояний равновесия и движения механических систем с конечным числом параметров. Работал также в области дифференциальных уравнений, гидродинамики, теории вероятностей.
Слайд 4: Рассмотрим систему (1):
P( x,y ), Q( x,y )- непрерывные функции, определенные в некоторой области G евклидовой плоскости и имеющие в этой области непрерывные производные порядка не ниже первого.
Совокупность фазовых траекторий при различных начальных значениях переменных образует фазовый портрет системы.
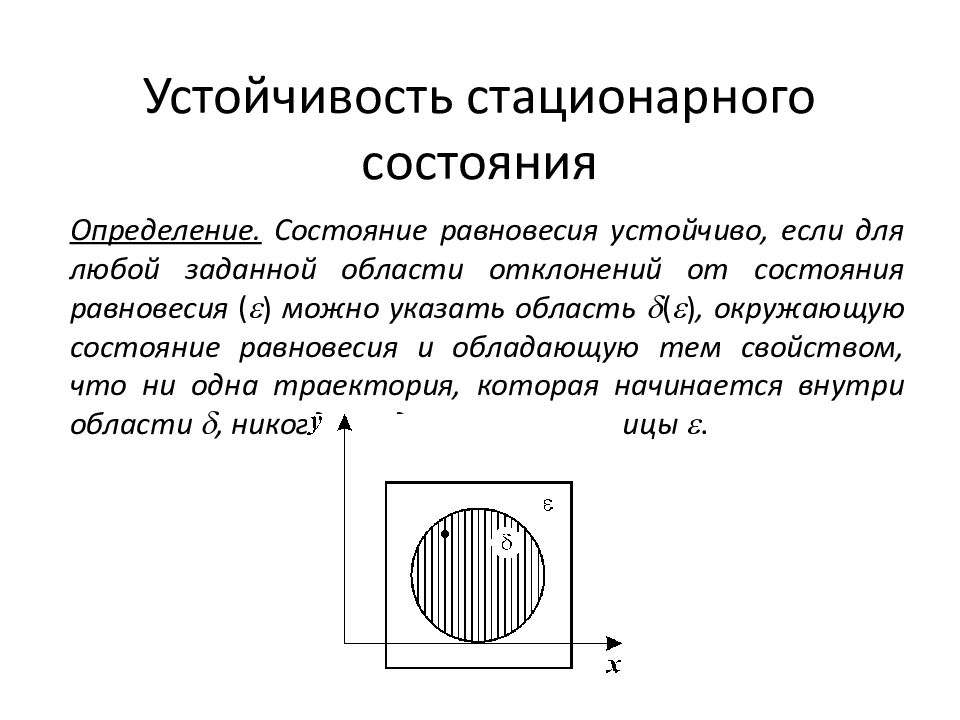
Слайд 8: Устойчивость стационарного состояния
Определение. Состояние равновесия устойчиво, если для любой заданной области отклонений от состояния равновесия ( ) можно указать область ( ), окружающую состояние равновесия и обладающую тем свойством, что ни одна траектория, которая начинается внутри области , никогда не достигнет границы .
Слайд 9: Линейные системы
Типы поведения траекторий в окрестности стационарного состояния (2) (3) (4)
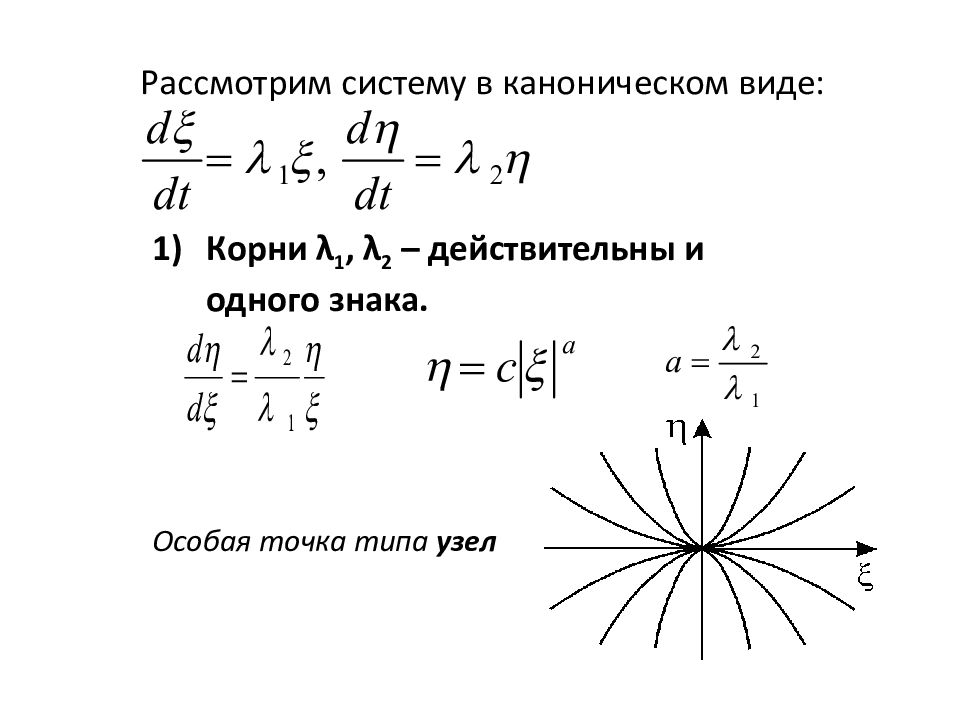
Слайд 10: Рассмотрим систему в каноническом виде:
Корни λ 1, λ 2 – действительны и одного знака. Особая точка типа узел
Слайд 11
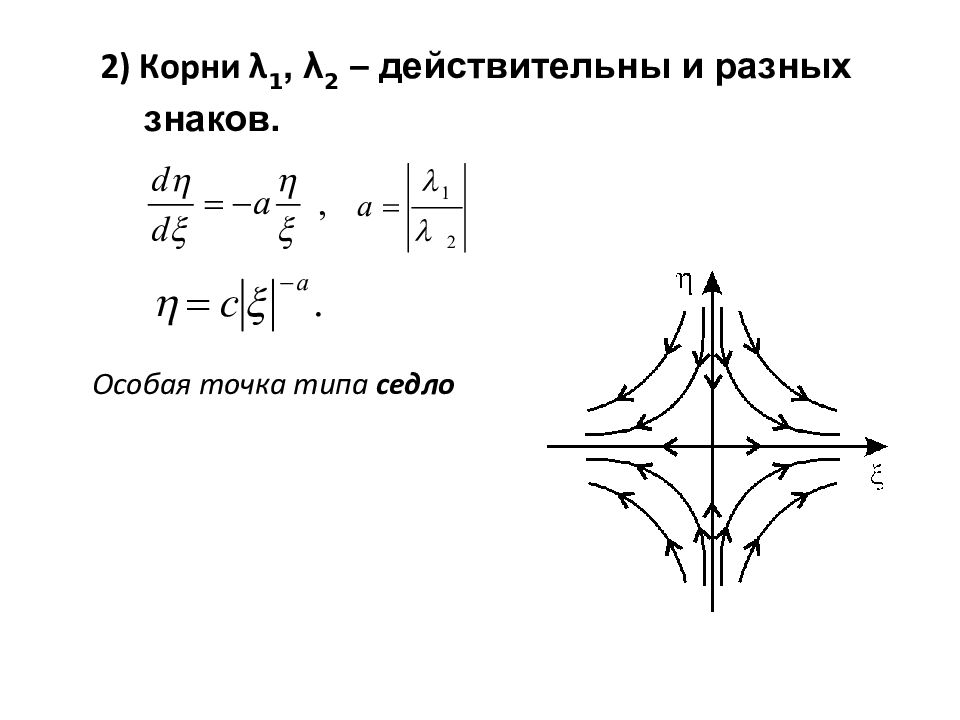
2) Корни λ 1, λ 2 – действительны и разных знаков. Особая точка типа седло
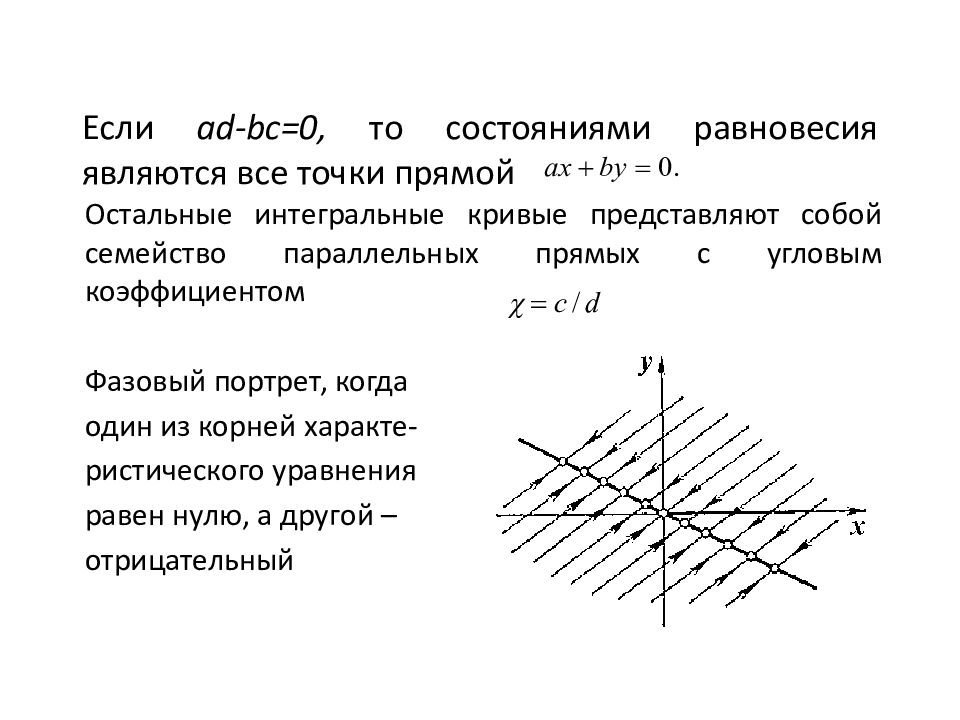
Слайд 12: Если ad-bc=0, то состояниями равновесия являются все точки прямой
Остальные интегральные кривые представляют собой семейство параллельных прямых с угловым коэффициентом Фазовый портрет, когда один из корней характе- ристического уравнения равен нулю, а другой – отрицательный
Слайд 13
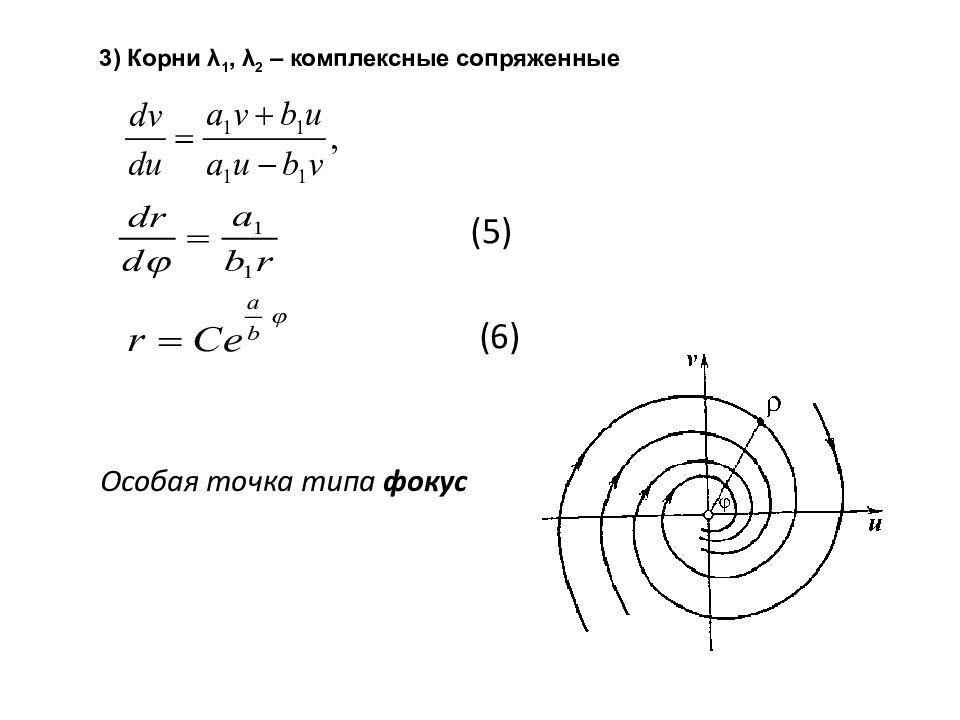
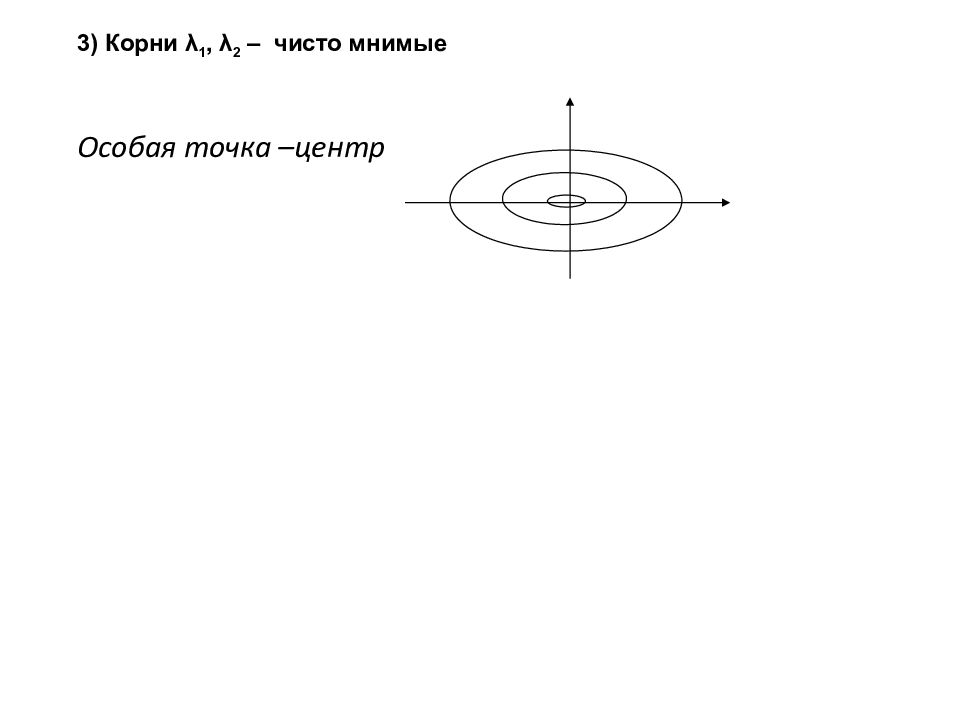
(5) (6) Особая точка типа фокус 3) Корни λ 1, λ 2 – комплексные сопряженные
Слайд 15
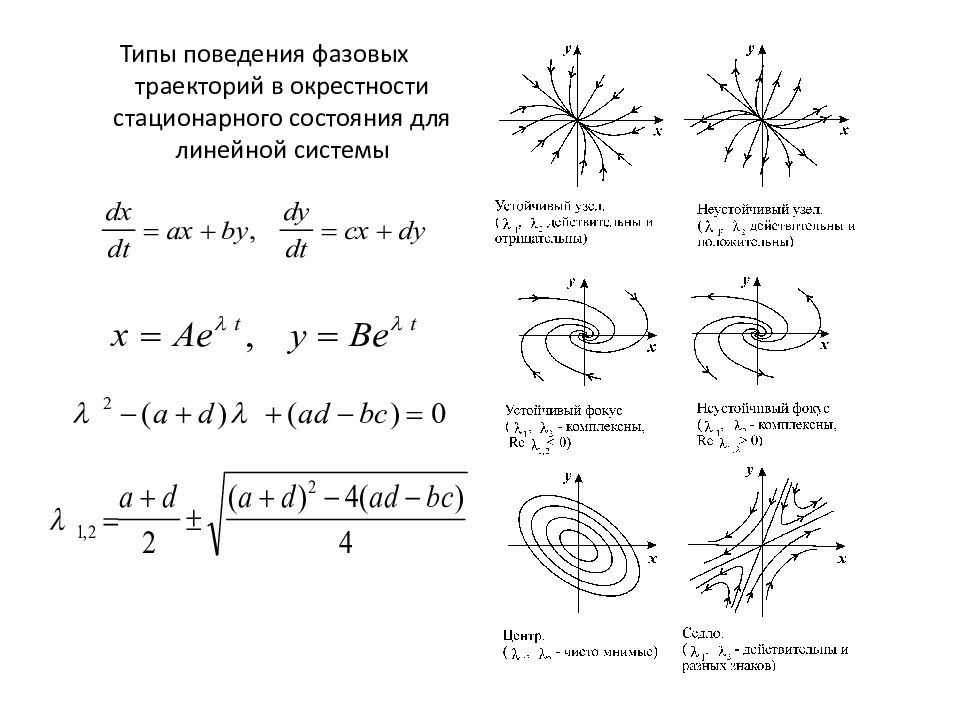
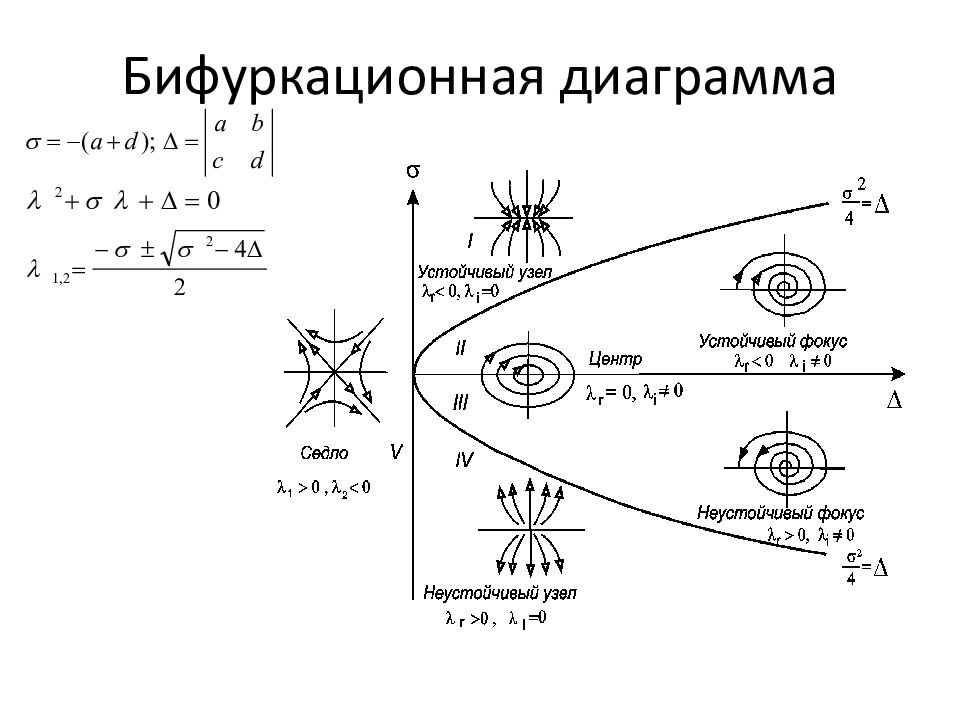
Типы поведения фазовых траекторий в окрестности стационарного состояния для линейной системы
Последний слайд презентации: Модели, описываемые системами двух автономных дифференциальных уравнений
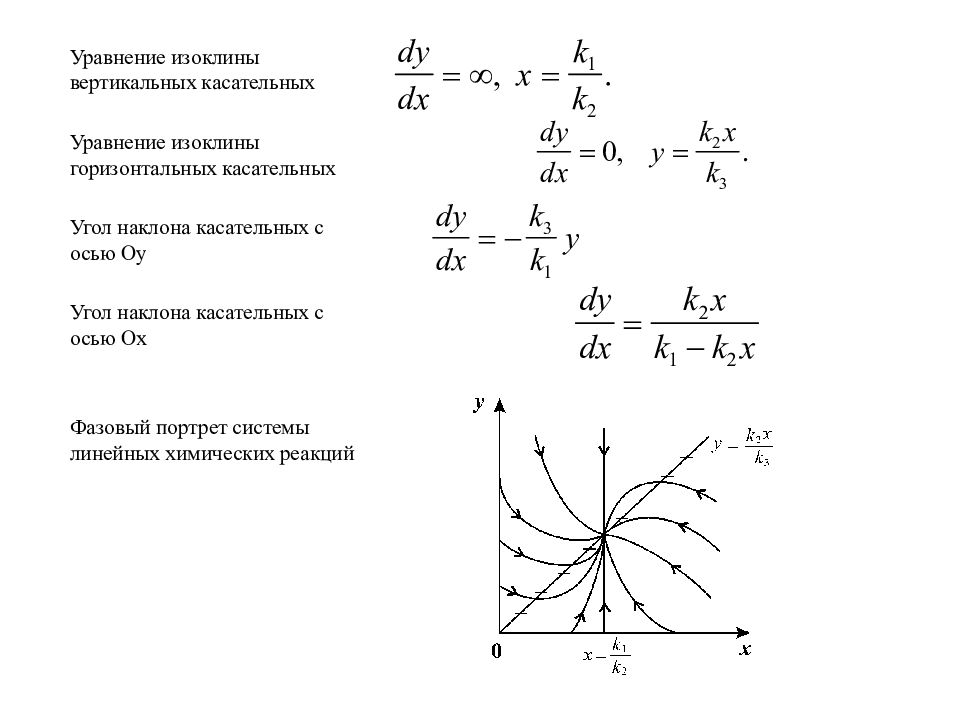
Уравнение изоклины вертикальных касательных Уравнение изоклины горизонтальных касательных Угол наклона касательных с осью Оу Угол наклона касательных с осью Ох Фазовый портрет системы линейных химических реакций