Первый слайд презентации: Основы термодинамики необратимых процессов
Слайд 2: ЛИНЕЙНАЯ НЕРАВНОВЕСНАЯ ТЕРМОДИНАМИКА
Связь между потоком и термодинамической силой вблизи термодинамического равновесия Взаимодействие термодинамических процессов Линейные феноменологические уравнения взаимности Онзагера Соотношение взаимности Онзагера Скорость диссипации энергии
Открытая система Значения движущих сил малы Сами процессы протекают медленно J = LX X – термодинамические силы (градиенты интенсивных параметров) J – сопряженные с ними потоки L – коэффициент, не зависящий от величины Х
J = LX I = Δ U/R dc/dt = J c = -D c dQ/dt = J Q = - λ T Закон Фика Закон Ома Закон Фурье
Слайд 5: Связь между потоком и термодинамической силой вблизи термодинамического равновесия
J = LX |A ij |/RT << 1 |A ij | < RT Величина L определяется равновесным состоянием
Слайд 6: Принцип взаимодействия термодинамических процессов
1931 Если в системе одновременно протекает несколько термодинамических процессов, то они способны взаимодействовать между собой. Скорость каждого будет зависеть от движущих сил всех процессов Л. Онзагер
Слайд 7: Принцип взаимодействия термодинамических процессов
1931 Л. Онзагер Линейные феноменологические уравнения взаимности Онзагера
Слайд 8: Линейные феноменологические уравнения взаимности Онзагера
Взаимодействие двух процессов Линейные феноменологические уравнения взаимности Онзагера L 12, L 21 – коэффициенты взаимности Онзагера
Слайд 9: Соотношение взаимности Онзагера
соотношение взаимности Онзагера L ij = L ji Принцип Кюри: значения L ij отличны от нуля, когда взаимодействующие силы Х j имеют одинаковую тензорную размерность Если поток необратимого процесса i испытывает влияние термодинамической силы Х j необратимого процесса j через коэффициенты L ij, то и поток процесса j также испытывает влияние термодинамической силы Х i через тот же самый коэффициент L ij
Слайд 10: Скорость диссипации энергии
Скорость производства энтропии Скорость диссипации энергии
Слайд 12: Взаимодействующие процессы в однородных системах
Транспорт вещества через мембрану при наличии осмоса J 1 – поток растворителя через мембрану J 2 – поток растворенного вещества через мембрану Δ р – разность гидростатических давлений в разделенных фазах Δπ – разность осмотического давления вещества
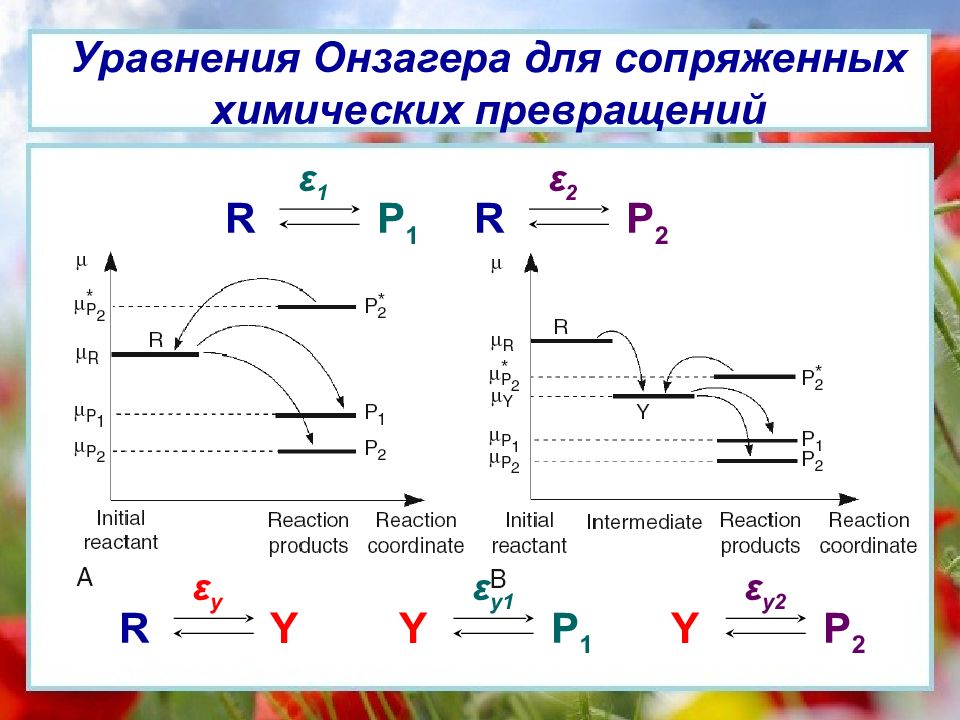
Слайд 13: Уравнения Онзагера для сопряженных химических превращений
ε 1 R P 1 ε 2 R P 2 ε y1 Y P 1 ε y R Y ε y2 Y P 2
Слайд 14: Уравнения Онзагера для сопряженных химических превращений
ε y1 Y P 1 ε y R Y ε y2 Y P 2
Слайд 15: Уравнения Онзагера для сопряженных химических превращений
ε y1 Y P 1 ε y R Y ε y2 Y P 2
Слайд 16: Уравнения Онзагера для сопряженных химических превращений
ε y1 Y P 1 ε y R Y ε y2 Y P 2 При протекании в системе параллельных брутто-реакций, их скорости являются взаимозависимыми Обобщение правила Хориути-Борескова для произвольной системы параллельных процессов, протекающих с общим интермедиатом
Слайд 17: Сопряженные процессы в пространственно –неоднородных системах
Эффект Зеебека (1821) Возникновение термоЭДСв замкнутой электрической цепи при использовании в цепи разных металлов и поддержании спаев этих металлов при разной температуре Измерение температуры с помощью термопары. Томас Йоган Зеебек
Слайд 18: Сопряженные процессы в пространственно –неоднородных системах
Эффект Пельтье (1834) Выделение или поглощение теплоты на контакте двух разных проводников. Холодильники с охлаждающим элементом в виде контакта двух подобранных полупроводников. Жан Шарль Пельтье
Слайд 19: Сопряженные процессы в пространственно –неоднородных системах
Эффект Томсона (1856) Выделение или поглощение в однородном неравномерно нагретом проводнике дополнительной теплоты за счет совместного действия электропроводности и теплопроводности. Уильям Томсон, лорд Кельвин
Слайд 20: Сопряженные процессы в пространственно –неоднородных системах
Термомеханический эффект Возникновение разности давлений в резервуарах с жидкостью или газом, соединенных капилляром при поддержании в резервуарах разных температур. Если резервуары разделены пористой перегородкой, эффект называется термоосмосом.
Слайд 21: Сопряженные процессы в пространственно –неоднородных системах
Механокалорический эффект Возникновение разности температур в резервуарах с жидкостью или газом, соединенных капилляром в результате создания разности давлений в сосудах.
Слайд 22: Термодинамические критерии устойчивости стационарных состояний
Стационарное состояние характеризуется неизменностью во времени внутренних параметров системы и отсутствием потоков этих параметров. Значение внутренних параметров определяется протеканием внутренних процессов, возбуждаемых внутренними силами. Возможно установить взаимосвязь между скоростью производства энтропии за счет самопроизвольных необратимых процессов внутри системы и установлением в ней стационарного состояния.
Слайд 23: Термодинамические критерии устойчивости стационарных состояний
Открытая система с одновременно протекающими m процессами, находящаяся вблизи равновесия Справедливы линейные соотношения взаимности Онзагера Диссипативная функция Рэлея - Онзагера
Слайд 24: Термодинамические критерии устойчивости стационарных состояний
Диссипативная функция Рэлея - Онзагера Условие достижения стационарного состояния (по внутренней переменной і ):
Слайд 25: Термодинамические критерии устойчивости стационарных состояний
Диссипативная функция Рэлея - Онзагера Условие достижения стационарного состояния (по внутренней переменной і ): Условие минимума функционала Рэлея-Онзагера Система с любым числом процессов, связанных линейными соотношениями взаимности Онзагера
Слайд 26: Теорема И. Пригожина (1947)
При неизменных внешних условиях в стационарном и близком к термодинамическому равновесию состоянии открытой системы значение скорости производства энтропии за счет внутренних необратимых процессов является положительным, постоянным и минимальным Принцип минимума производства энтропии
Слайд 27: Теорема И. Пригожина (1947)
Характер изменения скорости производства энтропии позволяет обнаружить переход системы в стационарное состояние Принцип минимума производства энтропии Принцип минимума диссипации энергии Количественный критерий для определения общего направления самопроизвольных изменений в открытой системе (критерий эволюции системы)
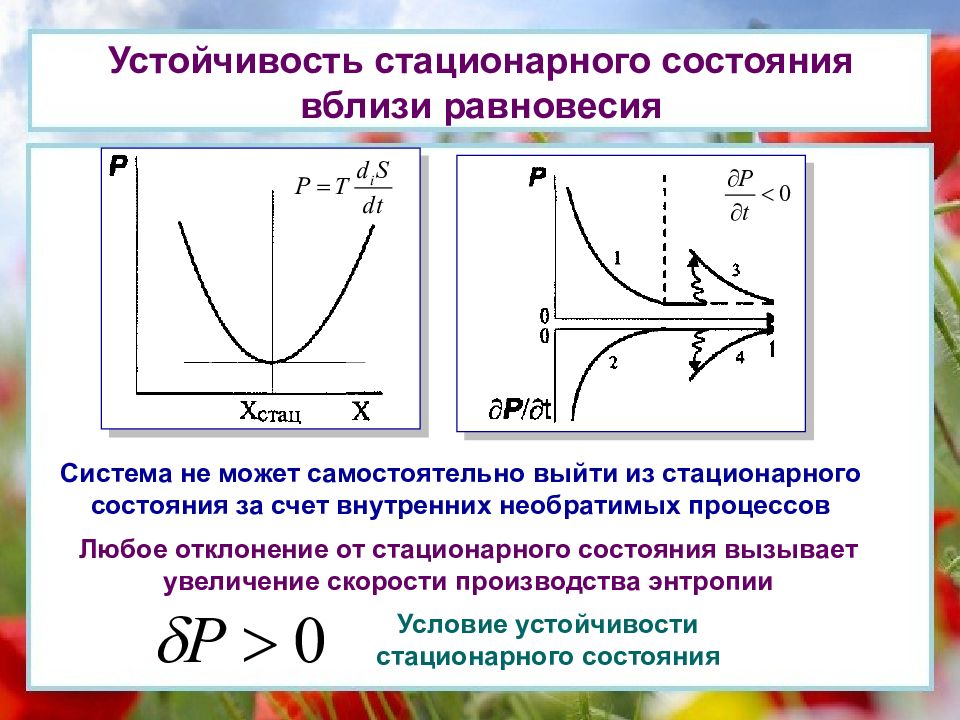
Слайд 28: Устойчивость стационарного состояния вблизи равновесия
Система не может самостоятельно выйти из стационарного состояния за счет внутренних необратимых процессов Любое отклонение от стационарного состояния вызывает увеличение скорости производства энтропии Условие устойчивости стационарного состояния
Слайд 29: Устойчивость стационарного состояния вблизи равновесия
В устойчивой системе поток, вызванный возмущением, будет стремиться уменьшить возмущение и вернуть систему в первоначальное состояние Условие устойчивости стационарного состояния Вблизи термодинамического равновесия невозможны автоколебательные процессы
Слайд 30: Подходы к анализу устойчивости состояний термодинамических систем
Классическая теория Гиббса (устойчивость равновесных систем) Теория устойчивости стационарных состояний (устойчивость неравновесных систем) Теория А.М. Ляпунова (общие критерии устойчивости)
Слайд 31: Общие критерии устойчивости стационарных состояний
Анализ термодинамических сил, возникающих в системе при отклонении от стационарного состояния. Если система находится в устойчивом стационарном состоянии, то при отклонении от этого состояния в ней должны возникнуть силы, возвращающие систему в первоначальное положение.
Слайд 32: Общие критерии устойчивости стационарных состояний
Система в возмущенном состоянии начинает диссипировать энергию с большей скоростью, поэтому самопроизвольно возвращается из возмущенного состояния к первоначальному стационарному При отрицательном избыточном производстве энтропии возникшая в стационарном состоянии флуктуация не приведет к самопроизвольному возвращению системы в стационарное состояние. Первоначальное стационарное состояние не было устойчивым