МОДУЛЬ № 1 ПРОПУСКНА ЗДАТНІСТЬ ТА ОЦІНКА СТІЙКОСТІ СТЕГАНОГРАФІЧНИХ СИСТЕМ Сіденко Володимир Павлович, Старший викладач кафедри “Безпека інформаційних та комунікаційних систем” 1
Лекція № 4 ІНФОРМАЦІЙНЕ ПРИХОВУВАННЯ ПРИ АКТИВНОЇ ПРОТИДІЇ ПОРУШНИКА 2
Питання лекції № 4 1. Поняття пропускної здатності каналів передавання даних, які приховуються 2. Інформаційне приховання при активній протидії порушника Література: Л2, с. 33 – 50. 3
1. ПОНЯТТЯ ПРОПУСКНОЇ ЗДАТНОСТІ КАНАЛІВ ПЕРЕДАВАННЯ ДАНИХ, ЯКІ ПРИХОВУЮТЬСЯ 4
Для розроблювальних або досліджу- ваних стеганографічних систем важливо визначити, наскільки великий може бути пропускна здатність створюваних при цьому каналів передачі приховуваних да- них ( КППД ), і як вона буде залежати від ін- ших характеристик стеганосистем і умов їх використання. Під пропускною здатністю каналів передачі приховуваних даних або просто схованою пропускною здатністю ( СПЗ ) розуміють максимальну кількість інфор- мації, яка може бути вбудована в один 5
елемент (наприклад, піксель або часовий відлік) контейнера. Обов'язковою умовою при цьому є безпомилковість передачі приховуваних даних одержувачеві, а також їх захищеність від таких атак порушника як спроба виявлення факту наявності каналу схованому зв'язку, одержання змісту схо- ваних повідомлень, навмисне введення сфальсифікованих даних або ж руйнуван- ня вбудованої в контейнер інформації. 6
7 Канал схованого зв'язку ( КСЗ ) утво- рюється усередині каналу відкритого зв'яз- ку ( КВЗ ), для якого Шенон (Shannon) у своїх роботах з теорії інформації визначив про- пускну здатність. Пропускна здатність КВЗ визначається як кількість інформації, яку потенційно можна передати без помилок за одне вико- ристання каналу. При цьому не висуваєть- ся жодного вимоги до захищеності від атак організованого порушника.
Тому буде зовсім логічно припустити, що схована пропускна здатність КСЗ, у яко- му за одне використання каналу передаєть- ся один елемент контейнера із вкладеної до нього схованою інформацією, у жодно- му разі не може бути більше пропускної здатності КВЗ. На сьогоднішній день намітилися різні, іноді діаметрально протилежні підходи до визначення кількості інформації, яка під- лягає захисту від різноманітних атак по- рушника за допомогою стеганографічних методів. 8
Ці розбіжності обумовлені відміннос- тями з метою захисту інформації, видах по-рушників, їх можливостях і реалізованих атаках на стеганосистеми, видах викорис- товуваних контейнерів і приховуваних по-відомлень і багатьма іншими факторами. Пропонується виконати оцінку величи- ни ПЗ КППД методами теорії інформації для різних стеганосистем. Теоретико-інформаційні методи дозво- ляють одержати строгі оцінки кількості приховуваної інформації, які зовсім право- мірно можуть бути використані як теоретич- 9
досяжні граничні швидкості передачі схо-ваної інформації для стеганосистем, не враховуючи принципи, закладені в основу їх побудови. Пропонується розглянути два основні підходи до оцінки пропускної здатності КППД. Перший з них орієнтований на стегано- графічні системи, у яких повідомлення, що підлягають захисту, повинні бути безпо- милково передані в умовах активної про- тидії порушника. 10
Цей підхід описує сценарій прихову- вання так званих безнадлишкових повідом- лень у даних контейнера, і, що найголов- ніше, дозволяє враховувати той факт, що крім викривлень структури контейнера при вбудовуванні в нього приховуваних даних, можливі його навмисні викривлення з боку порушника. Крім того, існує ще й імовір- ність викривлень випадкового характеру, викликаних ненавмисними перешкодами в каналі зв'язку. 11
Порушник, крім пасивних дій аналізу, може використовувати й активні дії (актив- ний порушник). Метою активного порушника є руйну- вання схованої інформації. Така постанов- ка завдання інформаційного приховання є характерної, наприклад, для систем ЦВЗ. Завдання інформаційного приховання формулюється як завдання безпомилкової передачі приховуваної інформації при впливі випадкових і навмисних перешкод, а також визначену максимальну швидкість безпомилкової передачі при різних страте- 12
гіях дій відправника й атакуючого. Запропонований підхід визначає тео- ретично досяжну швидкість достовірної передачі приховуваних повідомлень, хоча в явному виді й не оцінює захищеність останніх від виявлення факту їх існування. Однак для ряду стеганосистем не пот- рібно приховувати факт використання сте-ганографічного захисту: власник авторсь- ких або майнових прав на медіаконтейнер, який захищений ЦВЗ, як правило, відкрито повідомляє про застосування даної систе- ми захисту. 13
У розглянутому підході досліджуються умови, при яких приховувана інформація гарантовано передається в умовах довіль- них спроб порушника щодо її руйнування. Знання параметрів стеганосистеми й можливих стратегій дій передавальної сто- рони не повинне дозволити порушникові оптимізувати руйнівний вплив і оцінити його ефективність. Особливістю таких стеганосистем є: По-перше, те, що руйнівний вплив від- бувається тільки в момент передачі схова- них даних і повинне здійснюватися в режи- 14
мі реального часу. По-друге, існує апріорна непоінформо- ваність законного одержувача відносно приховано переданої йому інформації. По-третє, порушник у переважній біль- шості випадків не здатний вірогідно оці- нити ефективність своїх дій. Інша ситуація виникає при спробі ак- тивного порушника зруйнувати ЦВЗ із ме- тою привласнити собі контейнер (права на нього). 15
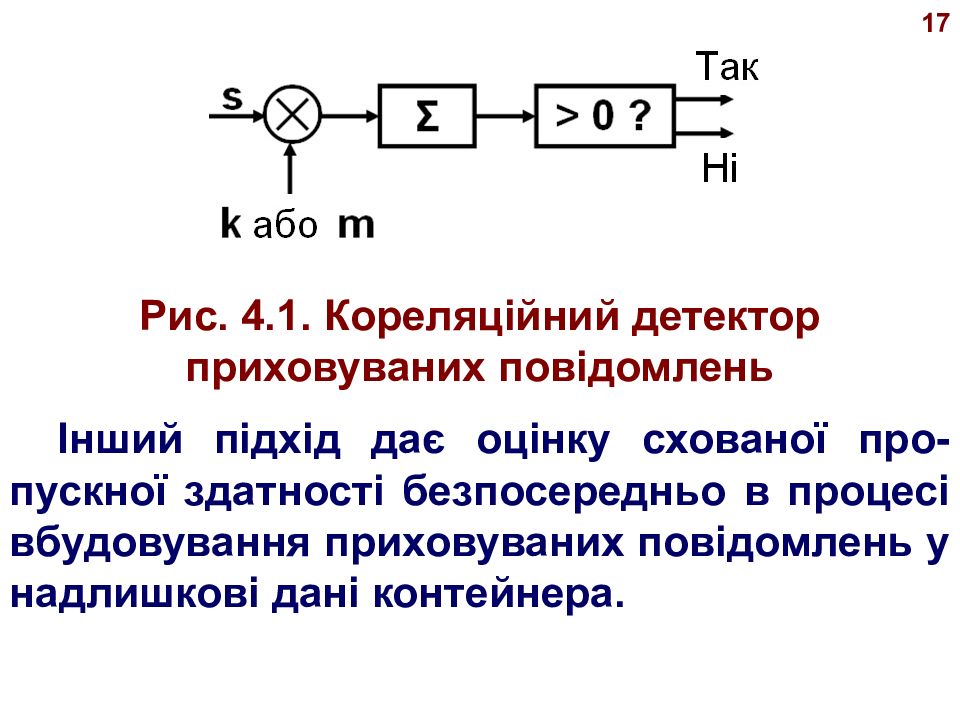
Порушник може як завгодно довго здійснювати руйнівний вплив, вибираючи таку оптимальну стратегію, при якій, зруй- нувавши ЦВЗ, він збереже необхідне йому якість контейнера. При цьому він заздалегідь знає про іс-нування схованої інформації, і, використо- вуючи загальновідомий детектор (див. рис. 4.1.), здатний оцінити ефективність своїх атак на ЦВЗ. 16
17 Рис. 4.1. Кореляційний детектор приховуваних повідомлень Інший підхід дає оцінку схованої про- пускної здатності безпосередньо в процесі вбудовування приховуваних повідомлень у надлишкові дані контейнера.
Такий підхід ураховує, що контейнери формуються реальними надлишковими джерелами з істотною пам'яттю, такими як джерела зображень або аудиосигналів. У цьому випадку оцінка ПЗ залежить від характеристик замаскованості сховано- го каналу. Такий підхід орієнтований на стега- носистеми, у яких реалізується схована передача апріорно невідомої одержувачеві інформації, причому пасивний порушник намагається в процесі спостереження за ка- 18
налом відкритого зв'язку виявити факт наявності КСЗ і, у випадку встановлення останнього, прагне розкрити зміст схова- ного повідомлення в перехопленому кон- тейнері. Відомо велика кількість робіт із син- тезу стеганосистем, автори яких пропо- нують різноманітні способи вбудовування даних у надлишкові по своїй природі кон- тейнери. 19
При цьому кількість інформації, вбудо- ваність якої залишається непоміченої, оці- нюється за допомогою додатково введе- них критеріїв рівня прихованості. Існуючі на сьогоднішній день оцінки схованої пропускної здатністю таких сте- ганоканалов, однак, не враховують можли- ві випадкові й навмисні викривлення кон- тейнерів при їхній передачі по каналу зв'язку. 20
21 2. ІНФОРМАЦІЙНЕ ПРИХОВАННЯ ПРИ АКТИВНІЙ ПРОТИДІЇ ПОРУШНИКА У рамках першого підходу до оцінки схованої пропускної здатності, розглянемо загальне формулювання завдання інфор- маційного приховання у випадку активної протидії з боку порушника.
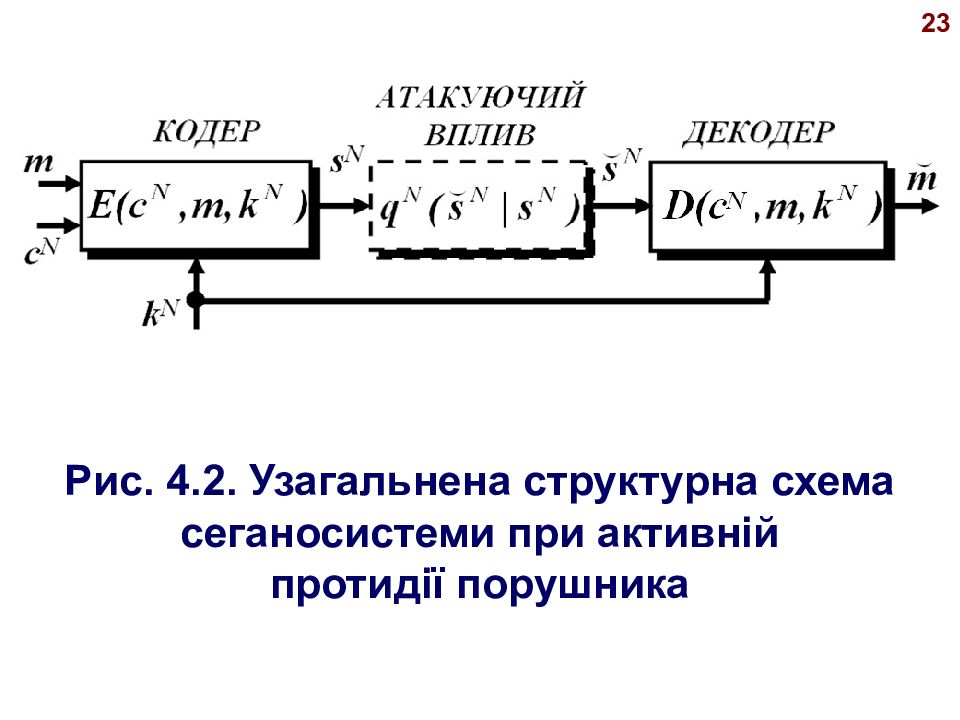
22 2.1. ФОРМУЛЮВАННЯ ЗАВДАННЯ ІНФОРМАЦІЙНОГО ПРИХОВАННЯ ПРИ АКТИВНІЙ ПРОТИДІЇ ПОРУШНИКА Розглянемо узагальнену структурну схему стеганографічної системи передачі схованих повідомлень, представленої на рис. 4.2.
23 Рис. 4. 2. Узагальнена структурна схема сеганосистеми при активній протидії порушника
24 У цій схемі приховувані повідомлення m рівномірно розподілені в множині пові - домлень М й повинні бути безпомилково передані декодеру. Передавальна сторона подає порожній контейнер с N (який являє собою послідов - ність із N незалежно й ідентично розподі - лених відліків відповідно до розподілу контейнера р(с) ), секретний ключ k N (кож - ний символ k i, якого незалежно й рівномір - но розподілений по функції р(k) ), і пові - домлення m на вхід кодера.
25 Останній формує стеганограму s N, яка передається одержувачеві по незахищено-му каналу зв'язку. Стеганограма s N перехоплюється й об-робляється порушником з метою руйнуван-ня або видалення повідомлення m. Перекручену порушником стеганогра-му позначимо як, а атакуючий вплив - умовною функцією розподілу .
26 Ця обробка включає, як окремий випа - док, формування перекрученої стеганогра-ми у вигляді , де q N - детерміноване зображення. Основне припущення: порушник знає розподіл усіх змін у стеганосистемі й, влас-тиво, опис стеганосистеми, але не знає ви-користовуваного секретного ключа (прин-цип Керхгофса для систем захисту інфор-мації).
27 Нехай контейнер с, стеганограма s і модифікована порушником стеганограма належать одній множині С ( c, s, ). Декодер одержувача обчислює оцінку первинного схованого повідомлення m. Якщо, то атакуючий зумів зруй - нувати інформацію, яка захищалася стега - нографічною системою. Формально визначимо внесені викрив-лення в стратегіях передавальної сторони й порушника.
28 Це завершує математичний опис стега - носистеми й дозволяє визначити швид - кість безпомилкової передачі для схеми, представленої на рис. 4.2. Визначення 4.1 Функція викривлення, внесеного від - правником повідомлення, являє собою не - негативну функцію Визначення 4.2 Функція викривлення, внесеного ата - куючої стороною, являє собою ненегатив - ну функцію
29 Функція викривлення d 1 обмежена: Крім того, даний захід викривлення си - метричний: для всіх. Виконання рівності означає збіг: c = s.
30 Якщо, то контейнер-результат не відповідає контейнеру-оригіналу. Функції викривлення d i, i = 1,2 поши - рюються на викривлення символьних по c- лідовностей з довжиною блоків N : Назвемо викривлення контейнера c, викликане вбудовуванням у нього сховано-го повідомлення m, викривленням, викли-каним кодуванням, а викривлення, викли-кане атакуючими діями порушника, - викрив -
31 ленням, викликаним атакуючим впливом. Визначення 4.3 Стеганосистема з довжиною блоку N, що приводить до викривлення, виклика- ного кодуванням, рівень якого не пере- вищує А 1, є сукупністю множини прихову- ваних повідомлень М с кількістю елементів (потужністю) |М|, контейнерів C, стегано-грам і ключів K, а також певних на них функцій кодування Е й декодування D. При цьому Е - відображення контейнера c N, по-відомлення m і ключа k N у стеганограму:
32 Це відображення обмежене величиною середнього викривлення A 1, викликаного кодуванням: . (4.1) Відображення - декоду- вальне відображення прийнятої стегано- послідовності й ключа в декодова- ване повідомлення
33 Таким чином, величина А 1 характери- зує максимально припустиму ступінь ви- кривлення контейнера при вбудовуванні в нього приховуваного повідомлення. Незважаючи на те, що дане визначення формальне описує стеганосистеми блоко- вого типу, на практиці воно може бути роз- ширене й на стеганосистеми потокового ти- пу, у яких вікно обробки описується ковз- ним блоком довжиною N.
34 У цьому випадку параметр N стегано- системи може бути названий довжиною ко- дового обмеження стеганосистеми (за ана-логією з безперервними кодами). У більшості випадків викривлення А 1 є малим, оскільки апріорно ухвалюється, що результат вбудовування в контейнер пові- домлення повинен бути непомітним для сторонньої особи (у тому числі й поруш- ника). У стеганосистемах, у яких контейнер являє собою корисний для одержувача ін-
35 формаційний сигнал і якість якого необ-хідно зберегти, величина А 1 обмежується. У системах ЦВЗ вимога мінімізації А 1 формулюється як вимога прозорості водя- ного знака, що свідчить про приналежність контейнера. Крім того, визначення обмеження ви- кривлення (4.1) містить усереднення сто- совно розподілу й стосовно рів- номірного розподілу повідомлень. Такий вибір зроблений для зручності, оскільки це дозволяє використовувати класичні поло- ження теорії Шеннона.
36 Розподіл і вибір відображен- ня Е визначають конкретний вид розподілу множини формованих стеганограм. Визначення 4.4 Атакуючий вплив (без пам'яті), що при-водить до викривлення А 2, описується умовною функцією розподілу з множини S до множини такий, що ви- конується умова . (4.2)
37 По визначенню, А 2 є максимальною ве- личиною викривлення стеганограми, вик- ликаного навмисними діями порушника. Фі- зичний зміст обмеження величини А 2 полягає в наступному. У системах ЦВЗ по- рушник, намагаючись вилучити водяний знак із завіреного контейнера, змушений сам зменшувати величину А 2, щоб суттєво не спотворити коштовний для нього кон- тейнер. В інших стеганосистемах величина А 2 обмежується наявним у атакуючого енергетичним потенціалом установлення перешкод, що виникають перешкодами для
38 інших каналів зв'язку при використанні за- гального ресурсу й іншими причинами. Логічно припустити, що для реальних стеганосистем звичайно виконується спів-відношення А 2 > А 1. Відповідно до визначення 4.4 вплив, що атакує, описується й обмежується усе-редненими викривленнями між множинами й. В інших випадках, якщо атакуючий знає опис функції Е, той атакуючий вплив описується й обмежується усередненим викривленням між множинами С й :
39 . (4.3) Визначення A 2 відповідно до виразу (4.3) допускає, що порушникові відомі точні імовірнісні характеристики контейнерів. Як буде показана далі, ця обставина істотна ускладнює завдання забезпечення захище- ності приховуваної інформації, тому в стійких стеганосистемах використовуються різні методи приховання від порушника ха- рактеристик використовуваних контейне- рів. Наприклад, такі методи включають ви- користання для вбудовування підмножини
40 контейнерів з імовірнісними характеристи- ками, що відрізняються від характеристик усієї множини відомих порушникові кон- тейнерів, або рандомізовану компресію сигналу контейнера перед вбудовуванням у нього приховуваного повідомлення. Тому обчислення викривлення А 2 відповідно до визначення (4.4) є більш універсальним, оскільки порушник завжди має можливість вивчати імовірнісні характеристики спосте-режуваних стеганограмм. Маючи опис стеганосистеми й атакую- чого впливу, можна описати
41 між передавальної й атакуючої сторонами. Визначення 4.5 Інформаційне-приховувачі дії, що при-водять до викривлень ( А 1,А 2 ), описується взаємозв’язком використаної стеганосис- теми, яка викликає викривлення кодування А 1 и атакуючого впливу, якій викликає вик- ривлення А 2. Швидкість передачі схованих повідомлень по стеганоканалу визначаєть- ся у вигляді . При цьому швидкість передачі R вира-жається через середню кількість біт прихо-
42 вуваного повідомлення, які безпомилково передаються (переносяться) одним симво- лом (пікселем, відліком) стеганопослідов- ності s N. Це визначення співзвучне "класично-му" визначенню швидкості передачі зви- чайних повідомлень по каналу відкритого зв'язку, який виражається в середній кіль- кості безпомилково переданих біт за одне використання каналу. Імовірність руйнування схованого по- відомлення (середню ймовірність помилки) у стеганопослідовності довжиною N визна-
43 чають як (4.4) де приховувані повідомлення m рівномірно вибираються з множини М. Імовірність є усередненою на множині всіх повідомлень імовірністю того, що ата- куючий успішно спотворить сховане пере- дане повідомлення. Атакуючий досягає ус- піху в інформаційному змаганні, якщо деко- доване під час приймання повідомлення не збігається із вбудованим у контейнер при- ховуваним повідомленням, або ж декодер
44 нездатний прийняти однозначний розв'я-зок. Теоретично досяжну швидкість безпо-милкової передачі приховуваних повідом-лень і сховану пропускну здатність при викривленнях не більш, ніж ( А 1, A 2 ) пропо- нується визначити в такий спосіб. Визначення 4.6 Швидкість R безпомилкової передачі приховуваних повідомлень є досяжною для викривлень не більш, ніж ( А 1,А 2 ), якщо існує стеганосистема з довжиною блоку N, яка приводить до викривлення кодування
45 не більш А 1 на швидкості R N > R, така що при N → ∞ при будь-яких атаках порушника, що приводять до викривлень не більш А 2. Визначення 4.7 Схована пропускна здатність В(А 1,А 2 ) є верхньою межею усіх досяжних швидкос-тей безпомилкової передачі приховуваних повідомлень при викривленнях не більш ( А 1,А 2 ). Таким чином, схована пропускна зда- тність є верхньою межею швидкості безпо- милкової передачі приховуваних даних, при якій викривлення контейнера, виклика-
46 ні вбудовуванням у нього зазначених пові- домлень ( А 1 ) і діями порушника по руйну-ванню цих повідомлень ( А 2 ), не переви-щують заданих величин. Як і пропускна здатність каналів пере- дачі відкритих повідомлень, пропускна здатність каналів передачі приховуваних повідомлень визначається в ідеалізованих умовах, при яких затримка кодуван- ня/декодування нескінченна (тобто N → ∞ ), статистика контейнерів, приховуваних по- відомлень, стеганограм і ключів точно ві- дома, складність побудови стеганосистеми
47 не обмежена. Зовсім очевидно, що така пропускна здатність каналу схованого зв'язку має сенс теоретичної межі, що вказує області, у яких існують і, відповідно, не існують сте- ганосистеми при заданих величинах викри- влень. Відомо, що швидкості реальних систем передачі відкритих повідомлень можуть тільки наближатися до величини пропускної здатності відкритих каналів, причому в міру наближення до неї обчис- лювальна складність реалізації систем передачі зростає спочатку приблизно по
48 лінійній, а потім - по квадратичній і далі по експонентній залежності від довжини блоку кодування N. Цілком імовірно, що аналогічні залеж- ності зростання складності закономірні й для стеганосистем у міру наближення швидкості передачі приховуваних даних до величини схованої пропускної здатності. Це припущення підтверджується наявним досвідом побудови стеганосистем. Відомо, що спроби збільшити швидкість передачі приховуваних даних приводять до істот- ного ускладнення методів приховання інформації.
37
