Слайд 2: Введение
Она изучает только равновесные состояния тел, §§ Введение 02 Термодинамика или общая теория теплоты, изучает общие свойства макроскопических систем, отвлекаясь от микроскопического строения вещества (энергетический подход). – равновесные состояния, непрерывно следующие друг за другом. а также медленные процессы
Слайд 3
03 Молекулярная физика изучает строение и свойства вещества, исходя из атомно-молекулярного представления (статистический подход) и рассматривает теплоту как беспорядочное движение атомов и молекул МФ также называют молекулярно- кинетической теорией строения вещества.
Слайд 4
При нормальных условиях 1) В 1 см 3 воздуха содержится 27 000 000 000 000 000 000 = 2,7∙10 19 молекул 2) средняя скорость движения молекул ≈ 500 м/с и она растет с увеличением температуры 3) средняя длина свободного пробега молекул ≈ 10 – 7 м 04 4) за 1 с молекула испытывает около 5 млрд. столкновений
Слайд 5: Термодинамическая система
это совокупность макроскопических тел, обменивающихся энергией между собой и с другими телами Физические величины, характеризующие состояние термодин. системы называются термодинамическими параметрами 05 Любое изменение в системе, связанное с изменением хотя бы одного параметра, называется термодинамическим процессом
Слайд 6
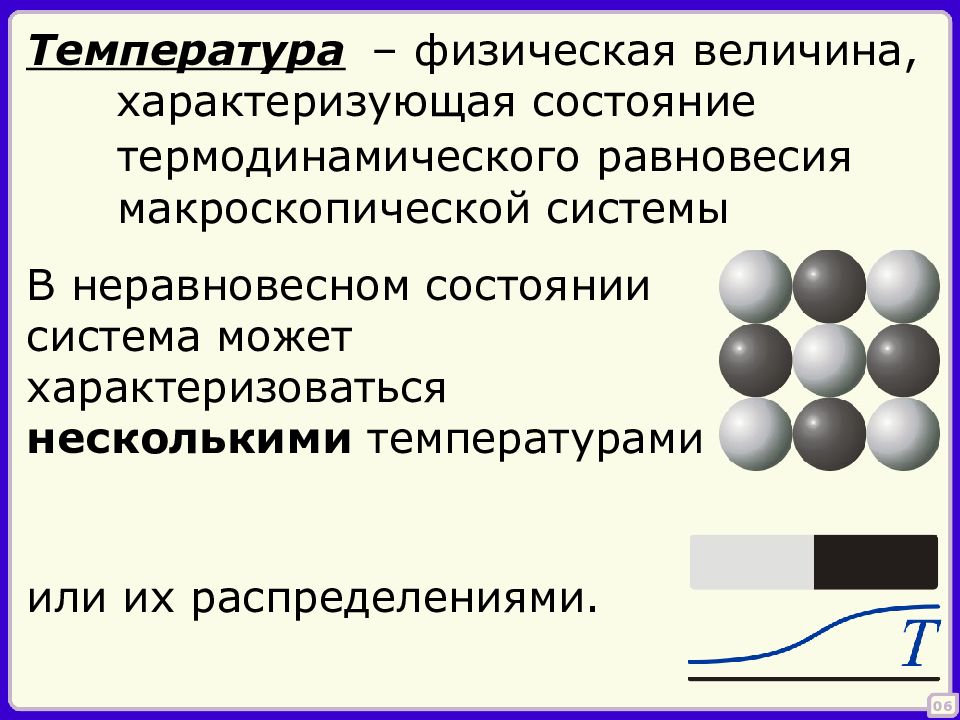
– физическая величина, характеризующая состояние 06 Температура термодинамического равновесия макроскопической системы В неравновесном состоянии система может характеризоваться несколькими температурами или их распределениями.
Слайд 7
07 Давление равная отношению силы, действующей по нормали на некоторую площадку – физическая величина, к величине этой площадки Удельный объем – величина, обратная к плотности если ρ = const, то систему характеризуют общим объемом V
Слайд 8: Уравнение состояния
08 Состояние некоторой массы газа определяется тремя ТД параметрами: p – давление, V – объем, T – температура Уравнение состояния устанавливает связь между ними: или В настоящее время предложено много ( более 100 ) уравнений состояния, различающихся точностью и сложностью
Слайд 9: Идеальный газ
09 это модель среды (как с. м. т. или а. т. т. ), определяемая положениями: 1) суммарный объем молекул газа пренебрежимо мал (по сравнению с объемом сосуда) 2) между молекулами отсутствуют силы взаимодействия 3) столкновения между молекулами и стенкой – абсолютно упругие
Слайд 10
а также при низком давлении и при высокой температуре, 10 Нормальные условия P = 1 атм = 760 мм Hg ≈ 10 5 Па 1,01 3250 ·10 5 Па Техническая атмосфера: 0,98 0665 ·10 5 Па Физическая атмосфера: Температура: T = 273,15 К (0 ° С) Стандартные условия ( химия ) : P = 1 атм, T = 298,15 К (25 ° С) Многие газы при НУ, можно считать идеальными
Слайд 11
11 Уравнение Менделеева–Клапейрона – число молей газа M – молярная масса газа, кг/моль m – масса газа, кг N – число молекул N A = 6,022 · 10 23 – число Авогадро R = 8,31 Дж/(моль∙К)
Слайд 12
12 – концентрация молекул, м – 3 k B = 1,38 ∙10 – 23 Дж/К – постоянная Больцмана Замечание Уравнение Менделеева–Клапейрона оказывается справедливым только при малой плотности реального газа
Слайд 13
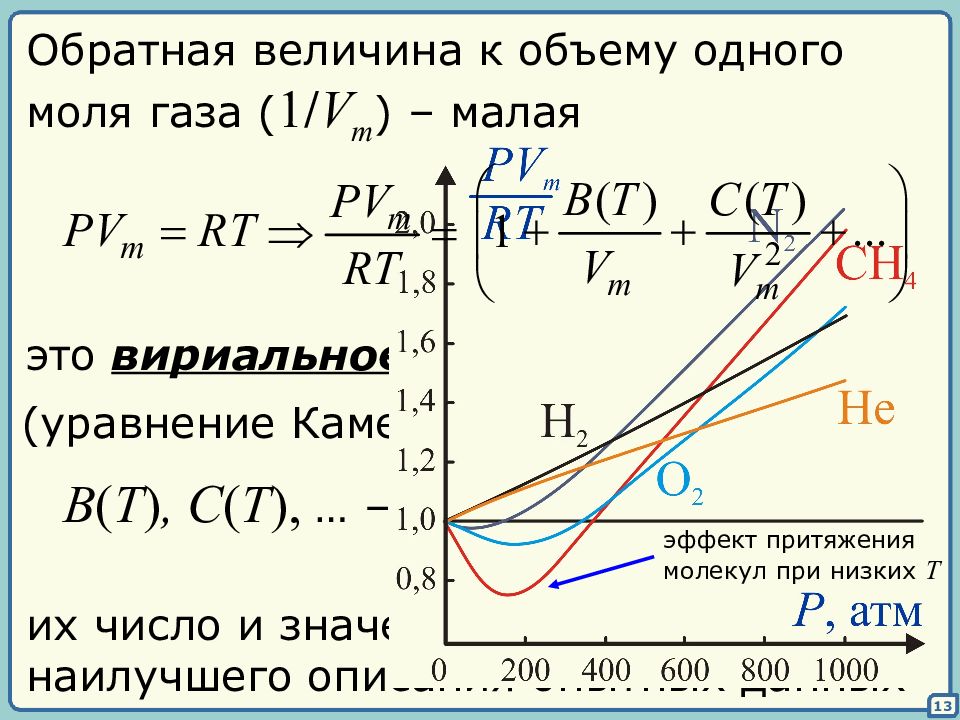
13 Обратная величина к объему одного моля газа ( 1 / V m ) – малая это вириальное уравнение состояния (уравнение Камерлинг-Оннеса, 1901) B ( T ), C ( T ), … – вириальные коэффициенты их число и значения выбирают для наилучшего описания опытных данных эффект притяжения молекул при низких T
Слайд 14: Барометрическая формула
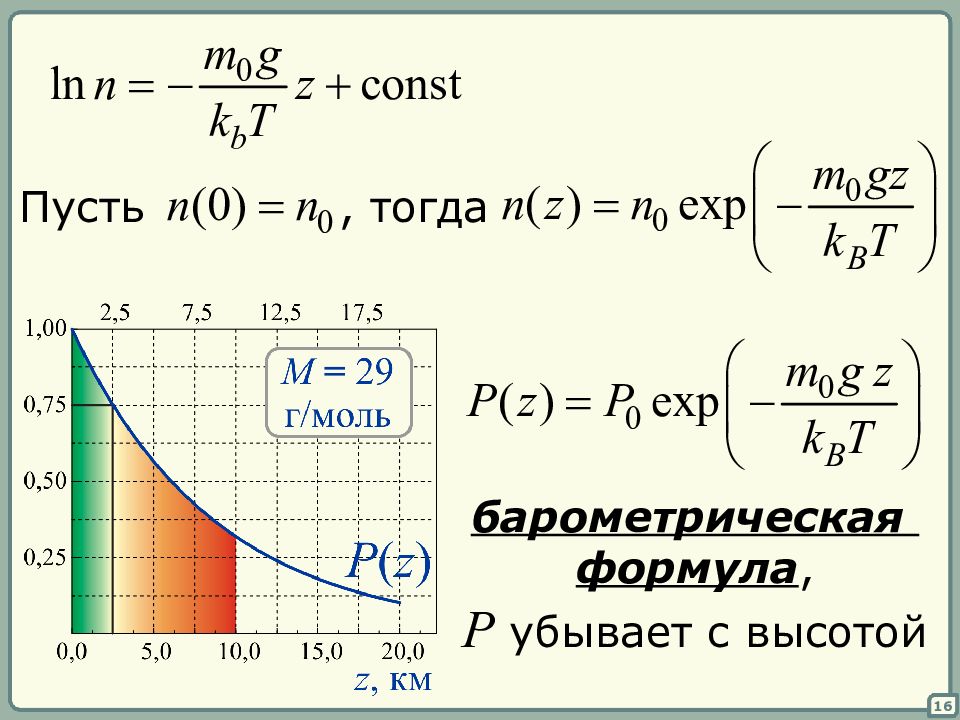
14 Если на газ в сосуде действует сила, то концентрация молекул установится в результате действия «противоположных» факторов: 1) внешнее воздействие 2) хаотическое движение молекул Пусть на газ действует сила тяжести, которая не меняется с высотой. Пусть температура газа постоянна.
Слайд 15
15 Пусть – площадь основания – масса одной молекулы вычислим интеграл от обеих частей
Слайд 17
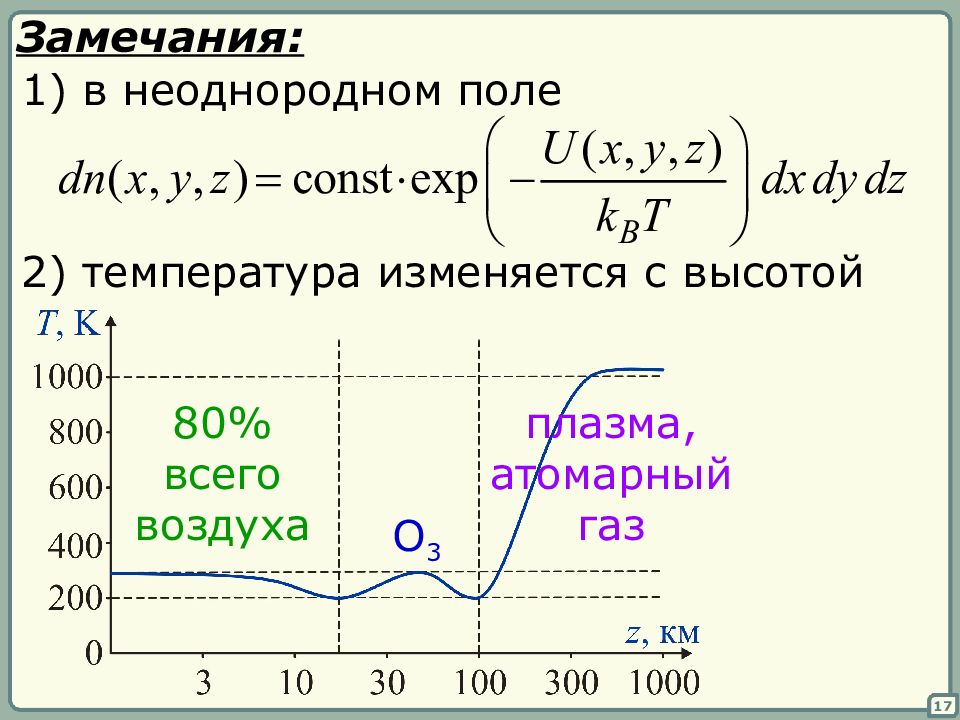
17 Замечания: 1) в неоднородном поле 2) температура изменяется с высотой 80% всего воздуха плазма, атомарный газ O 3
Слайд 18: Учет объема молекул
18 На очень малых расстояниях между молекулами действуют силы отталкивания N – число молекул V – объем сосуда V min – объем всех молекул ( эффективный ) V – V min – объем, доступный для движения молекул
Слайд 19
19 Основное уравнение МКТ: или Пусть b – минимальный объем 1 моля ( объемная поправка ) тогда – уравнение Дюпре
Слайд 20
20 Величина b обычно принимает значения 15 – 60 см 3 /моль Газ b, см 3 / моль Ne 17,09 He 23,70 H 2 26,61 NO 27,89 H 2 O 30,49 O 2 31,83 Ar 32,19 NH 3 37,07 N 2 39,13 Kr 39,78 CO 39,85 CO 2 42,67 CH 4 42,78 NO 2 44,24 Xe 51,05 Cl 2 56,22 SO 2 56,36 C 2 H 6 63,80 C 3 H 8 84,45 При увеличении температуры b уменьшается вместе с радиусом зоны ограждения. Например, в 1 м 3 воздуха при н.у. содержится ≈ 40 моль газа и собственный объем молекул ≈ 1,4 литра ( 0,14 % ) d ≈ 10 – 9 –10 – 10 м
Слайд 21: Внутреннее давление
21 На больших расстояниях между молекулами действуют силы притяжения В центре – практически уравновешены. Вблизи стенки – сила направлена к центру. Следовательно, давление реального газа выше давления идеального газа, но на стенку такой газ оказывает меньшее давление.
Слайд 22
22 Пусть x – расстояние от стенки сосуда, U ( x ) – потенциальная энергия молекулы согласно распределению Больцмана – концентрация молекул в точке, где U = U min = 0 ( центр объема ) Давление газа на стенку ( x = 0 ) :
Слайд 23
23 Концентрация молекул возле стенки V – объем сосуда Тогда Сила, действующая на пристеночную молекулу пропорциональна числу молекул газа N , и, следовательно, U 0 – тоже
Слайд 24
24 a – константа для данного газа – уравнение Дитеричи Если, то He H 2 N 2 O 2 Ar Ne Cl 2 CO 2 H 2 O a, 10 –3 Па·м 6 /моль 2 34 24 135 136 134 209 650 361 554 ≈
Слайд 26
26 P – давление газа на стенку сосуда – внутреннее давление – давление газа при исчезновении сил притяжения между молекулами. При пренебрежении внутренним давлением и объемной поправкой оно переходит в уравнение
Слайд 27: Изобары реального газа
27 Каждый реальный газ представляет собой ненасыщенный (перегретый) пар, т.е. при соответствующем понижении температуры он конденсируется, превращаясь в жидкость или кристалл Рассмотрим воду, налитую в сосуд, закрытый подвижным поршнем ( P = const ) Будем подводить теплоту, начиная с T = 273 K ( 0 ° С )
Слайд 28
28 А : жидкость, T = 273 K A-B : расширение жидкости при нагревании При дальнейшем подведении тепла вода начинает испаряться (т. В, T = 3 73 K ) и объем, занятый водой и паром начинает быстро расти. Температура, при этом, остается постоянной (изотерма = изобаре)
Слайд 29
29 C : T = 373 K В сосуде – жидкость и влажный пар (содержит капельки жидкости, увлеченные с поверхности) D : T = 373 K Это точка конденсации пара. В сосуде – сухой насыщенный пар (капелек не содержит) E : При дальнейшем увеличении температуры пар становится ненасыщенным (перегретым)
Слайд 30
– фазовые переходы I -го рода, сопровождающиеся поглощением или выделением теплоты, 30 Кипение и конденсация изменением состояния и объема. Теплота, выделяющаяся при ФП I- го рода ( скрытая теплота ) – энергия, равная отрицательной потенциальной энергии притяжения молекул Замечание о критической точке Чем больше давление, тем больше расширяется жидкость, прежде чем закипеть (участок АВ ).
Слайд 31
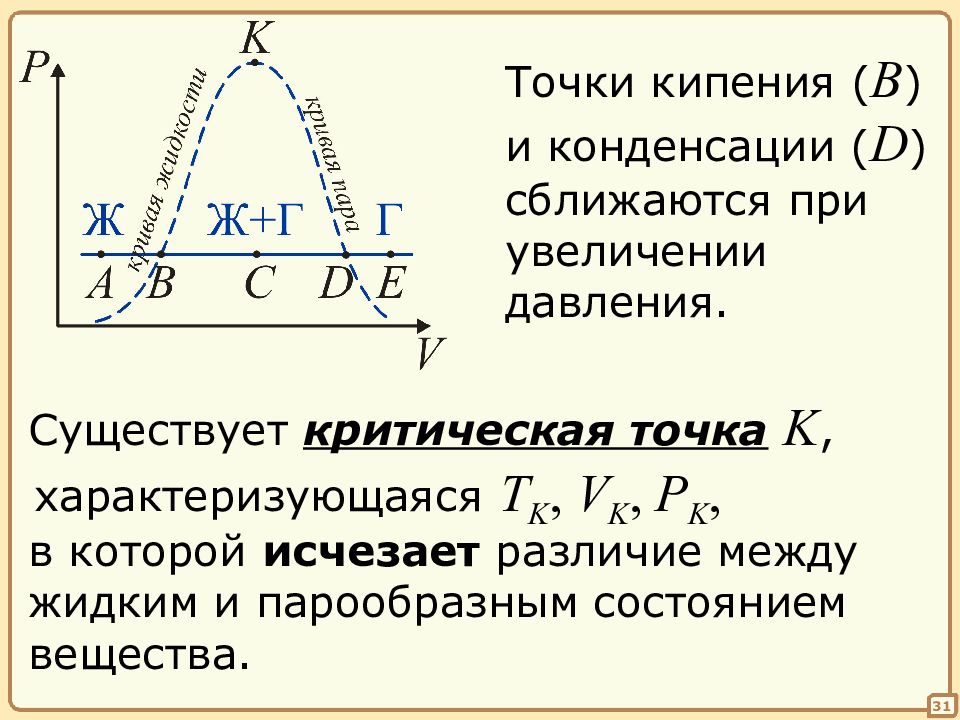
31 Точки кипения ( B ) и конденсации ( D ) сближаются при увеличении давления. Существует критическая точка K, характеризующаяся T K, V K, P K, в которой исчезает различие между жидким и парообразным состоянием вещества.
Слайд 32: Изотермы реального газа
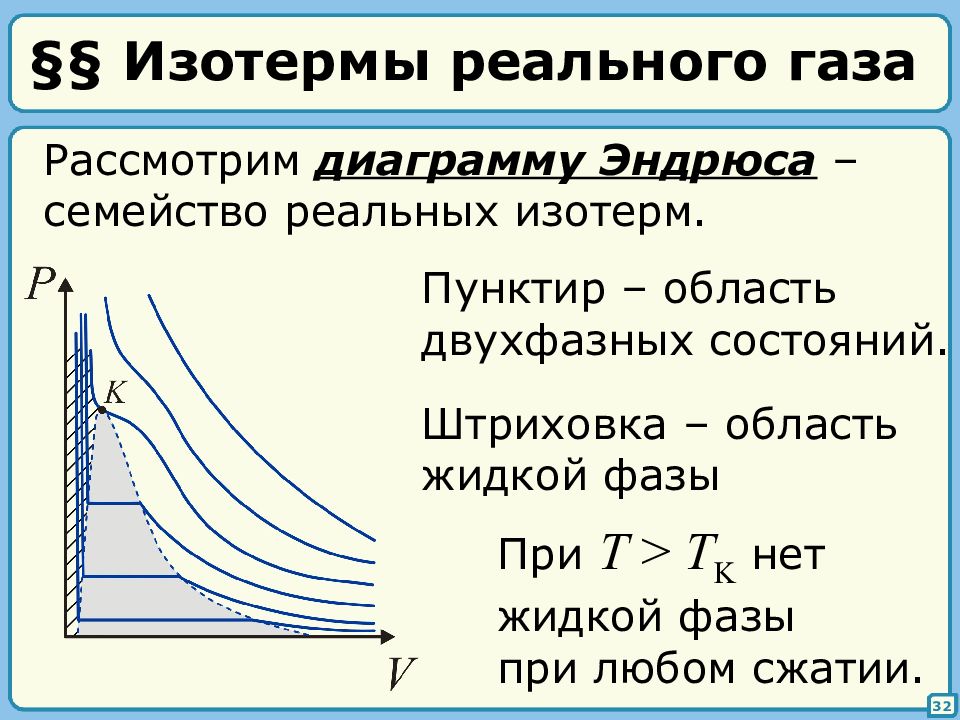
32 Рассмотрим диаграмму Эндрюса – семейство реальных изотерм. Штриховка – область жидкой фазы Пунктир – область двухфазных состояний. При T > T K нет жидкой фазы при любом сжатии.
Слайд 33
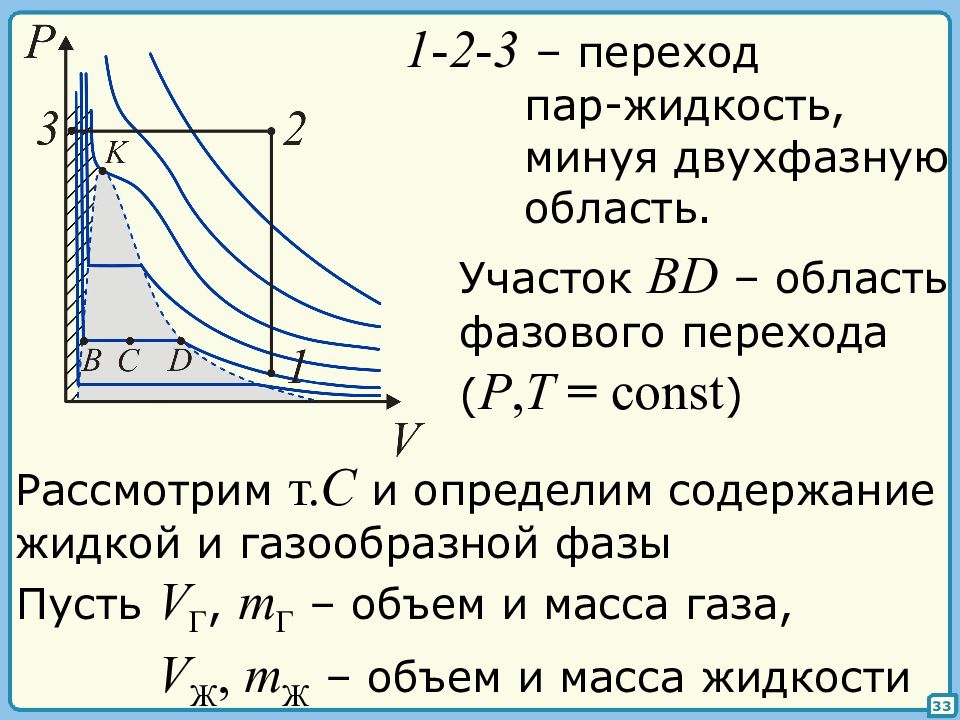
33 1 - 2 - 3 – переход пар-жидкость, минуя двухфазную область. Участок BD – область фазового перехода ( P, T = const ) Рассмотрим т. C и определим содержание жидкой и газообразной фазы Пусть V Г, m Г – объем и масса газа, V Ж, m Ж – объем и масса жидкости
Слайд 34
34 V Г V Ж Тогда ( т.к. эта функция должна быть линейной и в крайних точках совпадать с V B и V D ) или – правило рычага
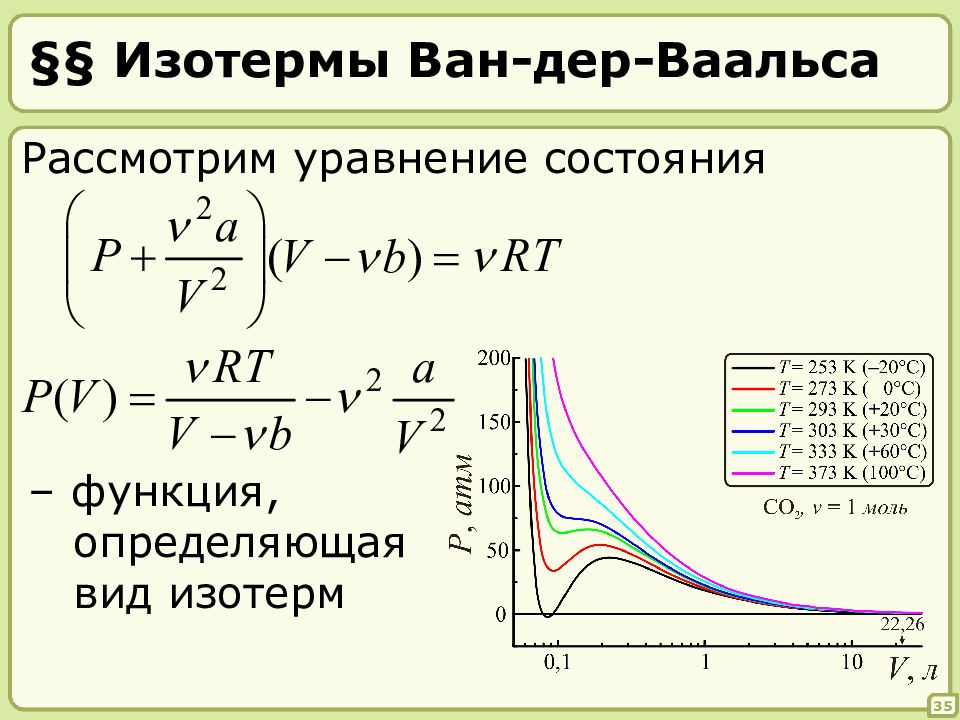
Слайд 35: Изотермы Ван-дер-Ваальса
35 Рассмотрим уравнение состояния – функция, определяющая вид изотерм
Слайд 36: Об уравнениях состояния
36 §§ Об уравнениях состояния Для описания состояния газа в широком интервале P, V, T необходимо пользоваться таблично заданным УС. Для функциональной зависимости требуется не менее 5 индивидуальных параметров. Из рассмотренных уравнений наиболее точными являются вириальное и уравнение Дитеричи.
Слайд 37
37 Уравнение ВДВ хорошо описывает состояние газа при низком давлении и T > T K Для сжатых газов уравнение оправдано в немногих случаях ( CO 2, N 2, этилен) Поведение плотных газов и жидкостей оно описывает только качественно. Для описания существенных сторон физических явлений мы будем использовать только уравнение Менделеева–Клапейрона.
Слайд 38: Степени свободы молекулы
38 Число независимых координат, полностью определяющих положение тела в пространстве, называется числом степеней свободы. Пусть атомы в молекуле не располагаются на одной прямой и связи между ними не жесткие Рассмотрим многоатомную молекулу
Слайд 39
39 колебательные степени свободы Поскольку положения N атомов в молекуле определяют 3 N координат, то i кол = 3 N – ( i пост + i вращ ) i пост = 3 i вращ = 3 Энергия молекулы:
Слайд 40
40 гипотеза Больцмана (з-н Максвелла) в т.с., находящейся в состоянии равновесия, на каждую поступательную и вращательную степень свободы приходится энергия ½ k B T и k B T – на каждую колебательную. Средняя энергия молекулы: i = i пост + i вращ + 2 i кол
Слайд 41
41 Пример : одноатомная молекула (только поступ. движение) Пример : двухатомная молекула с жесткой связью – вращением относительно оси x можно пренебречь
Слайд 42
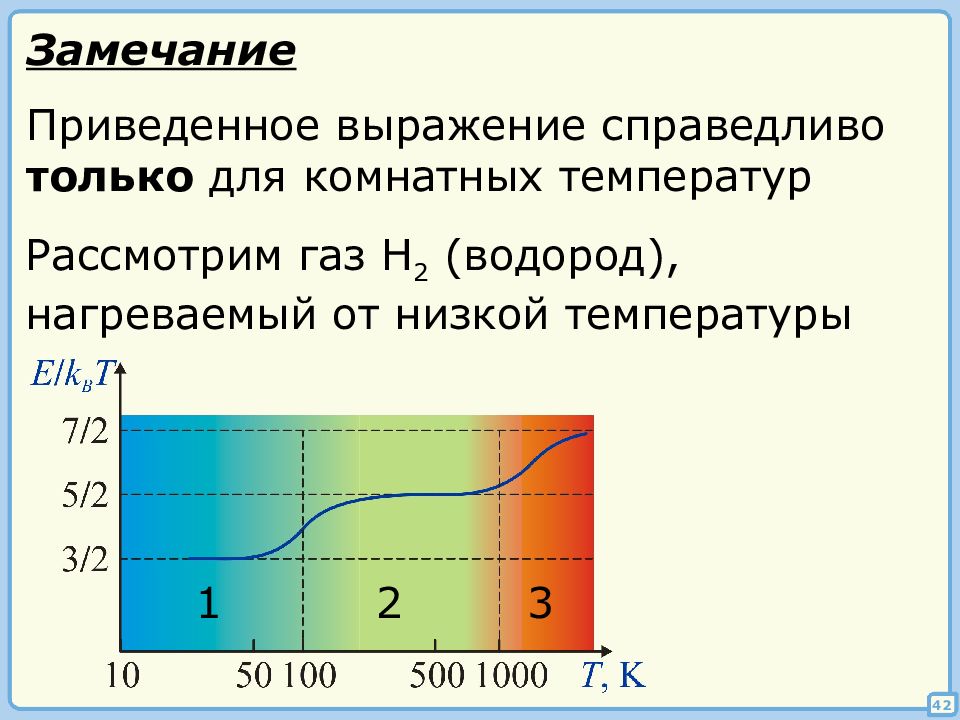
42 Приведенное выражение справедливо только для комнатных температур Рассмотрим газ H 2 (водород), нагреваемый от низкой температуры 1 2 3 Замечание
Слайд 43
1 ) Для молекулы, состоящей из любого числа атомов, i = 3. Для возбуждения вращательной степени свободы молекулам необходима некоторая минимальная энергия 2 ) В газе есть молекулы с i = 3 и i = 5. (вращательные уровни «разморожены») 3 ) Энергии достаточно для возбуждения колебательных степеней свободы, но диссоциация наступает раньше, чем их полное «размораживание» 43
Слайд 44: Средняя скорость молекул
46 Средняя кинетическая энергия молекулы Средняя квадратичная скорость Средняя арифметическая скорость
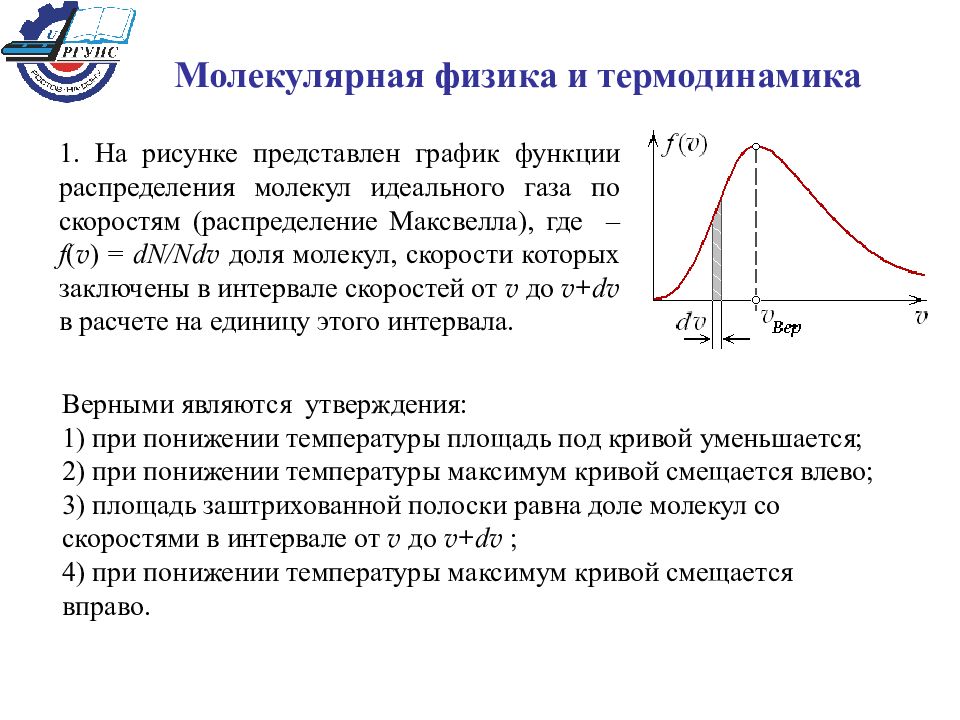
Слайд 45: Распределение Максвелла
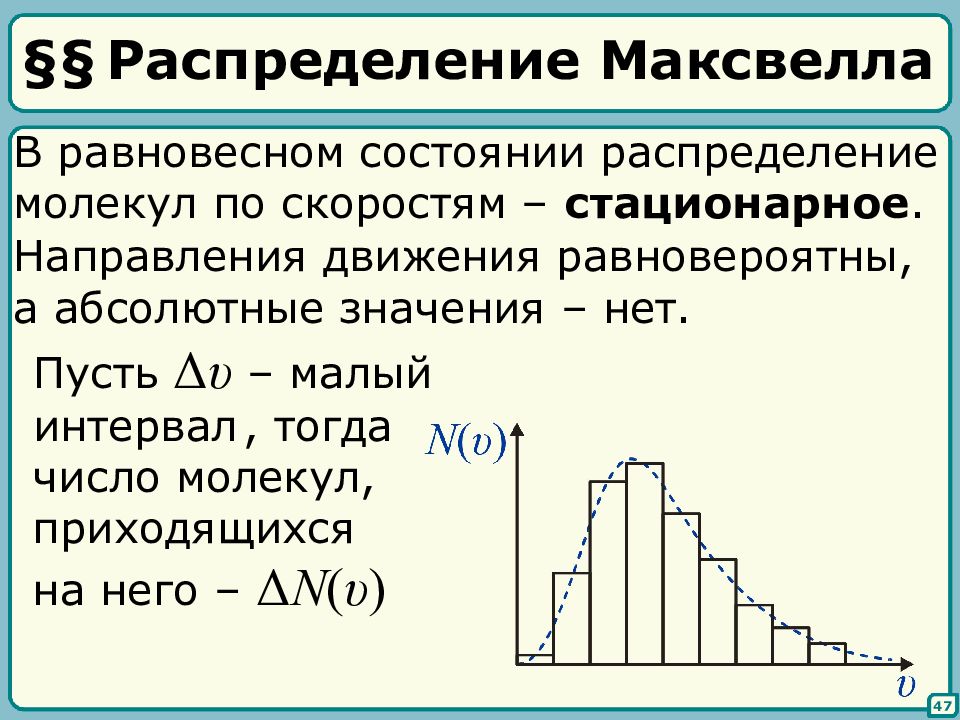
47 В равновесном состоянии распределение молекул по скоростям – стационарное. Направления движения равновероятны, а абсолютные значения – нет. Пусть Δ υ – малый интервал , тогда число молекул, приходящихся на него – Δ N ( υ )
Слайд 46
48 – функция распределения молекул по скоростям – относительное число молекул со скоростями в интервале – функция распределения Максвелла
Слайд 47
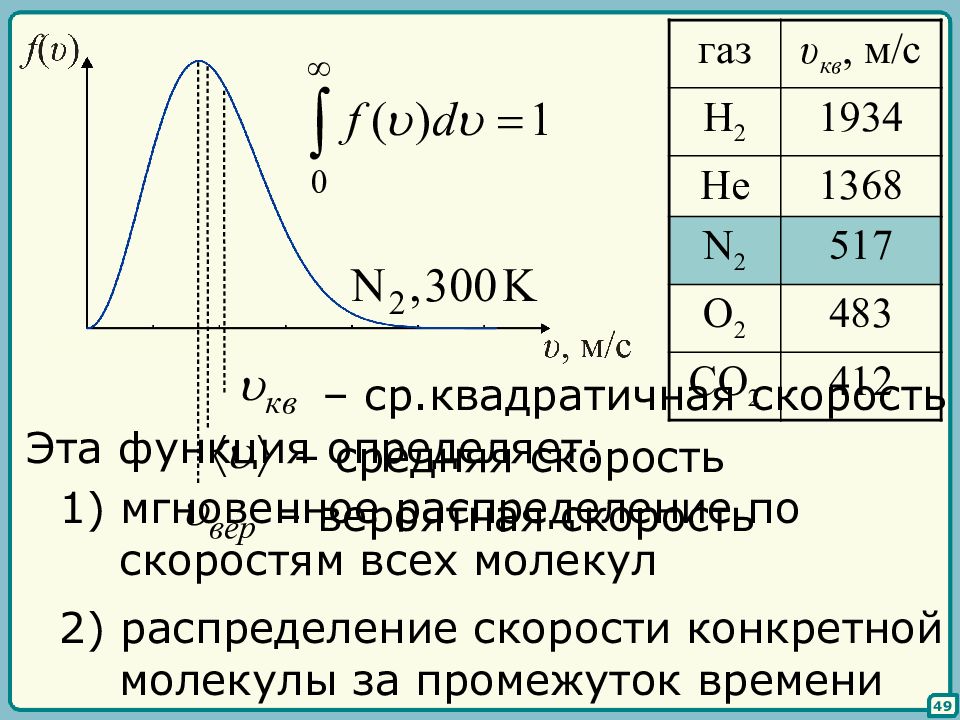
49 – вероятная скорость – средняя скорость – ср.квадратичная скорость Эта функция определяет: 1) мгновенное распределение по скоростям всех молекул 2) распределение скорости конкретной молекулы за промежуток времени газ υ кв, м/с H 2 1934 He 1368 N 2 517 O 2 483 CO 2 412
Слайд 48
(плотность вероятности) иметь молекуле данную скорость 50 Вычислим наиболее вероятную скорость Вычислим среднюю скорость. Учтем, что f ( υ ) – вероятность
Слайд 50
52 вероятная скорость: средняя скорость: ср. квадратичная: Замечание Если в сосуде несколько сортов молекул, то в состоянии равновесия средние энергии у них – одинаковы
Слайд 51: Понятие температуры
53 Распределение молекул по скоростям у разряженного газа, находящегося при высокой температуре описывается законом Максвелла В области низких температур
Слайд 52
54 В этой области часть реальных газов имеет распределение Ферми (кин. энергия у молекул остается и при T = 0 K ) или распределение Бозе (движение замирает раньше, чем T = 0 K ) При повышении температуры они стремятся к распределению Максвелла область вырождения
Слайд 53
55 Понятие температуры сейчас не имеет наглядного молекулярно-кинетического представления. До создания квантовой теории, понятие температуры было одним из самых простых, а сейчас – одно из наиболее сложных. Под температурой следует понимать величину, которая устанавливается независимо от представлений об идеальном газе.
Слайд 54: Длина свободного пробега
, n – концентрация 44 – средняя скорость молекулы Пусть z – число соударений за время Δ t, тогда все эти молекулы находились в объеме ломанного цилиндра Пусть d – эффективный диаметр молекулы ( d ~ 2–3 Å )