Слайд 2
Применение первого начала к изопроцессам в идеальном газе. Уравнение адиабаты и политропы.
Слайд 3: Первое начало термодинамики
Допустим, что некоторая система (газ, заключенный в цилиндр под поршнем), обладая внутренней энергией U 1, получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией U 2, совершила работу А над внешней средой, т. е. против внешних сил. Количество теплоты считается положительным, когда оно подводится к системе, а работа — положительной, когда система совершает ее против внешних сил. Опыт показывает, что в соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во второе изменение внутренней энергии будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой А, совершенной системой против внешних сил: или
Слайд 4: Первое начало термодинамики
Последнее уравнение выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Выражение в дифференциальной форме будет иметь вид или в более корректной форме где ( dU — бесконечно малое изменение внутренней энергии системы, - элементарная работа, - бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, и таковыми не являются.
Слайд 5: Первое начало термодинамики
Из формулы Q = ΔU+A следует, что в СИ количество теплоты выражается в тех же единицах, что работа и энергия, т. е. в джоулях (Дж). Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии Тогда, согласно первому началу термодинамики, т. е. вечный двигатель первого рода —периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия,— невозможен (одна из формулировок первого начала термодинамики).
Слайд 6: Первое начало термодинамики
Первый закон термодинамики является обобщением закона сохранения и превращения энергии с учетом процессов теплообмена. Принципиальное отличие первого начала ТД от аналогичного закона в механике состоит в учете величины Q – тепловой энергии. Изучение этой величины и ее превращений и есть предмет ТД
Слайд 7: Первое начало термодинамики
Q = ΔU + A Количество теплоты, полученное системой, идет на изменение ее внутренней энергии ΔU = U 2 -U 1 и совершение работы над внешними телами. Так же как в механике этот закон не может предсказать направление развития процесса. Он позволяет только указать возможен ли данный процесс и как в нем изменяются величины Q, U, A.
Слайд 10: Применение первого начала термодинамики к изопроцессам
Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным. Изохорный процесс ( V = const ). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис.), где процесс 1—2 есть изохорное нагревание, а 1—3 изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.
Слайд 11: Применение первого начала термодинамики к изопроцессам
Как уже указывалось, из первого начала термодинамики для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: Согласно формуле, для моля газа Тогда для произвольной массы газа получим
Слайд 15: Применение первого начала термодинамики к изопроцессам
Изобарный процесс ( p = const ). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при расширении объема от V 1 до V 2 равна и определяется площадью прямоугольника, выполненного в цвете на рис.
Слайд 16: Применение первого начала термодинамики к изопроцессам
Если использовать уравнение Клапейрона Менделеева для выбранных двух состояний, то откуда Тогда выражение для работы изобарного расширения примет вид
Слайд 17: Применение первого начала термодинамики к изопроцессам
Из этого выражения вытекает физический смысл молярной газовой постоянной R : если T 2 - T 1 = 1 К, то для 1 моля газа R = А, т. е. R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К. В изобарном процессе при сообщении газу массой m количества теплоты его внутренняя энергия возрастает на величину При этом газ совершит работу, определяемую выражением
Слайд 20: Применение первого начала термодинамики к изопроцессам
Изотермический процесс (Т= const ). Как уже указывалось, изотермический процесс описывается законом Бойля — Мариотта: Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу (см. рис.), расположенную на диаграмме тем выше, чем выше температура, при которой происходил процесс. Найдем работу изотермического расширения газа:
Слайд 21: Применение первого начала термодинамики к изопроцессам
Так как при T= const внутренняя энергия идеального газа не изменяется: то из первого начала термодинамики следует, что для изотермического процесса т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
Слайд 22: Применение первого начала термодинамики к изопроцессам
Следовательно, для того чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.
Слайд 26: Адиабатический процесс
Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д.
Слайд 27: Адиабатический процесс
Из первого начала термодинамики для адиабатического процесса следует, что т. е. внешняя работа совершается за счет изменения внутренней энергии системы. Используя выражения и, для произвольной массы газа перепишем уравнение в виде
Слайд 28: Адиабатический процесс
Продифференцировав уравнение состояния для идеального газа получим Исключим из и последнего ур-я температуру Т. (Разделим одно на второе)
Слайд 30: Адиабатический процесс
Разделив переменные и учитывая, что найдем Интегрируя это уравнение в пределах от p 1 до р 2 и соответственно от V 1 до V 2, а затем потенцируя, придем к выражению или
Слайд 31: Адиабатический процесс
Так как состояния 1 и 2 выбраны произвольно, то можно записать Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона. Для перехода к переменным Т, V или р, Т исключим с помощью уравнения Клапейрона — Менделеева соответственно давление или объем:
Слайд 32: Адиабатический процесс
Выражения представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов ( Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i = 3, γ = 1,67. Для двухатомных газов ( Н 2, N 2, 0 2 и др.) i = 5, γ = 1,4. Значения γ, вычисленные по формуле, хорошо подтверждаются экспериментом.
Слайд 33: Адиабатический процесс
Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой (рис.). На рисунке видно, что адиабата ( pV γ = const ) более крута, чем изотерма ( pV = const ). Это объясняется тем, что при адиабатическом сжатии 1—3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.
Слайд 34: Применение первого начала термодинамики к изопроцессам
Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем уравнение в виде Если газ адиабатически расширяется от объема V 1 до V 2, то его температура уменьшается от T 1 до T 2 и работа расширения идеального газа
Слайд 35: Применение первого начала термодинамики к изопроцессам
Применяя те же приемы, что и при выводе формул ранее, выражение для работы при адиабатическом расширении можно преобразовать к виду где
Слайд 36: Применение первого начала термодинамики к изопроцессам
Работа, совершаемая газом при адиабатическом расширении 1—2 (определяется площадью, выполненной в цвете на рис. ), меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
Слайд 43: Политропный процесс
Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны C V и С p в изотермическом процессе ( dT = 0) теплоемкость равна в адиабатическом теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным.
Слайд 44: Политропный процесс
Исходя из первого начала термодинамики при условии постоянства теплоемкости ( C = const ) можно вывести уравнение политропы: Где n=( C - C p )/( C - C V ) показатель политропы. Очевидно, что при С=0, n = γ получается уравнение адиабаты; при С=, n= 1 —уравнение изотермы; при С=Ср, n = 0 — уравнение изобары, при C = C V, n= —уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.
Слайд 46: Политропный процесс
Исходя из первого начала термодинамики при условии постоянства теплоемкости ( C = const ) можно вывести уравнение политропы: Где n=( C - C p )/( C - C V ) показатель политропы. Очевидно, что при С=0, n = γ получается уравнение адиабаты pV γ =const ; при С=∞, n= 1 —уравнение изотермы pV =const ; при С=С р, n = 0 — уравнение изобары pV 0 =p=const, при C = C V, n= ± ∞ —уравнение изохоры V =const. pV n =const→( pV n ) 1/n =const 1/n → p 1/n V =const 1/n → p 0 V =const→ V =const Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.
Слайд 49: Применение первого закона термодинамики к изопроцессам в газах
В изохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно, Q = ΔU = U(T 2 ) – U(T 1 ). Здесь U(T 1 ) и U(T 2 ) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).
Слайд 50: Применение первого закона термодинамики к изопроцессам в газах
В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением A = p(V 2 – V 1 ) = pΔV. Первый закон термодинамики для изобарного процесса дает: Q = U(T 2 ) – U(T 1 ) + p(V 2 – V 1 ) = ΔU + pΔV. При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T 2 < T 1 ; внутренняя энергия убывает, ΔU < 0.
Слайд 51: Применение первого закона термодинамики к изопроцессам в газах
В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.
Слайд 52: Первый закон термодинамики для изотермического процесса
Первый закон термодинамики для изотермического процесса выражается соотношением Q = A. Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.
Слайд 53: Применение первого закона термодинамики к изопроцессам в газах
Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими. В адиабатическом процессе Q = 0; поэтому первый закон термодинамики принимает вид A = –ΔU, т. е. газ совершает работу за счет убыли его внутренней энергии.
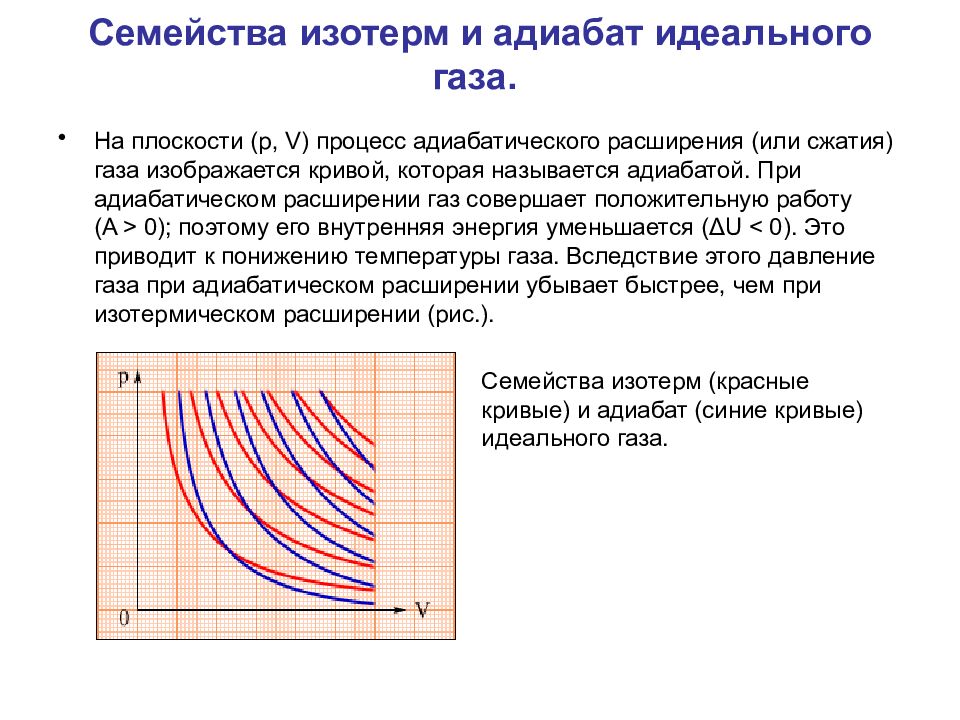
Слайд 54: Семейства изотерм и адиабат идеального газа
На плоскости (p, V) процесс адиабатического расширения (или сжатия) газа изображается кривой, которая называется адиабатой. При адиабатическом расширении газ совершает положительную работу (A > 0); поэтому его внутренняя энергия уменьшается (ΔU < 0). Это приводит к понижению температуры газа. Вследствие этого давление газа при адиабатическом расширении убывает быстрее, чем при изотермическом расширении (рис.). Семейства изотерм (красные кривые) и адиабат (синие кривые) идеального газа.
Слайд 55: Уравнение Пуассона
В термодинамике выводится уравнение адиабатического процесса для идеального газа. В координатах (p, V) это уравнение имеет вид pV γ = const. Это соотношение называют уравнением Пуассона. Здесь γ = C p / C V – показатель адиабаты, C p и C V – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом.
Слайд 56
Для одноатомного газа для двухатомного для многоатомного Работа газа в адиабатическом процессе просто выражается через температуры T 1 и T 2 начального и конечного состояний: A = C V (T 2 – T 1 ).
Слайд 57: Адиабатический процесс
Адиабатический процесс также можно отнести к изопроцессам. В термодинамике важную роль играет физическая величина, которая называется энтропией. Изменение энтропии в каком-либо квазистатическом процессе равно приведенному теплу ΔQ / T, полученному системой. Поскольку на любом участке адиабатического процесса ΔQ = 0, энтропия в этом процессе остается неизменной. Адиабатический процесс (так же, как и другие изопроцессы) является процессом квазистатическим. Все промежуточные состояния газа в этом процессе близки к состояниям термодинамического равновесия. Любая точка на адиабате описывает равновесное состояние.
Слайд 58
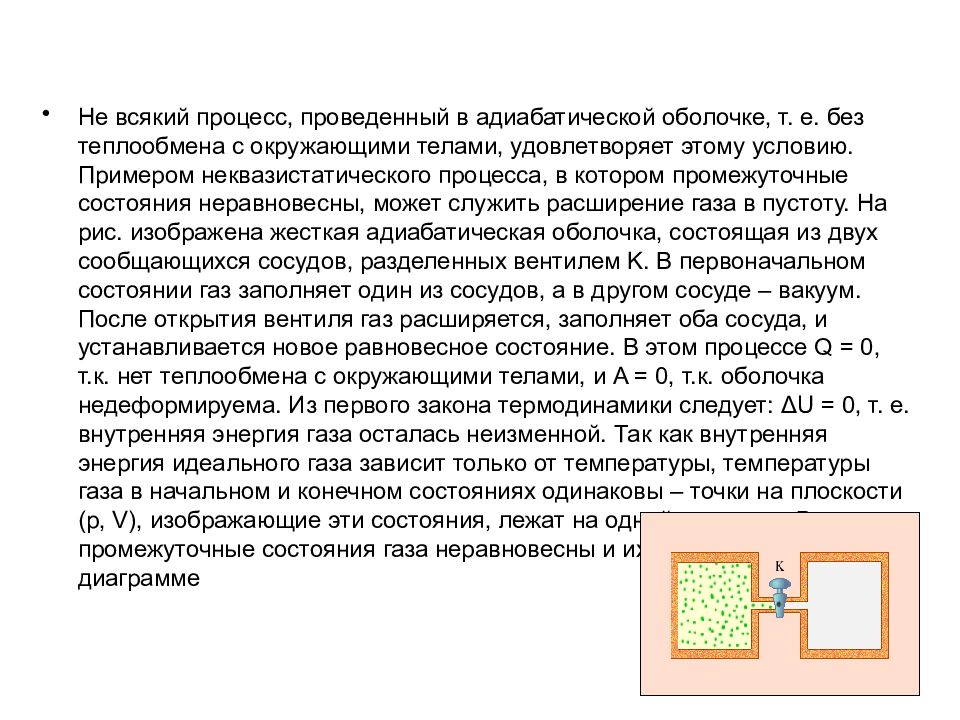
Не всякий процесс, проведенный в адиабатической оболочке, т. е. без теплообмена с окружающими телами, удовлетворяет этому условию. Примером неквазистатического процесса, в котором промежуточные состояния неравновесны, может служить расширение газа в пустоту. На рис. изображена жесткая адиабатическая оболочка, состоящая из двух сообщающихся сосудов, разделенных вентилем K. В первоначальном состоянии газ заполняет один из сосудов, а в другом сосуде – вакуум. После открытия вентиля газ расширяется, заполняет оба сосуда, и устанавливается новое равновесное состояние. В этом процессе Q = 0, т.к. нет теплообмена с окружающими телами, и A = 0, т.к. оболочка недеформируема. Из первого закона термодинамики следует: ΔU = 0, т. е. внутренняя энергия газа осталась неизменной. Так как внутренняя энергия идеального газа зависит только от температуры, температуры газа в начальном и конечном состояниях одинаковы – точки на плоскости (p, V ), изображающие эти состояния, лежат на одной изотерме. Все промежуточные состояния газа неравновесны и их нельзя изобразить на диаграмме
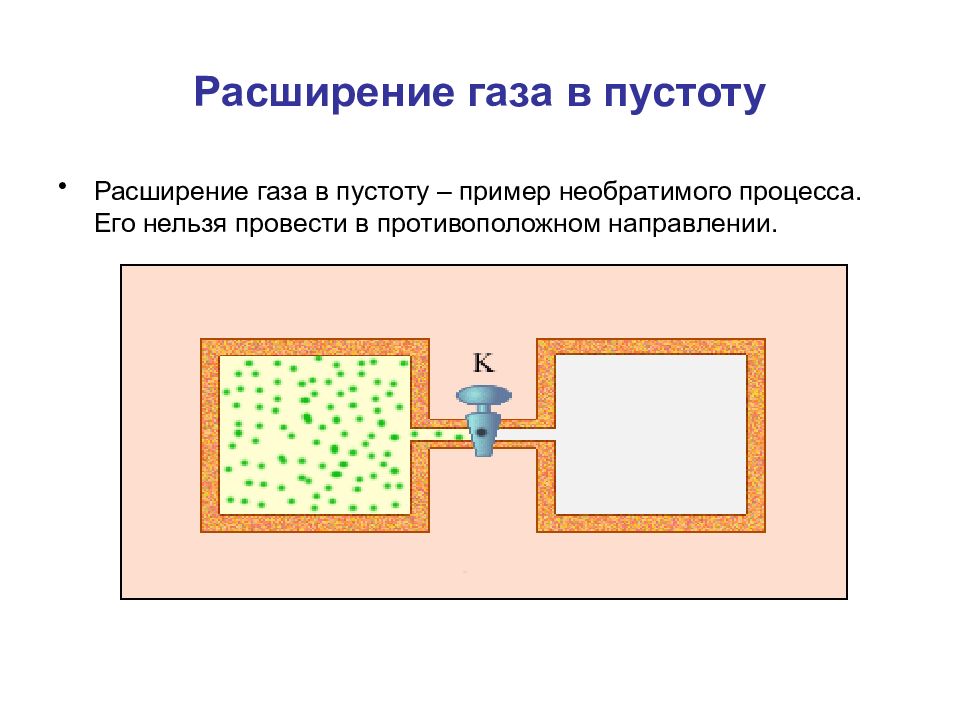
Слайд 59: Расширение газа в пустоту
Расширение газа в пустоту – пример необратимого процесса. Его нельзя провести в противоположном направлении.
Слайд 69: Политропный процесс
Исходя из первого начала термодинамики при условии постоянства теплоемкости ( C = const ) можно вывести уравнение политропы: Где n=( C - C p )/( C - C V ) показатель политропы. Очевидно, что при С=0, n = γ получается уравнение адиабаты pV γ =const ; при С=∞, n= 1 —уравнение изотермы pV =const ; при С=С р, n = 0 — уравнение изобары pV 0 =p=const, при C = C V, n= ± ∞ —уравнение изохоры V =const. pV n =const→( pV n ) 1/n =const 1/n → p 1/n V =const 1/n → p 0 V =const→ V =const Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.