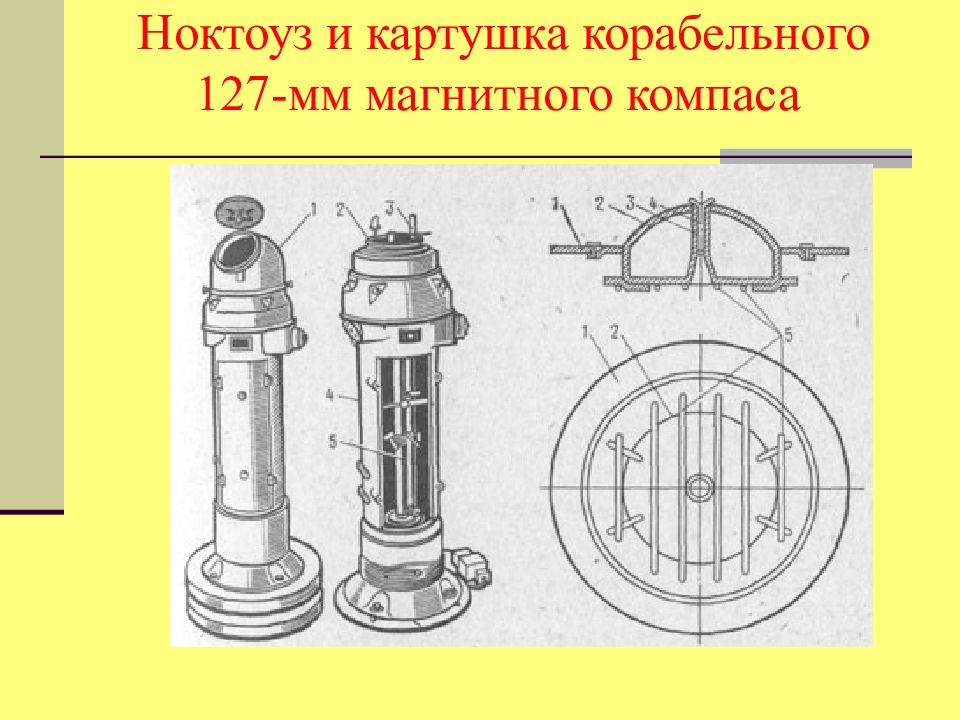
Первый слайд презентации
МОРСКОЙ КОРПУС ПЕТРА ВЕЛИКОГО САНКТ-ПЕТЕРБУРГСКИЙ ВОЕННО-МОРСКОЙ ИНСТИТУТ ОСНОВЫ ПРАКТИЧЕСКОЙ НАВИГАЦИ (Сборник слайдов) Санкт-Петербург 2012 г. А. П. ЗВЕРЕВ
Слайд 2: Основы практической навигации
Учебно-методическое пособие является электронной версией издания «Основ практической навигации» 2001 года и предназначено для курсантов штур - манского факультета, а также препо - давателей кафедры, проводящих занятия по дисциплине «Морская Навигация». Учебное пособие разработано Старшим преподавателем кафедры Доцентом Зверевым А.П.
Слайд 4
Навигация – Наука о выборе пути, определении места и перемещении судна в море с учетом задач, решаемых суд - ном, и влияния внешней среды на направление и скорость суд - на. (ГОСТ 23634-83).
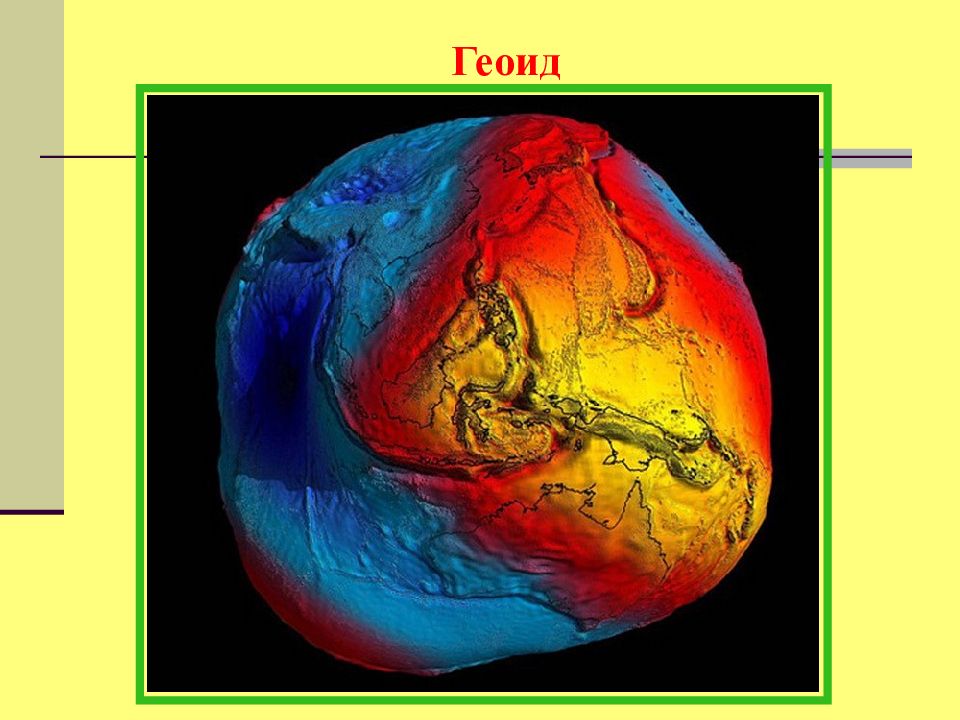
Слайд 6: Геоид
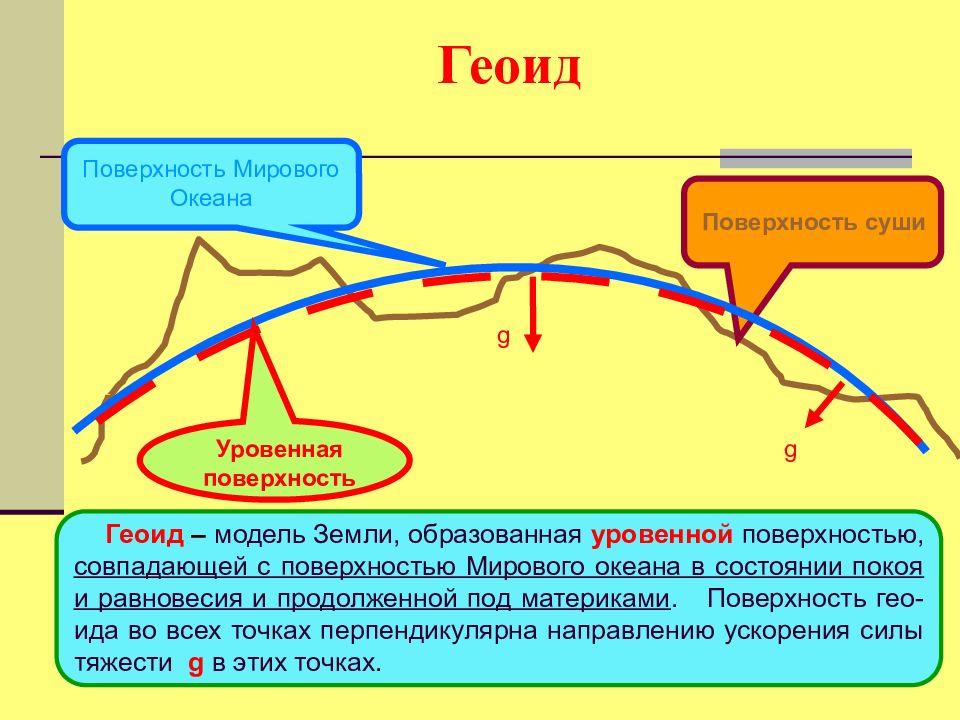
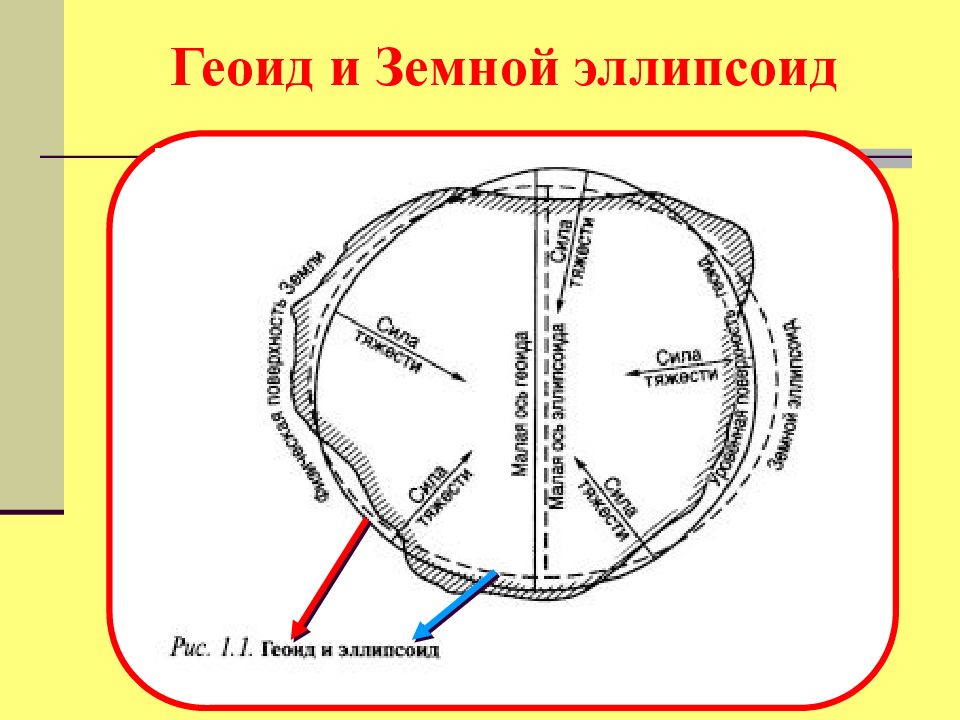
Поверхность суши Поверхность Мирового Океана g g Уровенная поверхность Геоид – модель Земли, образованная уровенной поверхностью, совпадающей с поверхностью Мирового океана в состоянии покоя и равновесия и продолженной под материками. Поверхность гео-ида во всех точках перпендикулярна направлению ускорения силы тяжести g в этих точках.
Слайд 8: Земной эллипсоид (сфероид)
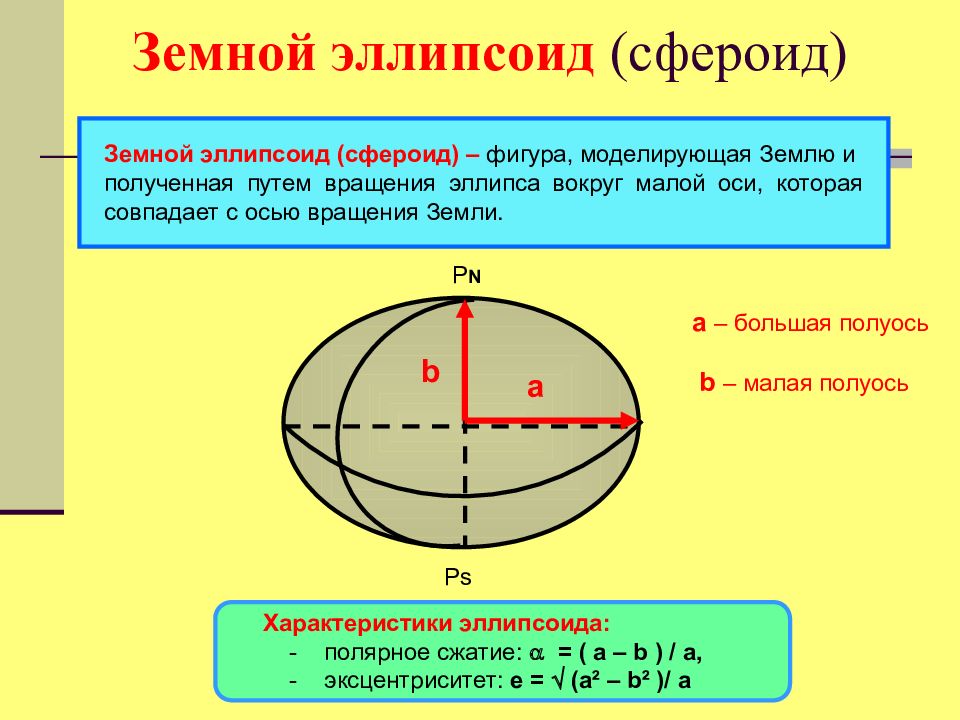
Характеристики эллипсоида: - полярное сжатие: = ( a – b ) / a, - эксцентриситет: e = (a ² – b ² )/ a P N Ps a – большая полуось a b – малая полуось b Земной эллипсоид (сфероид) – фигура, моделирующая Землю и полученная путем вращения эллипса вокруг малой оси, которая совпадает с осью вращения Земли.
Слайд 10
Референц-эллипсоид – земной эллип - соид определенных размеров, приня - тый в государстве в качестве моде - ли Земли. В России – референц -эллипсоид Ф. Н. Красовского, принятый в 1946 году. Характеристики референц-эллипсоида: большая полуось: а = 6378245 м; малая полуось: b = 6356863 м; полярное сжатие = 1 / 298,3.
Слайд 11: Шар
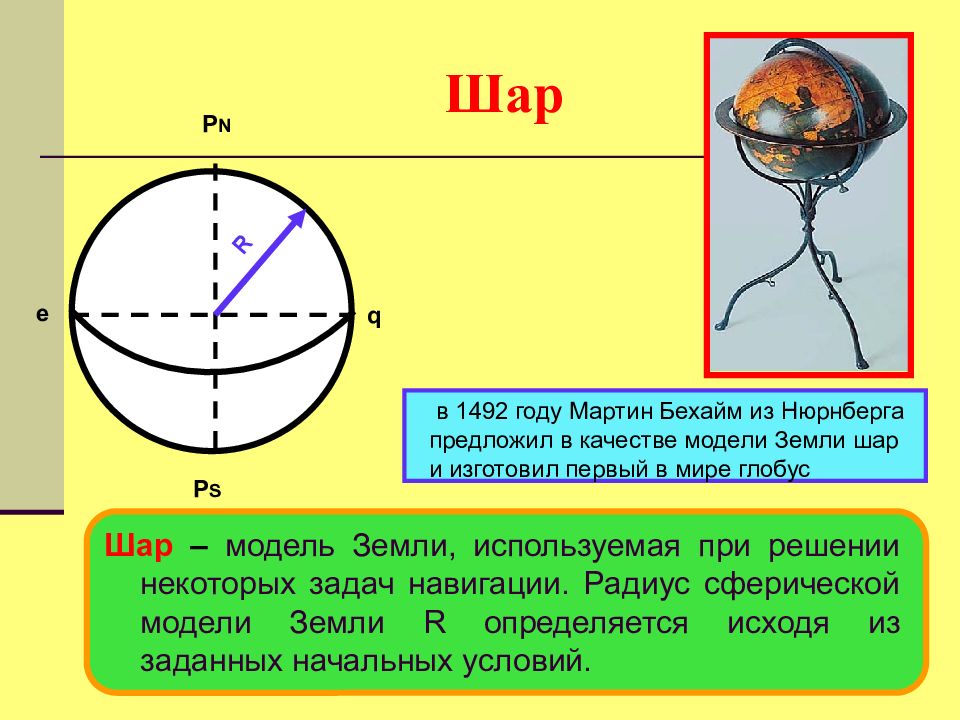
Шар – модель Земли, используемая при решении некоторых задач навигации. Радиус сферической модели Земли R определяется исходя из заданных начальных условий. в 1492 году Мартин Бехайм из Нюрнберга предложил в качестве модели Земли шар и изготовил первый в мире глобус P N P S e q R
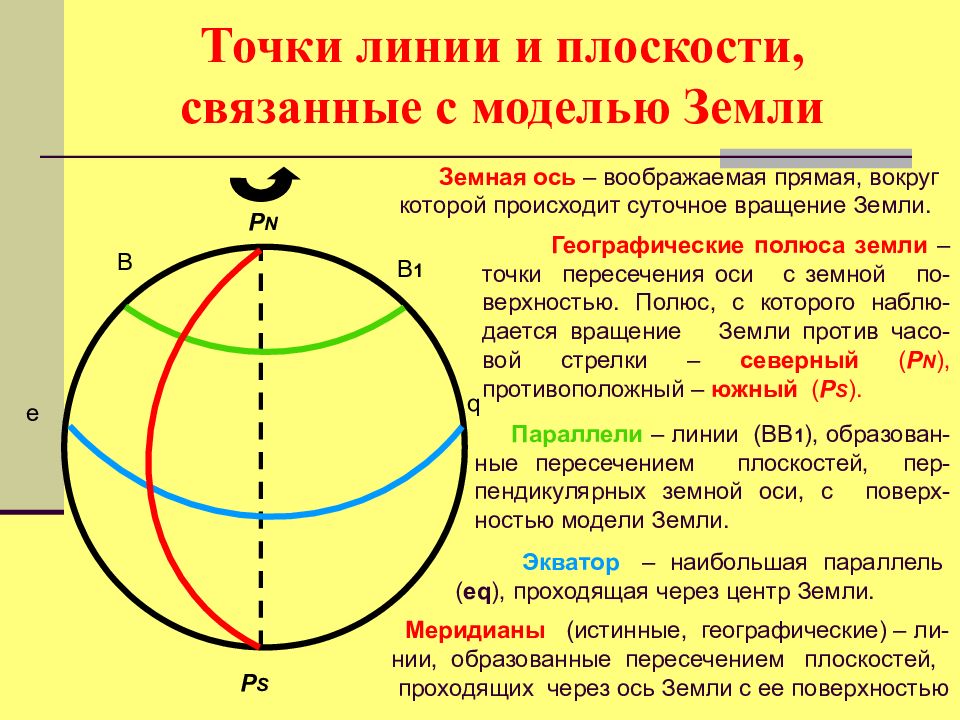
Земная ось – воображаемая прямая, вокруг которой происходит суточное вращение Земли. Географические полюса земли – точки пересечения оси с земной по-верхностью. Полюс, с которого наблю-дается вращение Земли против часо-вой стрелки – северный ( P N ), противоположный – южный ( P S ). P N P S Параллели – линии (ВВ 1 ), образован - ные пересечением плоскостей, пер - пендикулярных земной оси, с поверх - ностью модели Земли. В В 1 Экватор – наибольшая параллель ( eq ), проходящая через центр Земли. е q Меридианы (истинные, географические) – ли - нии, образованные пересечением плоскостей, проходящих через ось Земли с ее поверхностью
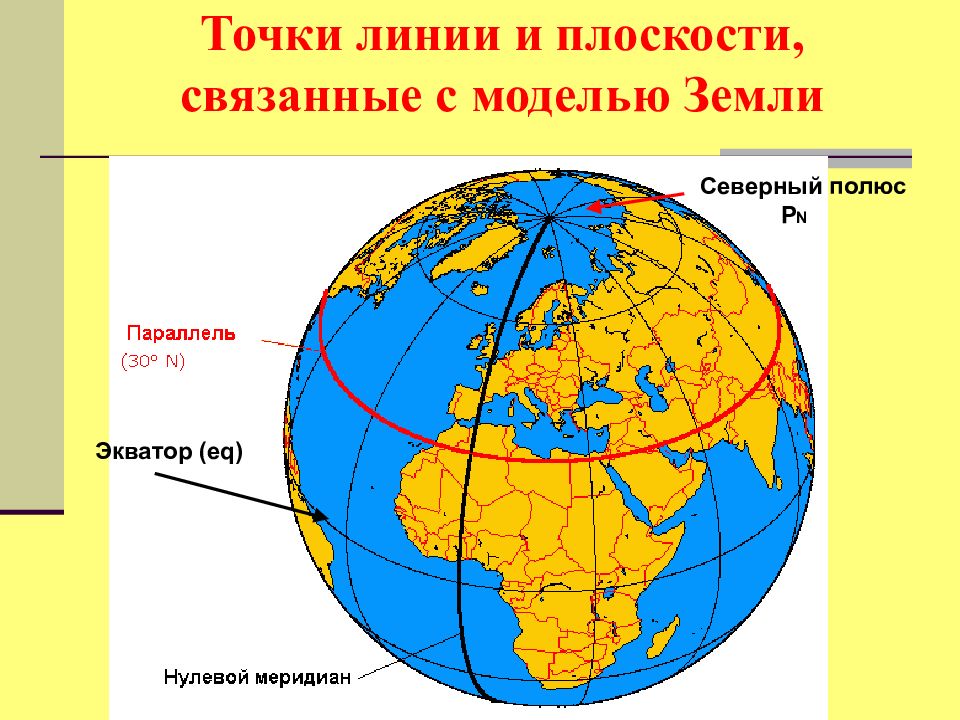
Слайд 13: Точки линии и плоскости, связанные с моделью Земли
Экватор ( eq) Северный полюс Р N
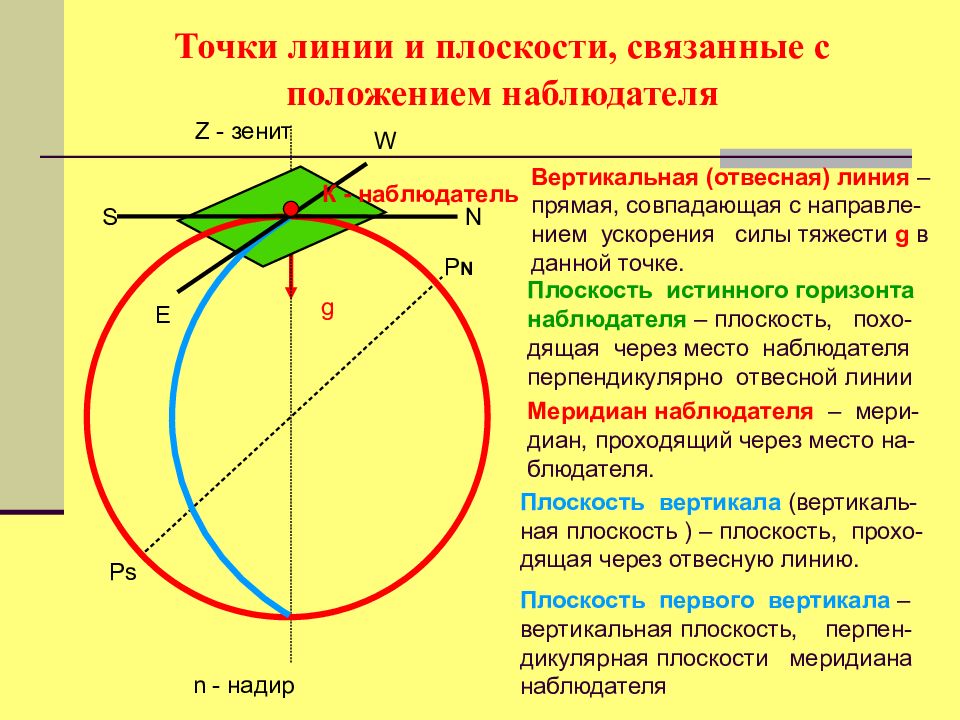
Слайд 14: Точки линии и плоскости, связанные с положением наблюдателя
P N Ps g Вертикальная (отвесная) линия – прямая, совпадающая с направле - нием ускорения силы тяжести g в данной точке. Z - зенит n - надир Плоскость истинного горизонта наблюдателя – плоскость, похо - дящая через место наблюдателя перпендикулярно отвесной линии Меридиан наблюдателя – мери - диан, проходящий через место на - блюдателя. Плоскость вертикала (вертикаль-ная плоскость ) – плоскость, прохо - дящая через отвесную линию. Плоскость первого вертикала – вертикальная плоскость, перпен-дикулярная плоскости меридиана наблюдателя N S E W К - наблюдатель
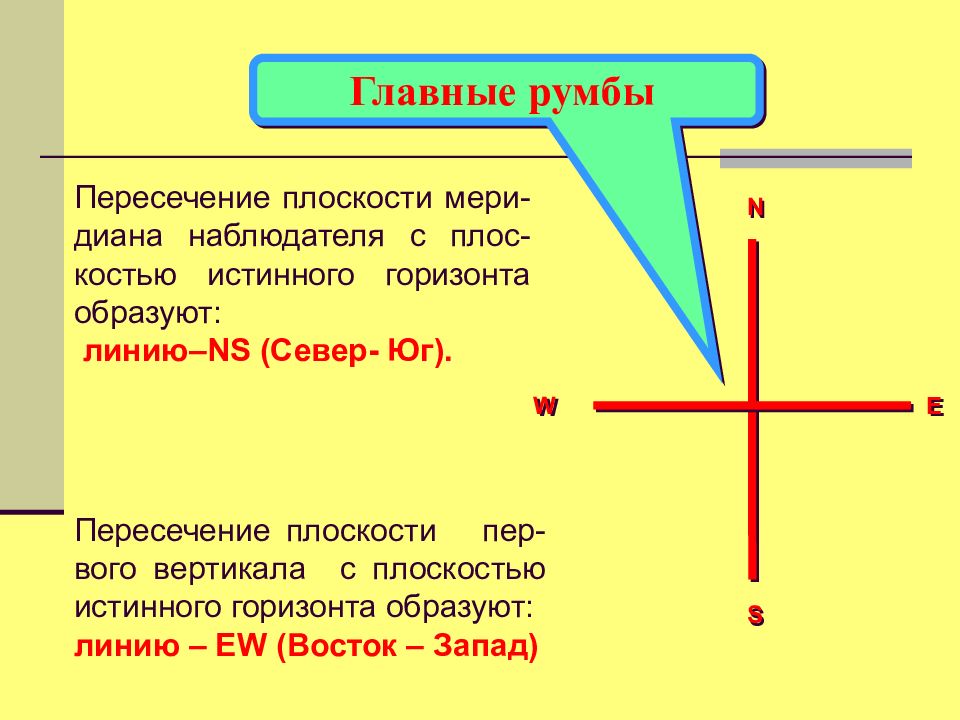
Слайд 15: Главные румбы
Пересечение плоскости пер-вого вертикала с плоскостью истинного горизонта образуют: линию – EW (Восток – Запад ) Пересечение плоскости мери-диана наблюдателя с плос-костью истинного горизонта образуют: линию–NS (Север- Юг). N S E W
Слайд 16
Координаты, применяемые в кораблевождении. географическая; квазигеографическая; прямоугольная; полярная. При решении задач кораблевождения применяются следующие системы координат:
Слайд 17
Географическая система координат Географические координаты : широта и долгота. Координатные оси : экватор и начальный (Гринвичский) меридиан. Координатные линии : меридианы и параллели;
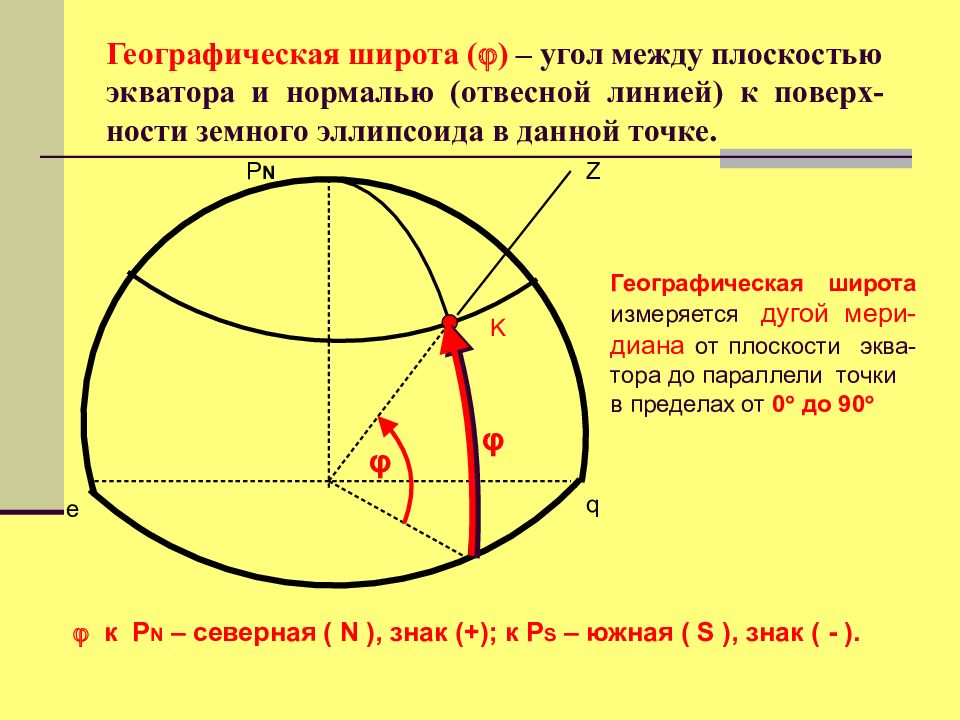
е q P N Z к P N – северная ( N ), знак (+); к P S – южная ( S ), знак ( - ). K φ Географическая широта измеряется дугой мери - диана от плоскости эква - тора до параллели точки в пределах от 0 до 90 φ
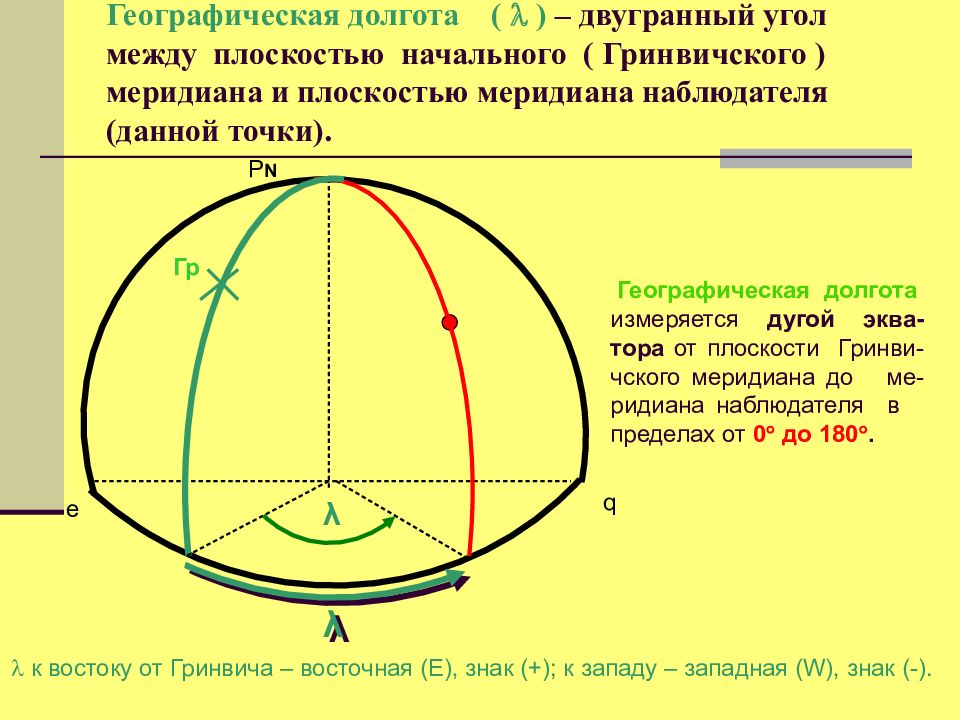
Слайд 19: Географическая долгота ( ) – двугранный угол между плоскостью начального ( Гринвичского ) меридиана и плоскостью меридиана наблюдателя (данной точки)
P N е q Гр Географическая долгота измеряется дугой эква - тора от плоскости Гринви - чского меридиана до ме - ридиана наблюдателя в пределах от 0 до 180. λ к востоку от Гринвича – восточная (Е), знак (+); к западу – западная (W), знак (-). λ
Слайд 20: Географическая система координат
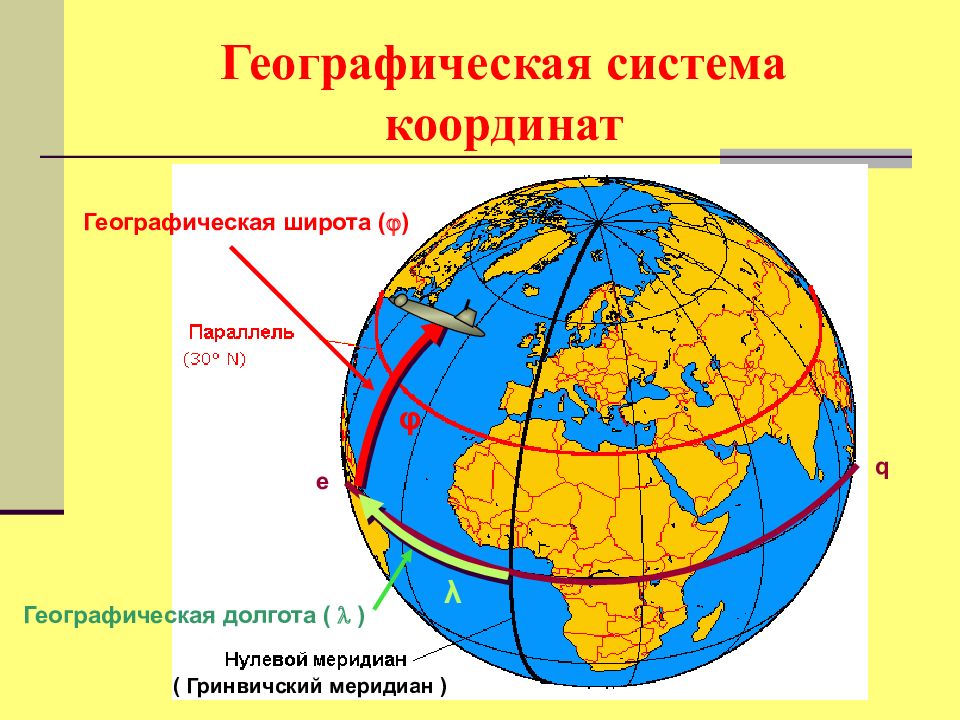
( Гринвичский меридиан ) q e φ λ Географическая широта ( ) Географическая долгота ( )
Слайд 21: Разность широт и долгот
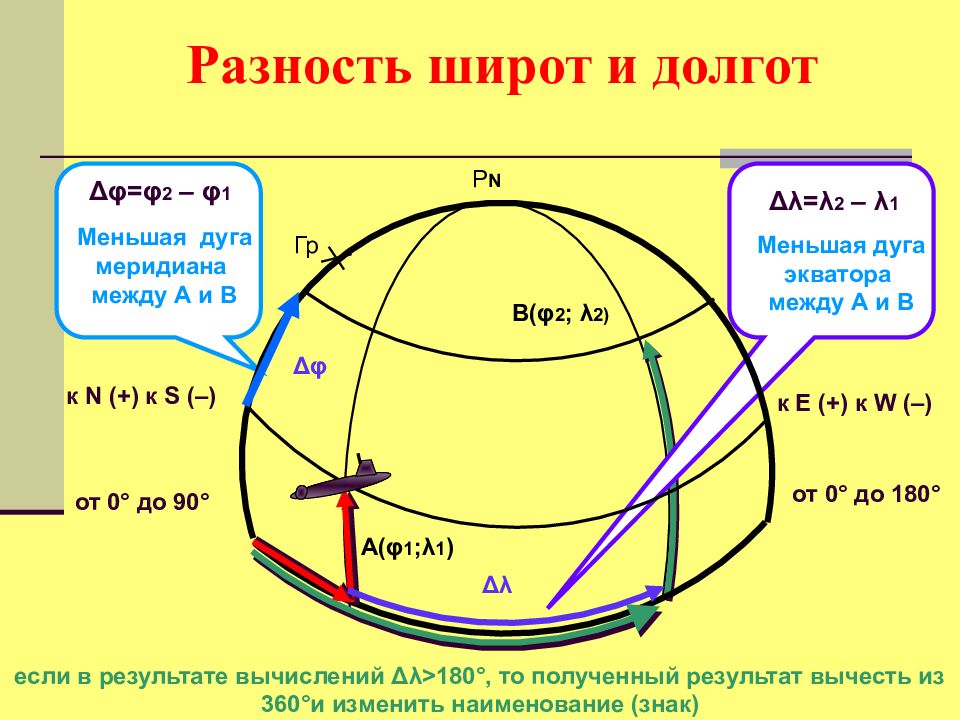
P N Гр А( φ 1 ; λ 1 ) В( φ 2 ; λ 2) Δφ=φ 2 – φ 1 Меньшая дуга меридиана между А и В Δφ Δλ=λ 2 – λ 1 к N (+) к S (–) от 0° до 90° Меньшая дуга экватора между А и В к Е (+) к W (–) от 0° до 180° Δλ если в результате вычислений Δλ>180°, то полученный результат вычесть из 360°и изменить наименование (знак)
Слайд 22
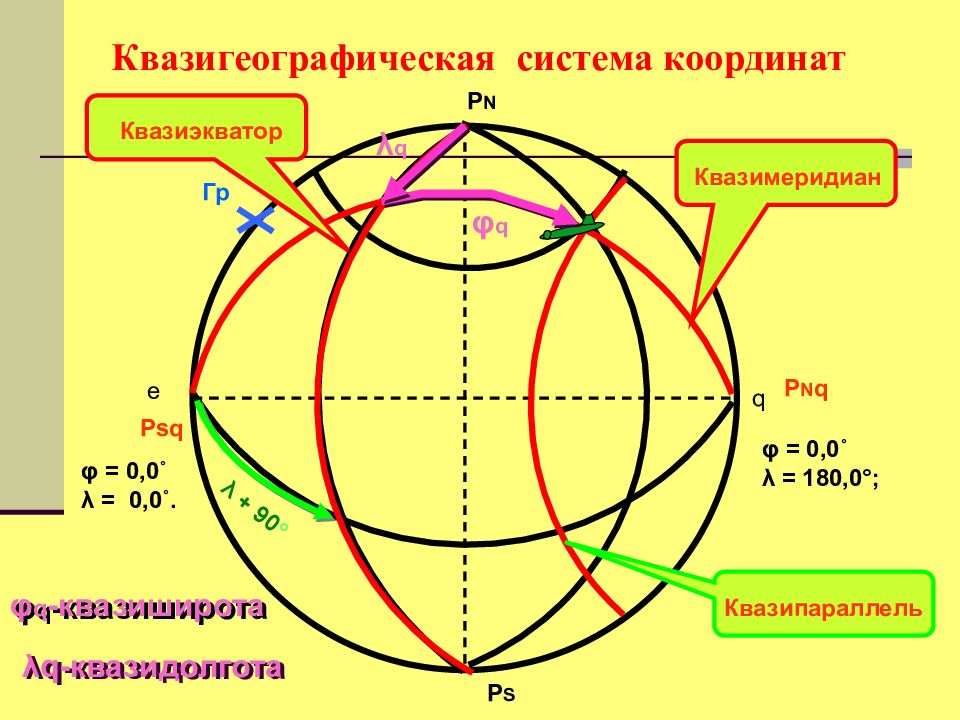
Квазигеографическая система координат (от лат. q uasi – якобы, как будто, приставка, употребляемая в сочетании с некоторыми терминами для определения понятий, которые не являясь в точном значении слова этими терминами, тем не менее заменяют их ) - условная система координат используемая для кораблевождения в высоких широтах (более 80 град.) – приполюсных районах Северного Ледовитого океана. Квазигеографические полюса, смещены относительно географи - ческих, на угол 90˚ и имеют следующие координаты: Северный квазиполюс ( Pnq ) φ = 0,0˚ λ = 180,0; Южный квазиполюс ( Psq ) φ = 0,0˚ λ = 0,0˚. Координатные линии системы - квазипараллели и квазимеридианы, а координаты - квазиширота (φ q ) и квазидолгота (λ q ). Квазигеографическая система координат
Слайд 23: Квазигеографическая система координат
P N P S e q Гр Psq φ = 0,0˚ λ = 0,0˚. φ = 0,0˚ λ = 180,0 ° ; P N q Квазимеридиан λ + 90 ° Квазиэкватор Квазипараллель φ q λ q λ q -квазидолгота φ q - квазиширота
Слайд 24
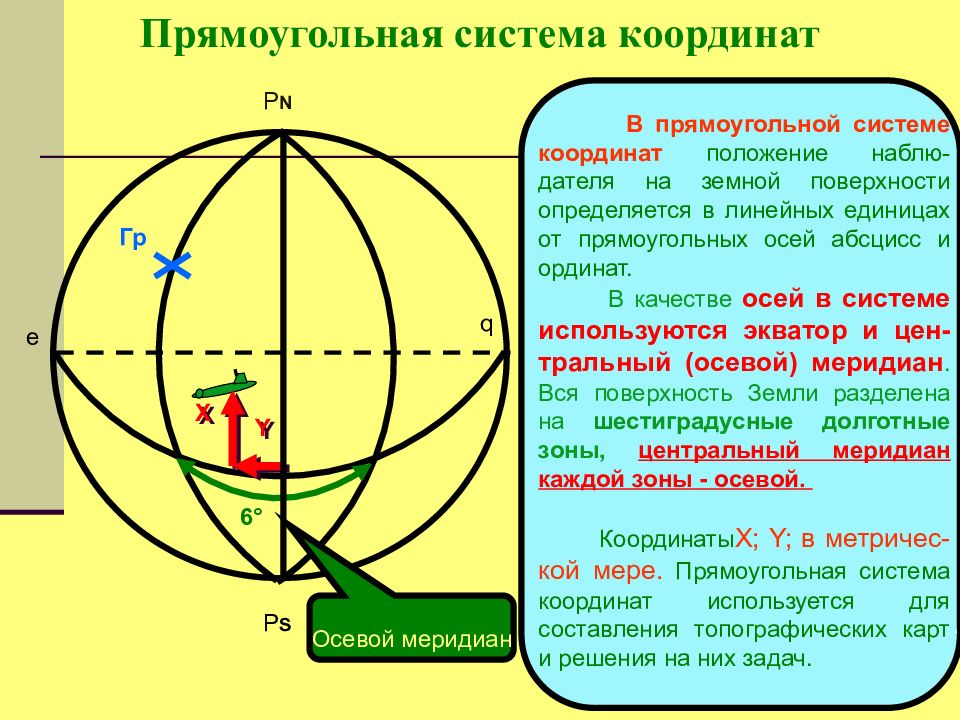
Прямоугольная система координат В прямоугольной системе координат положение наблю-дателя на земной поверхности определяется в линейных единицах от прямоугольных осей абсцисс и ординат. В качестве осей в системе используются экватор и цен - тральный (осевой) меридиан. Вся поверхность Земли разделена на шестиградусные долготные зоны, центральный меридиан каждой зоны - осевой. Координаты X; Y; в метричес - кой мере. Прямоугольная система координат используется для составления топографических карт и решения на них задач. 6 ° Х Y Гр P N P S Осевой меридиан e q
Слайд 25
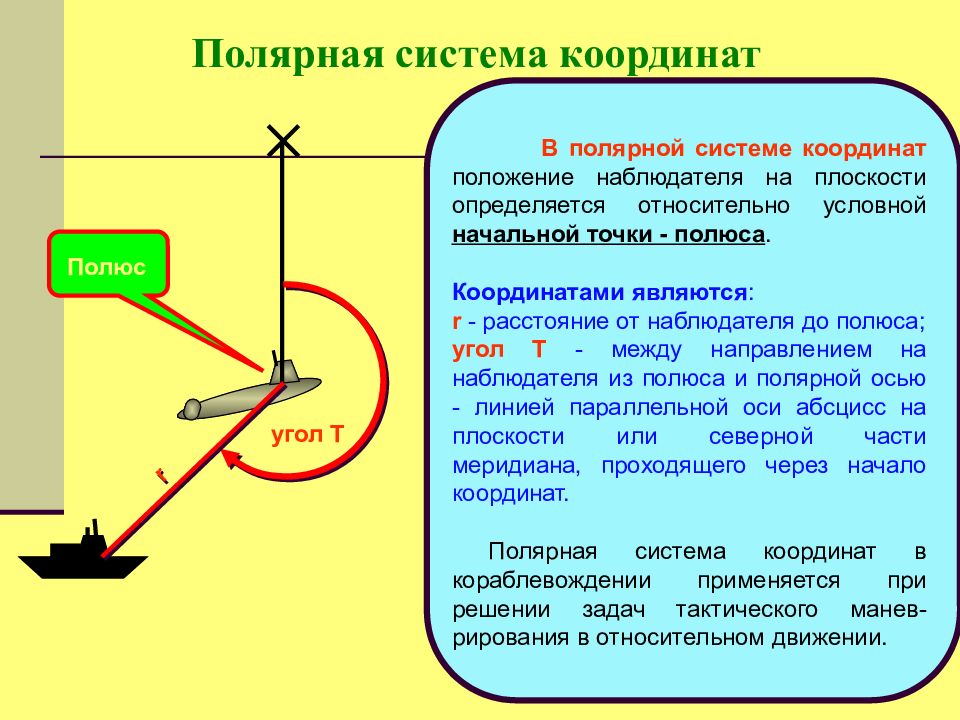
В полярной системе координат положение наблюдателя на плоскости определяется относительно условной начальной точки - полюса. Координатами являются : r - расстояние от наблюдателя до полюса; угол Т - между направлением на наблюдателя из полюса и полярной осью - линией параллельной оси абсцисс на плоскости или северной части меридиана, проходящего через начало координат. Полярная система координат в кораблевождении применяется при решении задач тактического манев-рирования в относительном движении. Полярная система координат Полюс угол Т r
Слайд 26: Понятие о радиусах кривизны и длинах дуг земного эллипсоида
Z Р N r a e q Движение корабля по земной поверхности – перемещение по дуге. Чтобы вычислить длину дуги, необходимо знать ее радиус. Сечения эллипсоида плоскостями образуют либо окружности, либо эллипсы. Сечение эллипсоида плоскос - тью, параллельной плоскости эк - ватора, образует окружность – параллель радиуса r. Сечение эллипсоида плоскостью меридиана образует эллипс с радиу - сом кривизны М. Сечение эллипсоида плоскостью первого вертикала ( нормальное сечение) образует эллипс с радиусом кривизны N. M N Ps
Слайд 27
Понятие о радиусах кривизны и длинах дуг земного эллипсоида. Зная радиусы кривизны, можно вычислить длины дуг: длина одной минуты дуги меридиана: 1 м = М · arc 1'; длина одной минуты дуги параллели: 1 ' r = r · arc 1'; длина одной минуты дуги экватора: 1 ' r = а · arc 1'; Примечание: 1 рад.=57,3 =3437,75 ´; arc 1´= 1 / 3437,75´.
Слайд 28
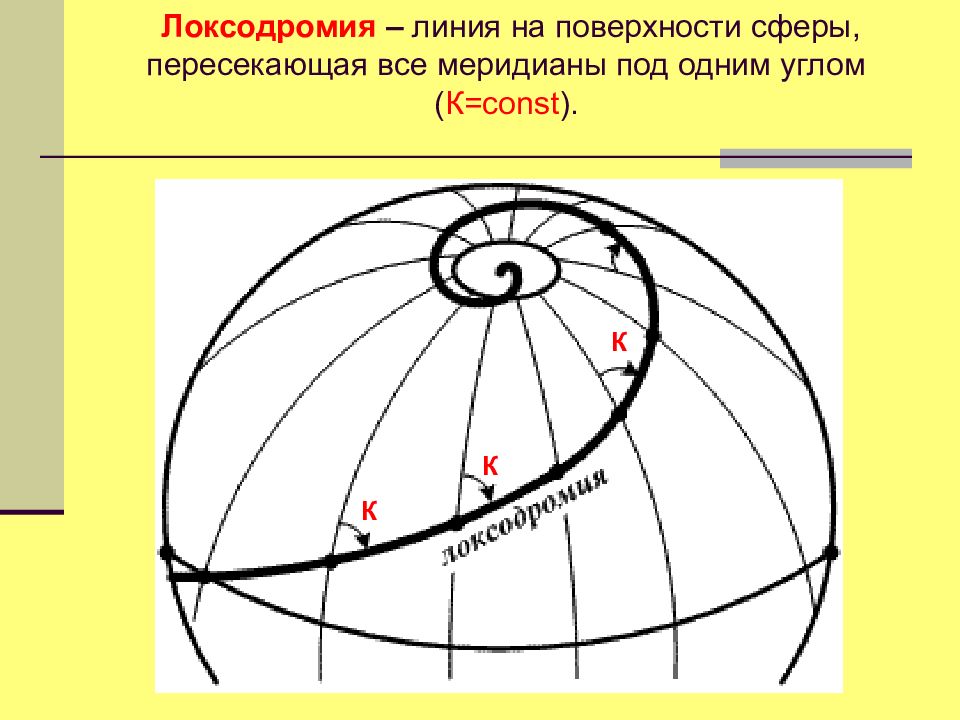
Локсодромия – линия на поверхности сферы, пересекающая все меридианы под одним углом ( К= const ). К К К
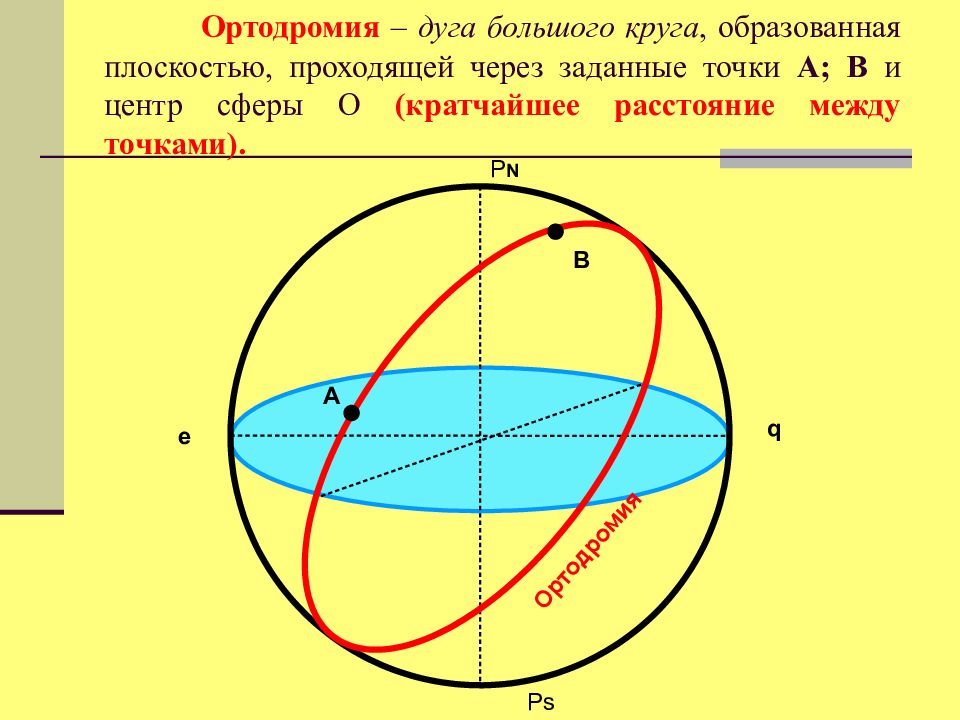
Слайд 29: Ортодромия – дуга большого круга, образованная плоскостью, проходящей через заданные точки А; В и центр сферы О ( кратчайшее расстояние между точками)
Р N Ps e q Ортодромия A B
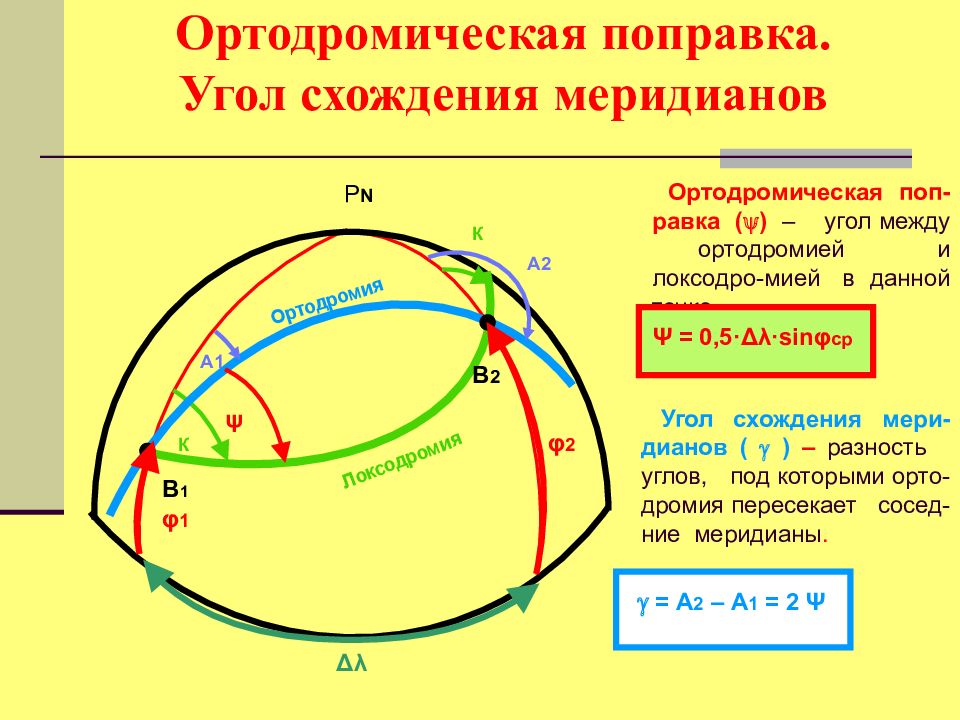
Слайд 30: Ортодромическая поправка. Угол схождения меридианов
Р N Локсодромия К К Ортодромия А1 А2 В 1 В 2 φ 1 φ 2 Δλ ψ Ортодромическая поп-равка ( ) – угол между ортодромией и локсодро-мией в данной точке. Ψ = 0,5 · Δλ ·sin φ ср Угол схождения мери-дианов ( ) – разность углов, под которыми орто-дромия пересекает сосед-ние меридианы. = А 2 – А 1 = 2 Ψ
Слайд 31: Системы счета направлений в навигации
Корабельную –отсчет произво - дится от диамет-ральной плоско-сти (продольной оси) корабля. В зависимости от плоскости (линии), от которой производится отсчет направлений системы счета подразделяются на: Меридианную (географическую) – отсчет произво-дится от меридиа - на наблюдателя;
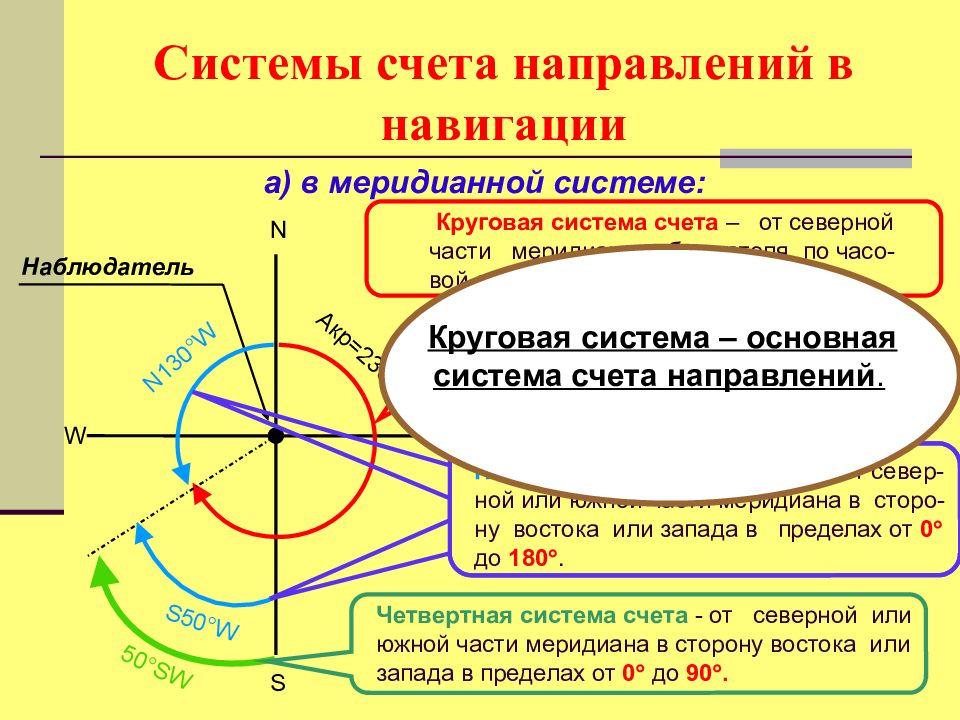
Слайд 32: Системы счета направлений в навигации
N S W E а) в меридианной системе: Наблюдатель Акр=230 ° Круговая система счета – от северной части меридиана наблюдателя, по часо - вой стрелке от 0 до 360 . N130 °W S50 °W Полукруговая система счета – от север-ной или южной части меридиана в сторо-ну востока или запада в пределах от 0 до 180 . 50 °SW Четвертная система счета - от северной или южной части меридиана в сторону востока или запада в пределах от 0 до 90 . Круговая система – основная система счета направлений.
Слайд 33: б) в корабельной системе:
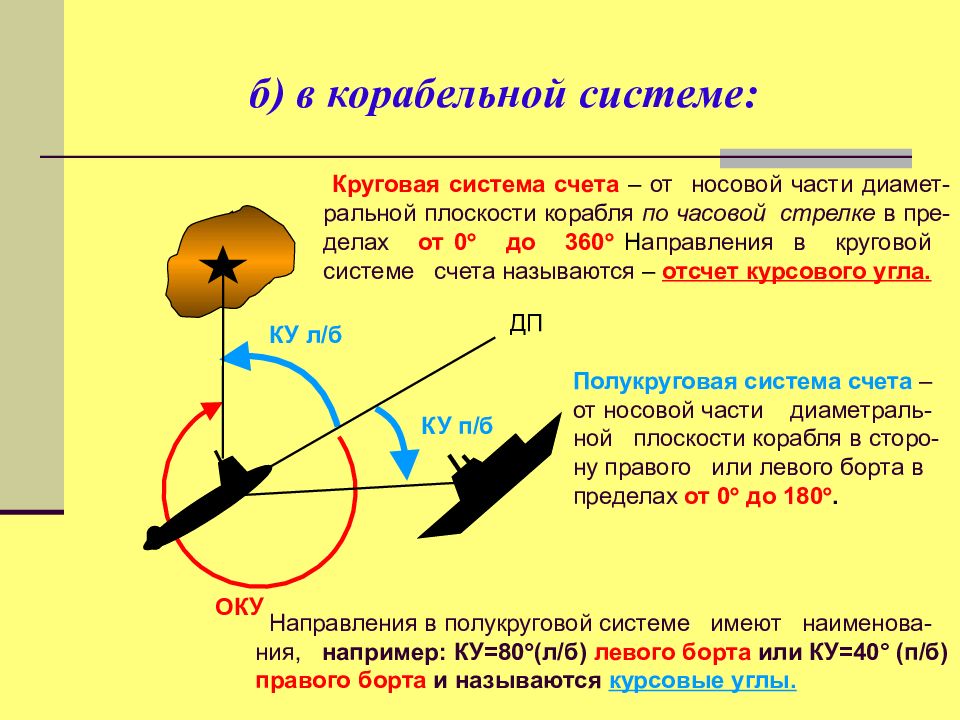
ОКУ Круговая система счета – от носовой части диамет-ральной плоскости корабля по часовой стрелке в пре-делах от 0 до 360 Н аправления в круговой системе счета называются – отсчет курсового угла. КУ п/б КУ л/б Направления в полукруговой системе имеют наименова-ния, например: КУ=80 (л/б) левого борта или КУ=40° (п/б) правого борта и называются курсовые углы. Полукруговая система счета – от носовой части диаметраль-ной плоскости корабля в сторо-ну правого или левого борта в пределах от 0 до 180 . ДП
Слайд 34: Для определения направления движения пл и направлений на другие объекты в меридианной системе введены понятия: курс и пеленг
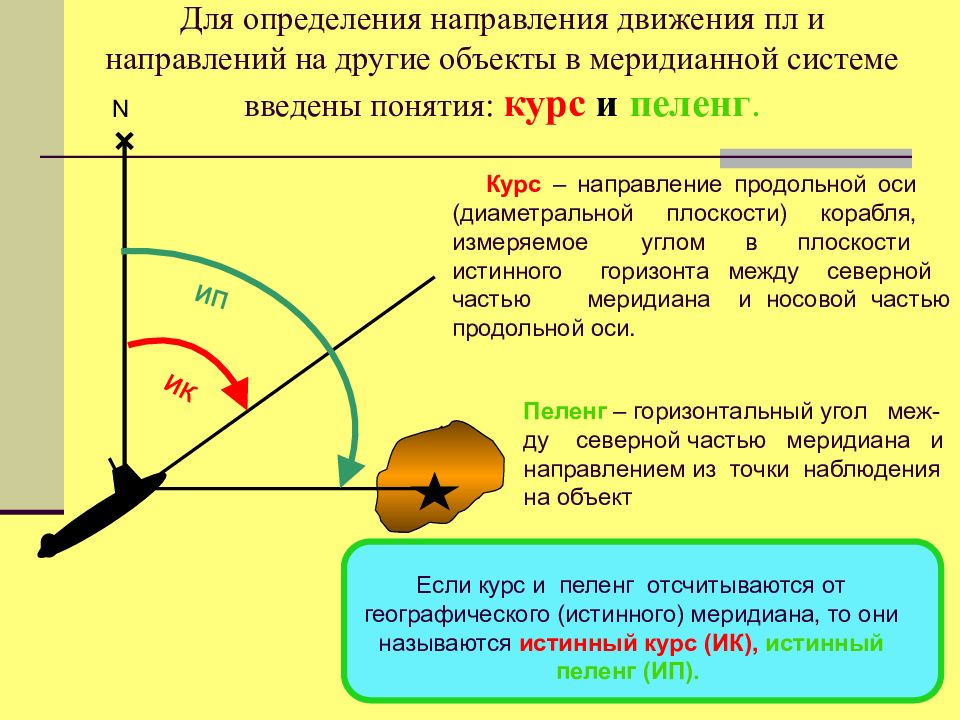
N Курс – направление продольной оси (диаметральной плоскости) корабля, измеряемое углом в плоскости истинного горизонта между северной частью меридиана и носовой частью продольной оси. ИК Пеленг – горизонтальный угол меж-ду северной частью меридиана и направлением из точки наблюдения на объект ИП Если курс и пеленг отсчитываются от географического (истинного) меридиана, то они называются истинный курс (ИК), истинный пеленг (ИП).
Слайд 35: Связь между меридианной и корабельной системами счета
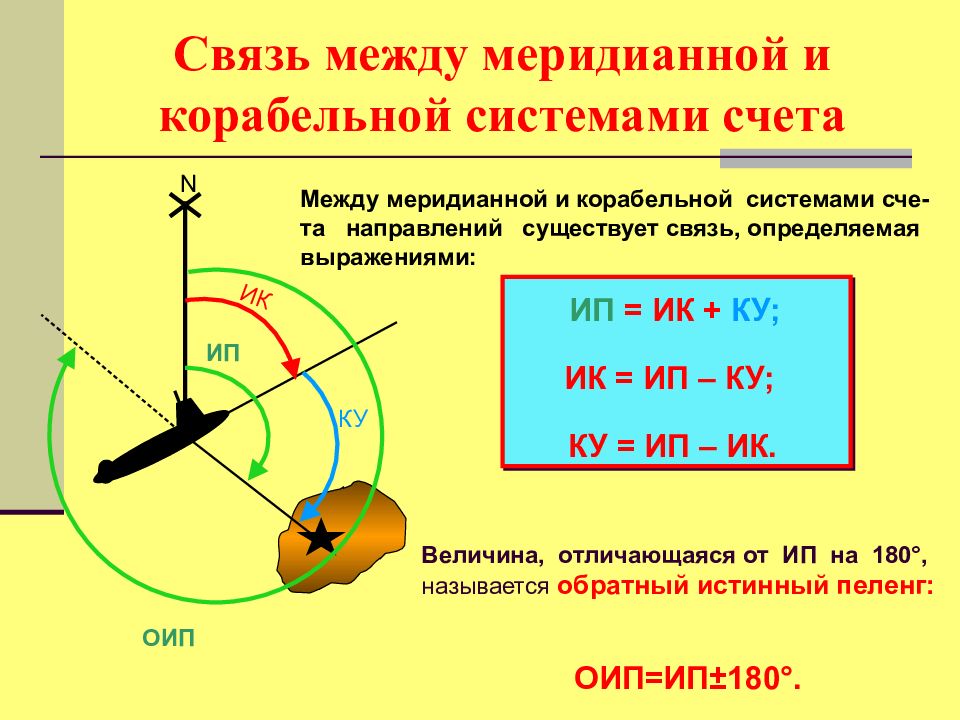
N Между меридианной и корабельной системами сче-та направлений существует связь, определяемая выражениями: ИК КУ ИП ИП = ИК + КУ; ИК = ИП – КУ; КУ = ИП – ИК. Величина, отличающаяся от ИП на 180°, называется обратный истинный пеленг: ОИП=ИП±180°. ОИП
Слайд 36: Компасные направления
Корабельная система курсоуказания (курсоуказатели ). Внешний вид гирокомпаса «Курс–3» и его чувствительного элемента. Для выработки и хранения направления меридиана на корабле предназначена:
Слайд 37: Компасные направления
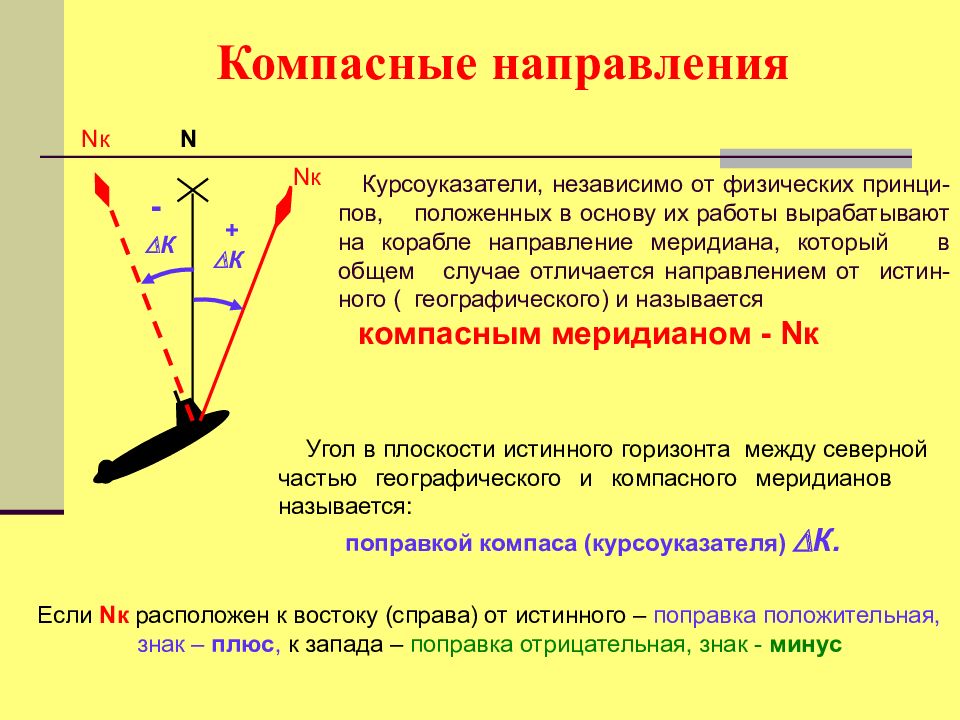
Курсоуказатели, независимо от физических принци - пов, положенных в основу их работы вырабатывают на корабле направление меридиана, который в общем случае отличается направлением от истин - ного ( географического) и называется компасным меридианом - N к N N к Угол в плоскости истинного горизонта между северной частью географического и компасного меридианов называется: поправкой компаса (курсоуказателя) К. Если N к расположен к востоку (справа) от истинного – поправка положительная, знак – плюс, к запада – поправка отрицательная, знак - минус К + N к К -
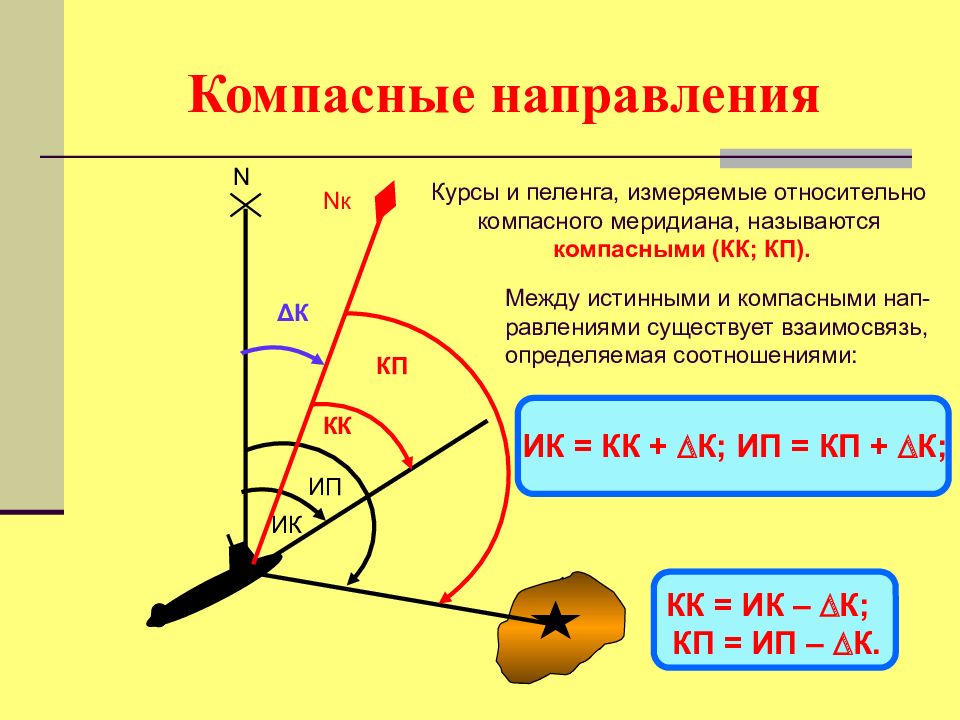
Слайд 38: Компасные направления
Курсы и пеленга, измеряемые относительно компасного меридиана, называются компасными (КК; КП). N ИК ИП N к КК КП Δ К Между истинными и компасными нап-равлениями существует взаимосвязь, определяемая соотношениями: ИК = КК + К; ИП = КП + К; КК = ИК – К; КП = ИП – К.
Слайд 39: Определение поправки компаса
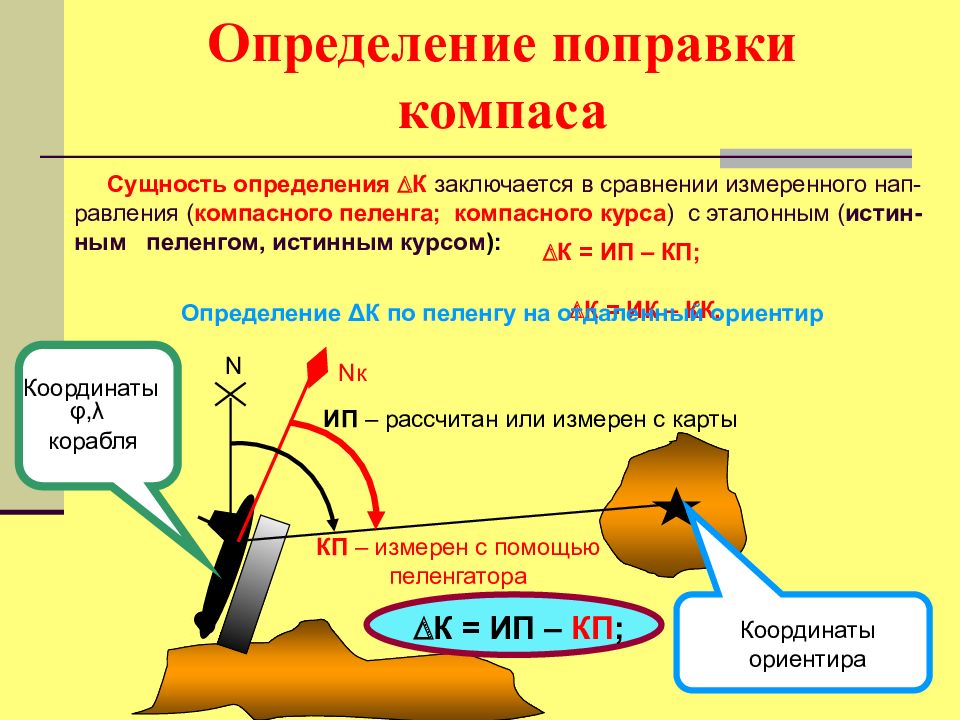
Сущность определения К заключается в сравнении измеренного нап - равления ( компасного пеленга; компасного курса ) с эталонным ( истин - ным пеленгом, истинным курсом ): К = ИП – КП; К = ИК – КК. Определение Δ К по пеленгу на отдаленный ориентир N N к Координаты φ, λ корабля Координаты ориентира ИП – рассчитан или измерен с карты КП – измерен с помощью пеленгатора К = ИП – КП ;
Слайд 40: Расчет направлений по магнитному компасу
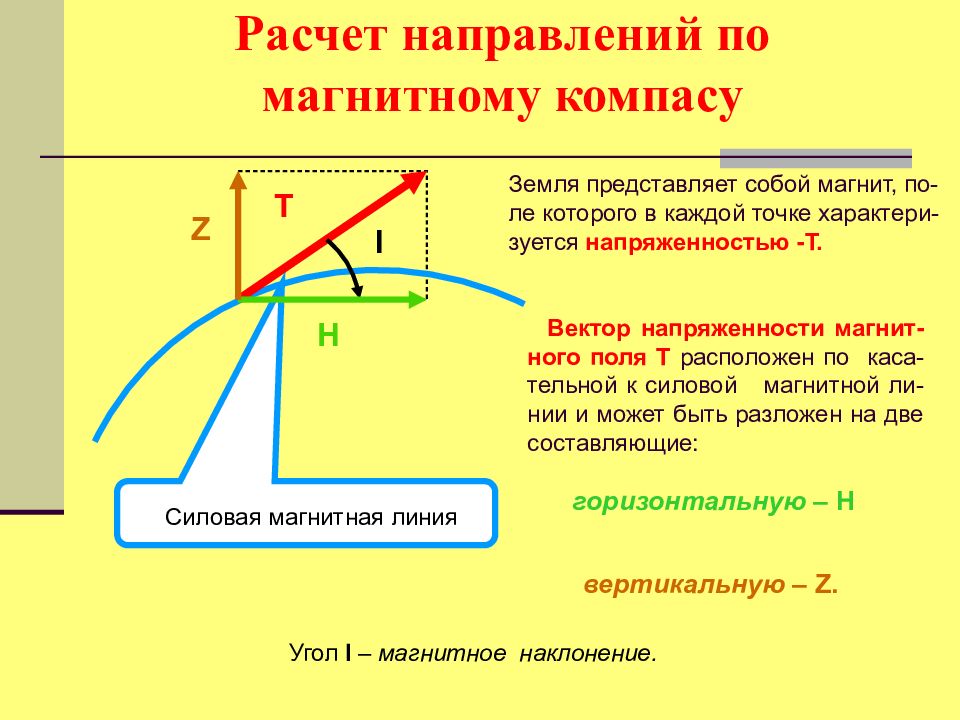
Т Расчет направлений по магнитному компасу Силовая магнитная линия Земля представляет собой магнит, по-ле которого в каждой точке характери-зуется напряженностью -T. Вектор напряженности магнит-ного поля Т расположен по каса-тельной к силовой магнитной ли-нии и может быть разложен на две составляющие: горизонтальную – H вертикальную – Z. I Угол I – магнитное наклонение. Н Z
Слайд 42: Расчет направлений по магнитному компасу
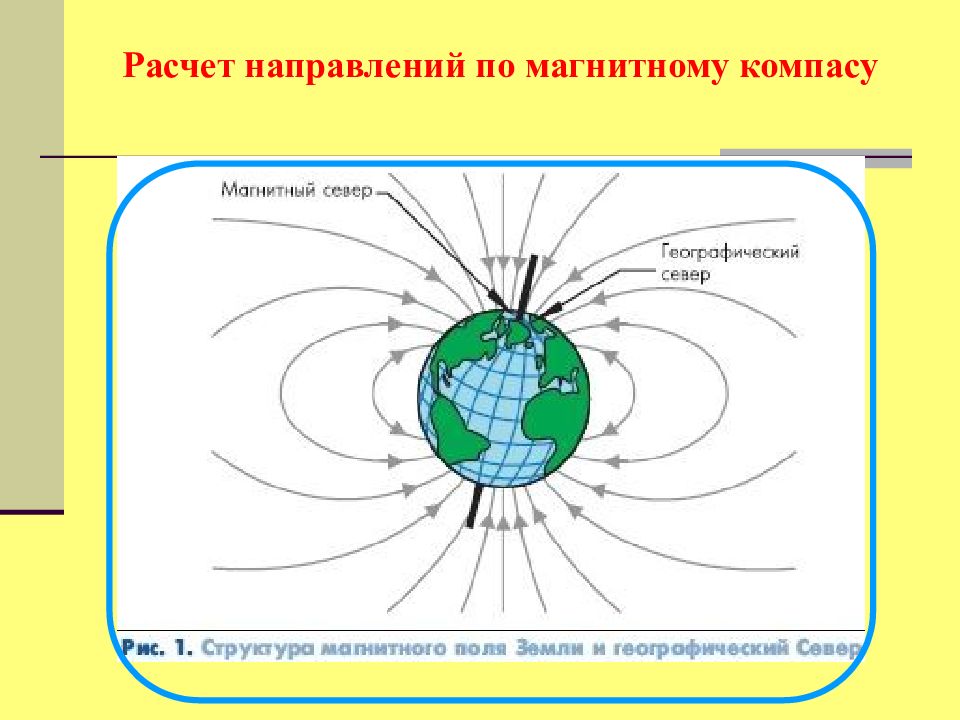
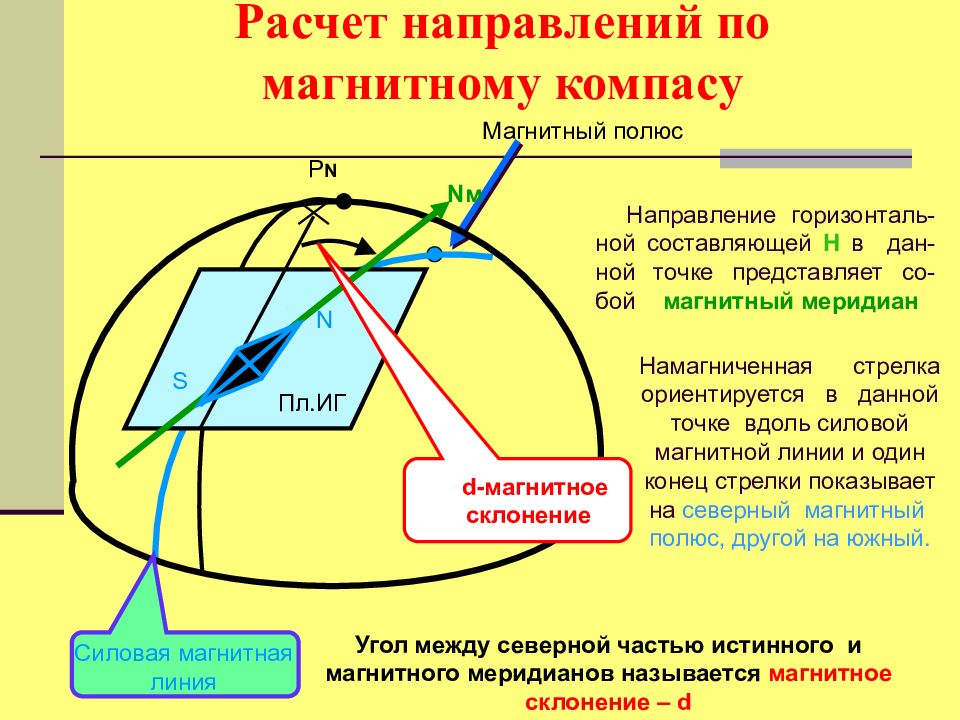
Магнитный полюс Пл.ИГ Расчет направлений по магнитному компасу P N Силовая магнитная линия N м N S d -магнитное склонение Направление горизонталь-ной составляющей Н в дан-ной точке представляет со-бой магнитный меридиан Намагниченная стрелка ориентируется в данной точке вдоль силовой магнитной линии и один конец стрелки показывает на северный магнитный полюс, другой на южный. Угол между северной частью истинного и магнитного меридианов называется магнитное склонение – d
Слайд 43: Магнитные направления
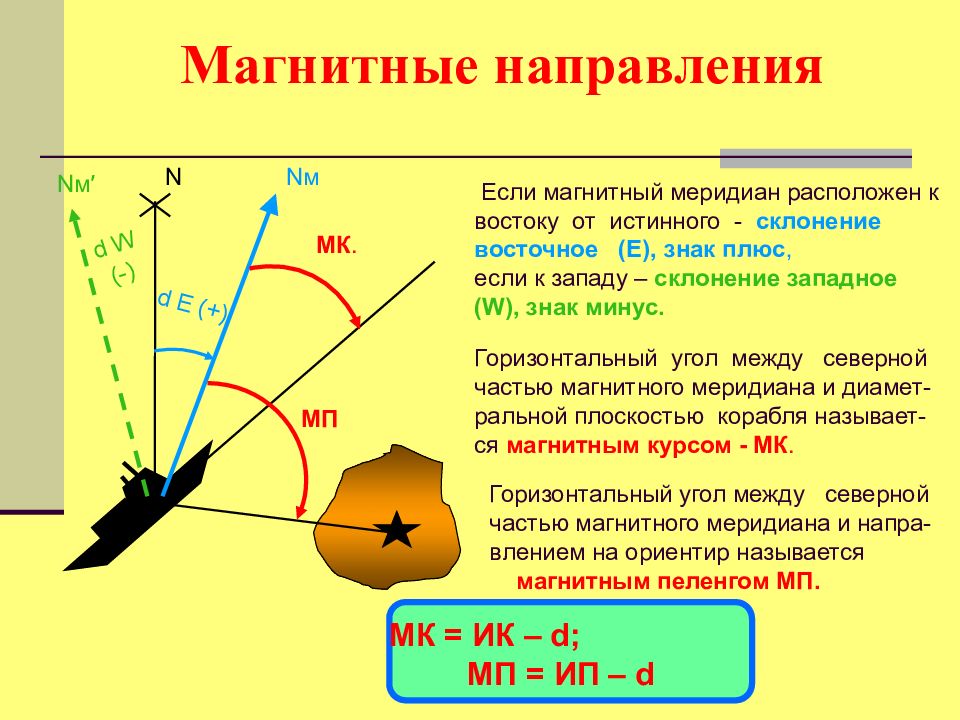
N N м Если магнитный меридиан расположен к востоку от истинного - склонение восточное (Е), знак плюс, если к западу – склонение западное (W), знак минус. d Е (+) N м ′ d W (-) Горизонтальный угол между северной частью магнитного меридиана и диамет - ральной плоскостью корабля называет - ся магнитным курсом - МК. МК. Горизонтальный угол между северной частью магнитного меридиана и напра - влением на ориентир называется магнитным пеленгом МП. МП МК = ИК – d ; МП = ИП – d
Слайд 44: Приведение магнитного склонения к году плавания
d = d к + Δ d · n dk - магнитное склонение с карты Δ d - годовое изменение с карты n - количество лет между годом издания МНК и годом плавания
Слайд 45: Девиация магнитного компаса
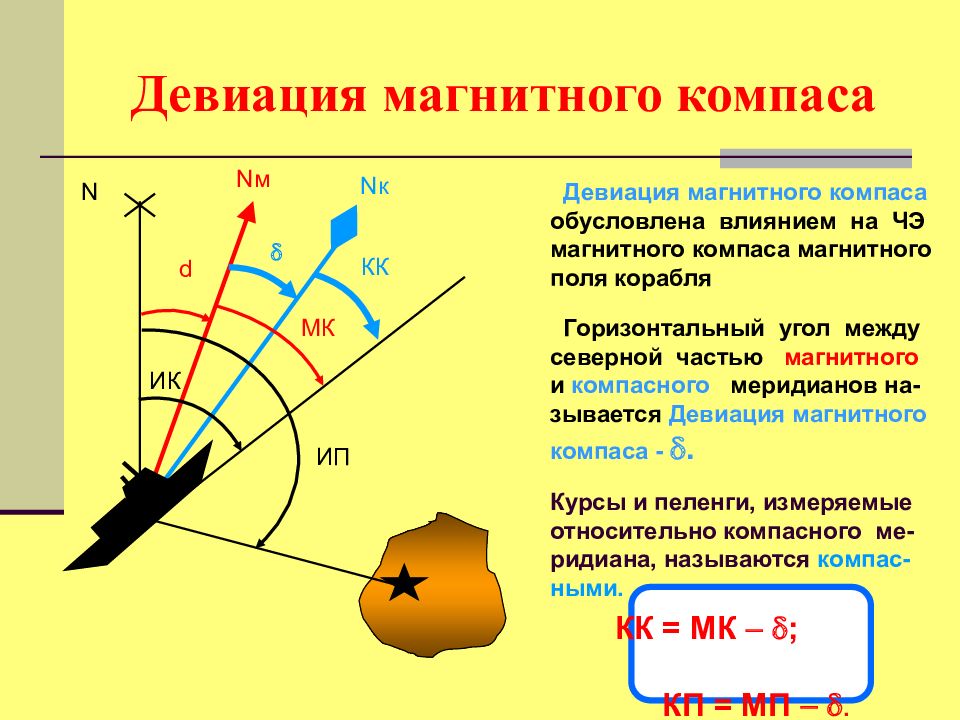
Девиация магнитного компаса обусловлена влиянием на ЧЭ магнитного компаса магнитного поля корабля N м d Горизонтальный угол между северной частью магнитного и компасного меридианов на- зывается Девиация магнитного компаса - . N к N ИК ИП МК КК Курсы и пеленги, измеряемые относительно компасного ме-ридиана, называются компас-ными. КК = МК ; КП = МП .
Слайд 46: Поправка магнитного компаса
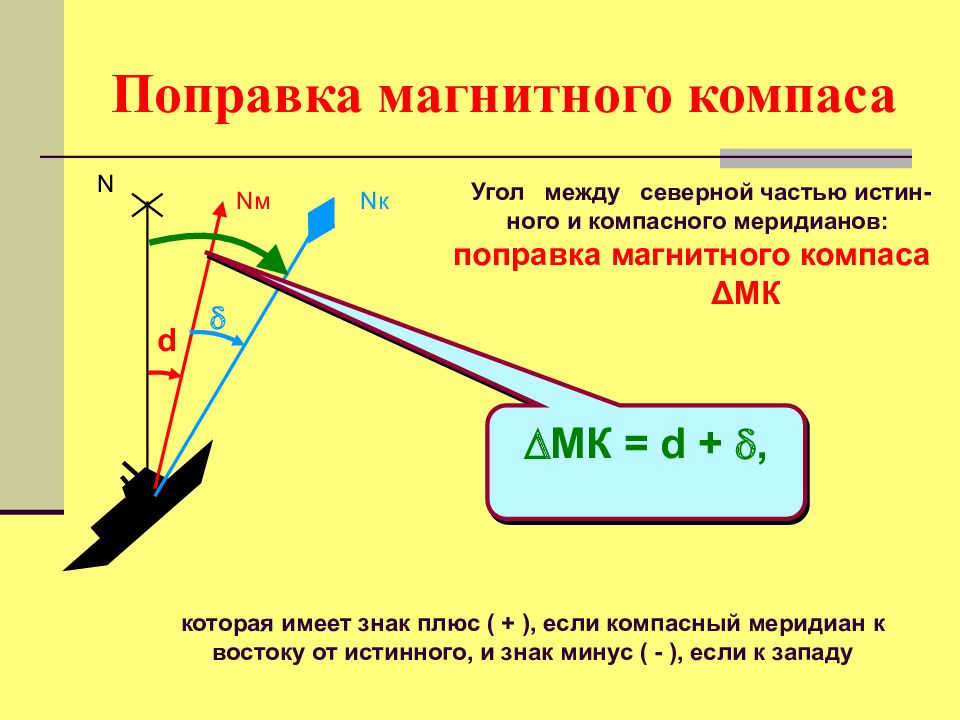
Угол между северной частью истин - ного и компасного меридианов: поправка магнитного компаса Δ МК N N м d N к МК = d + , которая имеет знак плюс ( + ), если компасный меридиан к востоку от истинного, и знак минус ( - ), если к западу
Слайд 48: Скорость корабля
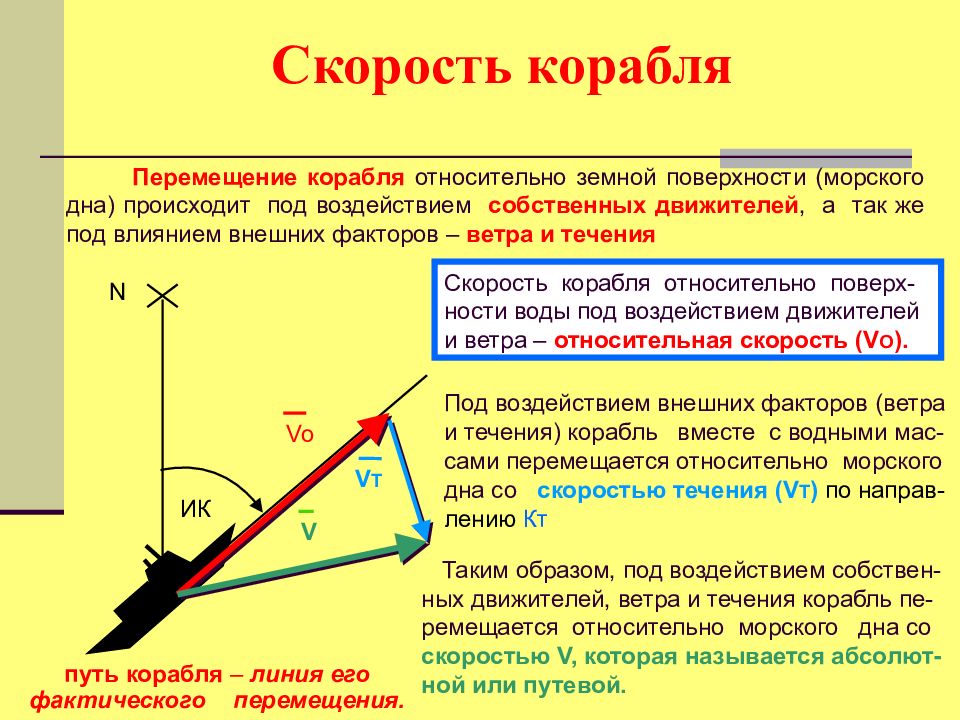
Перемещение корабля относительно земной поверхности (морского дна) происходит под воздействием собственных движителей, а так же под влиянием внешних факторов – ветра и течения N ИК Скорость корабля относительно поверх-ности воды под воздействием движителей и ветра – относительная скорость (V O ). Vo Под воздействием внешних факторов (ветра и течения) корабль вместе с водными мас-сами перемещается относительно морского дна со скоростью течения ( V Т ) по направ-лению Кт V Т Таким образом, под воздействием собствен-ных движителей, ветра и течения корабль пе-ремещается относительно морского дна со скоростью V, которая называется абсолют-ной или путевой. V путь корабля – линия его фактического перемещения.
Слайд 49: Единицы длины и скорости в навигации
1 м = М · arc 1 = 1852,3 – 9,3 · cos 2 М – радиус кривизны меридиана эллипсоида. Единицы длины и скорости в навигации Основной единицей длины в навигации является морская миля. Морская миля – длина одной минуты дуги меридиана эллипсоида В 1931 году в качестве единицы длины была принята стандартная миля, равная длине одной минуты дуги меридиана эллипсоида в ши - роте 44 18 и составляющая 1852 метра. В настоящее время термин стандартная миля практически вы - шел из употребления и заменен термином – морская миля. Кабельтов – одна десятая часть морской мили = 185,2 метра
Слайд 50: Единицы длины и скорости в навигации
Основной единицей скорости в навигации явля-ется узел – скорость, равная одной морской миле в час. При решении некоторых задач кораблевождения приме-няется единица скорости – кабельтов в минуту. Для перехода от скорости в узлах к скорости в каб/мин используется соотношение: Скорость в узлах : 6 = скорость в каб/мин.
Слайд 51: Измерители скорости на корабле
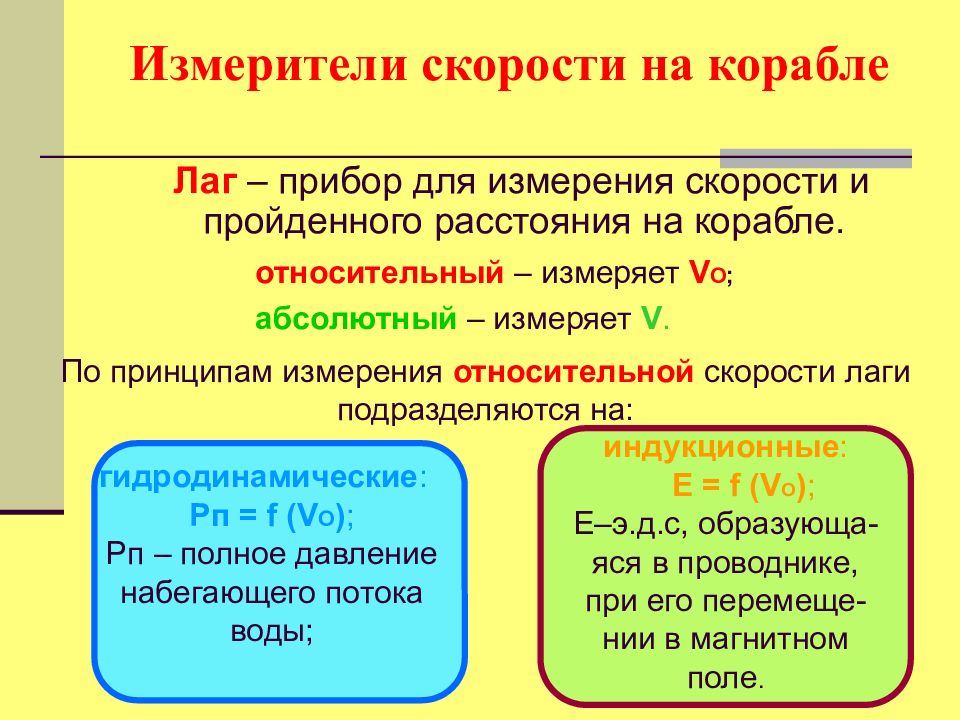
Лаг – прибор для измерения скорости и пройденного расстояния на корабле. относительный – измеряет V O ; абсолютный – измеряет V. По принципам измерения относительной скорости лаги подразделяются на: гидродинамические : Рп = f (V O ) ; Рп – полное давление набегающего потока воды; индукционные : Е = f (V O ) ; Е–э.д.с, образующа-яся в проводнике, при его перемеще-нии в магнитном поле.
Слайд 52: Измерители скорости на корабле
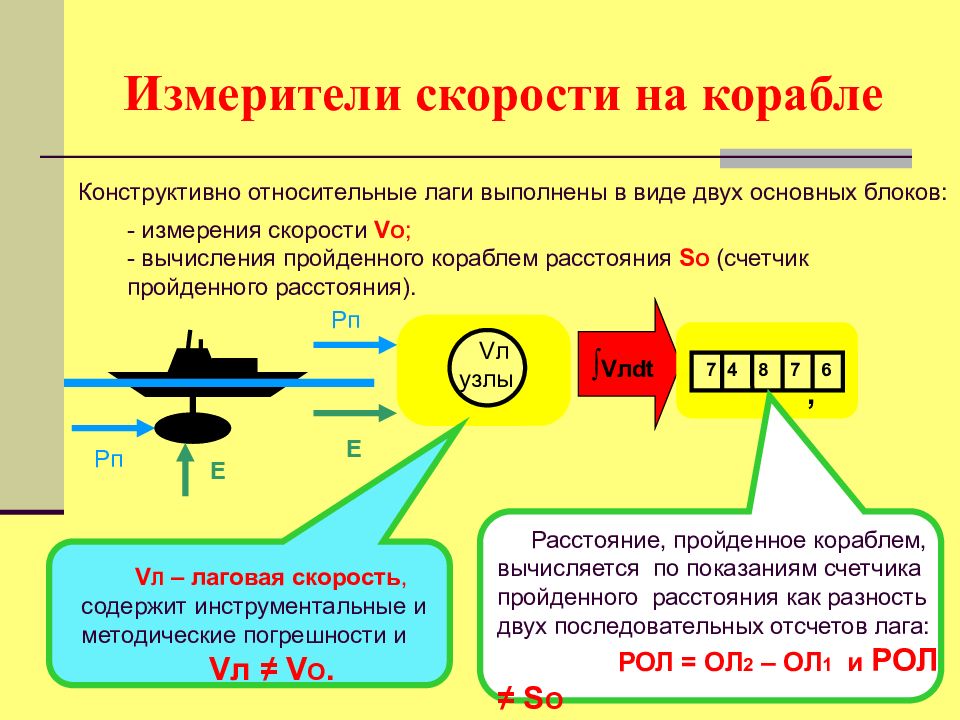
Конструктивно относительные лаги выполнены в виде двух основных блоков: - измерения скорости V O ; - вычисления пройденного кораблем расстояния S O (счетчик пройденного расстояния). V л узлы Е Е Рп Рп ∫ V л dt 7 4 8 7 6 ‚ V Л – лаговая скорость, содержит инструментальные и методические погрешности и V л ≠ V O. Расстояние, пройденное кораблем, вычисляется по показаниям счетчика пройденного расстояния как разность двух последовательных отсчетов лага: РОЛ = ОЛ 2 – ОЛ 1 и РОЛ ≠ S O
Слайд 53: Понятие об определении поправок относительного лага
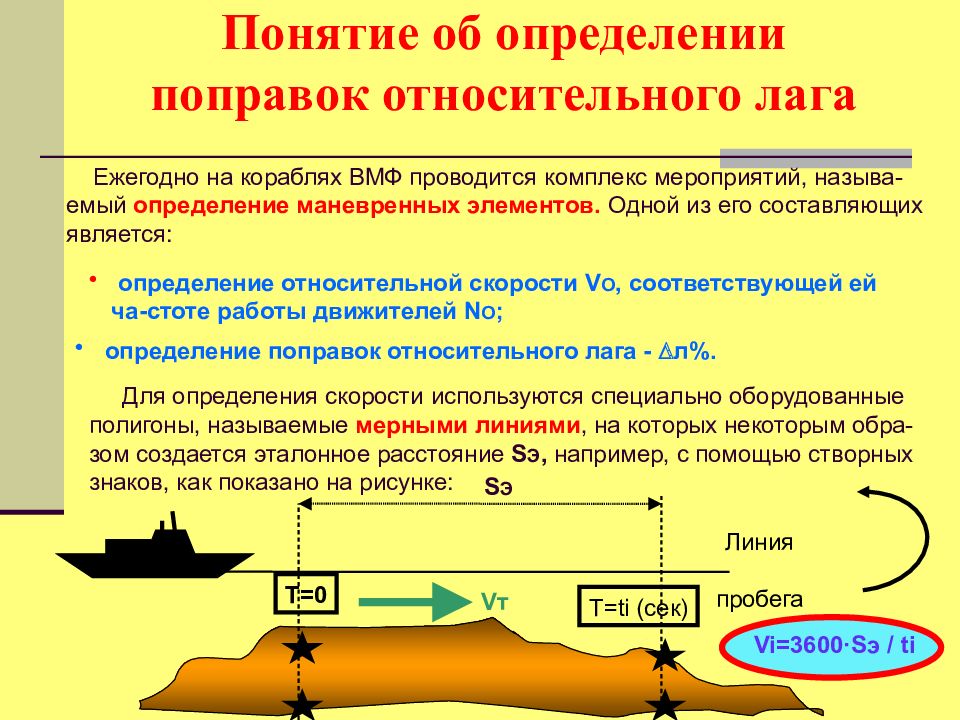
Линия пробега Понятие об определении поправок относительного лага Ежегодно на кораблях ВМФ проводится комплекс мероприятий, называ-емый определение маневренных элементов. Одной из его составляющих является: определение относительной скорости V O, соответствующей ей ча-стоте работы движителей N O ; определение поправок относительного лага - л%. Для определения скорости используются специально оборудованные полигоны, называемые мерными линиями, на которых некоторым обра-зом создается эталонное расстояние S Э, например, с помощью створных знаков, как показано на рисунке: S Э Т=0 Т= ti ( сек) Vi=3600 ·S э / ti V т
Слайд 54: Понятие об определении поправок относительного лага
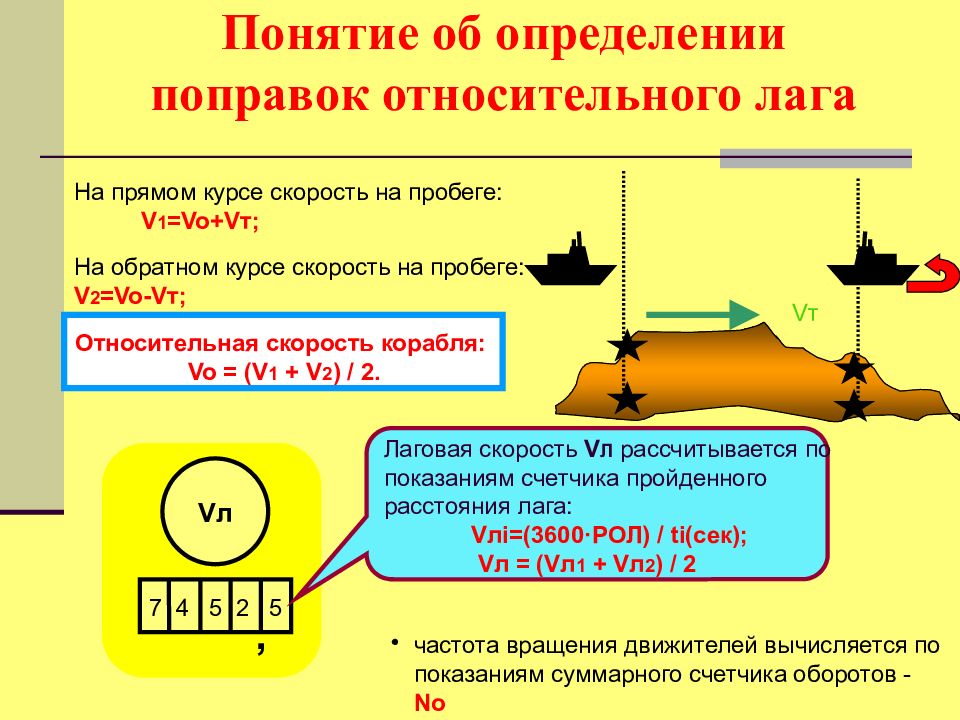
V л 7 4 5 2 5 , Понятие об определении поправок относительного лага На прямом курсе скорость на пробеге: V 1 =Vo+V т; V т Относительная скорость корабля: Vo = (V 1 + V 2 ) / 2. На обратном курсе скорость на пробеге: V 2 =Vo - V т; Лаговая скорость V Л рассчитывается по показаниям счетчика пройденного расстояния лага: V л i =(3600 · РОЛ) / ti (сек); V л = (V л 1 + V л 2 ) / 2 частота вращения движителей вычисляется по показаниям суммарного счетчика оборотов - No
Слайд 55: Понятие об определении поправок относительного лага
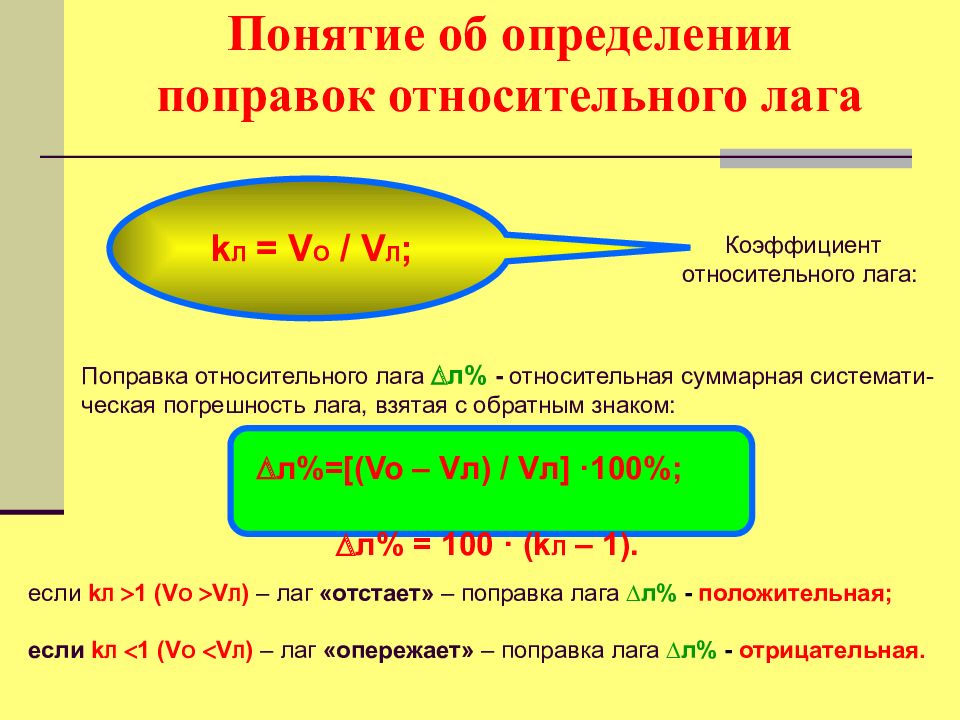
если k Л 1 (V O V Л ) – лаг «отстает» – поправка лага л% - положительная; если k Л 1 (V O V Л ) – лаг «опережает» – поправка лага л% - отрицательная. Поправка относительного лага л% - относительная суммарная системати-ческая погрешность лага, взятая с обратным знаком: k Л = V O / V Л ; Коэффициент относительного лага: л%=[(Vo – Vл) / Vл] ·100%; л% = 100 · (k Л – 1).
Слайд 56: Расчет пройденного кораблем расстояния
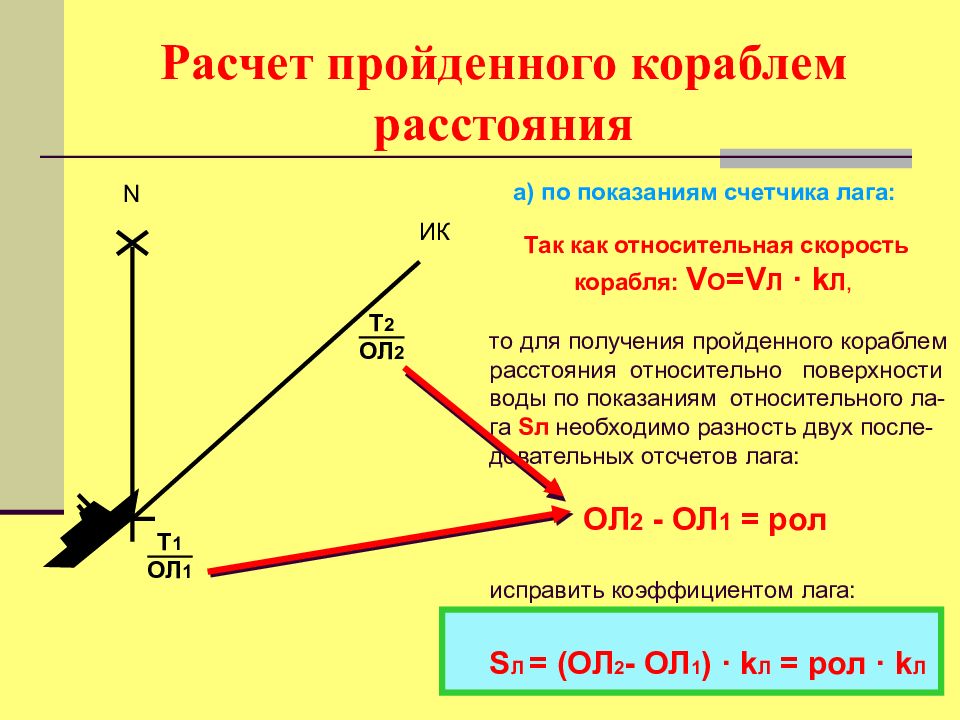
а) по показаниям счетчика лага: N ИК Т 1 ОЛ 1 Т 2 ОЛ 2 Так как относительная скорость корабля: V O =V Л · k Л, то для получения пройденного кораблем расстояния относительно поверхности воды по показаниям относительного ла-га Sл необходимо разность двух после-довательных отсчетов лага: ОЛ 2 - ОЛ 1 = рол исправить коэффициентом лага: S Л = (ОЛ 2 - ОЛ 1 ) · k Л = рол · k Л
Слайд 57: Расчет пройденного кораблем расстояния
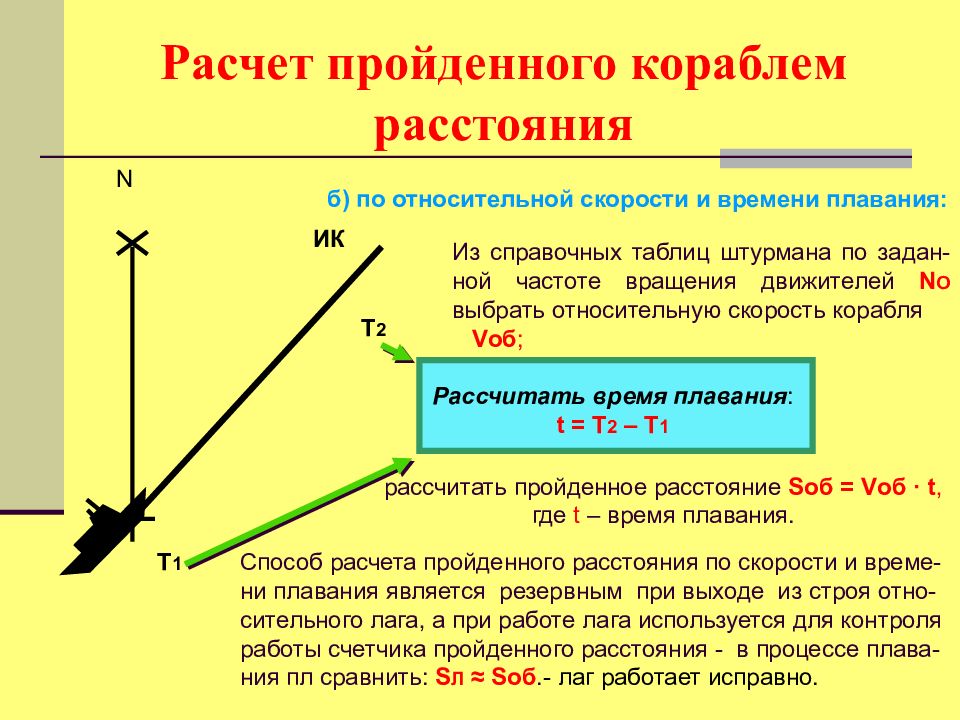
б) по относительной скорости и времени плавания: N ИК Т 1 Т 2 Из справочных таблиц штурмана по задан-ной частоте вращения движителей N O выбрать относительную скорость корабля Vоб ; Рассчитать время плавания : t = Т 2 – Т 1 рассчитать пройденное расстояние Sоб = Vоб · t, где t – время плавания. Способ расчета пройденного расстояния по скорости и време-ни плавания является резервным при выходе из строя отно-сительного лага, а при работе лага используется для контроля работы счетчика пройденного расстояния - в процессе плава-ния пл сравнить: S Л ≈ Sоб. - лаг работает исправно.
Слайд 58: Навигационные опасности. Средства навигационного оборудования
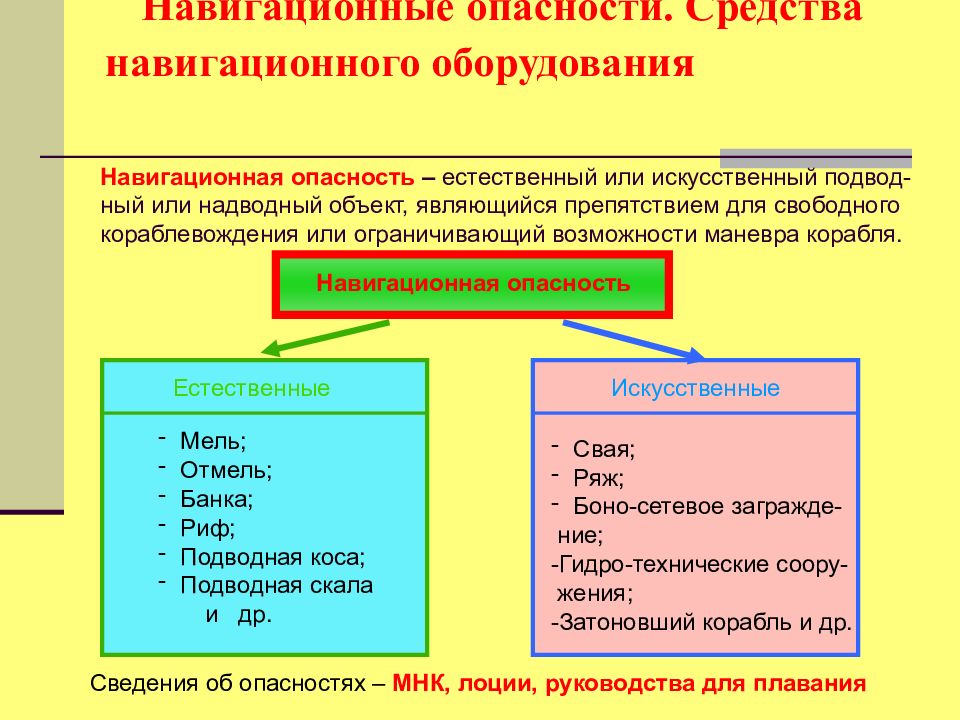
Навигационная опасность – естественный или искусственный подвод-ный или надводный объект, являющийся препятствием для свободного кораблевождения или ограничивающий возможности маневра корабля. Навигационная опасность Естественные Искусственные Мель; Отмель; Банка; Риф; Подводная коса; Подводная скала и др. Свая; Ряж; Боно-сетевое загражде- ние; -Гидро-технические соору- жения; -Затоновший корабль и др. Сведения об опасностях – МНК, лоции, руководства для плавания
Слайд 59: Средства навигационного оборудования
Средства навигационного оборудования (СНО) – специальные соору-жения, конструкции или устройства, предназначенные для ориентирования корабля или для определения его координат в море, а также для огражде-ния каналов, фарватеров и навигационных опасностей. Зрительные: маяки ( МК ), светящие (несветящие) знаки ( зн ) – используются для определения места корабля: маяк – сооружение башенного типа с даль-ностью видимости огня свыше 10 миль ; Маяк Кильдинский - Северный
Слайд 60: Средства навигационного оборудования
святящий знак – сооружение с дальностью види-мости огня менее 10 миль плавучие предостерегательные знаки (буи, вехи, бакены) – являются средствами ориентирования и используются для обозна - чения безопасных путей, навигационных опа - сностей, мест якорных и карантинных стоя - нок и т.п Буй Веха
Слайд 61: Средства навигационного оборудования
Звукосигнальные: наутофон ( нф ), сирена ( с ), колокол (к) и др. – используются для ориентирования в условиях ограниченной видимости и устанавливаются на маяках, знаках, буях. Радиотехнические: береговые РЛС, радиомаяки, радионавигацион-ные системы, спутниковые навигационные системы – используются для определения места корабля. Гидроакустические: гидроакустические навигационные системы, подводные звуковые маяки – используются для определения места пл. Электромагнитные: ведущие кабели – используются для обору-дования фарватеров.
Слайд 62: Дальность видимого горизонта в море
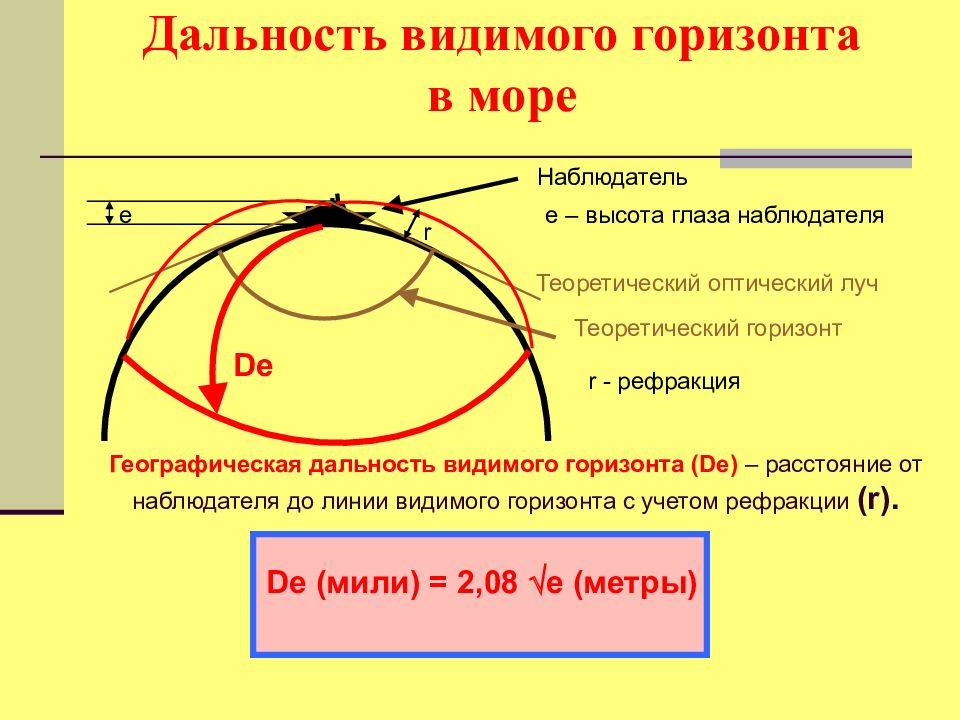
Наблюдатель е е – высота глаза наблюдателя Теоретический оптический луч Теоретический горизонт r r - рефракция De Географическая дальность видимого горизонта (De) – расстояние от наблюдателя до линии видимого горизонта с учетом рефракции (r). De (мили) = 2,08 е (метры)
Слайд 63: Дальность видимости ориентиров в море
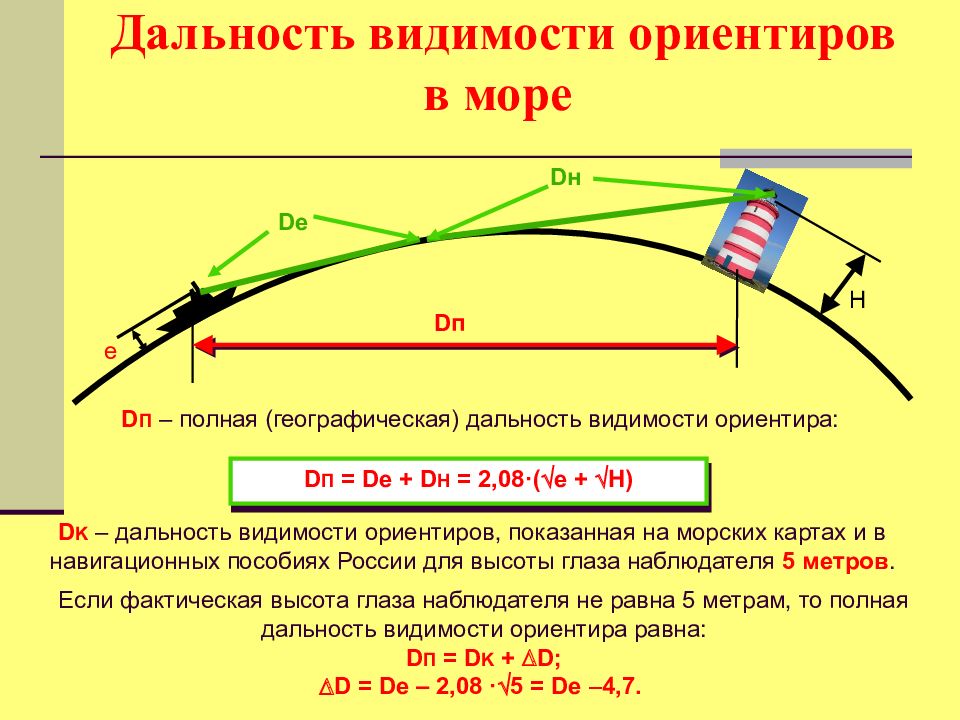
Н е De D н D п D П – полная (географическая) дальность видимости ориентира: D П = De + D H = 2,08·( e + H) D K – дальность видимости ориентиров, показанная на морских картах и в навигационных пособиях России для высоты глаза наблюдателя 5 метров. Если фактическая высота глаза наблюдателя не равна 5 метрам, то полная дальность видимости ориентира равна: D П = D K + D; D = D e – 2,08 · 5 = D e 4,7.
Слайд 64: Общие сведения о картографии
Карта – уменьшенное изображение земной поверхности на плоскости, выполненное по определенному математическому закону. План – карта ограниченного участка земной поверхности, полученная без искажений Объемное тело невозможно спроектировать на плоскость без искажений. Степень и характер искажений зависит от закона проектирования Земли на плоскость и проявляется в непостоянстве масштаба карты.
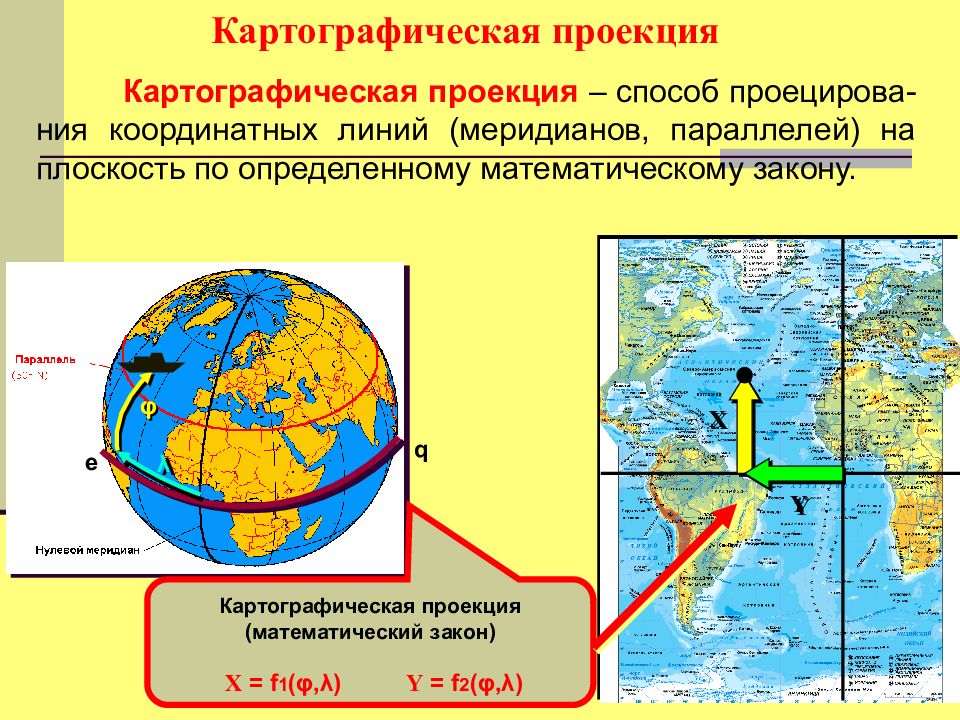
Слайд 65: Картографическая проекция
Картографическая проекция – способ проецирова - ния координатных линий (меридианов, параллелей) на плоскость по определенному математическому закону. q e Х Y φ λ Картографическая проекция (математический закон) X = f 1 ( φ, λ ) Y = f 2 ( φ, λ )
Слайд 66: Общие сведения о картографии
Картографическая сетка – система координатных линий (меридианов и параллелей), полученная при данной картографической проекции: косая – полюс системы координат отстоит от географического на угол от 0 до 90 . прямая – полюс системы координат совпадает с географическим полюсом Земли; поперечная – полюс системы координат отстоит от географического на угол 90 ;
Слайд 67: Общие сведения о картографии Классификация картографических проекций:
произвольные – проекции, обладающие специальными свойствами для решения конкретных задач. а) по характеру искажений: равноугольные – не искажают углов, сохраняют подобие фигур на местности и на карте; равновеликие – не искажают площадей, сохраняют пропорциональность площадей на местности и на карте; равнопромежуточные – проекции, сохраняющие постоянство масштаба по одному из направлений с экстремальным значением масштаба.
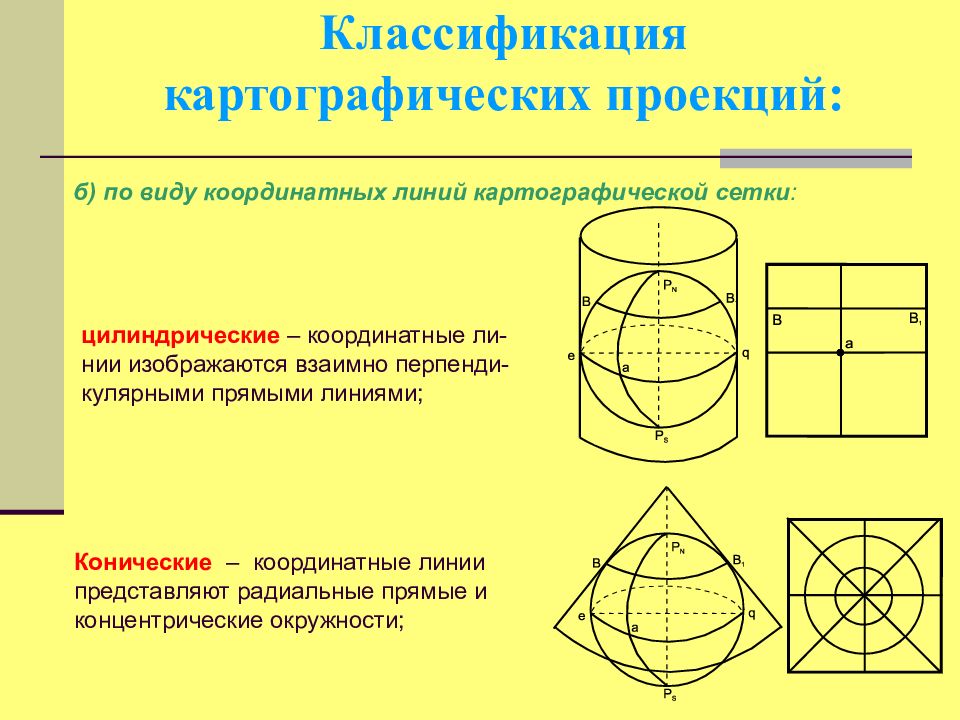
Слайд 68: Классификация картографических проекций:
б) по виду координатных линий картографической сетки : цилиндрические – координатные ли - нии изображаются взаимно перпенди - кулярными прямыми линиями; Конические – координатные линии представляют радиальные прямые и концентрические окружности;
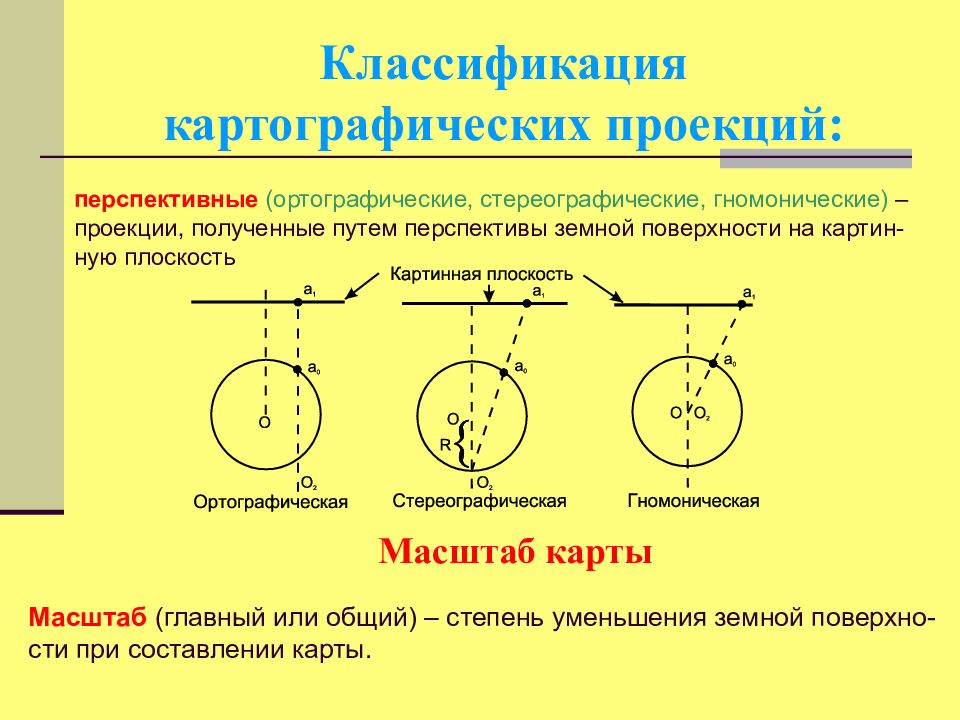
Слайд 69: Классификация картографических проекций:
перспективные (ортографические, стереографические, гномонические) – проекции, полученные путем перспективы земной поверхности на картин - ную плоскость Масштаб карты Масштаб (главный или общий) – степень уменьшения земной поверхно-сти при составлении карты.
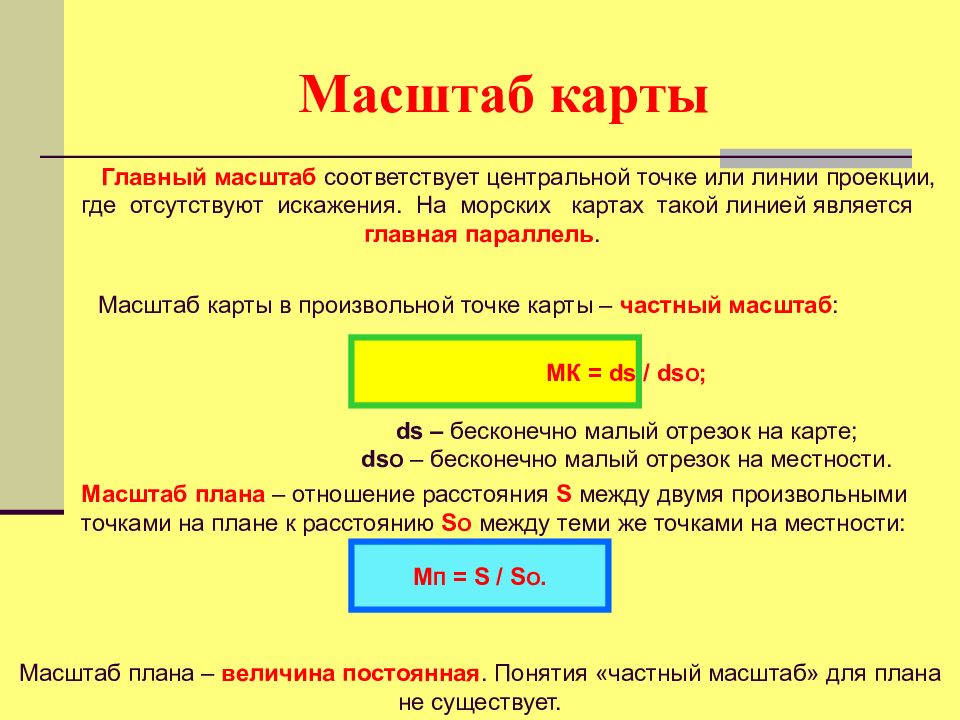
Слайд 70: Масштаб карты
М П = S / S O. МК = ds / ds O ; ds – бесконечно малый отрезок на карте; ds O – бесконечно малый отрезок на местности. Масштаб карты Главный масштаб соответствует центральной точке или линии проекции, где отсутствуют искажения. На морских картах такой линией является главная параллель. Масштаб плана – величина постоянная. Понятия «частный масштаб» для плана не существует. Масштаб карты в произвольной точке карты – частный масштаб : Масштаб плана – отношение расстояния S между двумя произвольными точками на плане к расстоянию S O между теми же точками на местности:
Слайд 71: Масштаб карты
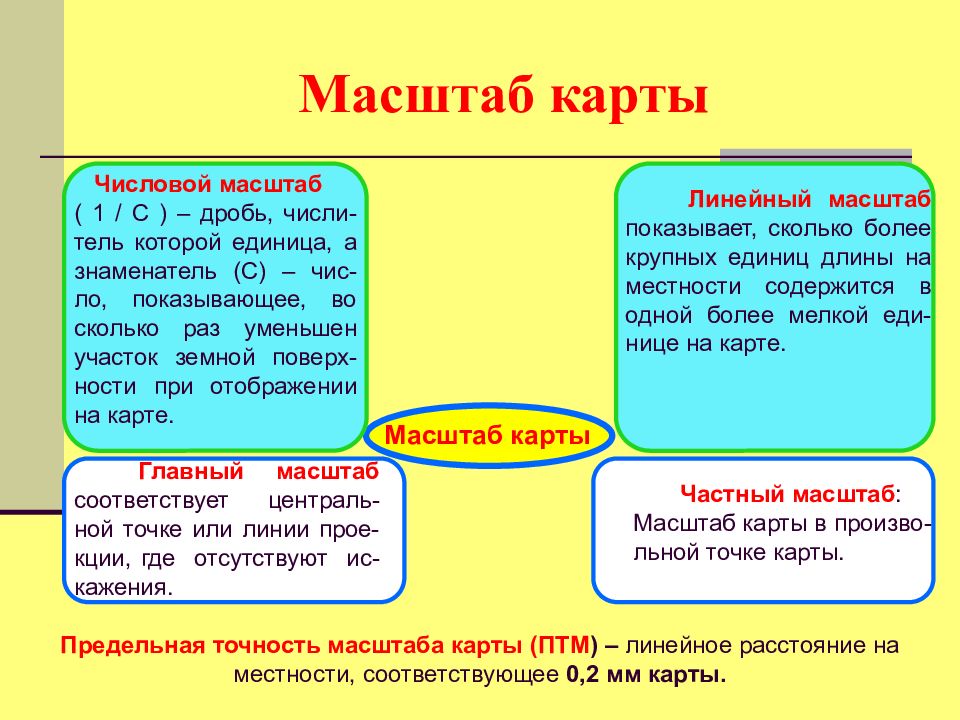
Масштаб карты Числовой масштаб ( 1 / С ) – дробь, числи - тель которой единица, а знаменатель (С) – чис - ло, показывающее, во сколько раз уменьшен участок земной поверх - ности при отображении на карте. Линейный масштаб показывает, сколько более крупных единиц длины на местности содержится в одной более мелкой еди-нице на карте. Главный масштаб соответствует централь-ной точке или линии прое-кции, где отсутствуют ис-кажения. Частный масштаб : Масштаб карты в произво-льной точке карты. Предельная точность масштаба карты (ПТМ ) – линейное расстояние на местности, соответствующее 0,2 мм карты.
Слайд 72: Прямая равноугольная цилиндрическая проекция Меркатора
При решении задач навигации возникает необходимость отображения на морской карте линии курса корабля (локсодромии), измерения и проклад-ки углов и направлений. Требования к МНК: 1. Локсодромия на карте должна изображаться прямой линией; 2. Углы, измеренные на местности, должны быть равны соответству-ющим углам, проложенным на карте, т.е. проекция должна быть рав-ноугольной. Указанным требованиям удовлетворяет прямая равноугольная цилиндрическая проекция, разра-ботанная в 1569 году голландским картографом Герардом Кремером (Меркатором).
Слайд 73: Принцип построения проекции Меркатора
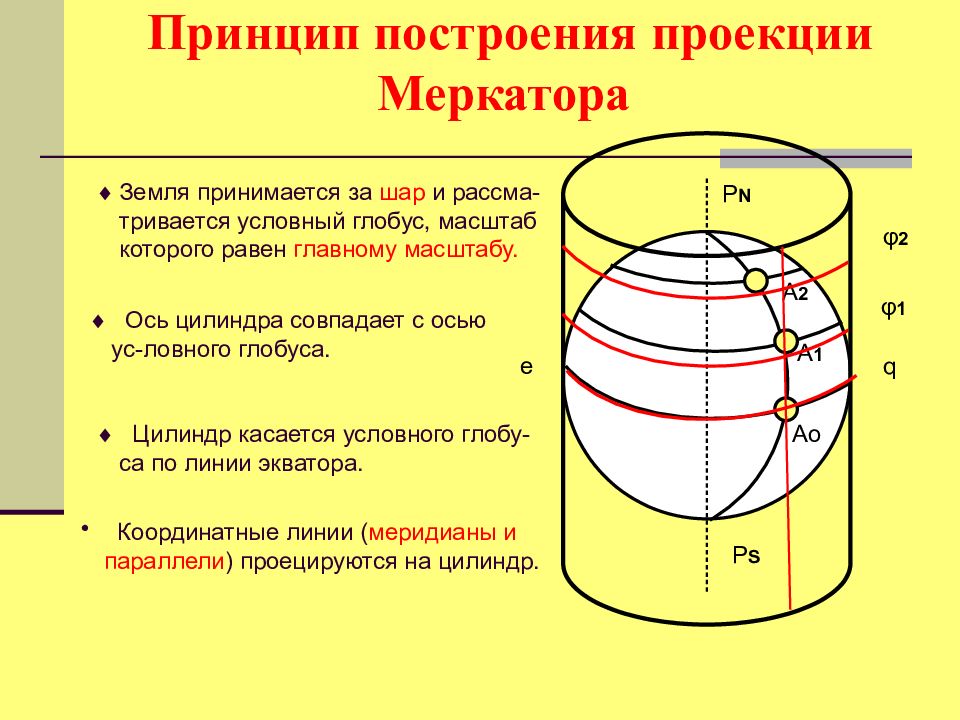
Земля принимается за шар и рассма-тривается условный глобус, масштаб которого равен главному масштабу. P N P S e q Ао А 1 А 2 Координатные линии ( меридианы и параллели ) проецируются на цилиндр. Ось цилиндра совпадает с осью ус-ловного глобуса. Цилиндр касается условного глобу-са по линии экватора. φ 1 φ 2
Слайд 74: Принцип построения проекции Меркатора
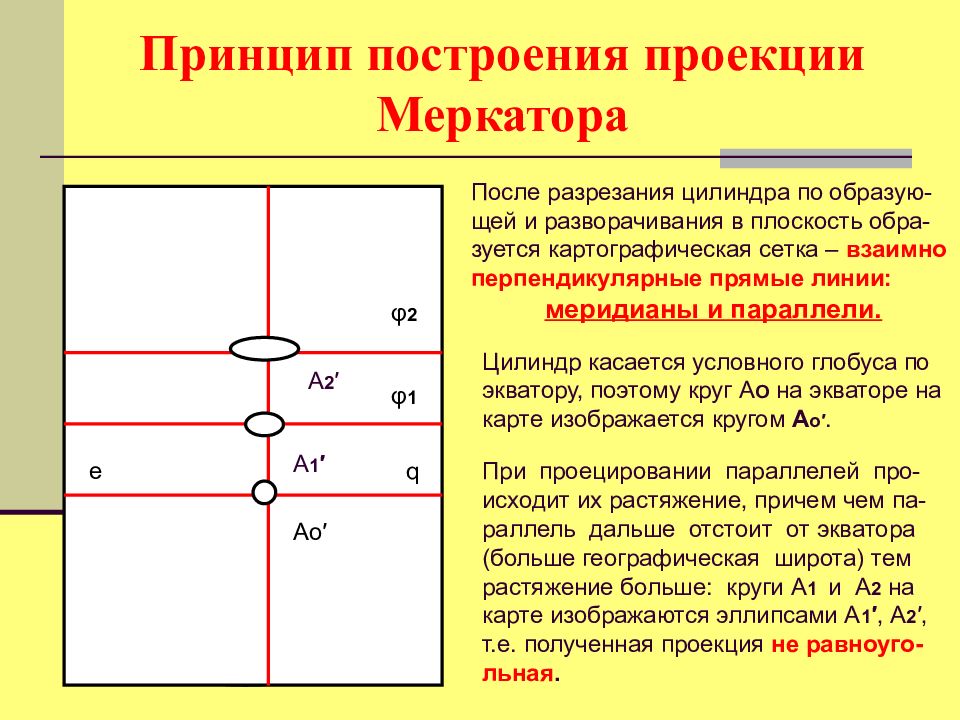
После разрезания цилиндра по образую - щей и разворачивания в плоскость обра - зуется картографическая сетка – взаимно перпендикулярные прямые линии: меридианы и параллели. Ао ′ Цилиндр касается условного глобуса по экватору, поэтому круг А О на экваторе на карте изображается кругом А о ′. При проецировании параллелей про-исходит их растяжение, причем чем па-раллель дальше отстоит от экватора (больше географическая широта) тем растяжение больше: круги А 1 и А 2 на карте изображаются эллипсами А 1 ′, А 2 ′, т.е. полученная проекция не равноуго-льная. А 1 ′ А 2 ′ φ 1 φ 2 e q
Слайд 75: Принцип построения проекции Меркатора
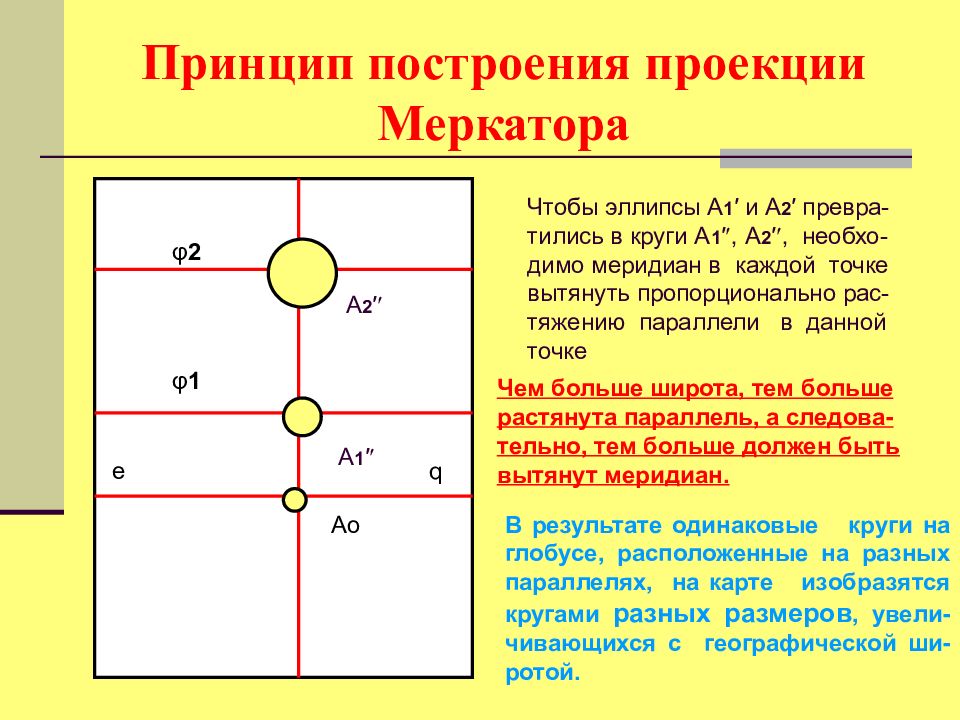
Чтобы эллипсы А 1 ′ и А 2 ′ превра - тились в круги А 1 ′ , А 2 ′ , необхо - димо меридиан в каждой точке вытянуть пропорционально рас - тяжению параллели в данной точке А 1 ′ Ao А 2 ′ Чем больше широта, тем больше растянута параллель, а следова - тельно, тем больше должен быть вытянут меридиан. В результате одинаковые круги на глобусе, расположенные на разных параллелях, на карте изобразятся кругами разных размеров, увели - чивающихся с географической ши - ротой. φ 2 φ 1 e q
Слайд 76: Принцип построения проекции Меркатора
Полученная таким образом проекция является: прямой – ось цилиндра совпадает с осью вращения Земли; равноугольной – элементарный круг на земной поверхности изображается на карте кругом (сохраняется подобие фигур); цилиндрической – картографическая сетка (меридианы и параллели) пред - ставляет собой взаимно перпендикулярные прямые линии. Уравнение проекции для шара имеет вид: x = R ln tg (45 + / 2 ), y = R . Графическое изображение на карте одной минуты дуги меридиана (морская миля) увеличивается с географической широтой. Следовательно, при измерении и прокладке расстояний необходимо ис - пользовать ту часть линейного масштаба карты, в широте которого осущест - вляется плавание корабля.
Последний слайд презентации: МОРСКОЙ КОРПУС ПЕТРА ВЕЛИКОГО САНКТ-ПЕТЕРБУРГСКИЙ ВОЕННО-МОРСКОЙ
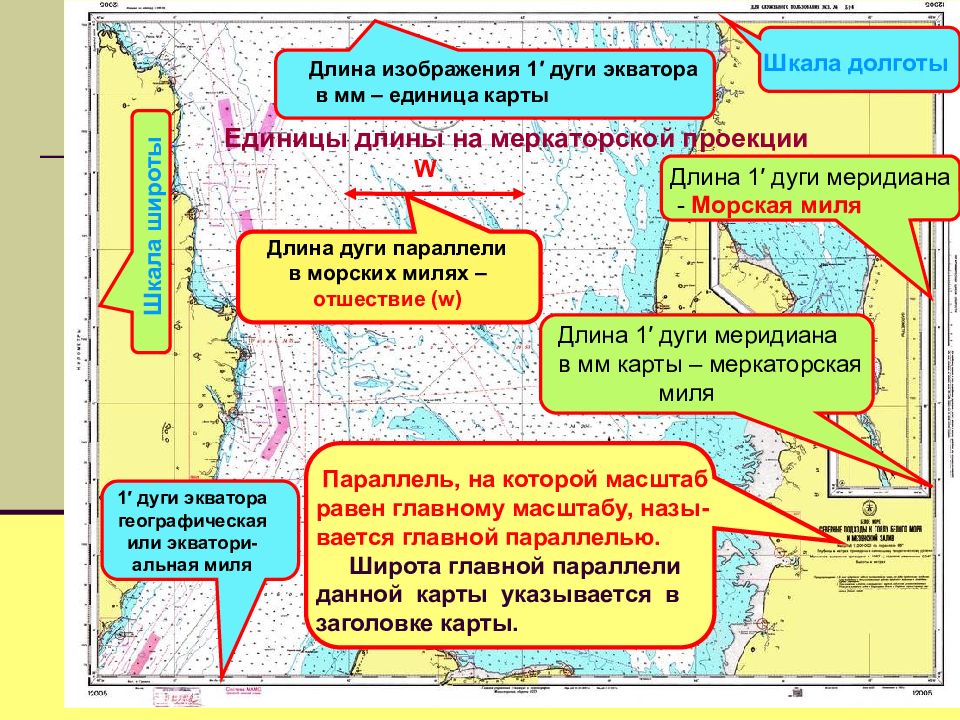
Единицы длины на меркаторской проекции Параллель, на которой масштаб равен главному масштабу, назы-вается главной параллелью. Широта главной параллели данной карты указывается в заголовке карты. Шкала широты Шкала долготы 1 ′ дуги экватора географическая или экватори- альная миля Длина изображения 1 ′ дуги экватора в мм – единица карты Длина 1 ′ дуги меридиана - Морская миля Длина 1′ дуги меридиана в мм карты – меркаторская миля Длина дуги параллели в морских милях – отшествие ( w) W