Разработала: Никулина Е.А. преподаватель БПОУ ВО «Череповецкий металлургический колледж имени академика И.П. Бардина»
Формы мышления и история развития алгебры логики История логики насчитывает около двух с половиной тысячелетий. Первые учения о формах и способах мышления возникли в Древнем Китае и Индии. Основоположником формальной логики является Аристотель (384-322 гг. до н.э.) – древнегреческий философ, который впервые отделил логические формы мышления от его содержания. Алгебра логики – наука об операциях, аналогичных математическим, над высказываниями или над объектами, которые могут принимать только два значения – «ИСТИНА» или «ЛОЖЬ». В 1842 году английский математик Джорж Буль разработал математическую логику или алгебру логики, которую впоследствии стали называть «булевой алгеброй». Спустя 100 лет алгебра логики стала основой теории цифровых вычислительных машин, ее используют в компьютерной логике, электронике, в основе всех микропроцессорных операций.
Формы мышления и история развития алгебры логики Многие философы и математики развивали отдельные положения логики и иногда даже намечали контуры современного исчисления высказываний, но ближе всех к созданию математической логики подошел уже во второй половине XVII века выдающийся немецкий ученый Готфрид Вильгельм Лейбниц (1646— 1716), указавший пути для перевода логики “из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются совершенно точно”. Лейбниц надеялся даже, что в будущем философы, вместо того чтобы бесплодно спорить, станут брать бумагу и вычислять, кто из них прав. При этом в своих работах Лейбниц затрагивал и двоичную систему счисления. Уже в XIX веке стало понятно, что система Буля хорошо подходит для описания электрических переключательных схем. Ток в цепи может либо протекать, либо отсутствовать, подобно тому, как утверждение может быть либо истинным, либо ложным. А еще несколько десятилетий спустя, уже в XX столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.
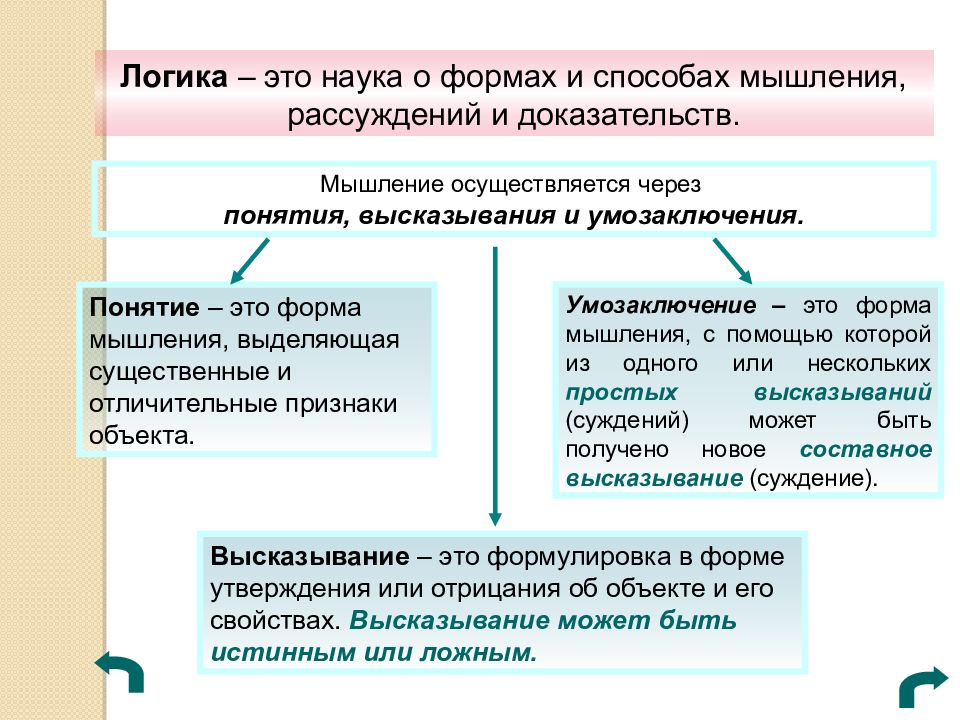
Логика – это наука о формах и способах мышления, рассуждений и доказательств. Мышление осуществляется через понятия, высказывания и умозаключения. Понятие – это форма мышления, выделяющая существенные и отличительные признаки объекта. Высказывание – это формулировка в форме утверждения или отрицания об объекте и его свойствах. Высказывание может быть истинным или ложным. Умозаключение – это форма мышления, с помощью которой из одного или нескольких простых высказываний (суждений) может быть получено новое составное высказывание (суждение).
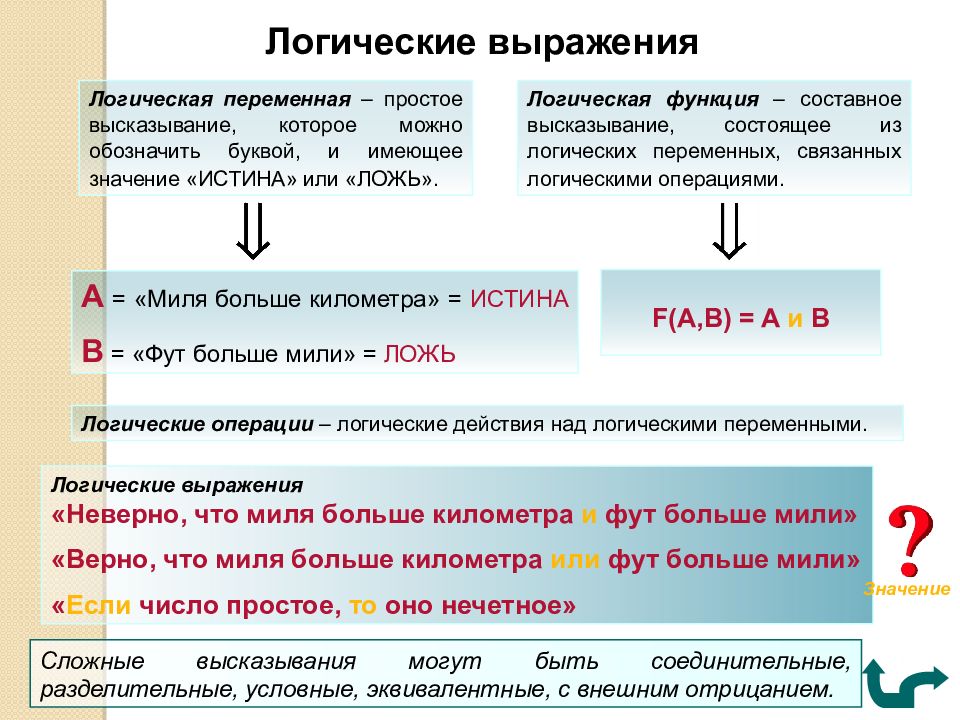
Логические выражения Логическая переменная – простое высказывание, которое можно обозначить буквой, и имеющее значение «ИСТИНА» или «ЛОЖЬ». Логическая функция – составное высказывание, состоящее из логических переменных, связанных логическими операциями. Логические операции – логические действия над логическими переменными. А = «Миля больше километра» = ИСТИНА В = «Фут больше мили» = ЛОЖЬ F(A,B) = A и В Логические выражения «Неверно, что миля больше километра и фут больше мили» «Верно, что миля больше километра или фут больше мили» « Если число простое, то оно нечетное» Сложные высказывания могут быть соединительные, разделительные, условные, эквивалентные, с внешним отрицанием. Значение
Логические операции НЕ,, Инверсия, логическое отрицание И,, and, &, *, · Конъюнкция, логическое умножение ИЛИ,, or, + Дизъюнкция, логическое сложение Импликация, логическое следование =, Эквивалентность, логическое равенство ИСТИНА – 1 ЛОЖЬ - 0 Таблица истинности определяет значение сложного высказывания при всех возможных значениях простых высказываний
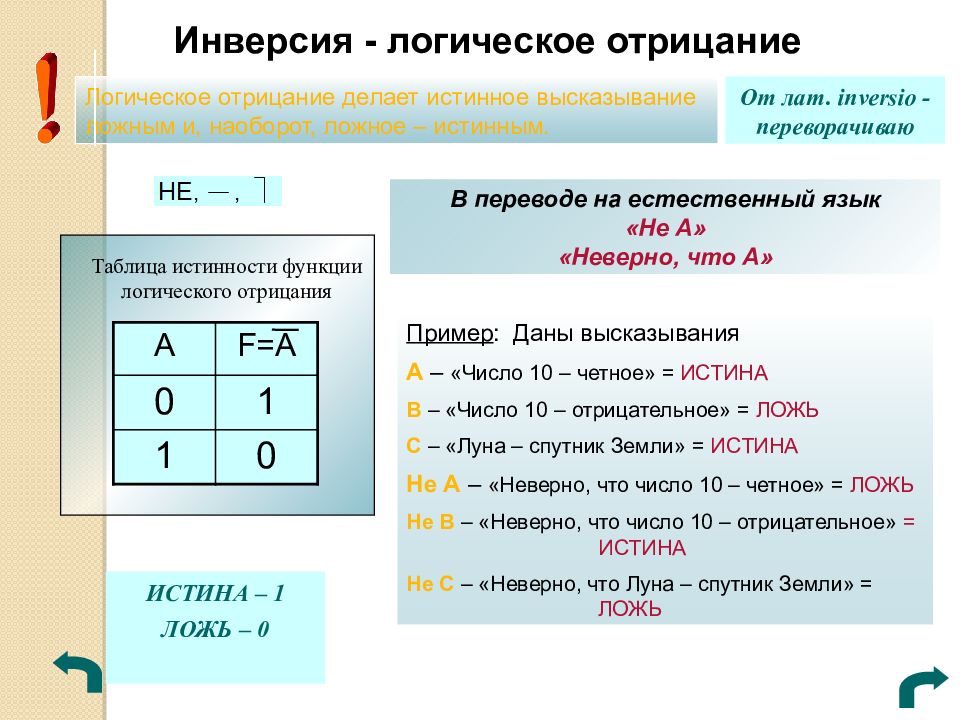
Инверсия - логическое отрицание От лат. inversio - переворачиваю Логическое отрицание делает истинное высказывание ложным и, наоборот, ложное – истинным. A F= А 0 1 1 0 Таблица истинности функции логического отрицания Пример : Даны высказывания А – «Число 10 – четное» = ИСТИНА В – «Число 10 – отрицательное» = ЛОЖЬ С – «Луна – спутник Земли» = ИСТИНА Не А – «Неверно, что число 10 – четное» = ЛОЖЬ Не В – «Неверно, что число 10 – отрицательное» = ИСТИНА Не С – «Неверно, что Луна – спутник Земли» = ЛОЖЬ В переводе на естественный язык «Не А» «Неверно, что А» ИСТИНА – 1 ЛОЖЬ – 0
Конъюнкция - логическое умножение От лат. conjunctio - связываю Результат логического умножения является истинным тогда и только тогда, когда истинны все входящие в него простые высказывания. Таблица истинности функции логического умножения A B F=A*B 0 0 0 0 1 0 1 0 0 1 1 1 В переводе на естественный язык «и А, и В» «как А, так и В» «А вместе с В» «А несмотря на В» «А, в то время как В» И,, and, &, *, · Пример : Даны высказывания А – «Число 10 – четное» = ИСТИНА В – «Число 10 – отрицательное» = ЛОЖЬ С – «Число 10 кратно 2» = ИСТИНА А и В – «Число 10 – четное и отрицательное» - ЛОЖЬ А и С – «Число 10 как четное, так и кратно 2» - ИСТИНА
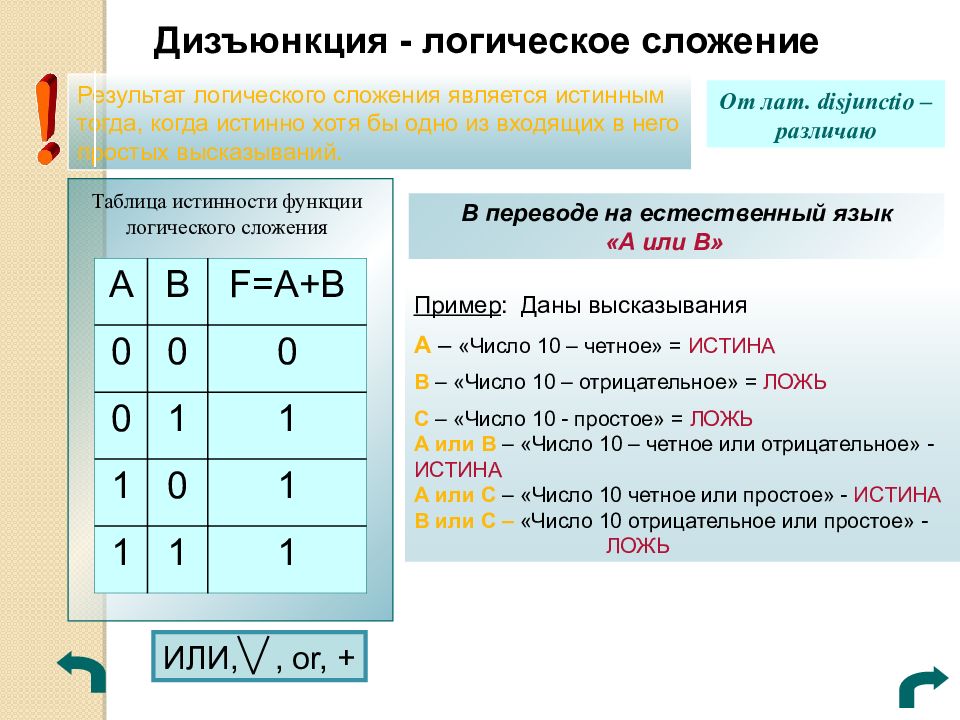
Дизъюнкция - логическое сложение От лат. disjunctio – различаю Результат логического сложения является истинным тогда, когда истинно хотя бы одно из входящих в него простых высказываний. В переводе на естественный язык «А или В» Таблица истинности функции логического сложения A B F=A + B 0 0 0 0 1 1 1 0 1 1 1 1 Пример : Даны высказывания А – «Число 10 – четное» = ИСТИНА В – «Число 10 – отрицательное» = ЛОЖЬ С – «Число 10 - простое» = ЛОЖЬ А или В – «Число 10 – четное или отрицательное» - ИСТИНА А или С – «Число 10 четное или простое» - ИСТИНА В или С – «Число 10 отрицательное или простое» - ЛОЖЬ ИЛИ,, or, +
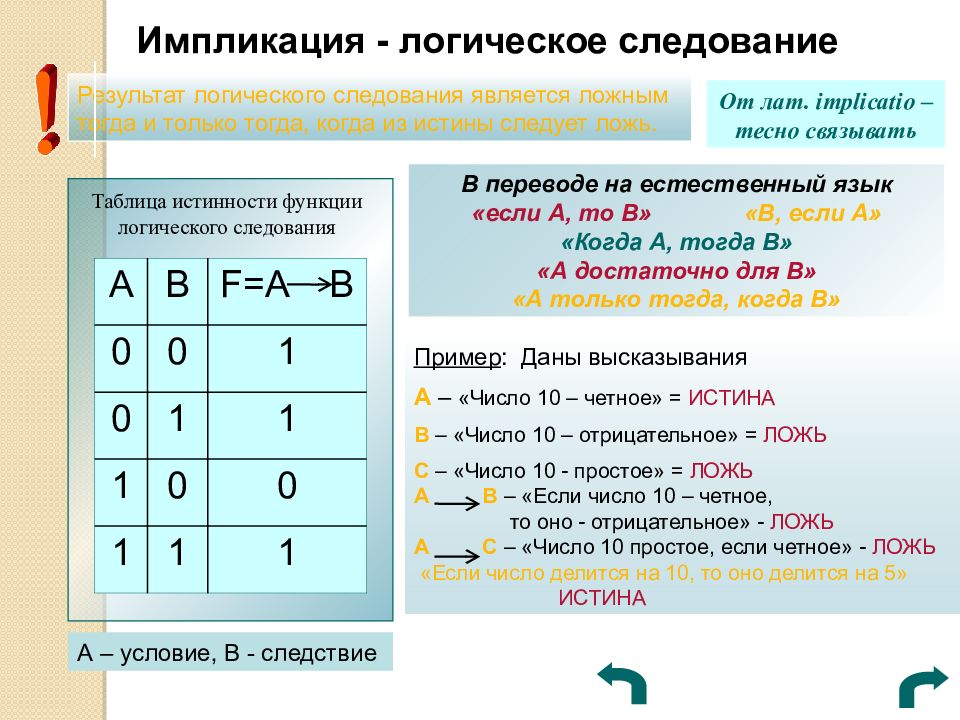
Импликация - логическое следование Результат логического следования является ложным тогда и только тогда, когда из истины следует ложь. От лат. implicatio – тесно связывать Таблица истинности функции логического следования A B F=A B 0 0 1 0 1 1 1 0 0 1 1 1 А – условие, В - следствие В переводе на естественный язык «если А, то В» «В, если А» «Когда А, тогда В» «А достаточно для В» «А только тогда, когда В» Пример : Даны высказывания А – «Число 10 – четное» = ИСТИНА В – «Число 10 – отрицательное» = ЛОЖЬ С – «Число 10 - простое» = ЛОЖЬ А В – «Если число 10 – четное, то оно - отрицательное» - ЛОЖЬ А С – «Число 10 простое, если четное» - ЛОЖЬ «Если число делится на 10, то оно делится на 5» ИСТИНА
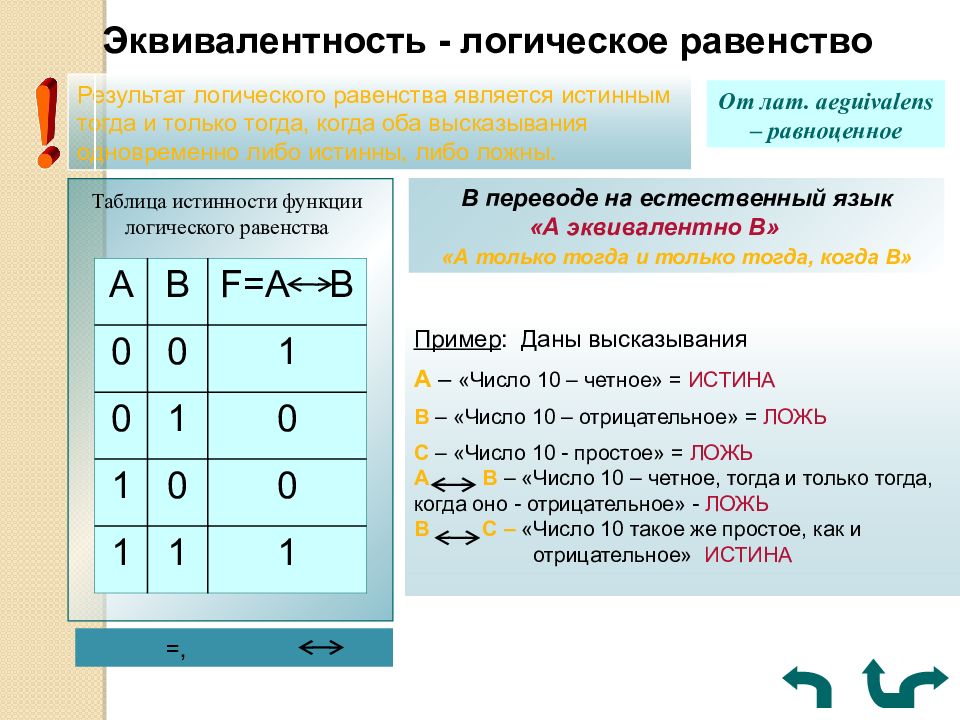
Эквивалентность - логическое равенство Результат логического равенства является истинным тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны. От лат. aeguivalens – равноценное Таблица истинности функции логического равенства A B F=A B 0 0 1 0 1 0 1 0 0 1 1 1 В переводе на естественный язык «А эквивалентно В» «А только тогда и только тогда, когда В» =, Пример : Даны высказывания А – «Число 10 – четное» = ИСТИНА В – «Число 10 – отрицательное» = ЛОЖЬ С – «Число 10 - простое» = ЛОЖЬ А В – «Число 10 – четное, тогда и только тогда, когда оно - отрицательное» - ЛОЖЬ В С – «Число 10 такое же простое, как и отрицательное» ИСТИНА
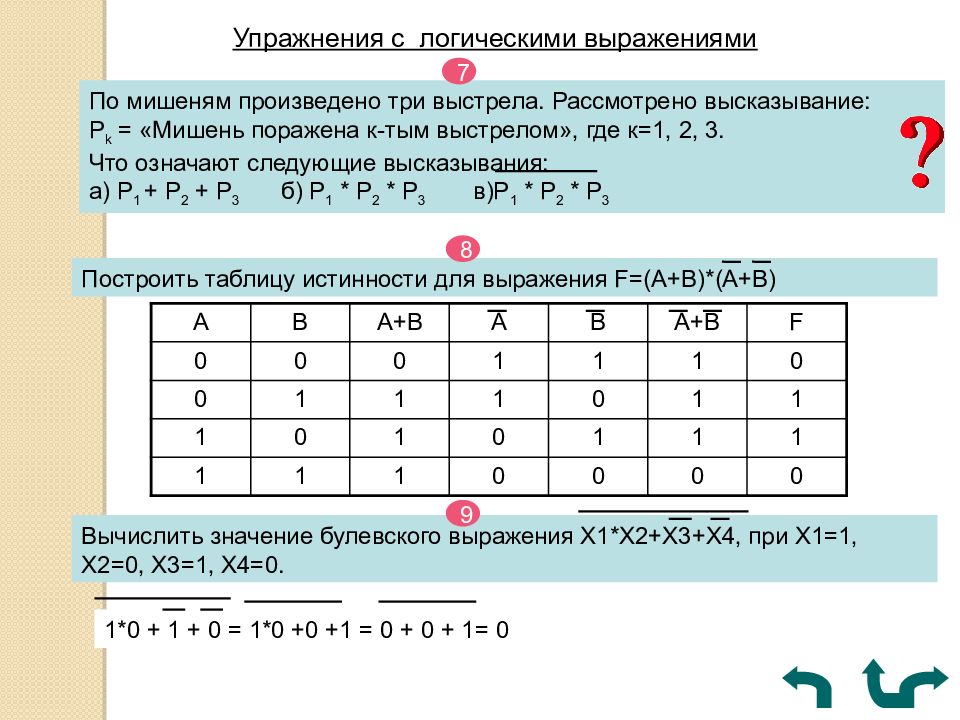
Упражнения c логическими выражениями По мишеням произведено три выстрела. Рассмотрено высказывание: P k = «Мишень поражена к-тым выстрелом», где к=1, 2, 3. Что означают следующие высказывания: а) P 1 + P 2 + P 3 б) P 1 * P 2 * P 3 в) P 1 * P 2 * P 3 7 Построить таблицу истинности для выражения F=(A+B)*(A+B) 8 А В А+В А В А+В F 0 0 0 1 1 1 0 0 1 1 1 0 1 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 Вычислить значение булевского выражения X1*X2+X3+X4, при X1=1, X2=0, X3=1, X4=0. 9 1*0 + 1 + 0 = 1*0 +0 +1 = 0 + 0 + 1= 0
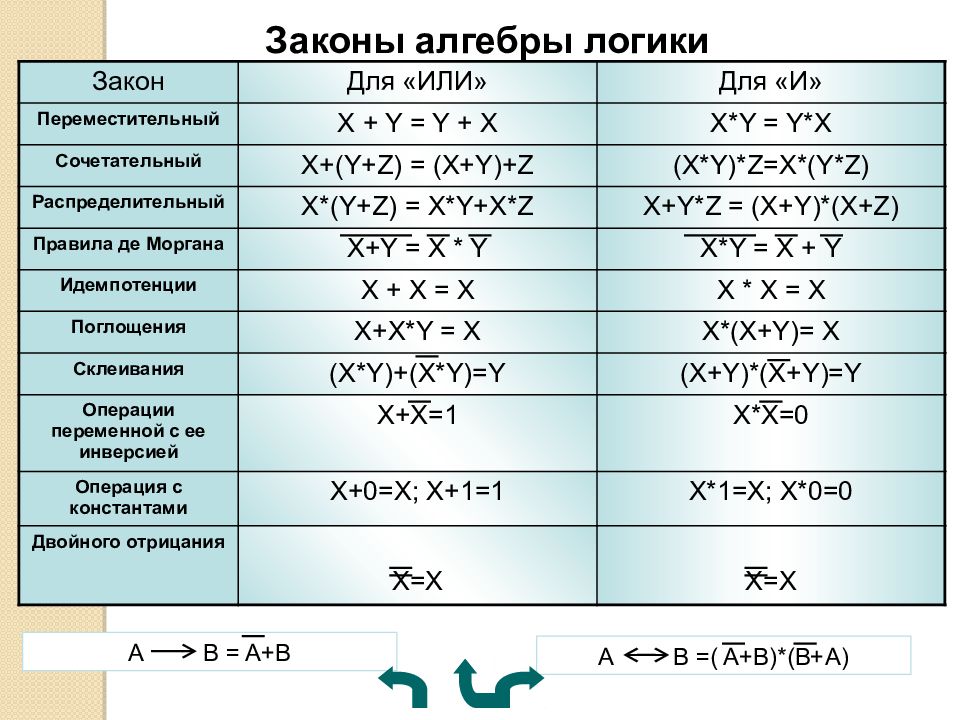
Законы алгебры логики Закон Для «ИЛИ» Для «И» Переместительный X + Y = Y + X X*Y = Y*X Сочетательный X+(Y+Z) = (X+Y)+Z (X*Y)*Z=X*(Y*Z) Распределительный X*(Y+Z) = X*Y+X*Z X+Y*Z = (X+Y)*(X+Z) Правила де Моргана X+Y = X * Y X*Y = X + Y Идемпотенции X + X = X X * X = X Поглощения X+X*Y = X X*(X+Y)= X Склеивания (X*Y)+(X*Y)=Y (X+Y)*(X+Y)=Y Операции переменной с ее инверсией X+X=1 X*X=0 Операция с константами X+0=X; X+1=1 X*1=X; X*0=0 Двойного отрицания X=X X=X A B = A+B A B =( A+B)*(B+A)
Логические основы компьютера. Базовые логические элементы Логический элемент компьютера (вентиль) - это электронная схема, реализующая базовую логическую операцию и характеризующаяся наличием сигнала на входе и выходе элемента. С помощью базовых логических элементов можно реализовать любую логическую функцию, выполняющую арифметические операции или хранение информации. Обычно у вентилей от двух до восьми входов и один или два выхода. Состояние логических элементов характеризуется таблицей входов-выходов логических элементов. На входы логических элементов подаются электрические сигналы высокого уровня напряжения (+5 вольт) – «логическая 1», и низкого уровня напряжения (около 0 вольт) – «логический 0» И (конъюнктор), ИЛИ (дизъюнктор), НЕ (инвертор) Чтобы построить логическую схему необходимо: 1) определить число логических переменных 2) определить количество базовых логических операций и их порядок 3) выбрать вентиль для каждой операции и соединить их в порядке выполнения логических операций.
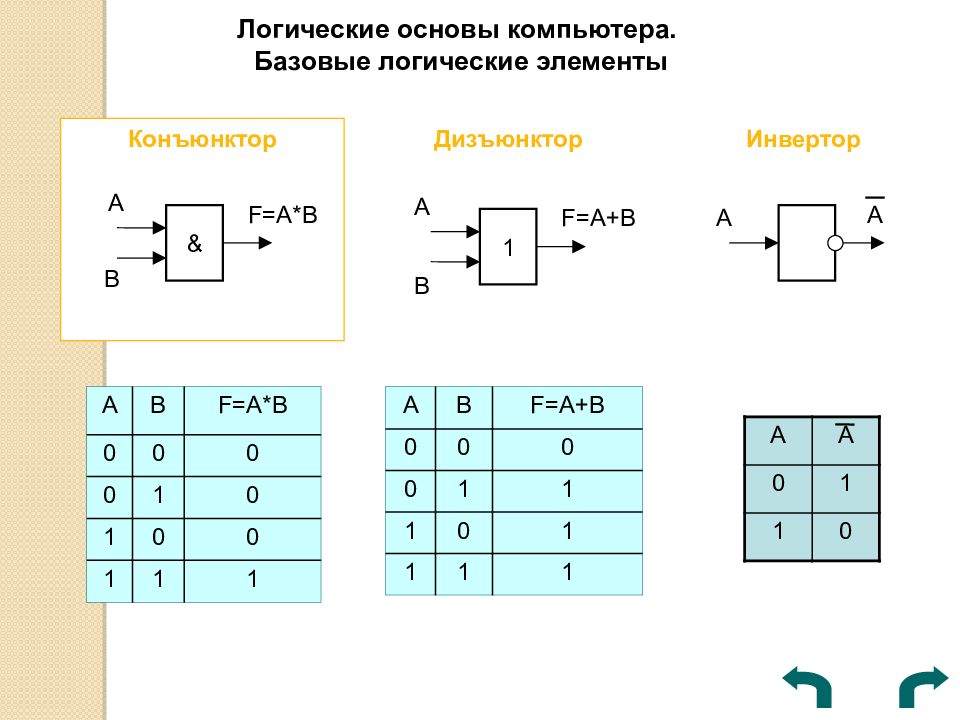
Конъюнктор Логические основы компьютера. Базовые логические элементы Дизъюнктор Инвертор & А В F= А*В 1 А В F= А + В А А A A 0 1 1 0 A B F=A*B 0 0 0 0 1 0 1 0 0 1 1 1 A B F=A + B 0 0 0 0 1 1 1 0 1 1 1 1
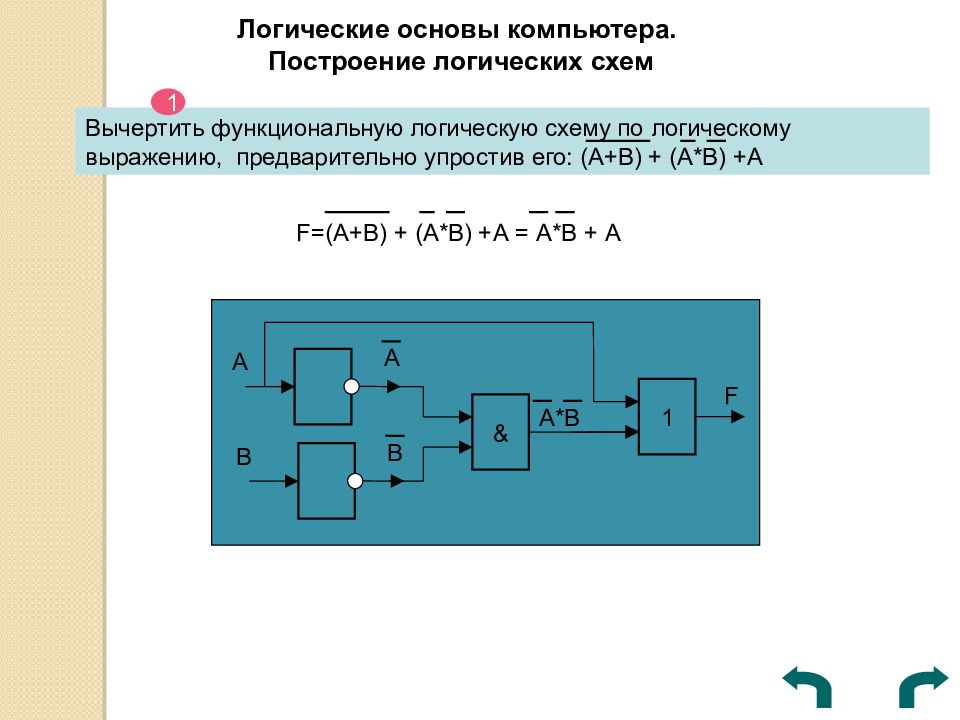
Логические основы компьютера. Построение логических схем Вычертить функциональную логическую схему по логическому выражению, предварительно упростив его: (А+В) + (А*В) +А F= (А+В) + (А*В) +А = А*В + А 1 А А В В & А*В 1 F
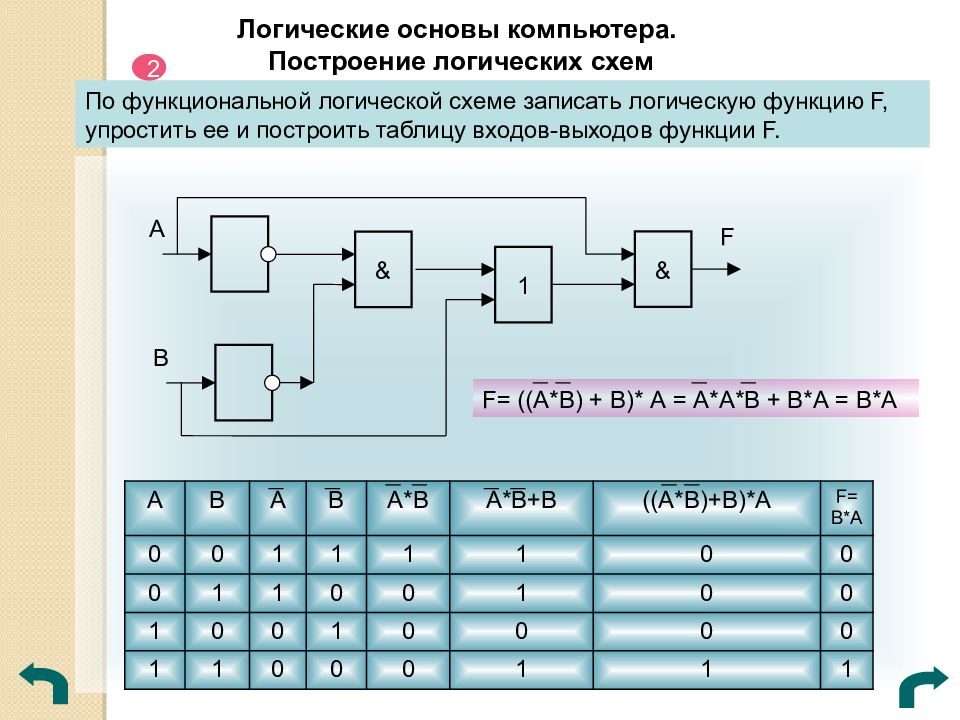
Логические основы компьютера. Построение логических схем По функциональной логической схеме записать логическую функцию F, упростить ее и построить таблицу входов-выходов функции F. А В & 1 & F F= ((А*В) + В)* А = А*А*В + В*А = В*А А В А В А*В А*В+В (( А*В)+В)*А F =В*А 0 0 1 1 1 1 0 0 0 1 1 0 0 1 0 0 1 0 0 1 0 0 0 0 1 1 0 0 0 1 1 1 2
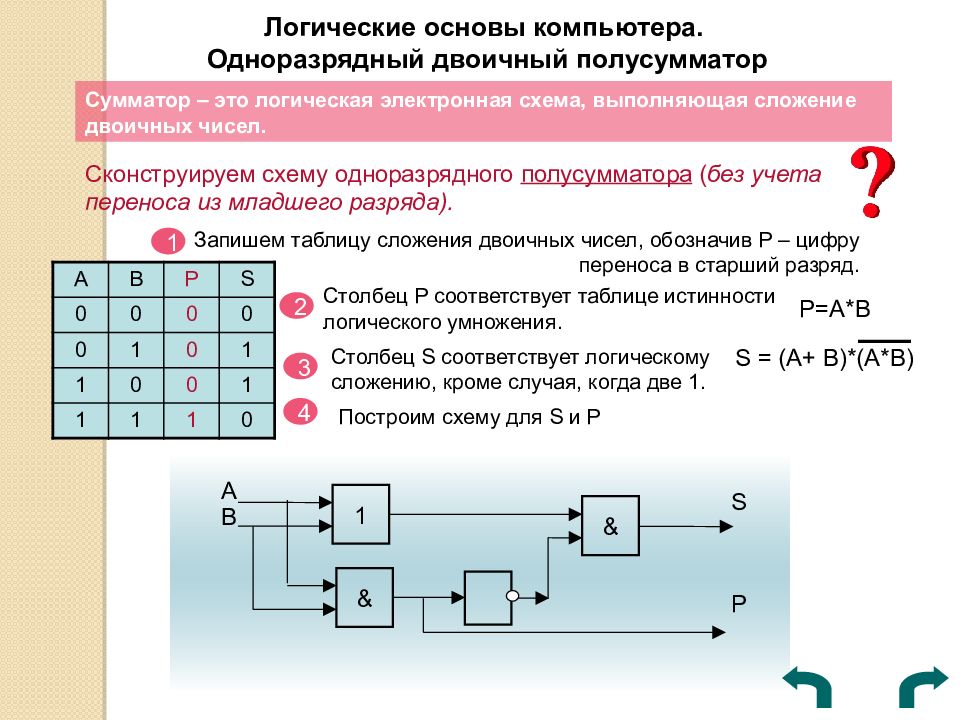
Логические основы компьютера. Одноразрядный двоичный полусумматор Сумматор – это логическая электронная схема, выполняющая сложение двоичных чисел. Сконструируем схему одноразрядного полусумматора ( без учета переноса из младшего разряда). Запишем таблицу сложения двоичных чисел, обозначив Р – цифру переноса в старший разряд. 1 А В P S 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 2 Столбец Р соответствует таблице истинности логического умножения. 3 Столбец S соответствует логическому сложению, кроме случая, когда две 1. S = (A+ B)*(A*B) 4 Построим схему для S и P Р=А*В A & 1 B & S P
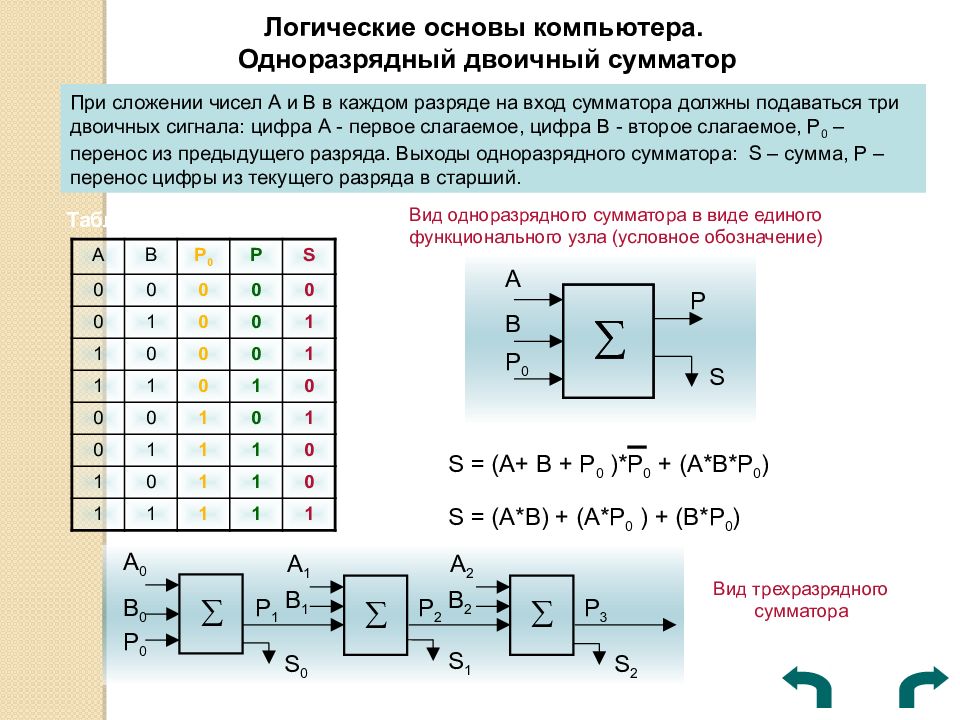
Логические основы компьютера. Одноразрядный двоичный сумматор При сложении чисел А и В в каждом разряде на вход сумматора должны подаваться три двоичных сигнала: цифра А - первое слагаемое, цифра В - второе слагаемое, P 0 – перенос из предыдущего разряда. Выходы одноразрядного сумматора: S – сумма, Р – перенос цифры из текущего разряда в старший. А В Р 0 Р S 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 0 1 0 1 0 1 1 1 0 1 0 1 1 0 1 1 1 1 1 Таблица входов-выходов Вид одноразрядного сумматора в виде единого функционального узла (условное обозначение) В А Р 0 Р S S = (A+ B + Р 0 )* Р 0 + (A*B *Р 0 ) S = (A * B ) + (А*Р 0 ) + (B *Р 0 ) А 0 В 0 Р 0 Р 1 S 0 А 1 В 1 S 1 Р 2 А 2 В 2 Р 3 S 2 Вид трехразрядного сумматора
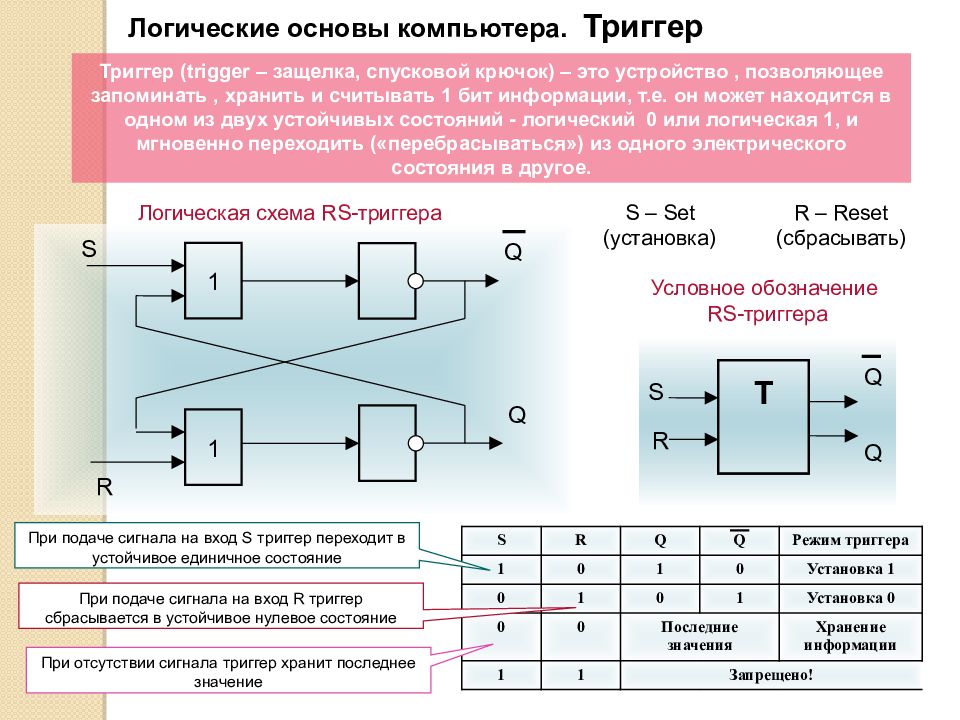
Логические основы компьютера. Триггер Триггер ( trigger – защелка, спусковой крючок) – это устройство, позволяющее запоминать, хранить и считывать 1 бит информации, т.е. он может находится в одном из двух устойчивых состояний - логический 0 или логическая 1, и мгновенно переходить («перебрасываться») из одного электрического состояния в другое. Логическая схема RS -триггера Условное обозначение RS -триггера R S Q T Q 1 1 S R Q Q S – Set ( установка) R – Reset ( сбрасывать) S R Q Q Режим триггера 1 0 1 0 Установка 1 0 1 0 1 Установка 0 0 0 Последние значения Хранение информации 1 1 Запрещено! При подаче сигнала на вход S триггер переходит в устойчивое единичное состояние При подаче сигнала на вход R триггер сбрасывается в устойчивое нулевое состояние При отсутствии сигнала триггер хранит последнее значение
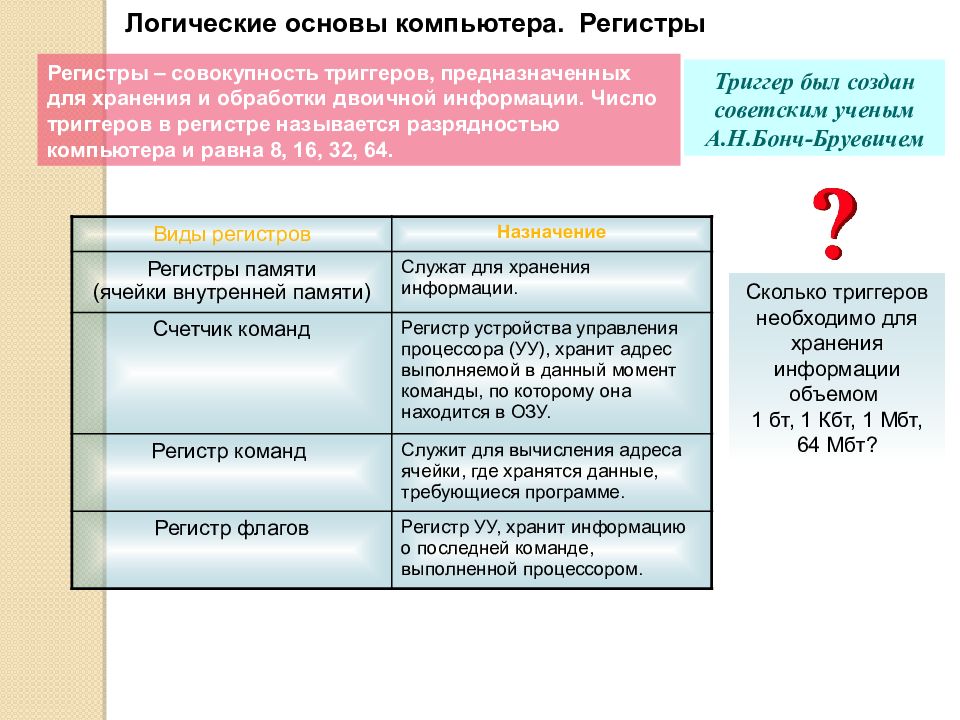
Логические основы компьютера. Регистры Триггер был создан советским ученым А.Н.Бонч-Бруевичем Сколько триггеров необходимо для хранения информации объемом 1 бт, 1 Кбт, 1 Мбт, 64 Мбт? Регистры – совокупность триггеров, предназначенных для хранения и обработки двоичной информации. Число триггеров в регистре называется разрядностью компьютера и равна 8, 16, 32, 64. Виды регистров Назначение Регистры памяти (ячейки внутренней памяти) Служат для хранения информации. Счетчик команд Регистр устройства управления процессора (УУ), хранит адрес выполняемой в данный момент команды, по которому она находится в ОЗУ. Регистр команд Служит для вычисления адреса ячейки, где хранятся данные, требующиеся программе. Регистр флагов Регистр УУ, хранит информацию о последней команде, выполненной процессором.
