Первый слайд презентации
Практикум №3 по решению стереометрических задач (базовый уровень)
Слайд 2
Задания №13 базового уровня на вычисление элементов составных многогранников и площади их поверхности
Слайд 3: Содержание
Задача №1 Задача №2 Задача №3 Задача №4 Задача №5 Задача №6 Задача №7 Задача №8 Задача №9 Задача №10 Задача №11 Задача №12 Задача №13 Задача №14 Задача №15 Задача №16 Задача №17 Задача №18 Задача №19 Задача №20 Задача №21 Задача №22 Задача №23 Для сам. реш.
Слайд 4: Задача №1
Найдите расстояние между вершинами А и С2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Решение. По теореме Пифагора имеем:
Слайд 5: Задача №2
Найдите квадрат расстояния между вершинами D и С2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Решение. Рассмотрим прямоуголь ный треугольник DD 2 C 2. По теореме Пифагора
Слайд 6: Задача №3
Найдите расстояние между вершинами В1 и D 2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Решение. Треугольник KD 2 B 1 = прямоуг. По теореме Пифагора :
Слайд 7: Задача №4
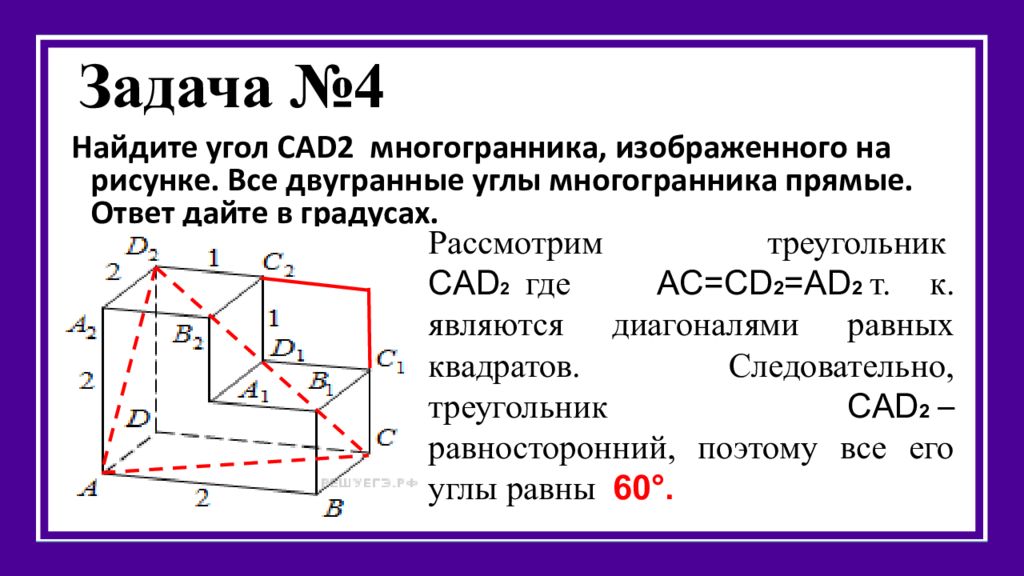
Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Решение. Рассмотрим треугольник CAD 2 где AC=CD 2 =AD 2 т. к. являются диагоналями равных квадратов. Следовательно, треугольник CAD 2 – равносторонний, поэтому все его углы равны 60 °.
Слайд 8: Задача №5
Найдите угол АВ D многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Решение. ABCD квадрат со стороной 2, а BD — его диагональ. Значит, треугольник ABD — прямоугольный и равнобедренный, AB=AD . Угол ABD равен 45 °
Слайд 9
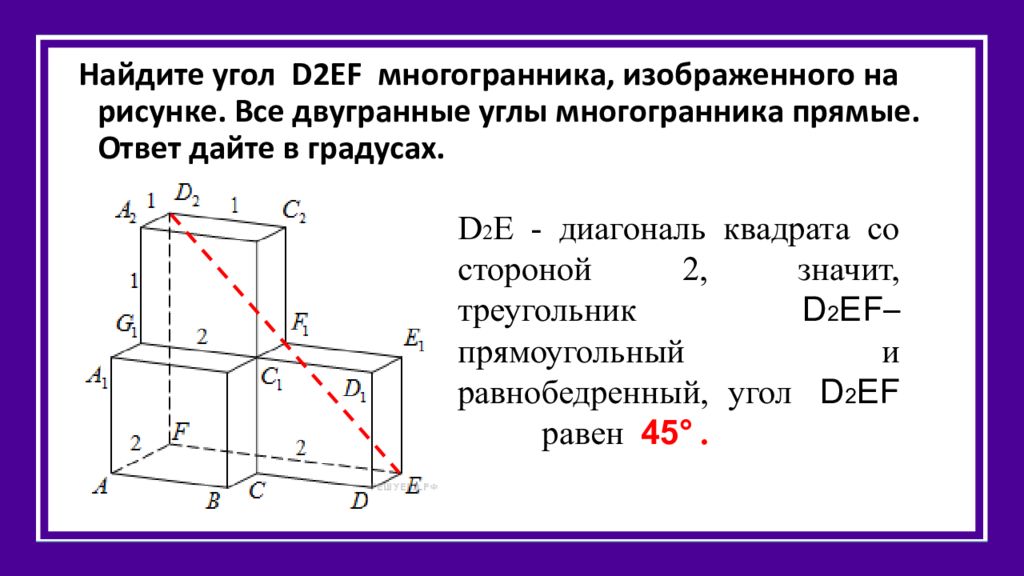
Найдите угол D2EF многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. D 2 E - диагональ квадрата со стороной 2, значит, треугольник D 2 EF – прямоугольный и равнобедренный, угол D 2 EF равен 45 ° .
Слайд 10
Найдите угол EAD 2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Рассмотрим треугольник EAD 2. В нем AE=ED 2 =D 2 A, т.к. это диагонали равных квадратов. Таким образом, треугольник EAD 2 — равносторонний, все его углы равны 60°.
Слайд 11: Задача № 8
Найдите тангенс угла В 2 А 2 С 2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Решение. Треугольник В 2 А 2 С 2 прямоугольный. Значит
Слайд 12
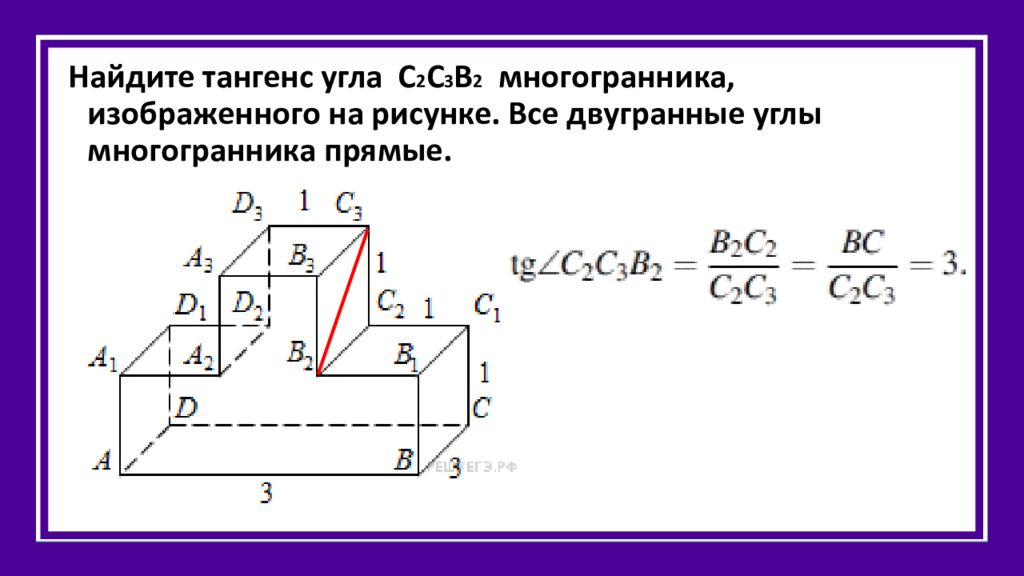
Найдите тангенс угла С 2 С 3 В 2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Слайд 13
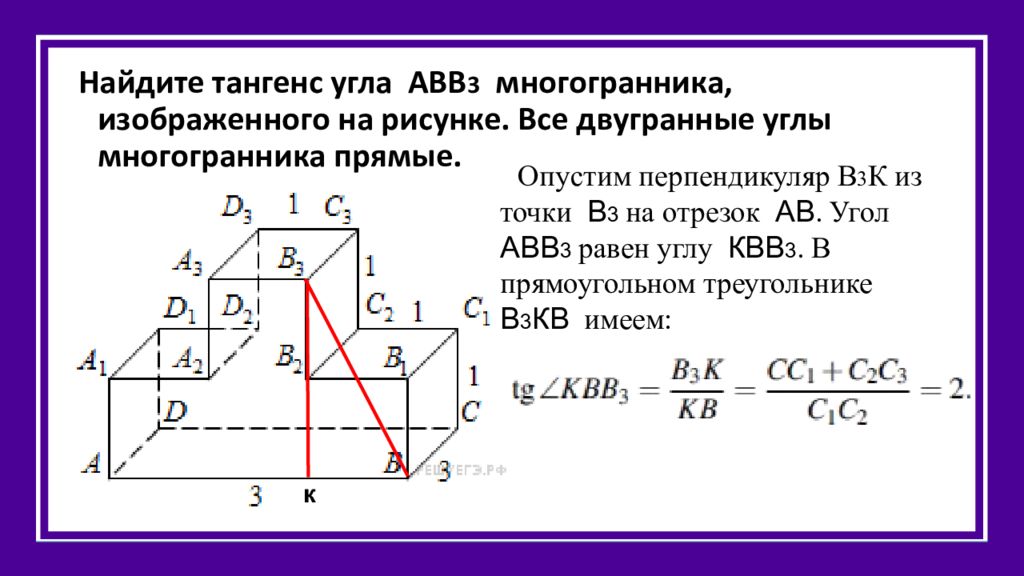
Найдите тангенс угла АВВ 3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. к Опустим перпендикуляр В 3 К из точки В 3 на отрезок АВ. Угол АВВ 3 равен углу КВВ 3. В прямоугольном треугольнике В 3 КВ имеем:
Слайд 14: Задача № 11
Найдите квадрат расстояния между вершинами В2 и D3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Решение. Ответ: 11
Слайд 15: Задача № 12
Найдите квадрат расстояния между вершинами В и D 2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Решение. Треугольник ВС1 D 2 прямоугольный =>
Слайд 16: Задача № 13
Найдите квадрат расстояния между вершинами А и С 3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Решение.
Слайд 17: Задача №1 4
Найдите квадрат расстояния между вершинами D и С 2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Слайд 18: Задача №15
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 2, 3, 1 и двух площадей прямоугольников со сторонами 2, 1 :
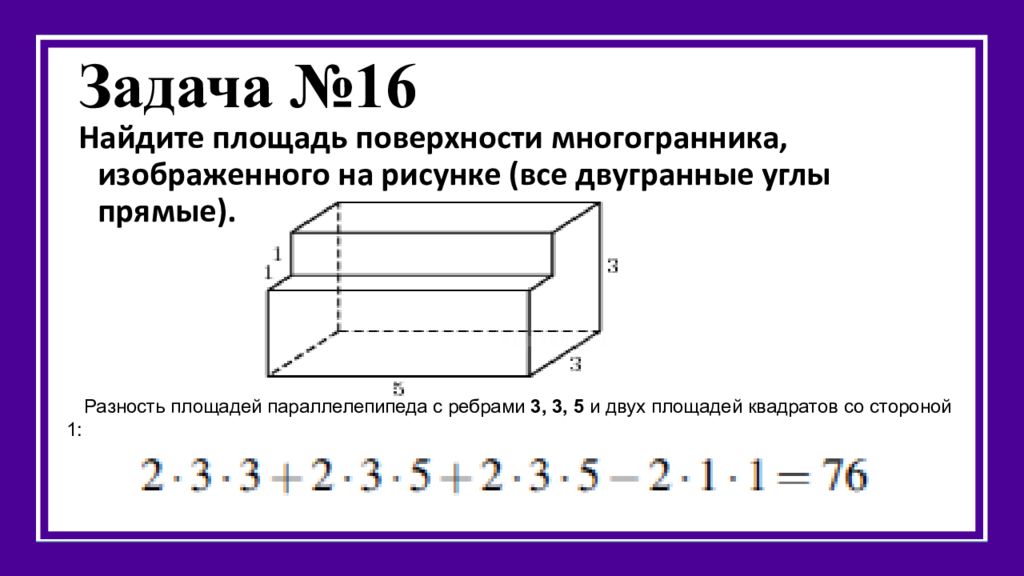
Слайд 19: Задача №16
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Разность площадей параллелепипеда с ребрами 3, 3, 5 и двух площадей квадратов со стороной 1:
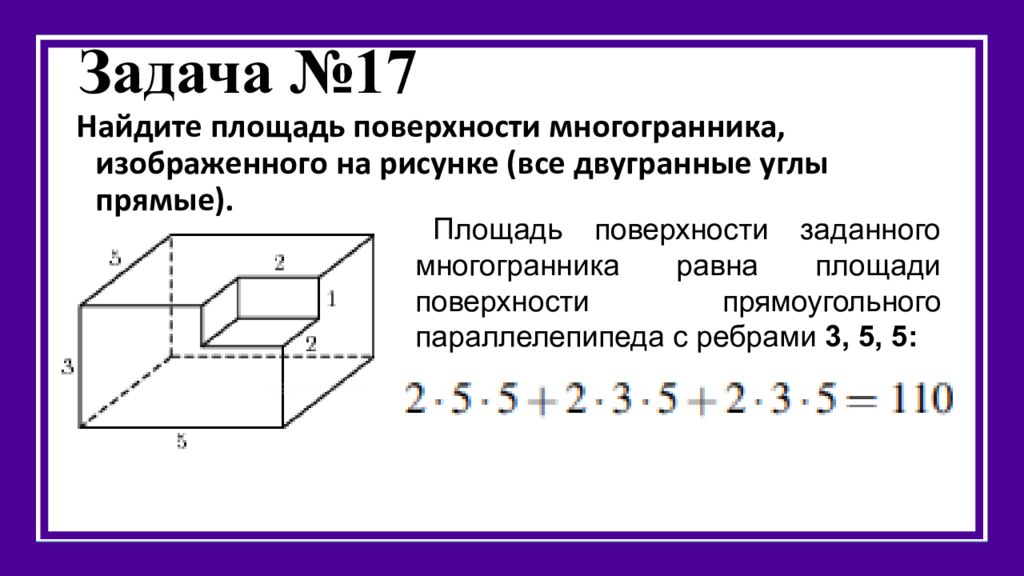
Слайд 20: Задача №17
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:
Слайд 21: Задача №18
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 4:
Слайд 22: Задача №19
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Площадь поверхности заданного многогранника равна сумме площадей большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького параллелепипеда, излишне учтенной при расчете площадей поверхности параллелепипедов :
Слайд 23: Задача №20
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Площадь поверхности тела равна сумме поверхностей трех составляющих ее параллелепипедов с ребрами 2,5,6 ; 2,5,3 и 2,2,3, уменьшенная на удвоенные площади прямоугольников со сторонами 5,3 и 2, 3:
Слайд 24: Задача №21
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Площадь поверхности данной детали - есть сумма площади поверхности двух многогранников: со сторонами 1,2,5 и 2,2,2 за вычетом 2 площадей прямоугольников со сторонами 2,2 (т. к. данная площадь учитывается два раза при сложении площадей многогранников, а как видно из рисунка, данных площадей в итоговой детали нет). Значит:
Слайд 25: Задача №22
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Площадь поверхности данной детали - есть площадь поверхности многогранника со сторонами 6,5,5 за вычетом площади двух "боковых прямоугольников" со сторонами 3,2 и прибавления 2 площадей "верхнего" и "нижнего прямоугольников" со сторонами 2,5. Получаем:
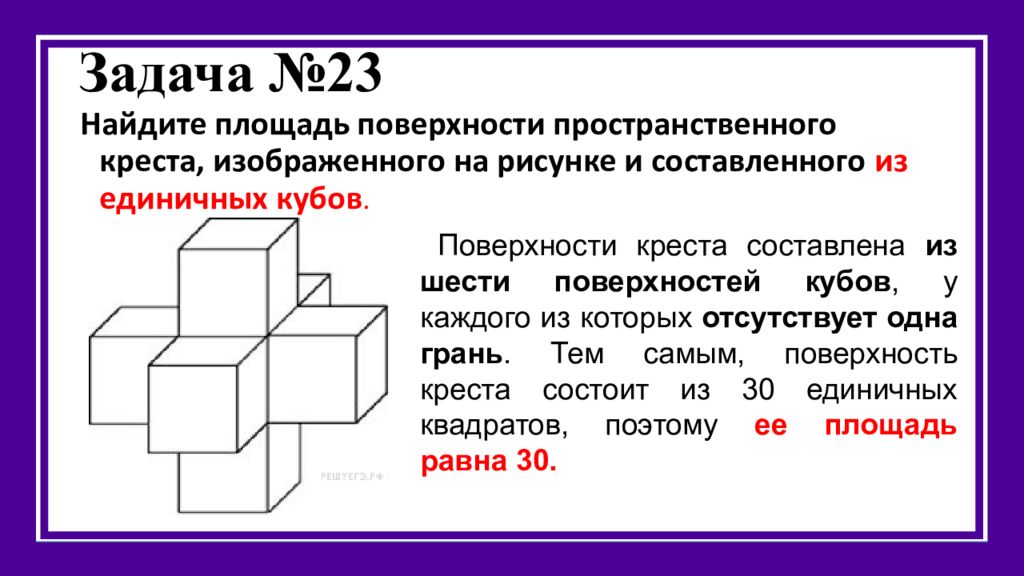
Слайд 26: Задача №23
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов. Поверхности креста составлена из шести поверхностей кубов, у каждого из которых отсутствует одна грань. Тем самым, поверхность креста состоит из 30 единичных квадратов, поэтому ее площадь равна 30.
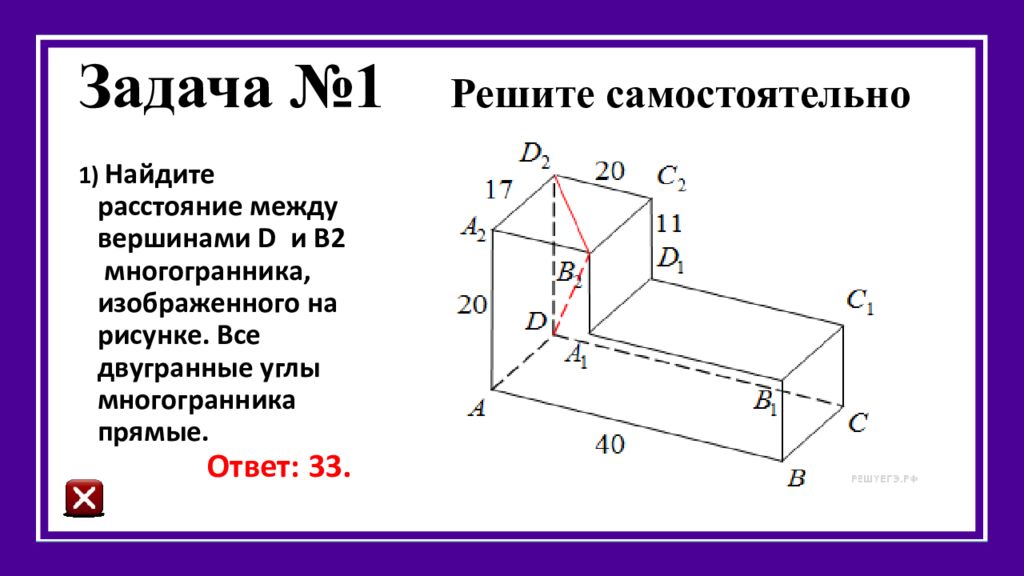
Слайд 28: Задача №1 Решите самостоятельно
1) Найдите расстояние между вершинами D и B 2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ: 33.
Слайд 29: Задача №1 Решите самостоятельно
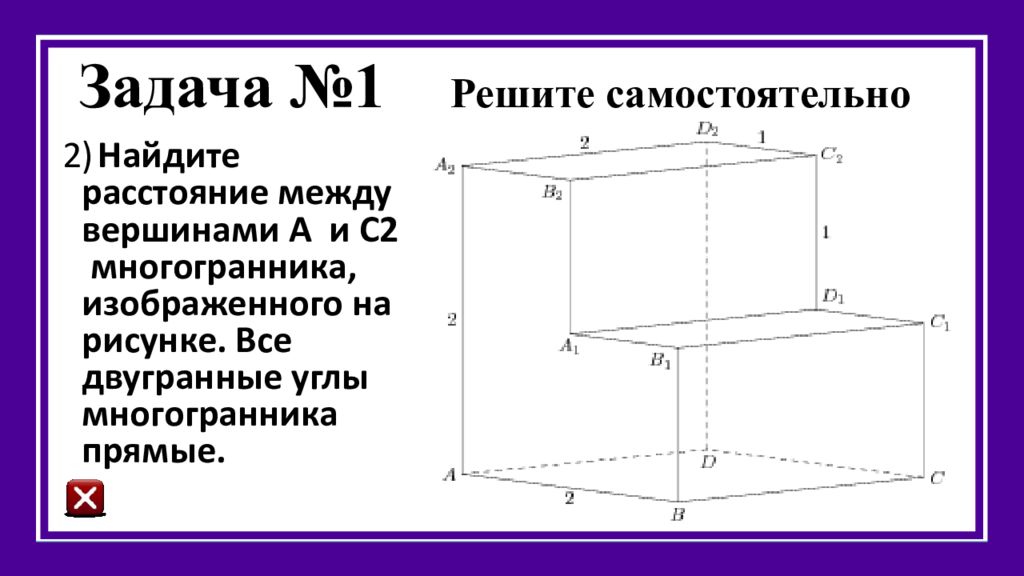
2) Найдите расстояние между вершинами А и С2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Слайд 30: Задача №1 Решите самостоятельно
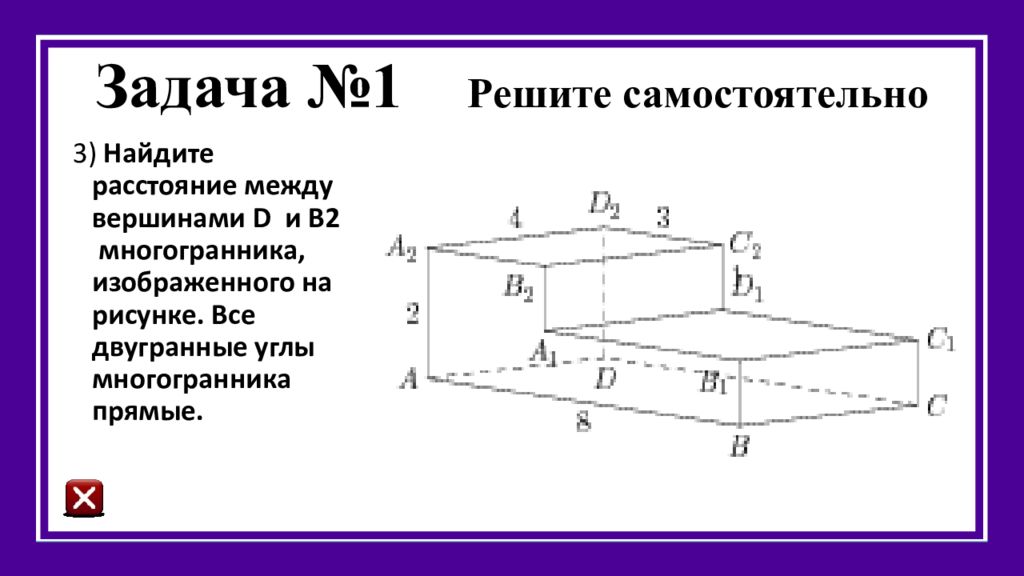
3) Найдите расстояние между вершинами D и B 2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Слайд 31: Задача №2 Решите самостоятельно
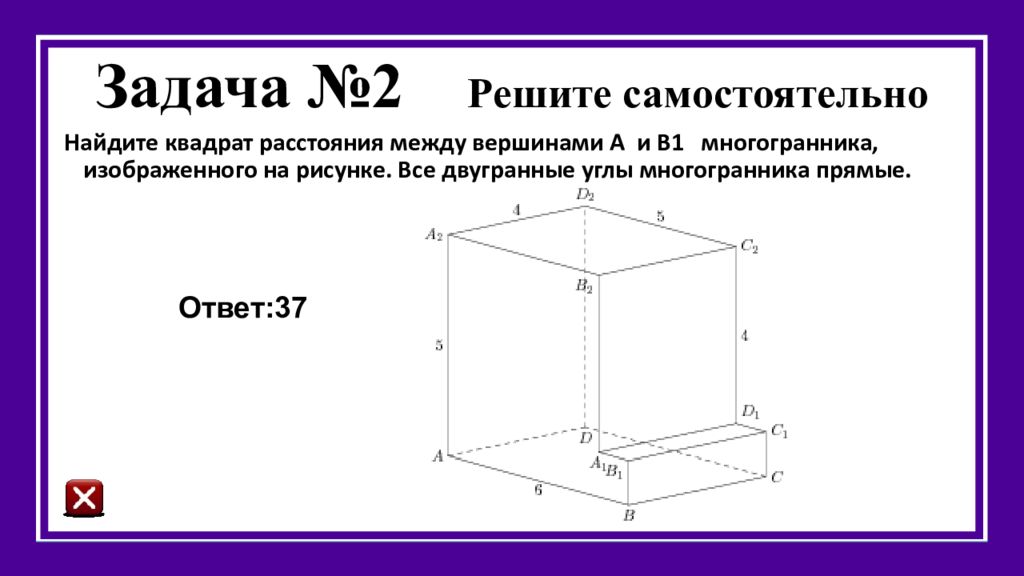
Найдите квадрат расстояния между вершинами А и В1 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ:37
Слайд 32: Задача №5 Решите самостоятельно
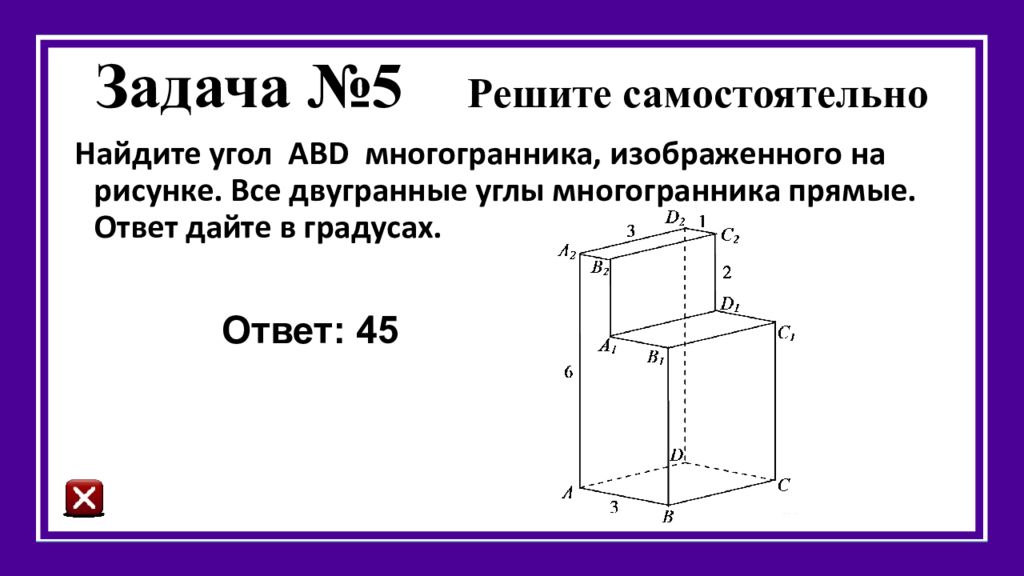
Найдите угол АВ D многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах. Ответ: 45
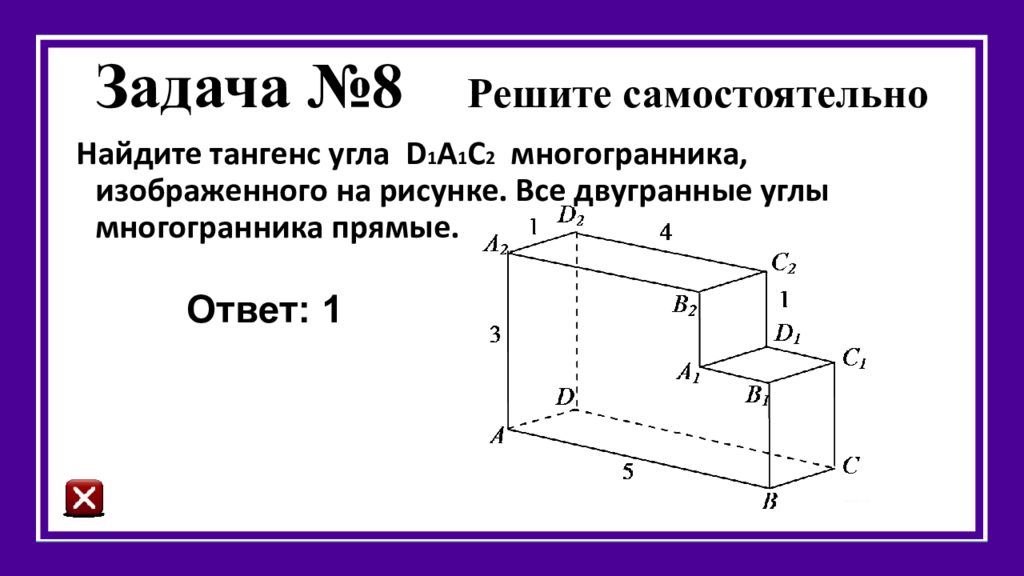
Слайд 33: Задача №8 Решите самостоятельно
Найдите тангенс угла D 1 А 1 С 2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ: 1
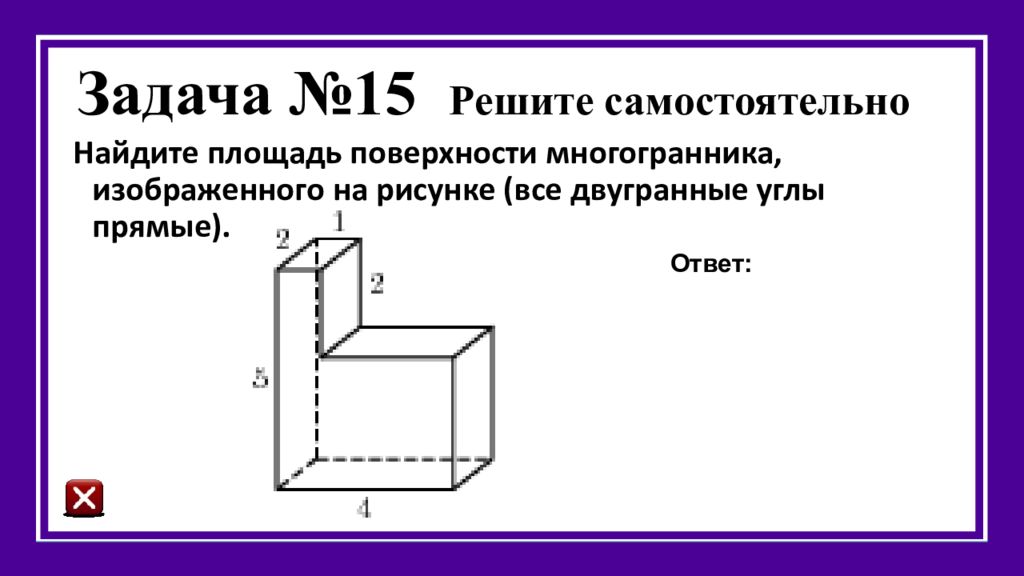
Слайд 34: Задача № 15 Решите самостоятельно
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ:
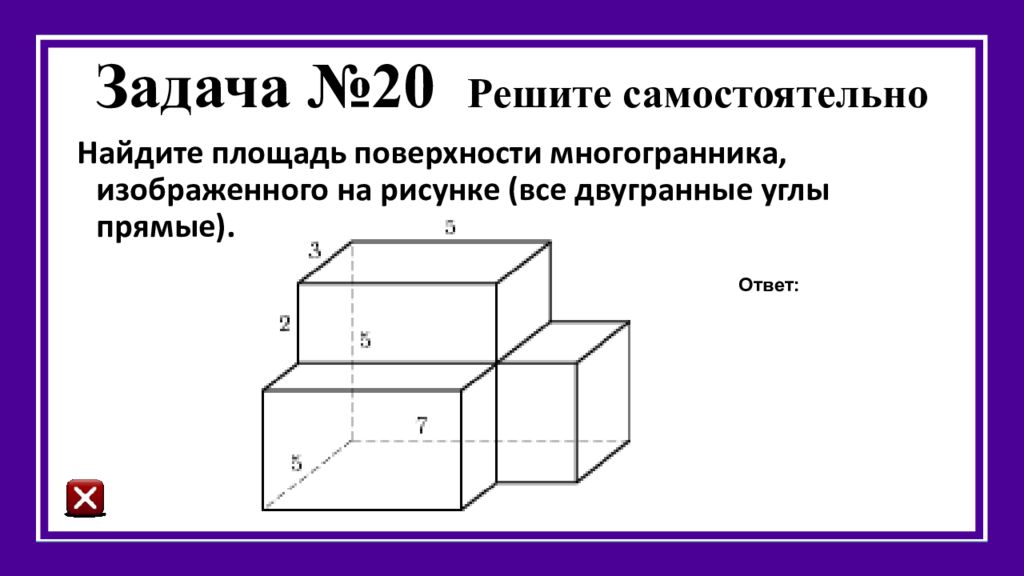
Слайд 35: Задача № 20 Решите самостоятельно
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ:
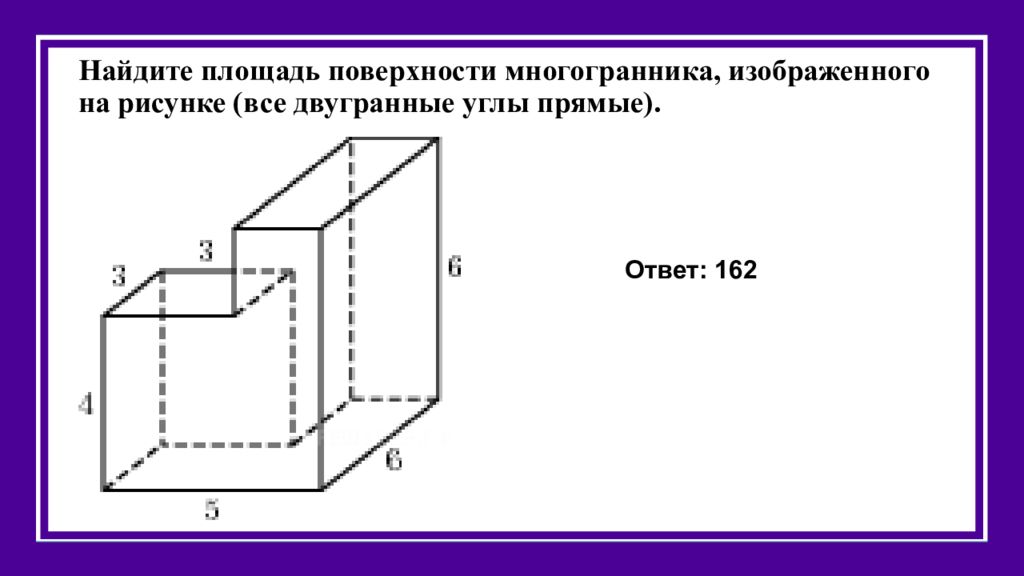
Слайд 36: Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)
Ответ: 162
Слайд 37: Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)
Ответ:
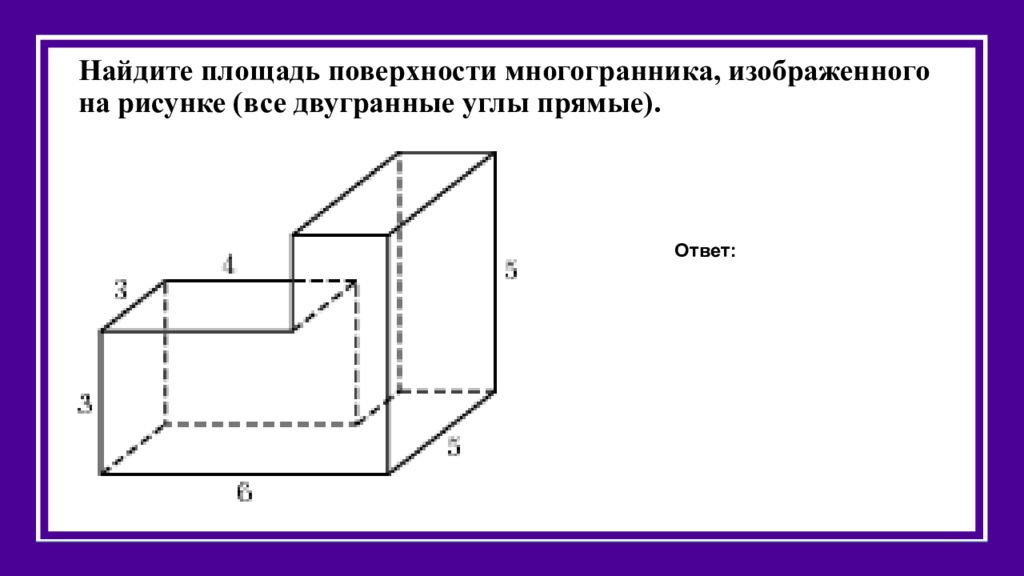
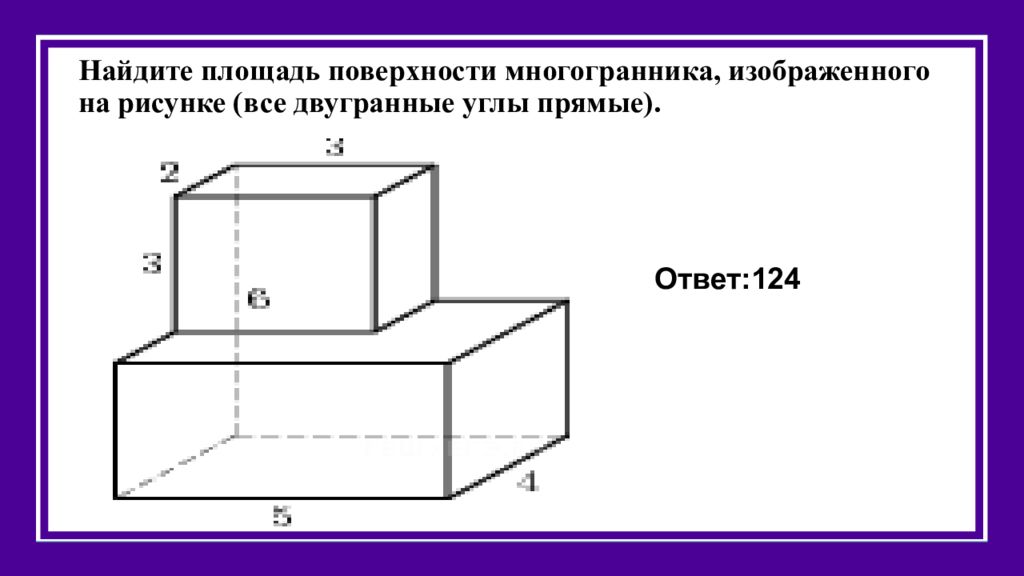
Слайд 38: Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)
Ответ: 124
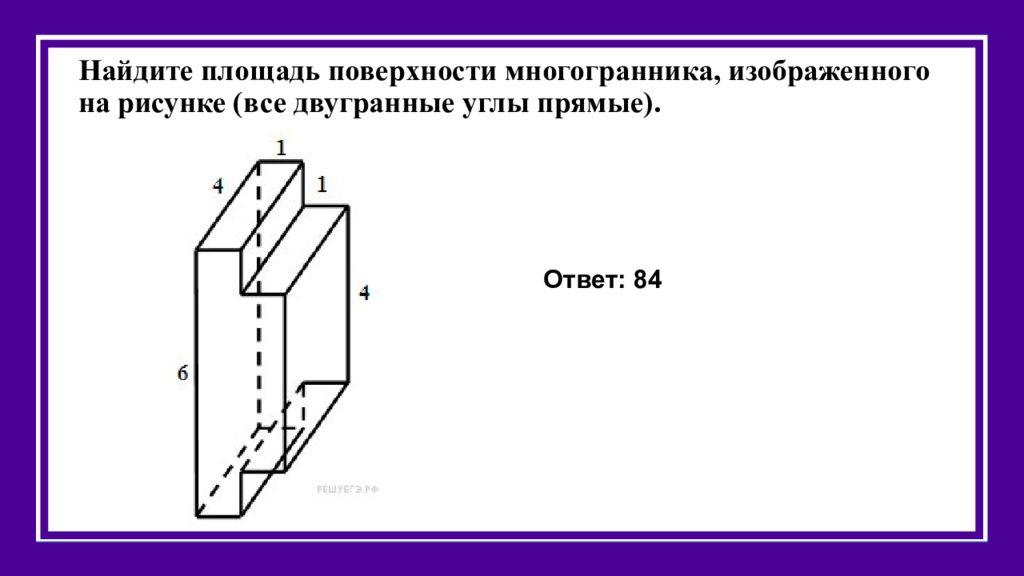
Слайд 39: Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)
Ответ: 84
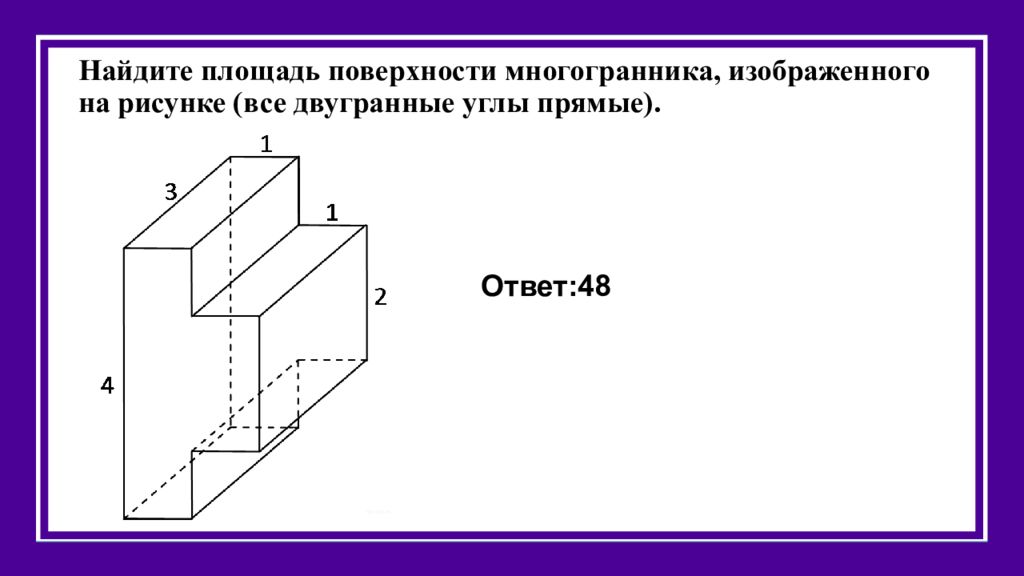
Слайд 40: Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)
Ответ: 48
Последний слайд презентации: Практикум №3 по решению стереометрических задач (базовый уровень): Используемые ресурсы
Шаблон п одготовила учитель русского языка и литературы Тихонова Надежда Андреевна http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg «Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа: http://mathb.reshuege.ru http://lib2.znate.ru/pars_docs/refs/324/323424/323424_html_m22f8f945.gif Автор и источник заимствования неизвестен