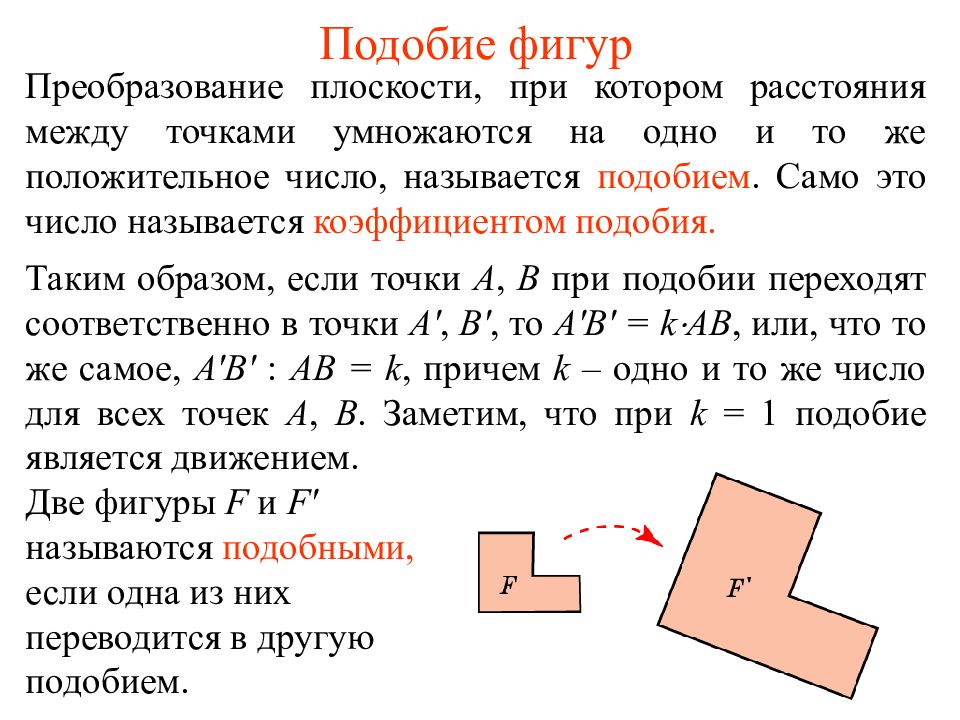
Преобразование плоскости, при котором расстояния между точками умножаются на одно и то же положительное число, называется подобием. Само это число называется коэффициентом подобия. Таким образом, если точки А, В при подобии переходят соответственно в точки A ', B ', то А'В' = k AB, или, что то же самое, A ' B ' : AB = k, причем k – одно и то же число для всех точек А, В. Заметим, что при k = 1 подобие является движением. Две фигуры F и F ' называются подобными, если одна из них переводится в другую подобием.
Свойство 1. Подобие переводит отрезки в отрезки, лучи в лучи и прямые в прямые. Свойство 2. Подобие сохраняет величины углов.
Зафиксируем точку O и положительное число k. Каждой точке A плоскости, отличной от O сопоставим точку A ' на луче OA так, что OA ' = kOA. Точке O сопоставим ее саму. Полученное преобразование плоскости называется гомотетией с центром в точке O и коэффициентом k. Иногда гомотетия рассматривается и с отрицательным коэффициентом k. В этом случае каждой точке A плоскости, отличной от O сопоставляется точка A” на луче противоположном OA так, что OA” = ( –k ) OA.
Докажите, что произведение отрезков любой хорды, проведенной через внутреннюю точку круга, равно произведению отрезков диаметра, проведенного через ту же точку. Решение. Пусть дан круг с центром в точке O, хорда AB и диаметр CD пересекаются в точке E. Докажем, что AE BE = CE DE. Треугольники ACE и DBE подобны. Следовательно, и, значит, AE BE = CE DE.
Какое преобразование плоскости называется подобием? Ответ: Преобразование плоскости, при котором расстояния между точками умножаются на одно и то же положительное число, называется подобием.
Подобны ли равные фигуры? Ответ: Да.
Сформулируйте свойства подобия. Ответ: 1. Подобие переводит отрезки в отрезки, лучи в лучи и прямые в прямые. 2. Подобие сохраняет величины углов.
Какое преобразование плоскости называется гомотетией? Ответ: Гомотетией называется преобразование плоскости, при котором к аждой точке A плоскости, отличной от O сопостав ляется точк а A ' на луче OA так, что OA ' = kOA. Точке O сопостав ляется она сам а.
Фигура F ' подобна фигуре F с коэффициентом k. С каким коэффициентом фигура F подобна фигуре F ' ? Ответ: 1 / k.
Приведите примеры фигур, которые подобны сами себе при любом коэффициенте подобия. Ответ: Прямая, луч, полуплоскость, угол.
Верно ли, что если два угла подобны, то они равны? Ответ: Да.
Как расположены точки A и A ´ относительно центра гомотетии O, если: а) 0 < k < 1; б) k > 1? Ответ: а) A ' лежит между O и A ; б) A лежит между O и A '.
Существуют ли прямые, которые переводятся гомотетией сами в себя? Ответ: Да, прямые, проходящие через центр гомотетии.
Даны точки A, B и гомотетичные им точки A ´, B ´ соответственно. Можно ли найти центр данной гомотетии? Ответ: Да. Это точка пересечения прямых AA’ и BB’.
Как расположены две окружности друг относительно друга, если их центром гомотетии является: а) центр одной из окружностей; б) точка, принадлежащая одной из данных окружностей? Ответ: а) Имеют общий центр; б) касаются внутренним образом.
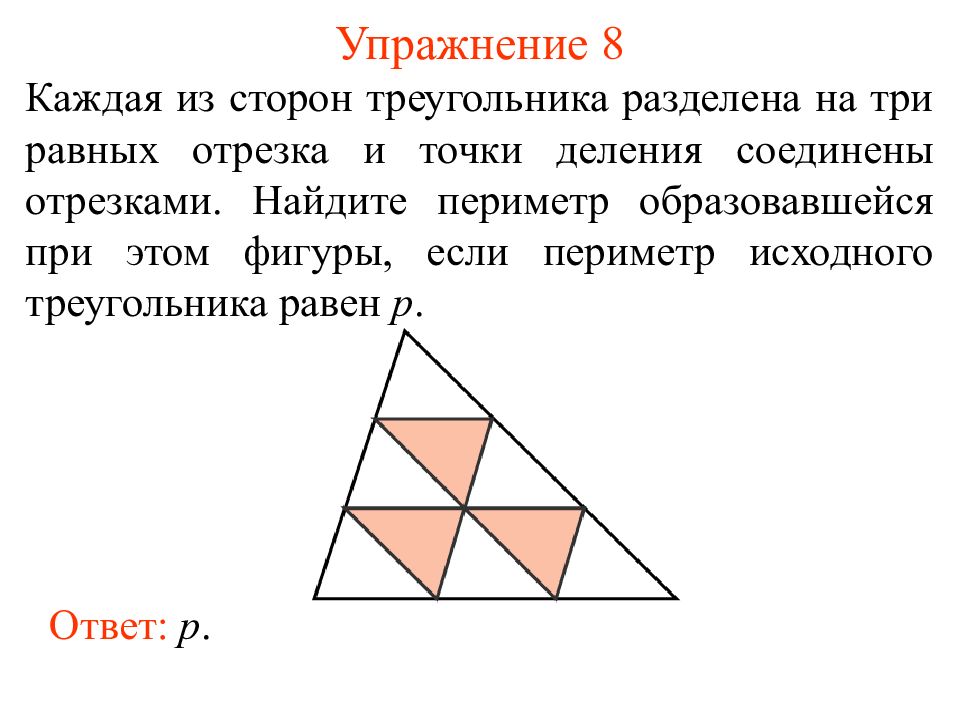
Каждая из сторон треугольника разделена на три равных отрезка и точки деления соединены отрезками. Найдите периметр образовавшейся при этом фигуры, если периметр исходного треугольника равен p. Ответ: p.
Ответ: 2,8 см, 4,2 см, 2 см, 8,4 см. Стороны четырехугольника равны 14 см, 21 см, 10 см и 42 см. Найдите стороны подобного ему четырехугольника, если известно, что его меньшая сторона равна 2 см.
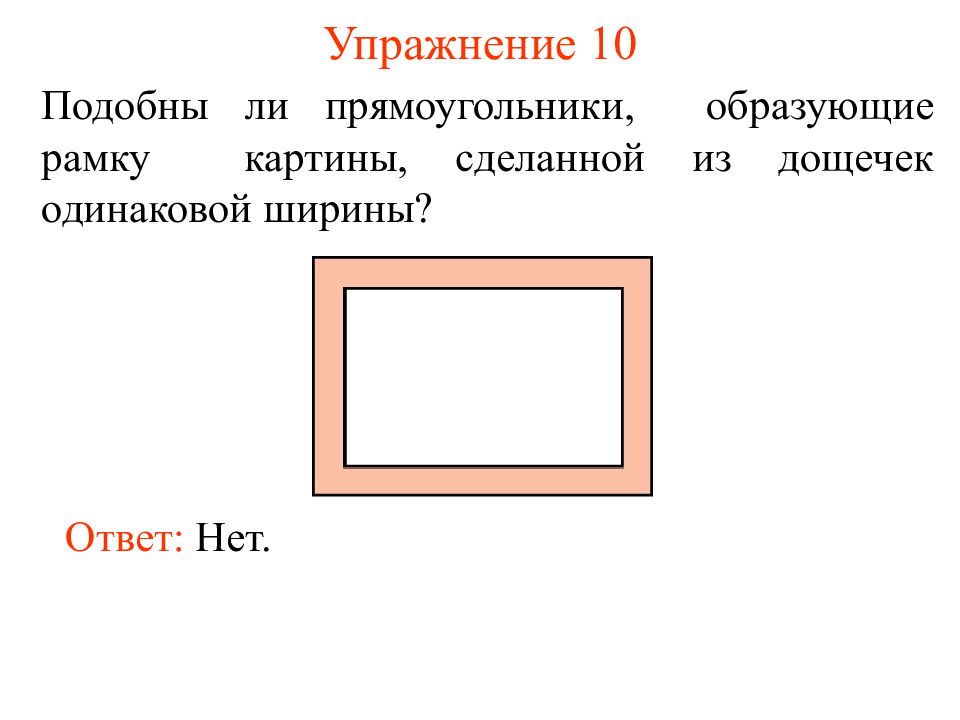
Ответ: Нет. Подобны ли прямоугольники, образующие рамку картины, сделанной из дощечек одинаковой ширины ?
Ответ: Нет. Трапеция разделена средней линией на две трапеции. Будут ли они подобны?
Ответ: а) Равны соответствующие углы; Какие условия должны выполняться, чтобы были подобны: а) два ромба; б) два параллелограмма; в) две равнобедренные трапеции? б) равны соответствующие углы и пропорциональны соответствующие стороны; в) равны соответствующие углы и пропорциональны соответствующие стороны.
На рисунке изображен параллелограмм АВС D со сторонами АВ=а, ВС= b, от которого отсечен другой параллелограмм FBCE, подобный данному. Каким должен быть отрезок BF ? Ответ:
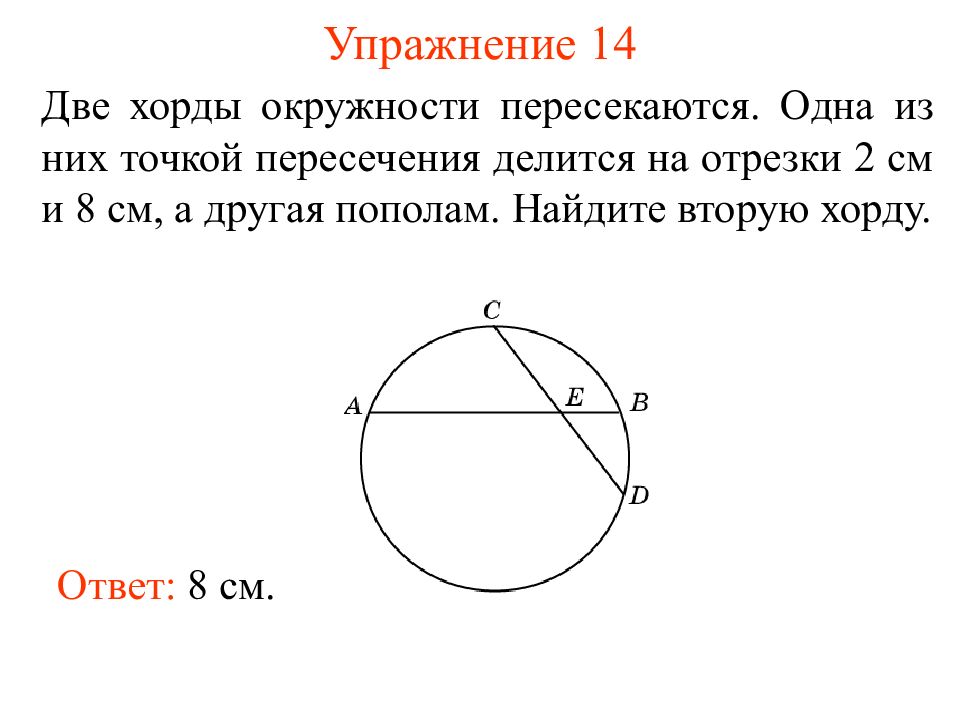
Две хорды окружности пересекаются. Одна из них точкой пересечения делится на отрезки 2 см и 8 см, а другая пополам. Найдите вторую хорду. Ответ: 8 см.
Подобны ли: а) любые две параболы; б) любые два эллипса; в ) любые две гиперболы? Ответ: а) Да; б) нет; в) нет.
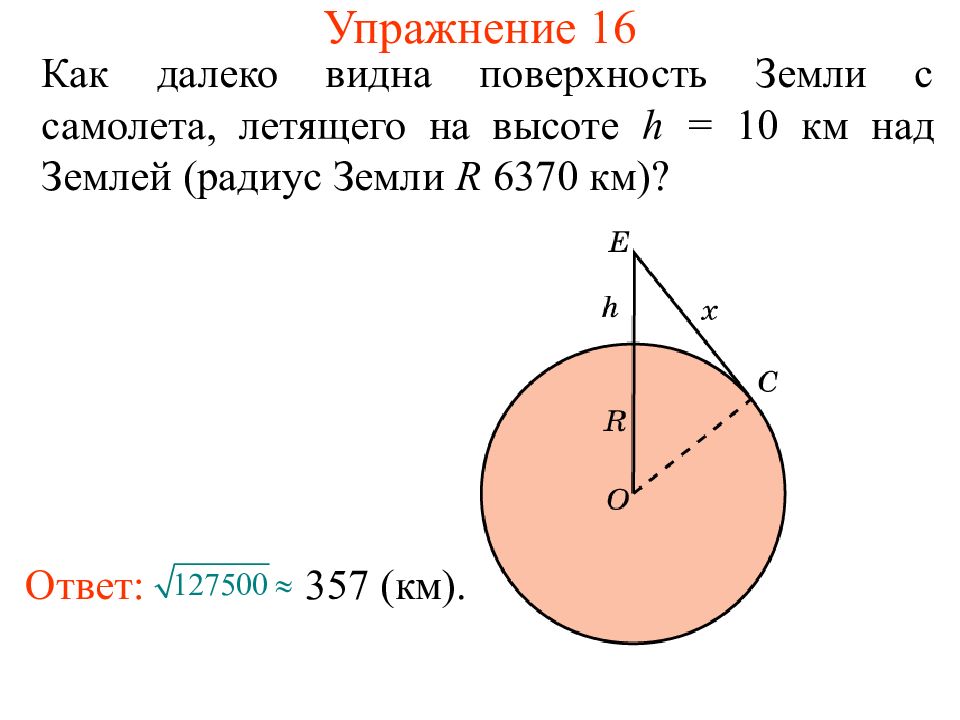
Как далеко видна поверхность Земли с самолета, летящего на высоте h = 10 км над Землей (радиус Земли R 6370 км)? Ответ: 357 (км).
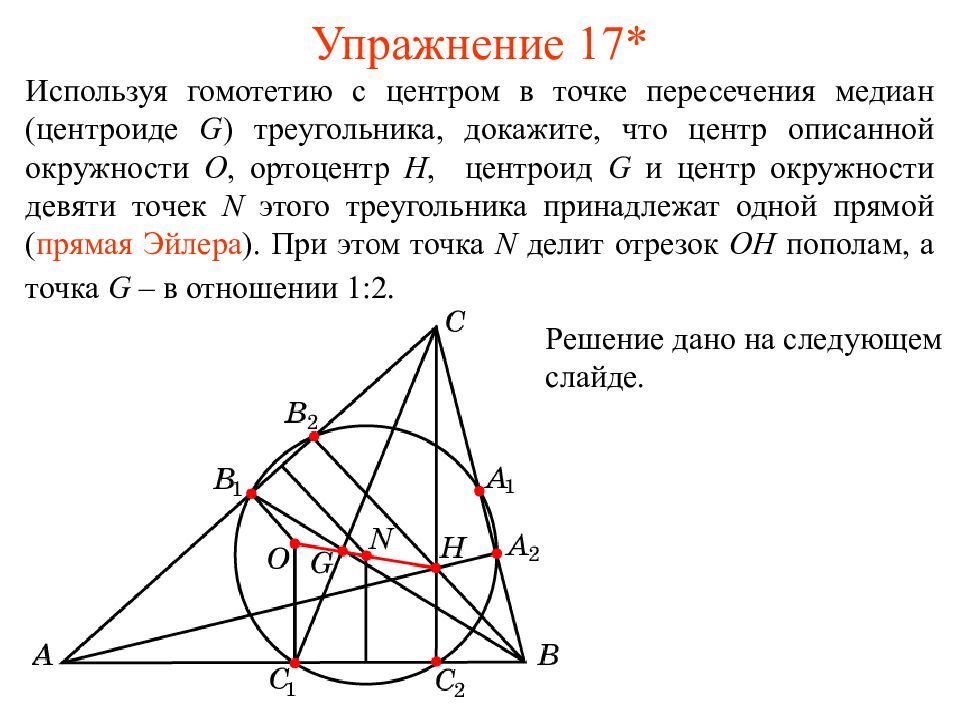
Используя гомотетию с центром в точке пересечения медиан (центроиде G ) треугольника, д окажите, что центр описанной окружности O, ортоцентр H, центроид G и центр окружности девяти точек N этого треугольника принадлежат одной прямой ( прямая Эйлера ). При этом точка N делит отрезок OH пополам, а точка G – в отношении 1:2. Решение дано на следующем слайде.
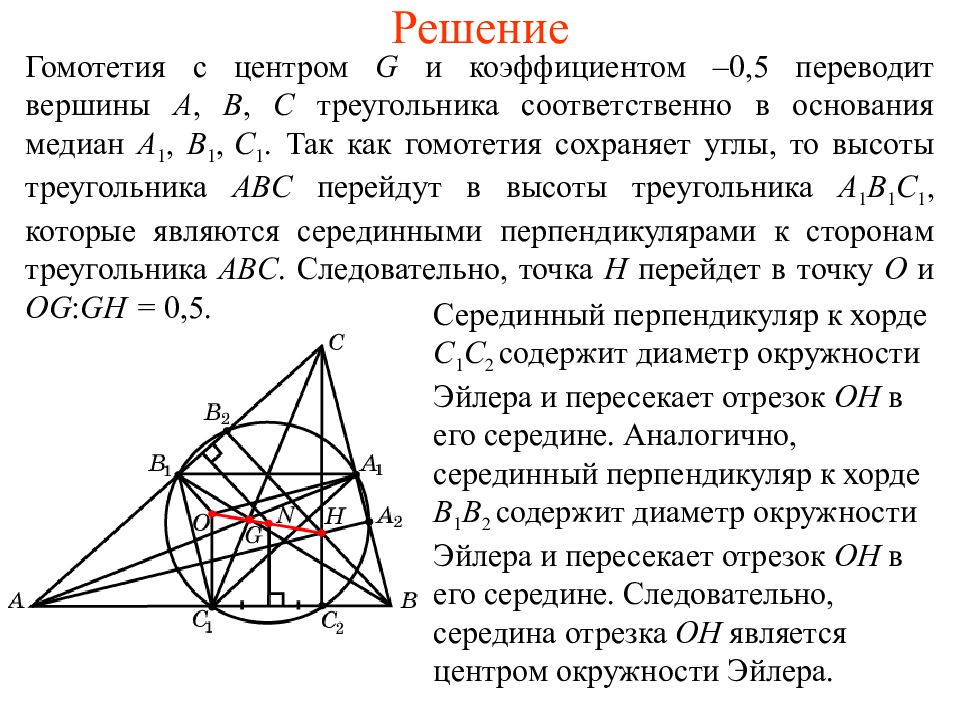
Гомотетия с центром G и коэффициентом –0,5 переводит вершины A, B, C треугольника соответственно в основания медиан A 1, B 1, C 1. Так как гомотетия сохраняет углы, то высоты треугольника ABC перейдут в высоты треугольника A 1 B 1 C 1, которые являются серединными перпендикулярами к сторонам треугольника ABC. Следовательно, точка H перейдет в точку O и OG : GH = 0,5. Серединный перпендикуляр к хорде C 1 C 2 содержит диаметр окружности Эйлера и пересекает отрезок OH в его середине. Аналогично, серединный перпендикуляр к хорде B 1 B 2 содержит диаметр окружности Эйлера и пересекает отрезок OH в его середине. Следовательно, середина отрезка OH является центром окружности Эйлера.
Радиус окружности, описанной около треугольника, равен 1. Найдите радиус окружности Эйлера. Ответ: 0,5.
