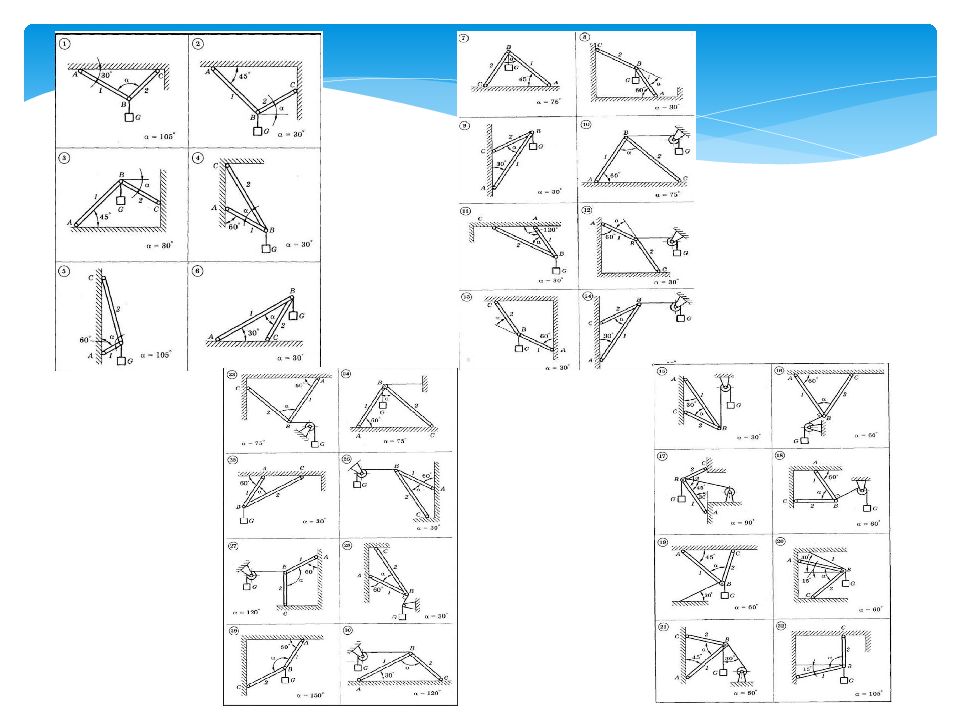
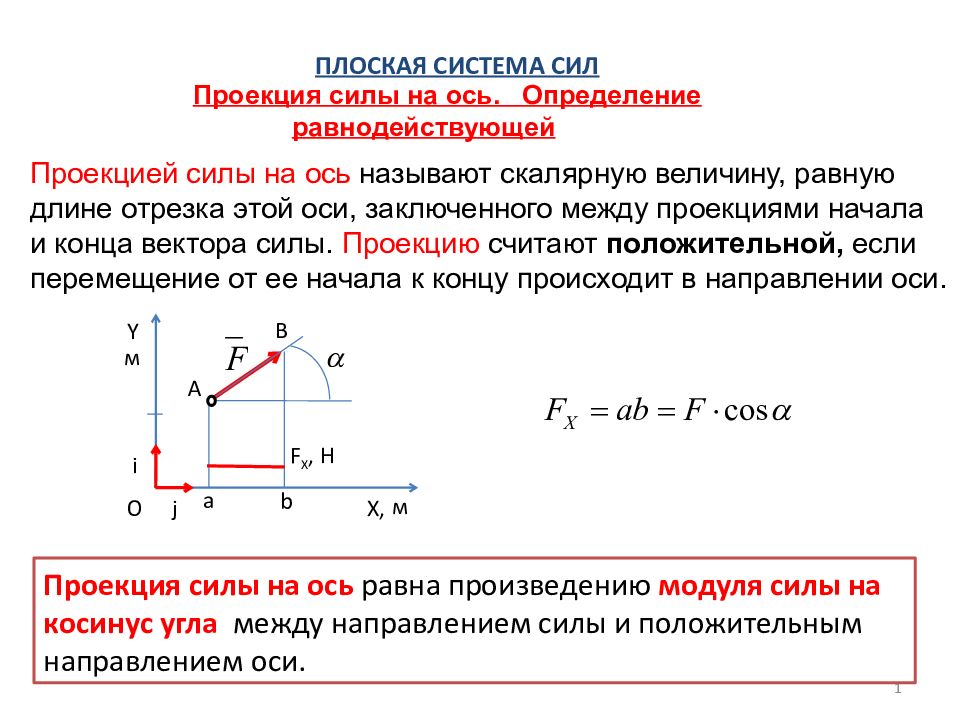
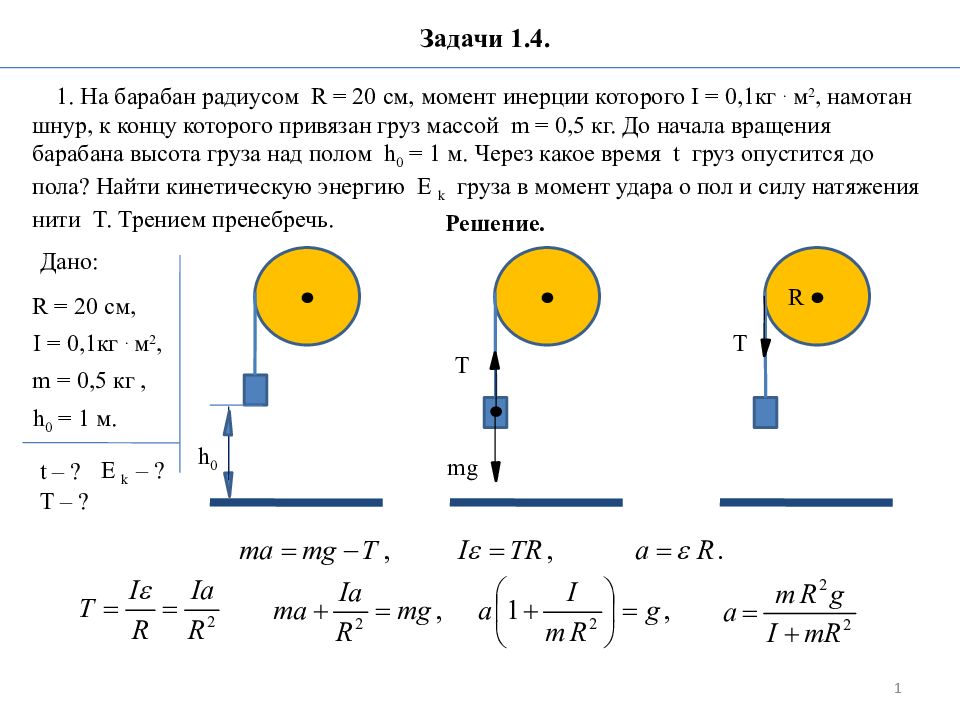
Первый слайд презентации
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ «РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИИ СХОДЯЩЕЙСЯ СИСТЕМЫ СИЛ» ПРЕПОДАВАТЕЛЬ: доцент Бердюгина Ольга Владимировна 2020 год
Слайд 2
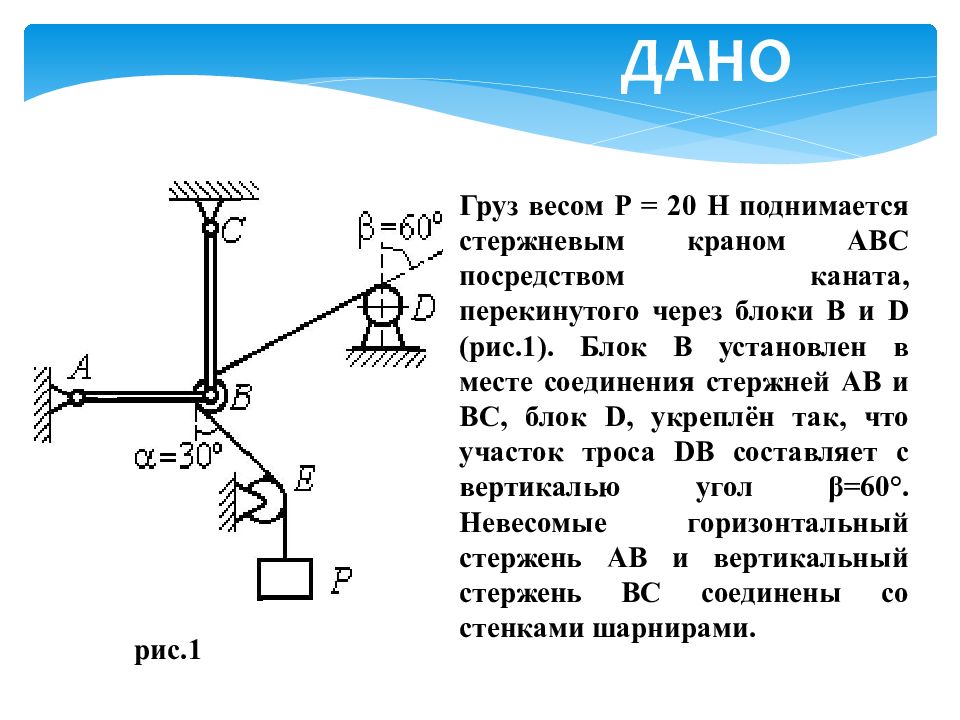
Груз весом Р = 20 Н поднимается стержневым краном АВС посредством каната, перекинутого через блоки В и D (рис.1). Блок В установлен в месте соединения стержней АВ и ВС, блок D, укреплён так, что участок троса DB составляет с вертикалью угол β =60°. Невесомые горизонтальный стержень АВ и вертикальный стержень ВС соединены со стенками шарнирами. рис.1 ДАНО
Слайд 3
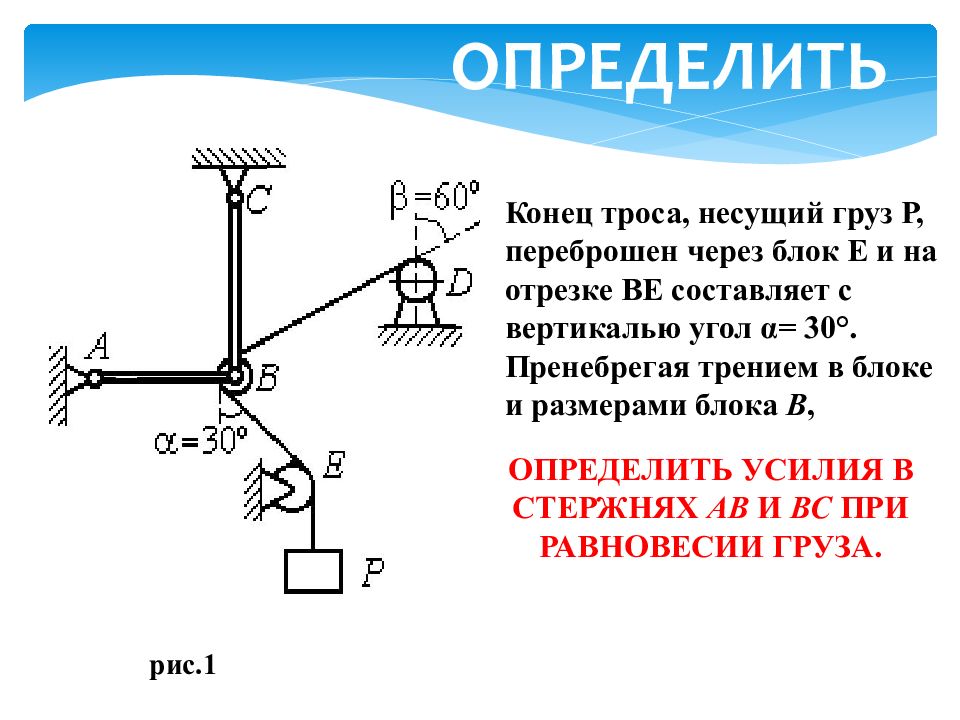
Конец троса, несущий груз Р, переброшен через блок Е и на отрезке BE составляет с вертикалью угол α = 30°. Пренебрегая трением в блоке и размерами блока В, рис.1 ОПРЕДЕЛИТЬ ОПРЕДЕЛИТЬ УСИЛИЯ В СТЕРЖНЯХ АВ И ВС ПРИ РАВНОВЕСИИ ГРУЗА.
Слайд 4
1. Назвать (выделить) объект: тело, узел, равновесие которого надо2. 2. Указать на рисунке силы, действующие на этот объект: а) активные силы; б) назвать каждую связь и пояснить направление реакций связи или их составляющих сил (мысленно освобождая объект от связи на основании аксиомы освобождения от связей); 3. Назвать вид полученной системы сил, учитывая расположение линий действия сил. План ( алгоритм) решения задач статики:
Слайд 5
4. Сформулировать условия равновесия полученной системы сил в алгебраической (координатной) форме. 5. Провести на рисунке координатные оси (если заранее не потребовалось это сделать). 6.Составить уравнения равновесия. 7.Решить систему уравнений с пояснением. 8.Записать ответ.
Слайд 6
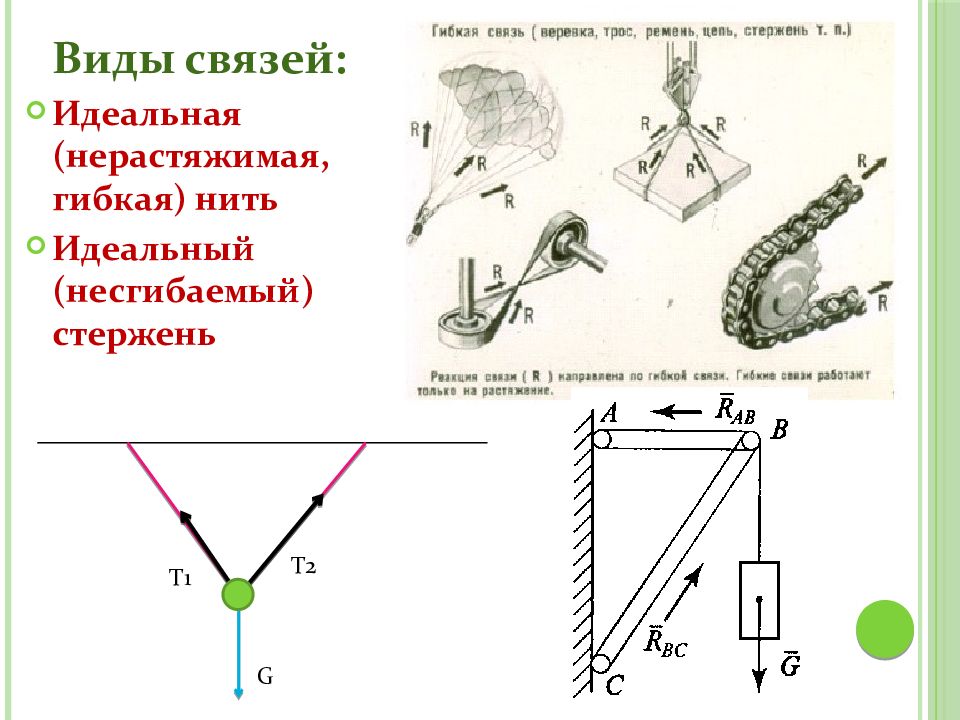
Виды связей: Идеальная (нерастяжимая, гибкая) нить Идеальный (несгибаемый) стержень Т 1 Т 2 G
Слайд 8
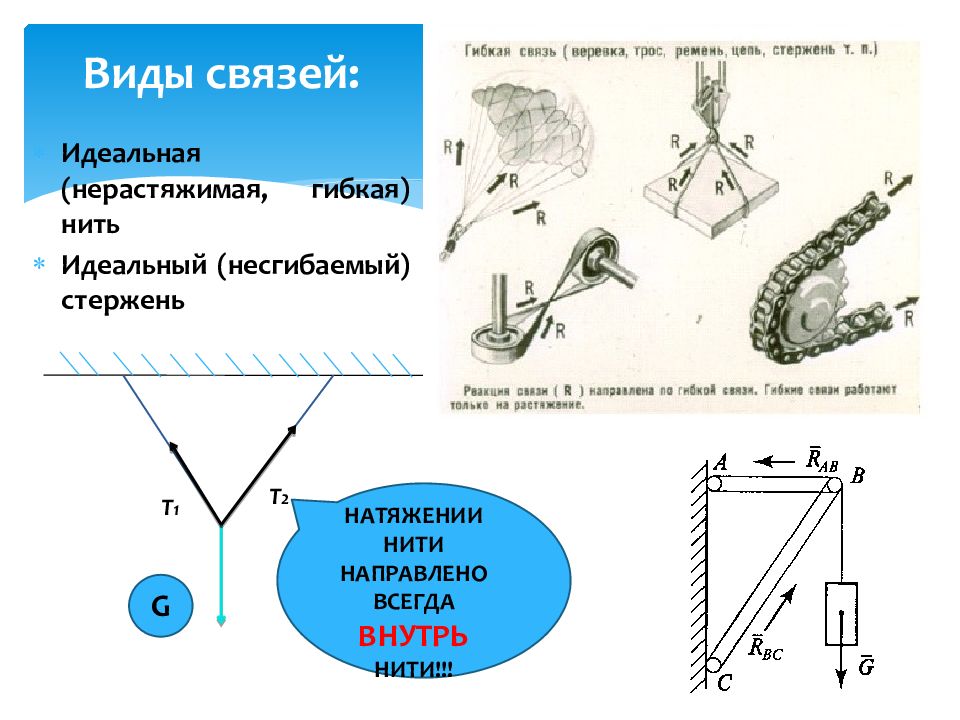
Виды связей: Идеальная (нерастяжимая, гибкая) нить Идеальный (несгибаемый) стержень Т 1 Т 2 G НАТЯЖЕНИИ НИТИ НАПРАВЛЕНО ВСЕГДА ВНУТРЬ НИТИ!!!
Слайд 9
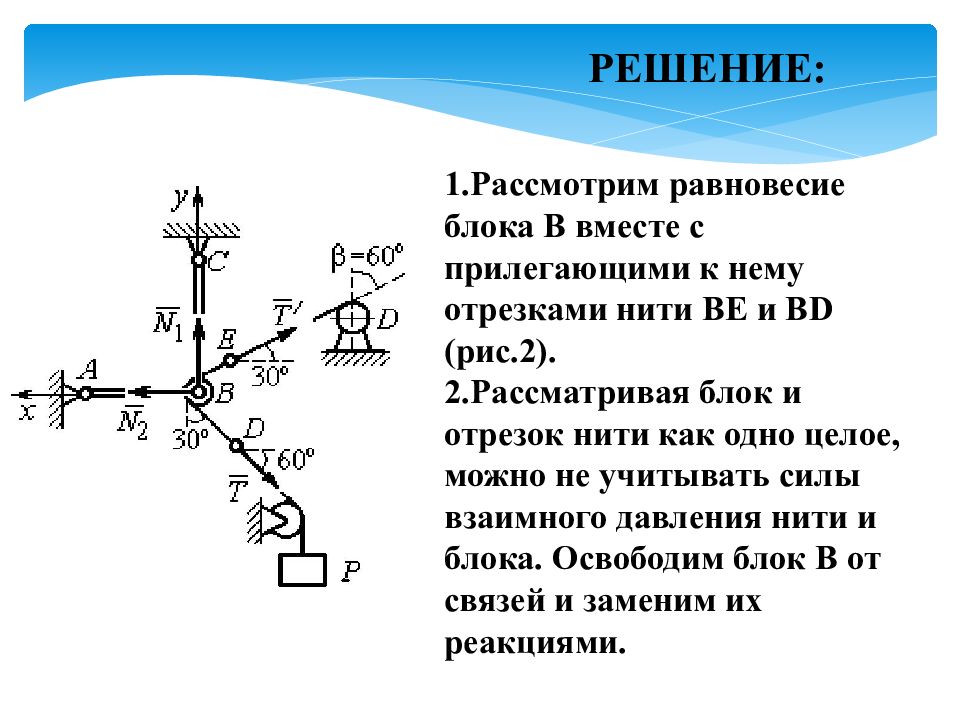
1.Рассмотрим равновесие блока В вместе с прилегающими к нему отрезками нити BE и BD (рис.2). 2.Рассматривая блок и отрезок нити как одно целое, можно не учитывать силы взаимного давления нити и блока. Освободим блок В от связей и заменим их реакциями. РЕШЕНИЕ:
Слайд 10
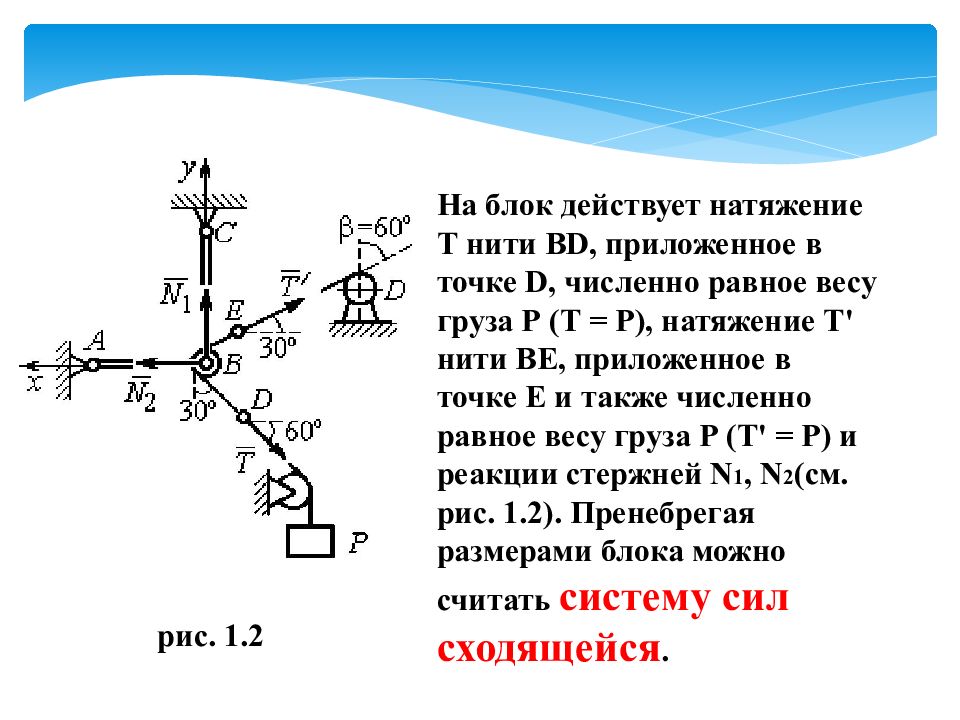
На блок действует натяжение Т нити BD, приложенное в точке D, численно равное весу груза Р (Т = Р), натяжение Т' нити BE, приложенное в точке Е и также численно равное весу груза Р (Т' = Р) и реакции стержней N 1, N 2 (см. рис. 1.2). Пренебрегая размерами блока можно считать систему сил сходящейся. рис. 1.2
Слайд 11
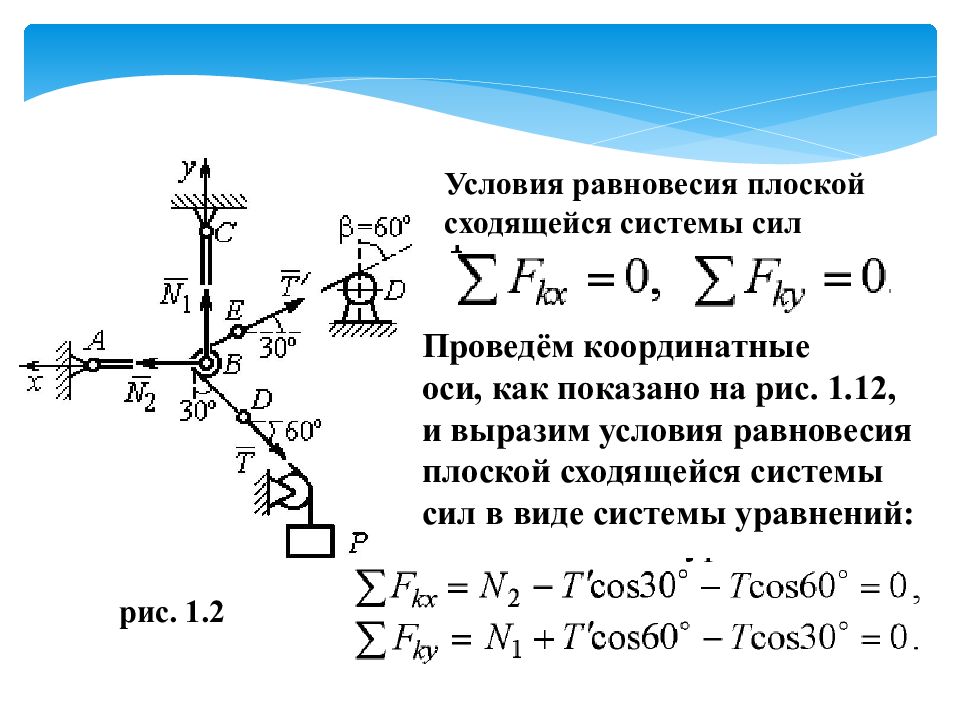
рис. 1.2 Условия равновесия плоской сходящейся системы сил Проведём координатные оси, как показано на рис. 1.12, и выразим условия равновесия плоской сходящейся системы сил в виде системы уравнений:
Слайд 12
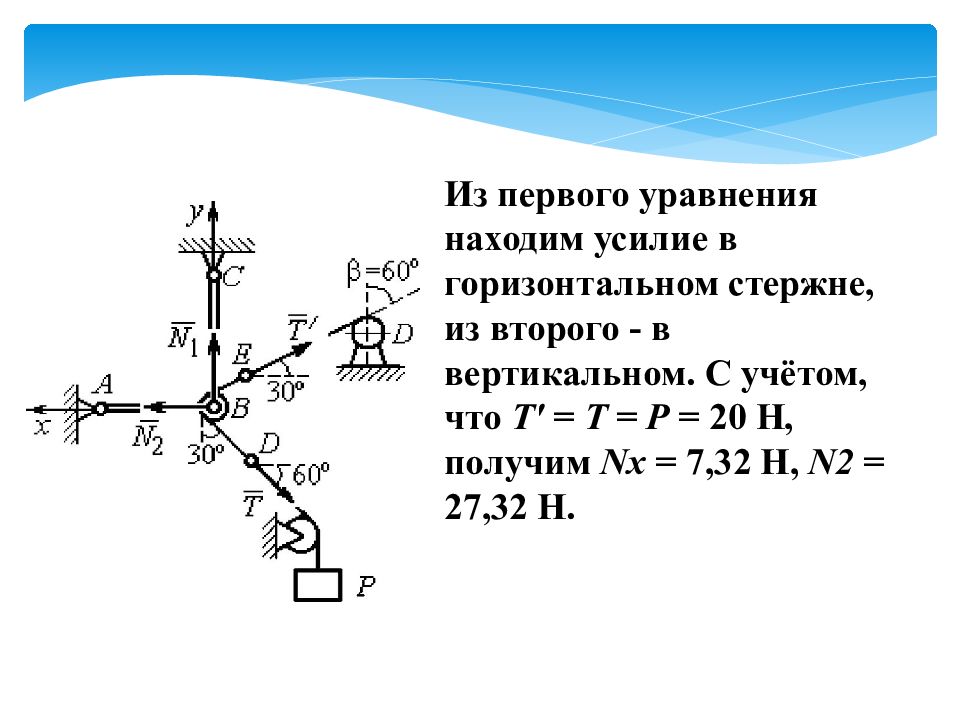
Из первого уравнения находим усилие в горизонтальном стержне, из второго - в вертикальном. С учётом, что Т' = Т = Р = 20 Н, получим Nx = 7,32 Н, N2 = 27,32 Н.