Выполнил: Ученик 9 класса «Б» Шипулин Максим Руководитель: учитель математики Орлова Ольга Васильевна
Актуальность темы : Р ешение задач методами, выходящими за рамки школьной программы. Цель : Научится решать задачи с помощью принципа крайнего и инварианта. Задачи : Изучение принципа крайнего и инварианта. Использование принципа крайнего и инварианта в решении нестандартных задач.
Список литературы Лысенко Ф. Ф., Коновой Е. Г. Принцип крайнего // Математика: подготовка к олимпиадам основные идеи, темы, типы задач. – Ростов – на Дону: Легион, 2018. - С.79 – 96. Принцип крайнего [Электронный ресурс] // URL : http://www.math.md/scho o l/krujok/extremr/extremr.html Принцип крайнего Математика (Олимпиадная математика) [Электронный ресурс] // URL : https://foxford.ru/wiki/matematika/printsip-kraynego
Инвариант – термин, используемый в математике и физике, а также в программировании, обозначает нечто неизменяемое. Задачи называются инвариантом если имеют следующий вид: даны некоторые объекты, над которыми разрешается выполнять определенные операции. Одним из инвариантов является принцип крайнего. Задачи решаются следующим способом: рассматривается какой-нибудь « крайний », « граничный », « экстремальный » элемент, то есть элемент, при котором некоторая величина принимает наибольшее или наименьшее значение, например, наибольшую сторону треугольника, наибольшее или наименьшее расстояние и т. д. К этому же методу иногда относят задачи, где приходится упорядочивать ряд чисел по возрастанию (убыванию) или находить асимптоты. Одним из случаев принципа крайнего является метод экстремального контр примера: предполагаем, что утверждение задачи неверно. Тогда существует «экстремальный» в некотором смысле контр пример. Если же выяснится, что его можно ещё уменьшить или увеличить, то получится необходимое противоречие. Доказательства становятся более понятнее, если переформулировать ее с использованием логически эквивалентной концепции минимального контр примера.
Разменный автомат меняет одну монету на пять других. Можно ли с его помощью разменять одну монету на 27 монет?
Решение. После каждого такого размена количество монет увеличивается на 4, при этом остаток при делении на 4 у числа монет остаётся неизменным. Сначала у нас была 1 монета, значит, остаток всегда будет 1. У числа 27 при делении на 4 остаток 3, таким образом нельзя разменять одну монету на 27 монет.
В вершинах куба стоят числа, среди которых есть 0 и 1. На каждом шаге все числа заменяются на среднее арифметическое чисел, стоящих в вершинах, соединённых ребром данной вершиной. Через 10 таких шагов во всех вершинах числа оказались равны исходным. Найти, какими могли быть исходные числа. Задача 2
Решение. Пусть M i – максимальное число на данном шаге, а m i – минимальное. Тогда выполняется следующие соотношение: M 0 > M 1 > … > M 10. Так как после десятого шага числа оказались равны исходным, то M 0 = M 1 = … = M 10 = M. Аналогично m 0 = m 1 = … = m 10 = m. Занумеруем вершины куба так, чтобы рёбра соединяли числа разной чётности (рис.1). Пусть в первой вершине после десятого шага стоит максимальное число, тогда после девятого шага в вершинах, соседних с 1 (вершины 2, 6, 4), были числа, равные максимальному. После восьмого шага должны были быть равны максимальному числа во всех вершинах с нечётными номерами. Аналогично можно получить, что все исходные числа, стоящие в вершинах одинаковой чётности, равны. По условию, среди исходных чисел были 0 и 1. Таким образом, возможны две исходные расстановки: В чётных вершинах единицы, в нечётных – нули; В чётных вершинах нули, в нечётных – единицы.
У гнома есть чашечные весы без гирь и 8 алмазов. Он хочет знать, верно ли, что два алмаза всегда тяжелее одного. Как ему гарантированно проверить это а) за 19 взвешиваний; б) за 13 взвешиваний?
Решение. Чтобы проверить это, необходимо и достаточно сравнить вес самого тяжёлого и двух самых легких алмазов. а) Чтобы узнать, какой из восьми алмазов самый тяжёлый, достаточно 7 взвешиваний. За ещё 6 взвешиваний мы найдем самый легкий алмаз, и ещё за 5 мы найдем самый легкий среди оставшихся шести алмазов. Теперь мы знаем два самых легких и самый тяжелый алмаз и последним взвешиванием сравниваем их. Всего нужно 7+6+5+1=19 взвешиваний. б) Разобьём алмазы на 4 пары и найдем более тяжелый в каждой паре. Из каждой пары возьмем более легкий алмаз. Эти 4 алмаза снова разобьем на две пары. Найдем наиболее легкий алмаз в каждой из двух пар, а затем сравним эти два найденных алмаза. Таким образом мы найдем самый легкий алмаз среди всех. Занумеруем алмазы числами от 1 до 8 так, чтобы последнее взвешивание показало m 1 < m 5, два проведенных до того взвешивания показали m 1 < m 3 и m 5 < m 7, а при самом первом разбиении было m 1 < m 2, m 3 < m 4, m 5 < m 6, m 7 < m 8. Самый легкий алмаз уже найден. Найден второй по легкости алмаз. Кандидатами на эту роль являются m 2, m 3 и m 5. Двух взвешиваний достаточно, чтобы определить легчайший алмаз из этой тройки. Теперь нужно найти самый тяжелый алмаз. Кандидатами являются m 2, m 4, m 6 и m 8. Самый тяжелый среди них можно найти за 3 взвешивания. Уже было использовано 4+3+2+3 = 12 взвешиваний. Последним 13 взвешиванием мы кладем на одну чашу самый тяжелый алмаз, а на другую – два наиболее легких.
На кольцевом треке 10 велосипедистов стартовали одновременно из одной точки и поехали с различными постоянными скоростями в одну сторону. Если после старта велосипедисты оказываются одновременно в одной точке, назовём это встречей. До полудня каждые два велосипедиста встретились хотя бы один раз, при этом никакие три не встретились одновременно. Докажите, что до полудня у каждого велосипедиста было не менее 25 встреч.
Решение. Пусть S – длина трека, u 1 < u 2 < … < u 10 – скорости велосипедистов, u = min ( u 2 – u 1, u 3 – u 2, …, u 10 – u 9 ). Велосипедисты с номерами i, j ( i < j ) встречаются через время. Самый большой из таких промежутков равен, и для того чтобы встретились каждые два велосипедиста, нам необходимо ждать не меньше этого промежутка. Поскольку u 1 – u 2 > ( j – i ) u, то за это время велосипедисты с номерами i, j встретятся не менее ( j – i ) раз. Таким образом, суммарное количество встреч велосипедиста с номером k не меньше суммы и Минимальное количество встреч, равное 25, получаем для велосипедистов с номерами 5 и 6.
В железнодорожной системе некоторой страны с любой станции можно проехать на любую (возможно, с пересадками ). Доказать, что можно так выбрать станцию и закрыть её на ремонт (без права проезда через неё), что по – прежнему можно будет проехать с любой оставшейся на любую оставшуюся.
Решение. Очевидно, что если можно найти станцию, из которой выходит только один путь, то её можно закрыть на ремонт. Если такой станции нет, то перекроем наибольшее количество путей так, чтобы от любой станции всё равно можно было добраться до любой другой. Понятно, что после этого не будет ни одного замкнутого маршрута. Покажем, что теперь можно найти станцию, из которой выходит ровно один тоннель. Начнем с любой станции будем перемещаться по путям так, чтобы не возвращаться на ту же станцию, с которой только что пришли. Мы не сможем попасть на одну станцию дважды, иначе получился бы замкнутый маршрут. Значит, дойдя до определённой станции, мы не сможем продолжить маршрут, и это означает, что из неё выходит один путь. Станцию на конце этого пути можно закрыть на ремонт.
В некотором районе, состоящем из нескольких деревень, число женихов равно числу невест. Известно, что в каждой из деревень общее число женихов и невест не превосходит половины от общего числа женихов и невест всего района. Доказать, что всех этих молодых людей можно поженить так, что в каждой паре муж и жена будут из разных деревень.
Решение. Возьмём деревню, в которой больше всего женихов и невест ( N человек). Во – первых, мы можем составить пару, в которой один из поженившихся будет из этой деревни (так как в других деревнях тоже хоть кто – то есть, а всего женихов и невест поровну). Во – вторых, если мы эту пару зафиксируем и уберём данных жениха и невесту из рассмотрения, то условие задачи сохранится. Действительно, общее число людей было не менее 2 N, в каждой деревне их не больше, чем N, есть три варианта: Число людей 2 N и есть другая деревня с N людьми. Тогда мы взяли по 1 человеку из каждой, и в них осталось поровну; Число людей больше чем 2 N. Тогда мы взяли двух человек и осталось хотя бы 2 N, а в деревнях не больше чем по N ; Людей 2 N и нет других деревень с N людьми. Тогда осталось (2 N -2) человек и не более чем по ( N -1) в каждой из деревень. В любом случае условие задачи сохранилось, а число не поженившихся людей уменьшилось. Значит, действуя таким образом, мы сможем уменьшать число не поженившихся до нуля.
На плоскости дано m точек, не лежащих на одной прямой. Доказать, что можно найти ломаную линию без пересечений с вершинами в этих точках.
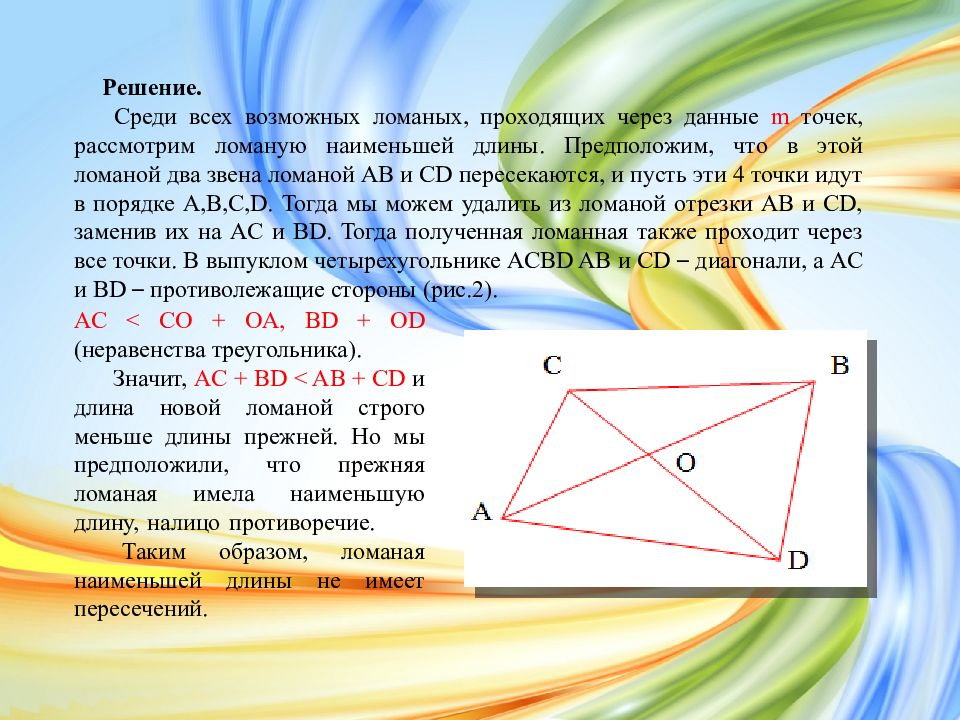
Решение. Среди всех возможных ломаных, проходящих через данные m точек, рассмотрим ломаную наименьшей длины. Предположим, что в этой ломаной два звена ломаной AB и CD пересекаются, и пусть эти 4 точки идут в порядке A, B, C, D. Тогда мы можем удалить из ломаной отрезки AB и CD, заменив их на AC и BD. Тогда полученная ломанная также проходит через все точки. В выпуклом четырехугольнике ACBD AB и CD – диагонали, а AC и BD – противолежащие стороны (рис.2). AC < CO + OA, BD + OD (неравенства треугольника). Значит, AC + BD < AB + CD и длина новой ломаной строго меньше длины прежней. Но мы предположили, что прежняя ломаная имела наименьшую длину, налицо противоречие. Таким образом, ломаная наименьшей длины не имеет пересечений.
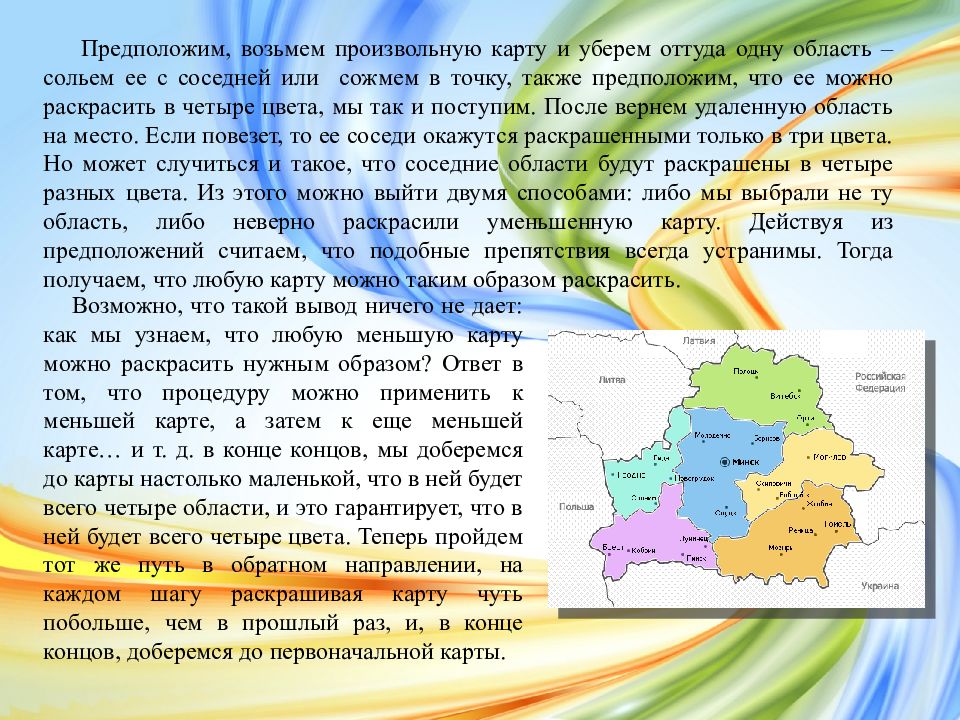
Предположим, возьмем произвольную карту и уберем оттуда одну область – сольем ее с соседней или сожмем в точку, также предположим, что ее можно раскрасить в четыре цвета, мы так и поступим. После вернем удаленную область на место. Если повезет, то ее соседи окажутся раскрашенными только в три цвета. Но может случиться и такое, что соседние области будут раскрашены в четыре разных цвета. Из этого можно выйти двумя способами: либо мы выбрали не ту область, либо неверно раскрасили уменьшенную карту. Действуя из предположений считаем, что подобные препятствия всегда устранимы. Тогда получаем, что любую карту можно таким образом раскрасить. Возможно, что такой вывод ничего не дает: как мы узнаем, что любую меньшую карту можно раскрасить нужным образом? Ответ в том, что процедуру можно применить к меньшей карте, а затем к еще меньшей карте… и т. д. в конце концов, мы доберемся до карты настолько маленькой, что в ней будет всего четыре области, и это гарантирует, что в ней будет всего четыре цвета. Теперь пройдем тот же путь в обратном направлении, на каждом шагу раскрашивая карту чуть побольше, чем в прошлый раз, и, в конце концов, доберемся до первоначальной карты.
