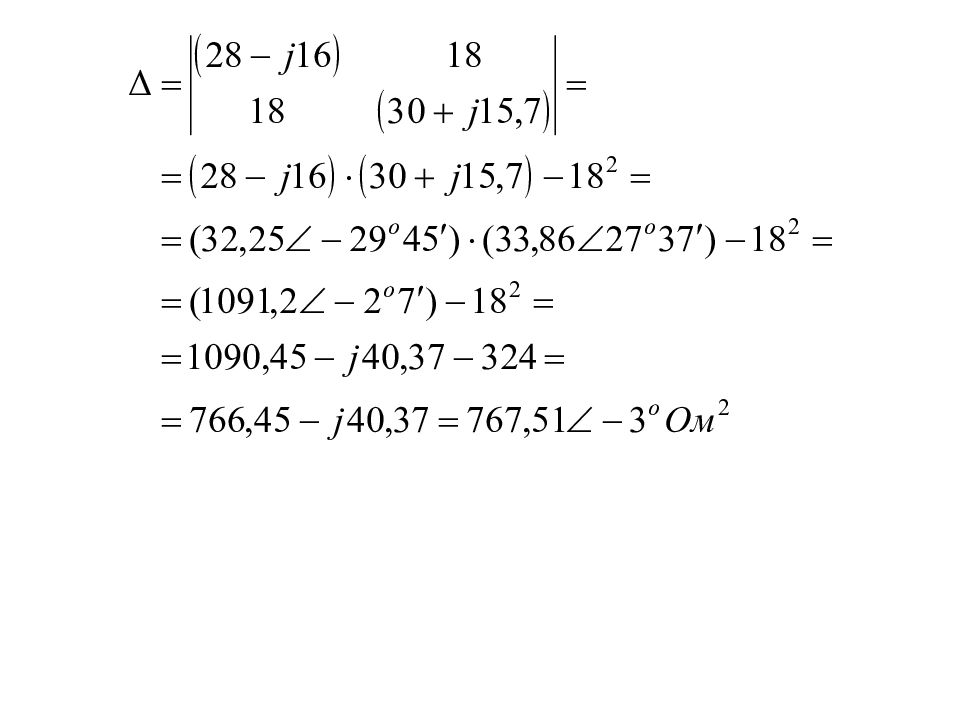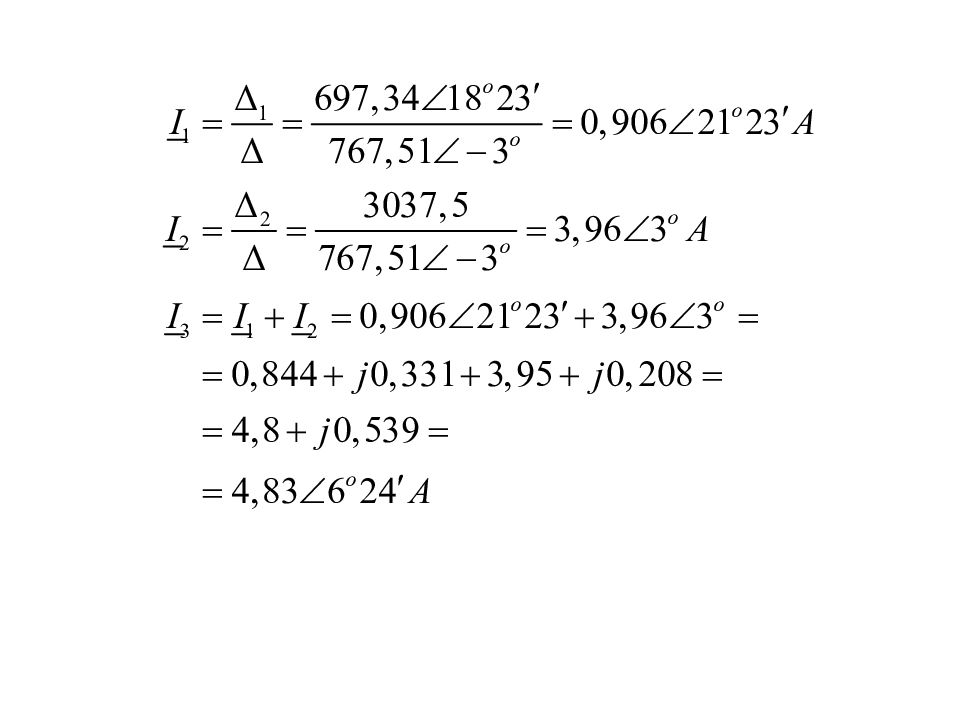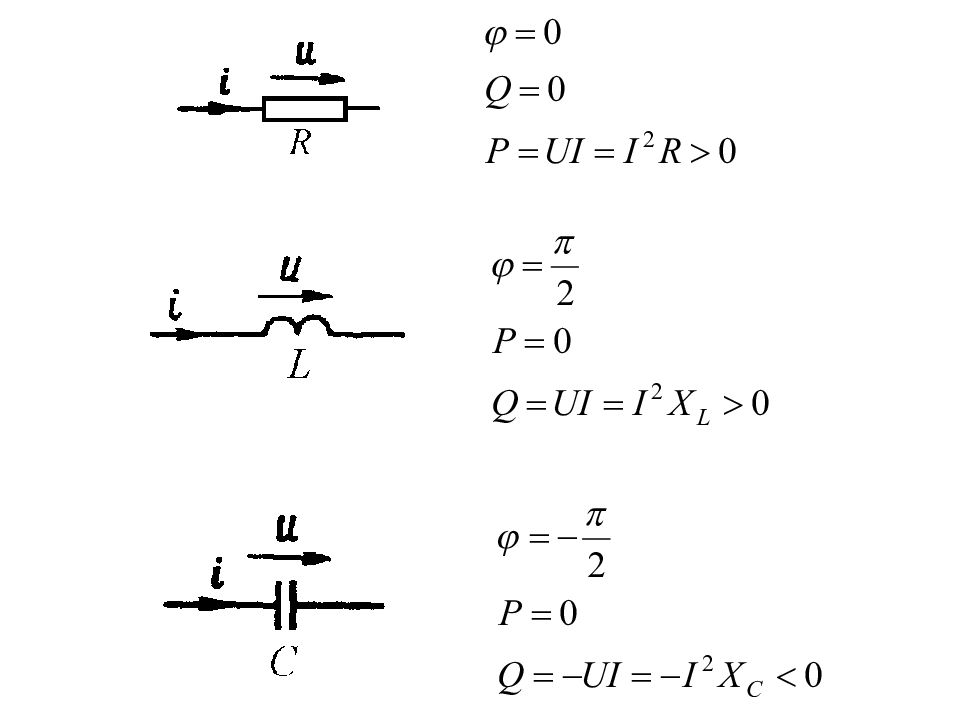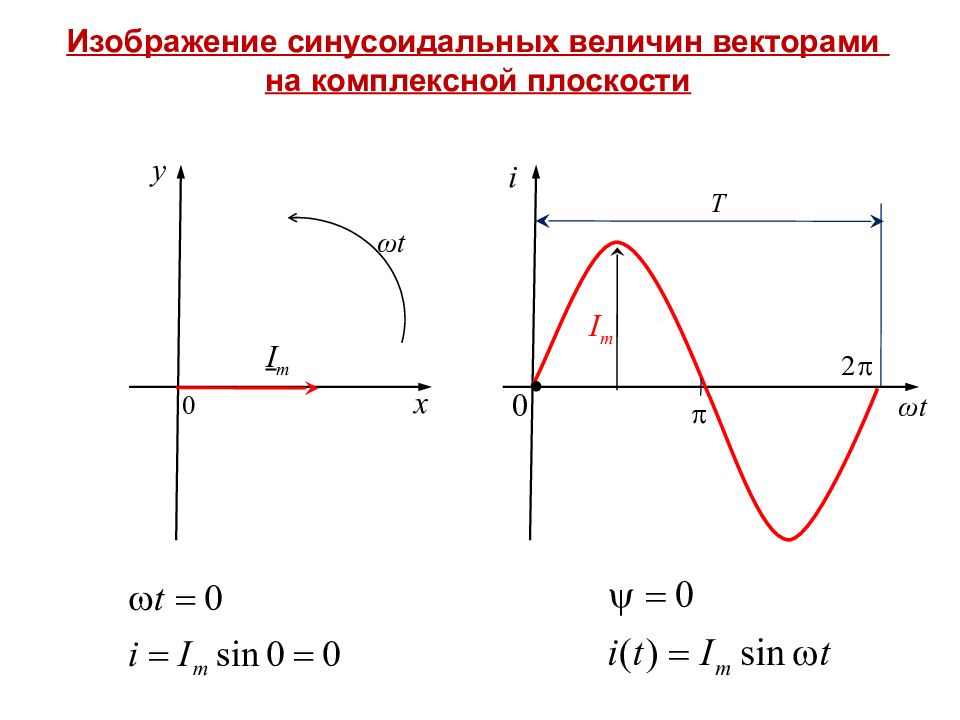
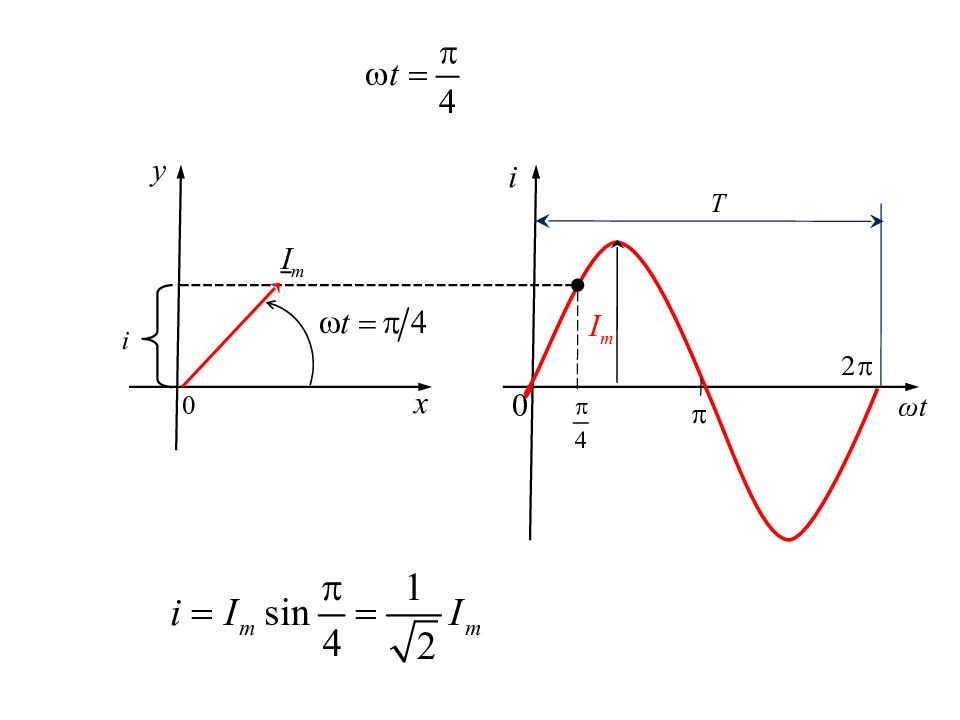
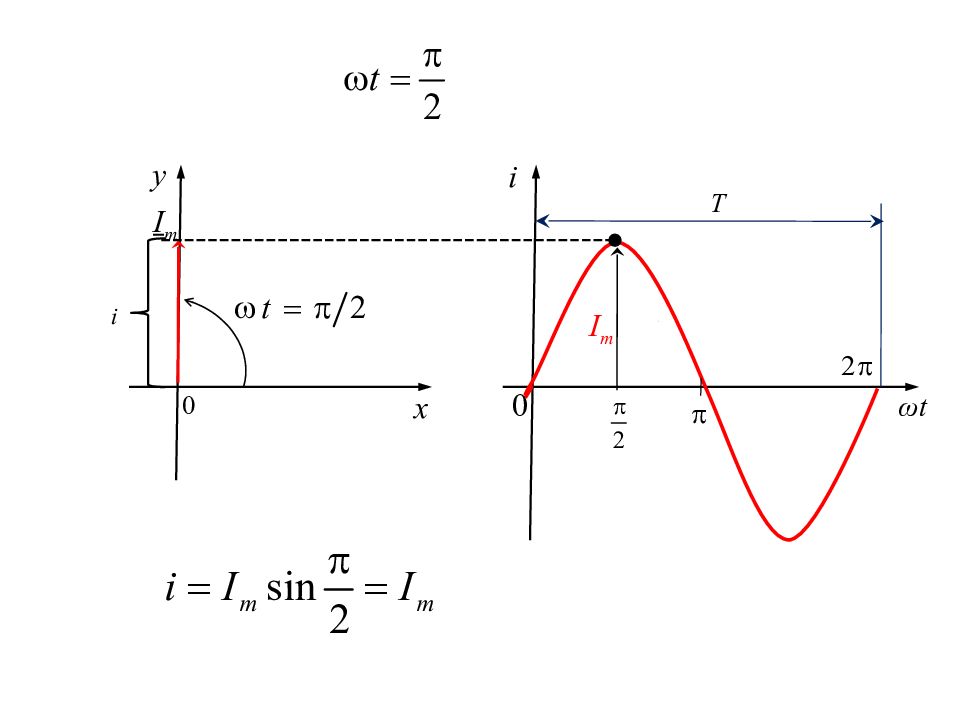
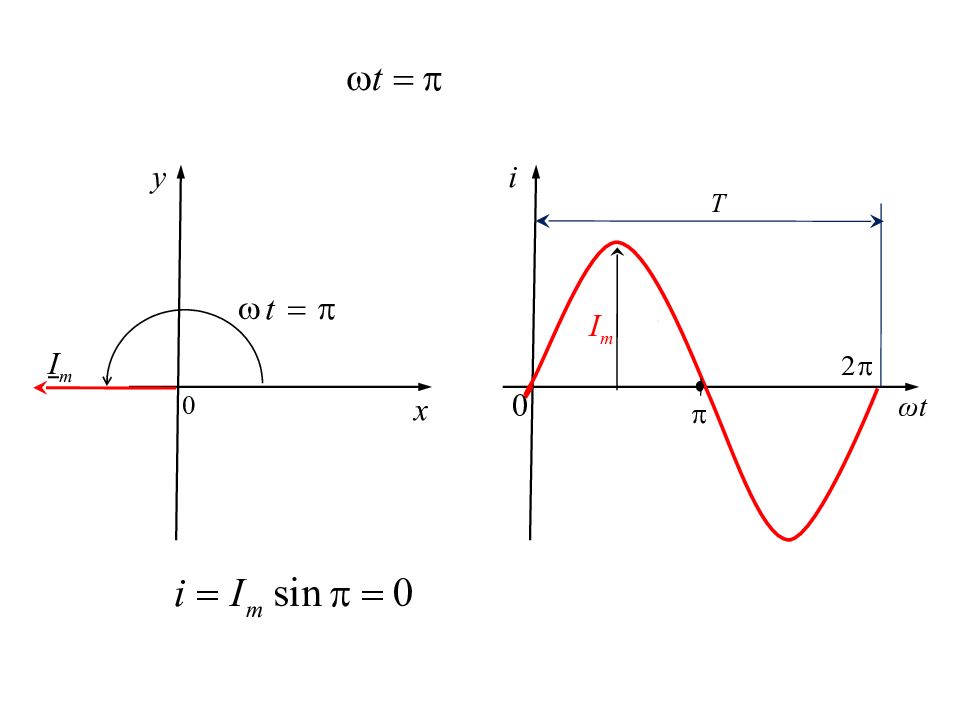
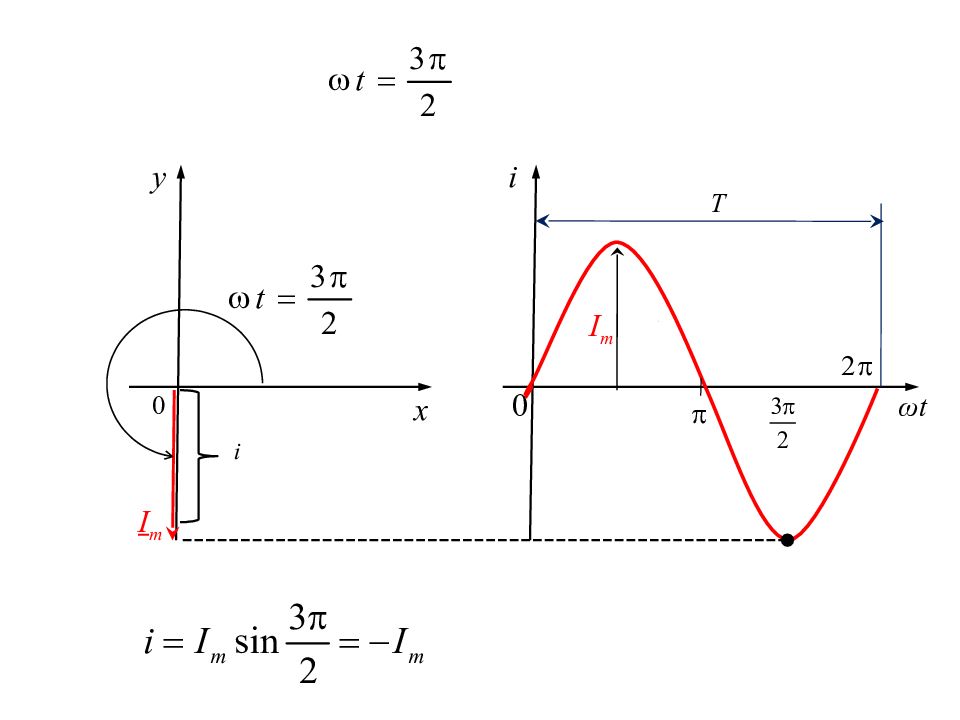
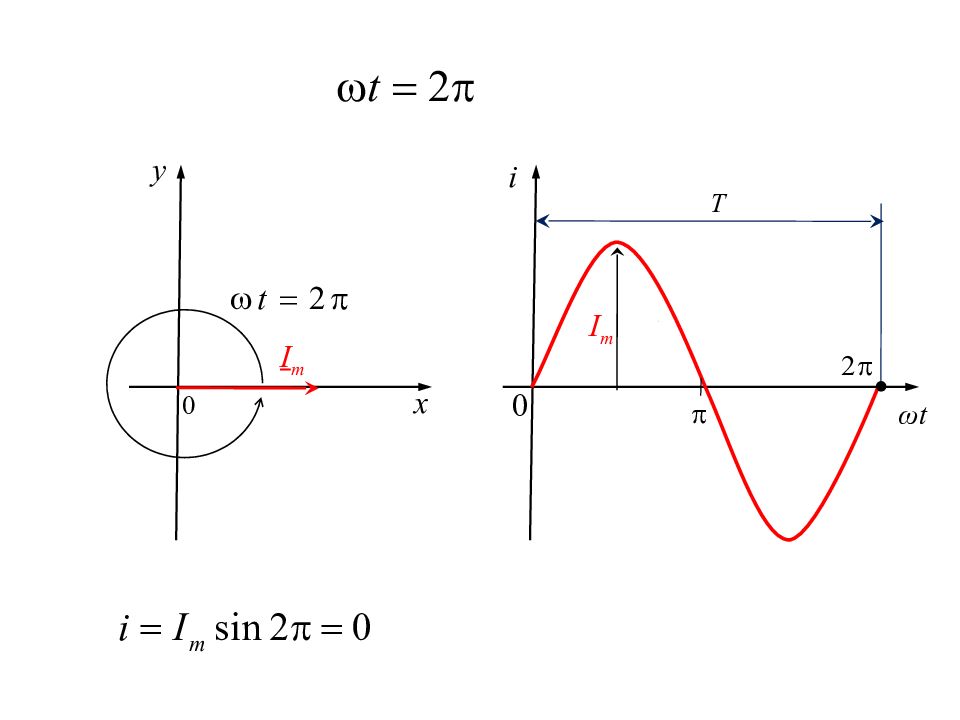
Изображение синусоидальных величин векторами на комплексной плоскости i ω t Т I m I m ω t 0 0 x y
i ω t Т I m I m i 0 0 x y
i ω t Т I m I m i 0 0 x y
i ω t Т I m I m 0 0 x y
i ω t Т I m I m 0 0 x y i
i ω t Т I m I m 0 0 x y
i(t) u(t) r 1. e(t) C. i(t) u(t) 0 I m U m
Поскольку взаимное расположение векторов со временем не меняется, то векторы можно не вращать, а показывать их на момент времени t =0.
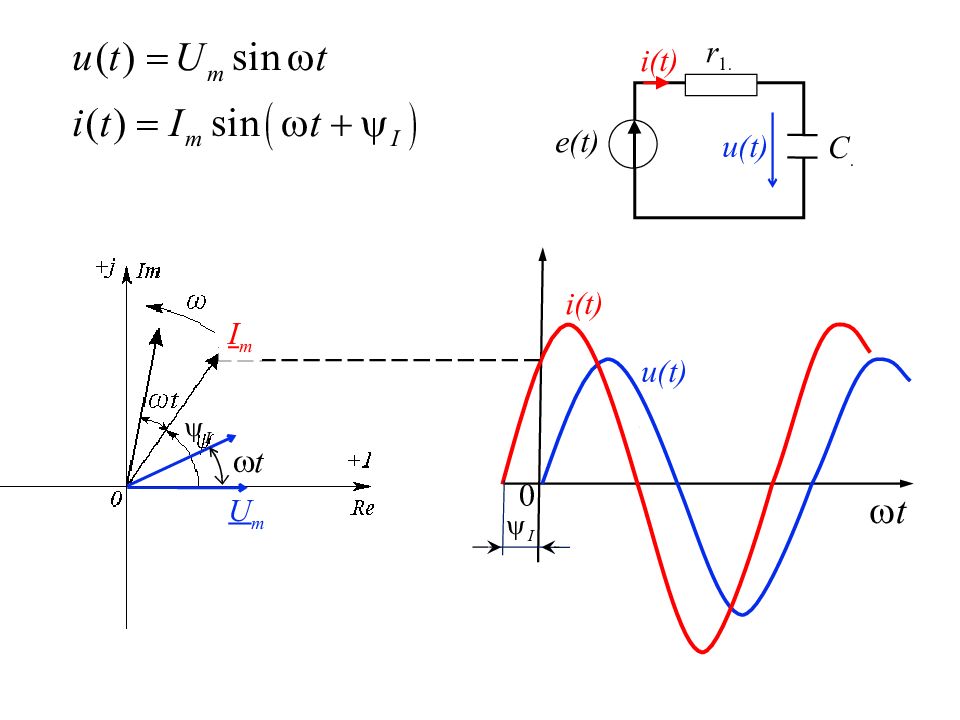
Мгновенное значение тока изображается на комплексной плоскости - комплексом амплитудного значения : или - комплексом действующего значения :
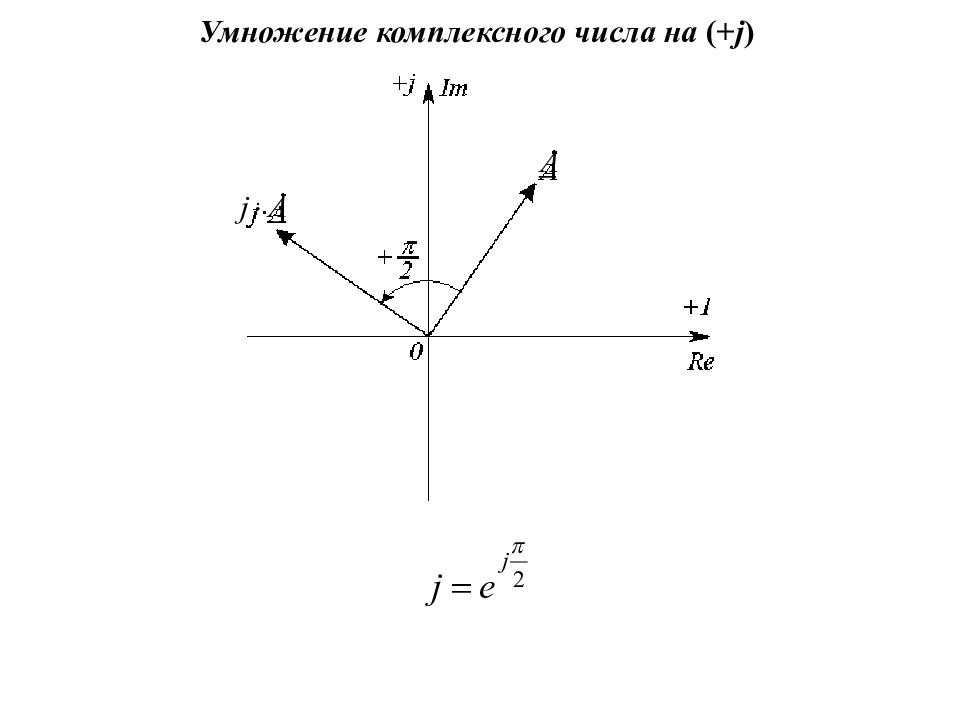
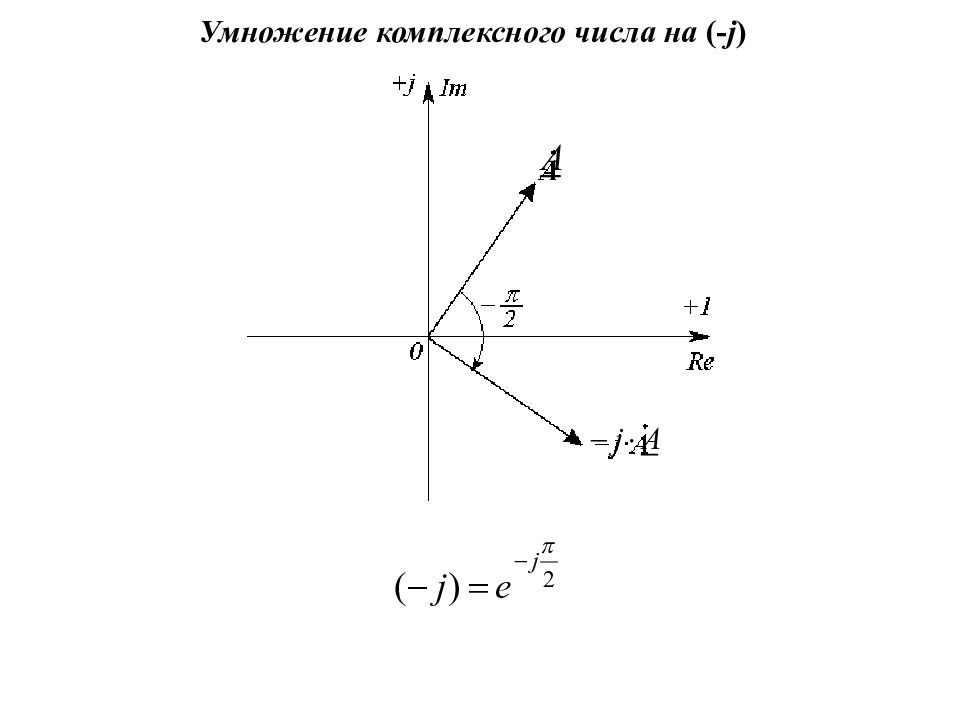
Пример Мгновенное значение тока: Комплекс действующего значения тока: Комплекс амплитудного значения тока: Im ( + j ) Re ( + ) Im ( + j ) Re ( + )
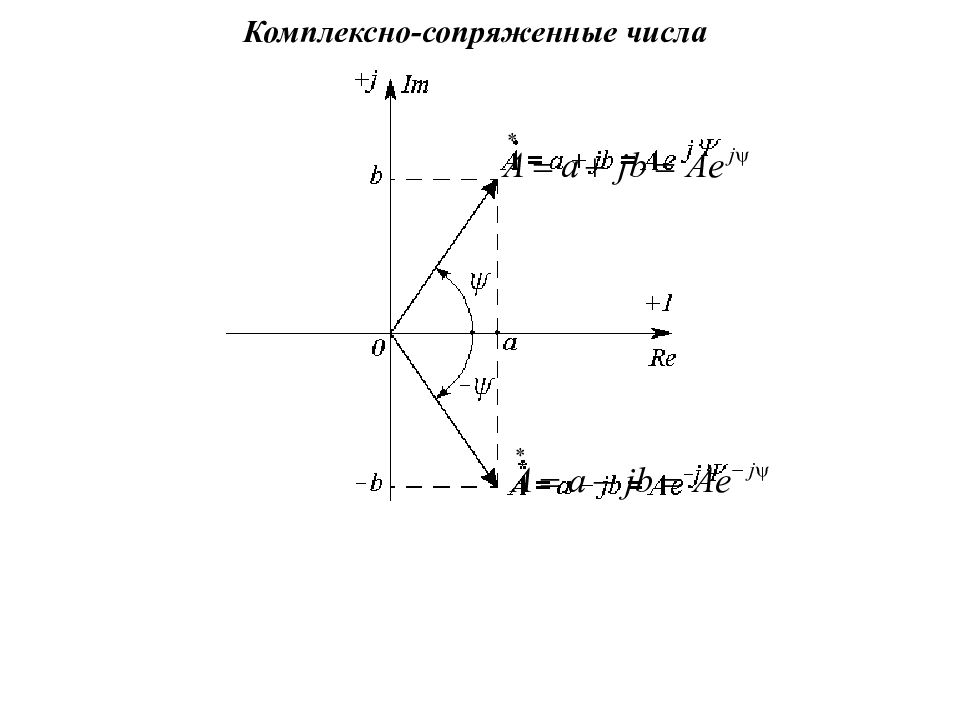
где a – действительная часть числа (координата по оси Re ); b – мнимая часть числа (координата по оси Im ). Алгебраическая форма комплексного числа Операции с комплексными числами
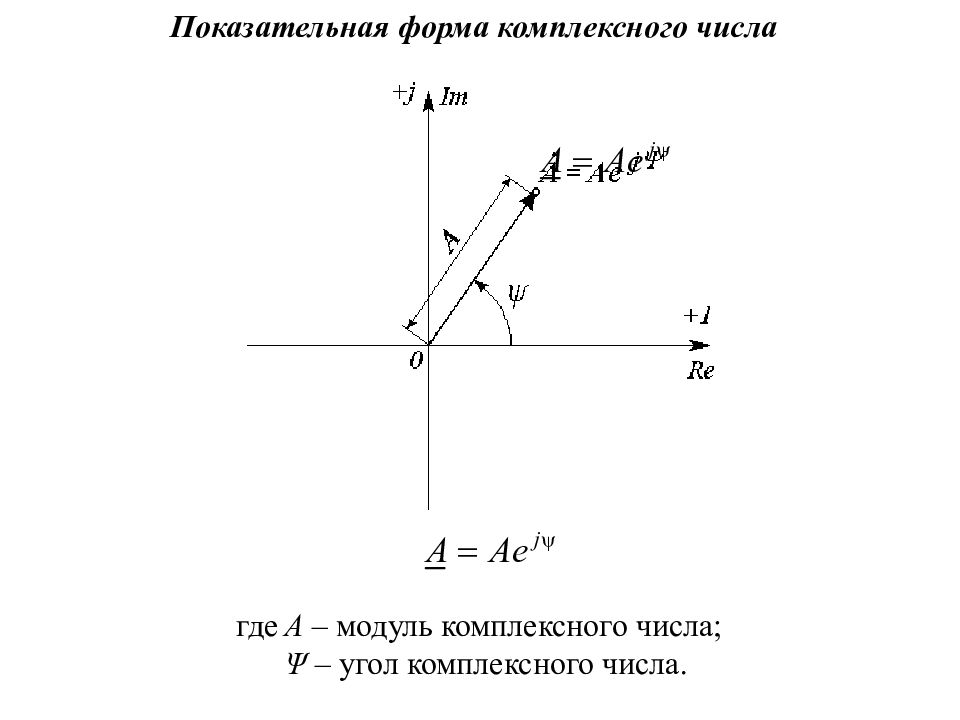
где A – модуль комплексного числа; Ψ – угол комплексного числа. Показательная форма комплексного числа
Т ригонометрическ ая форм а комплексного числа: Перевод из показательной форм ы в алгебраическую : Перевод из алгебраической форм ы в показательную :
Умножение комплексного числа на ( + j )
Умножение комплексного числа на ( - j )
Умножение комплексного числа на (-1 )
Перенос мнимой единицы из знаменателя в числитель
Комплексно-сопряженные числа
Комплексно-сопряженные числа
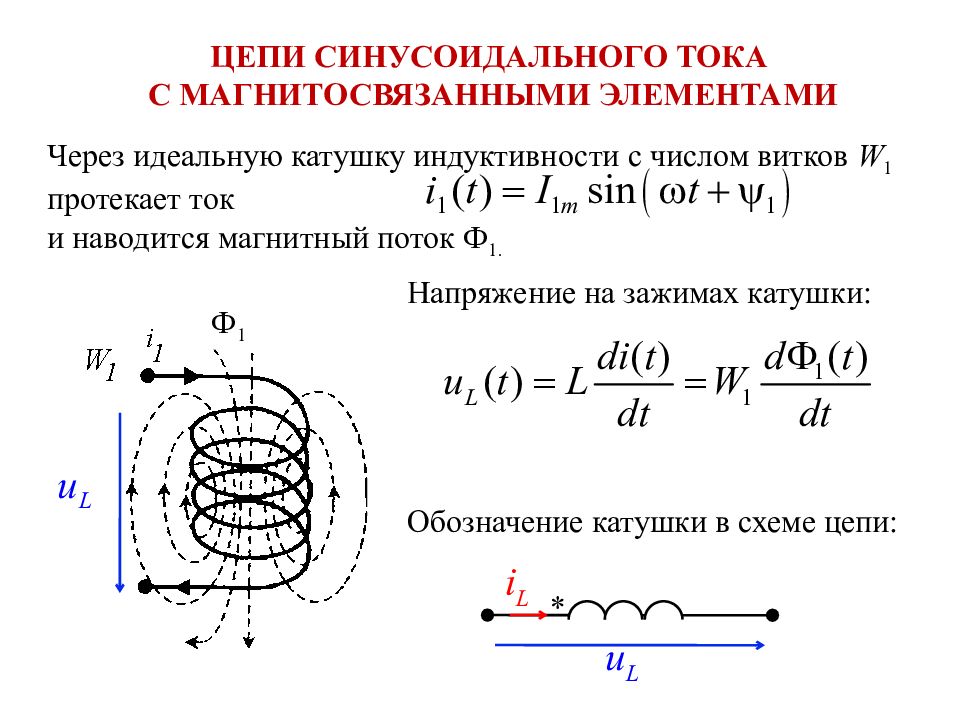
Найдем, как изображаются производная и интеграл синусоидальных функций с помощью комплексных чисел. СИМВОЛИЧЕСКИЙ МЕТОД РАСЧЕТА ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА Символический метода расчета цепей синусоидального тока основан на алгебраизации интегро-дифференциальных уравнений, записанных для мгновенных значений.
Дифференцирование синусоидальной функции:
Интегрирование синусоидальной функции:
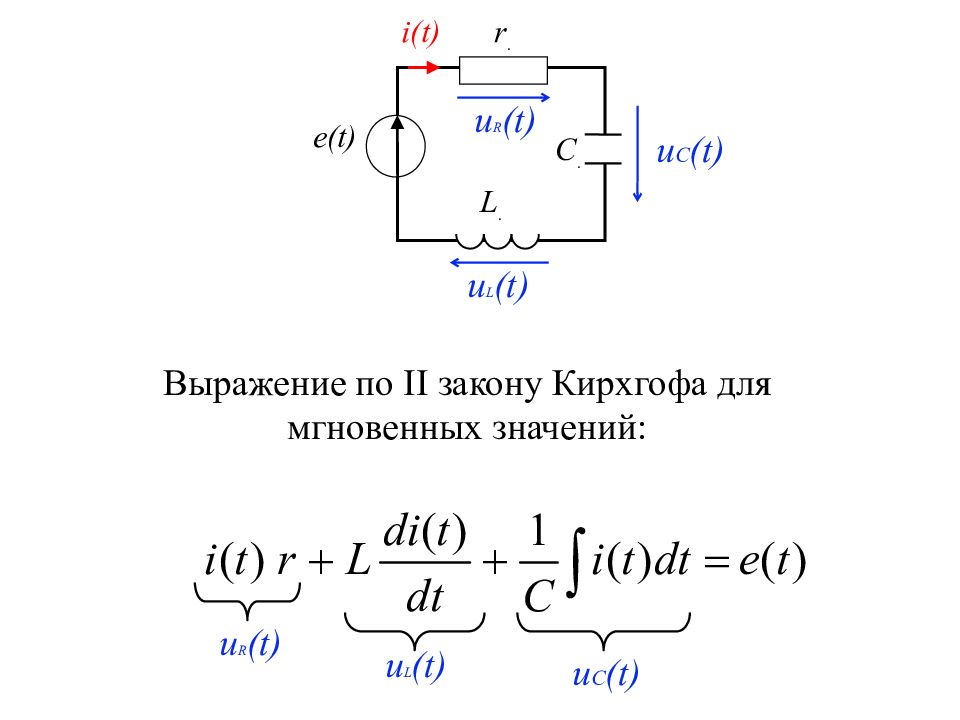
r. e(t) C. i(t) u C (t) L. u L (t) u R (t) u L (t) u C (t) u R (t) Выражение по II закону Кирхгофа для мгновенных значений:
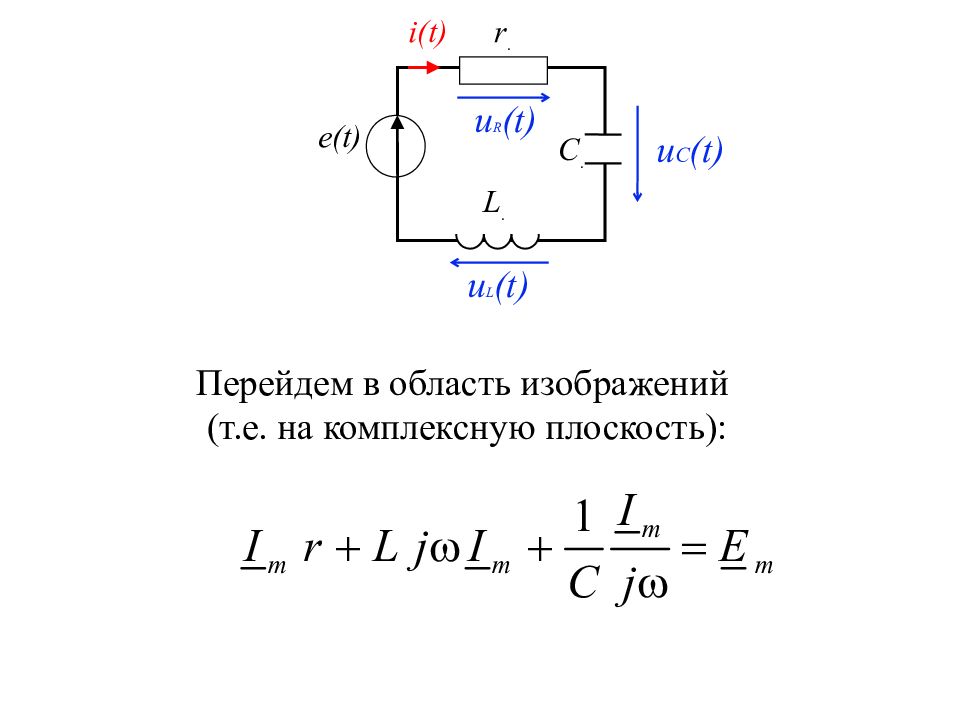
r. e(t) C. i(t) u C (t) L. u L (t) u R (t) Перейдем в область изображений (т.е. на комплексную плоскость):
Комплексное сопротивление:
где R – активное сопротивление; X – реактивное сопротивление. Модуль комплексного сопротивления называется полным сопротивлением участка цепи : Комплексное сопротивление: Комплексная проводимость: где g – активная проводимость; b – реактивная проводимость.
Треугольник токов Треугольник напряжений Треугольник сопротивлений
Закон Ома в символической (комплексной) форме Комплексное напряжение на участке цепи, не содержащем ЭДС, равно произведению комплексного тока на этом участке на комплексное сопротивление:
Законы Кирхгофа в символической (комплексной) форме Первый закон Кирхгофа : В любом узле электрической цепи сумма комплексных токов равна нулю. Комплексные токи, втекающие в узел, записываются со знаком « + », вытекающие из узла – со знаком « - ».
Второй закон Кирхгофа: В любом замкнутом контуре цепи сумма комплексных напряжений равна сумме комплексных ЭДС, включенных в контур. Комплексные напряжения и ЭДС, направления которых совпадают с выбранным направлением обхода контура, пишутся со знаком « + », не совпадают – со знаком « - ».
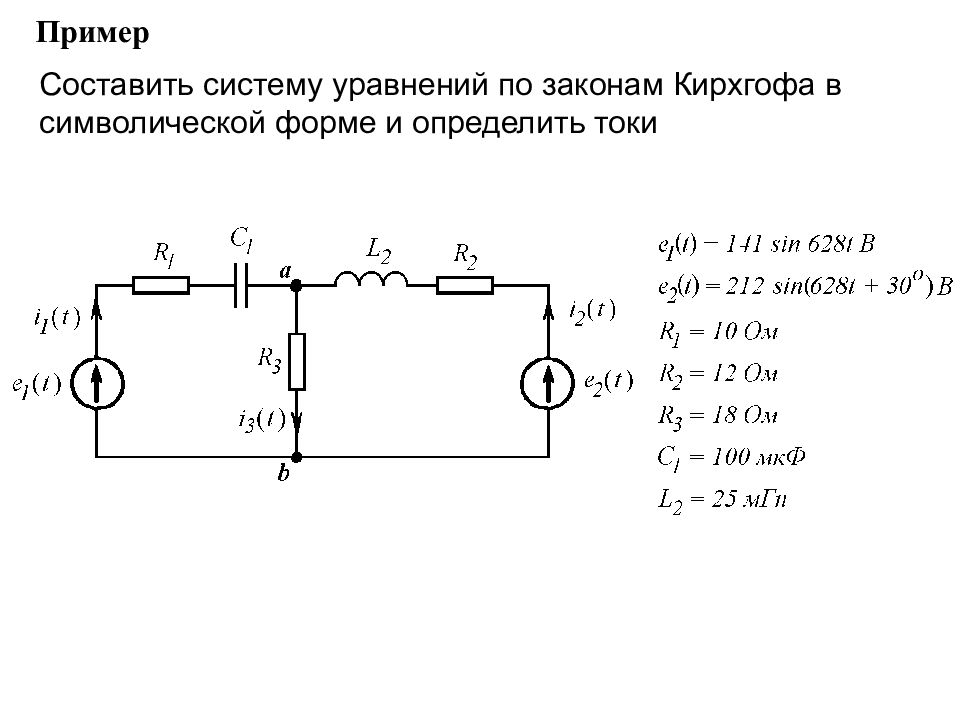
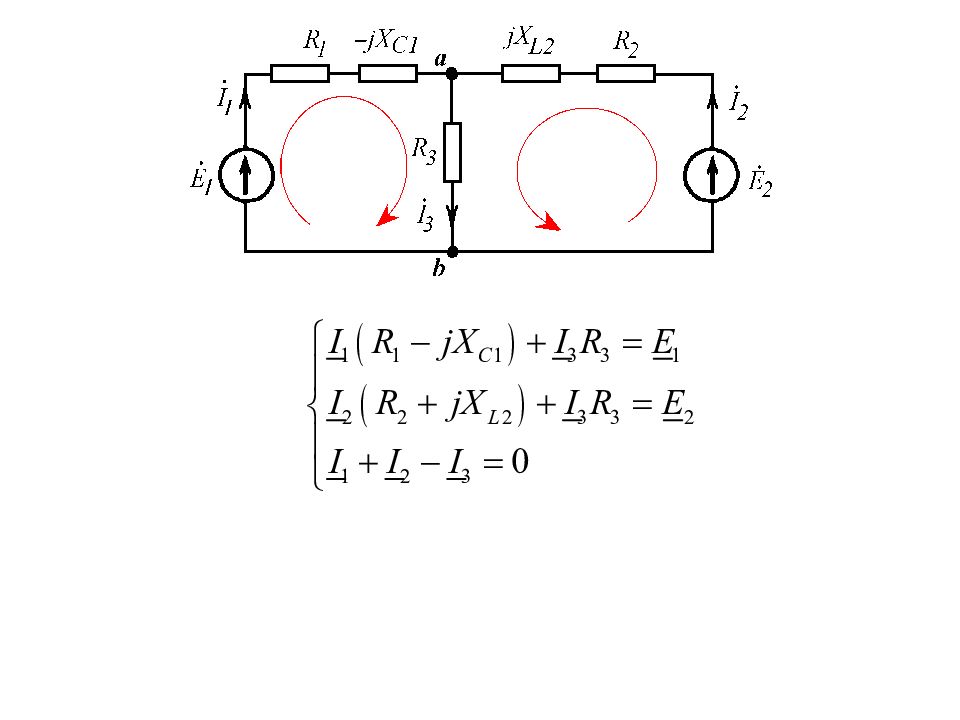
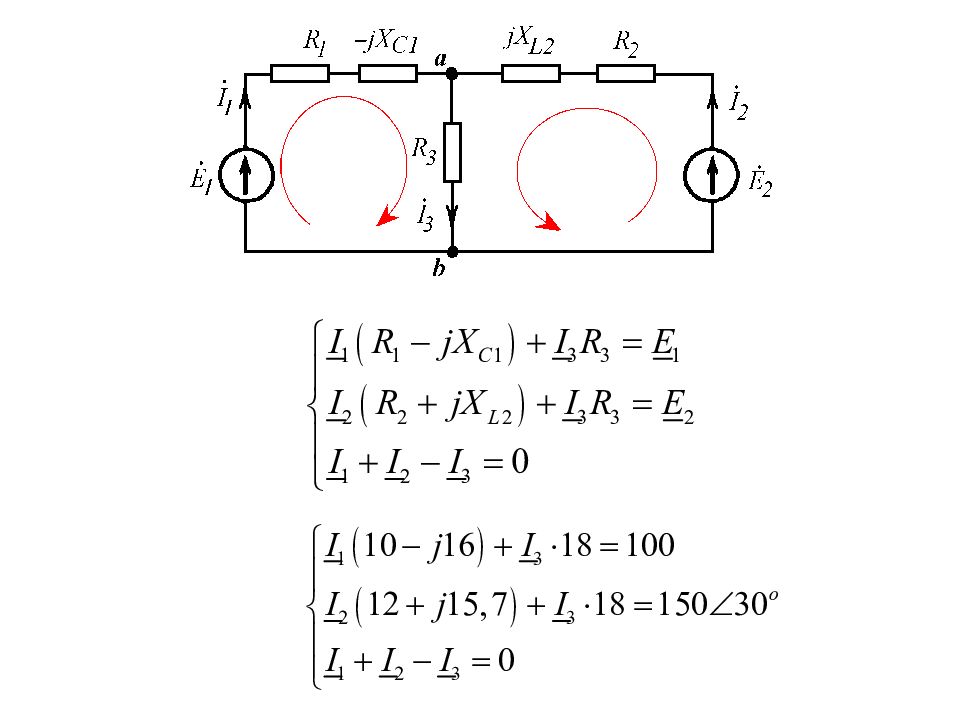
Пример Составить систему уравнений по законам Кирхгофа в символической форме и определить токи
Реактивные сопротивления: Комплексы действующих значений ЭДС: Решение:
Переход к мгновенным значениям токов:
Уравнения, составленные по законам Кирхгофа и Ома в символической (комплексной) форме представляют собой алгебраические выражения, аналогичные соответствующим выражениям для цепей постоянного тока. Все методы расчета цепей постоянного тока могут использоваться для расчета цепей синусоидального тока при условии применения символического метода.
МОЩНОСТЬ СИНУСОИДАЛЬНОГО РЕЖИМА
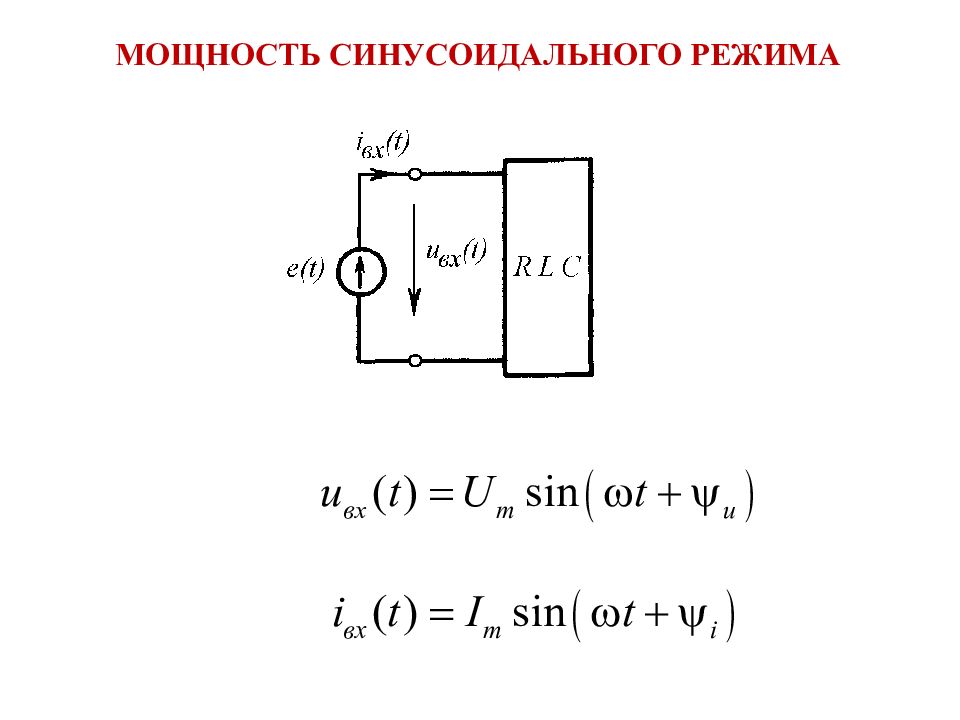
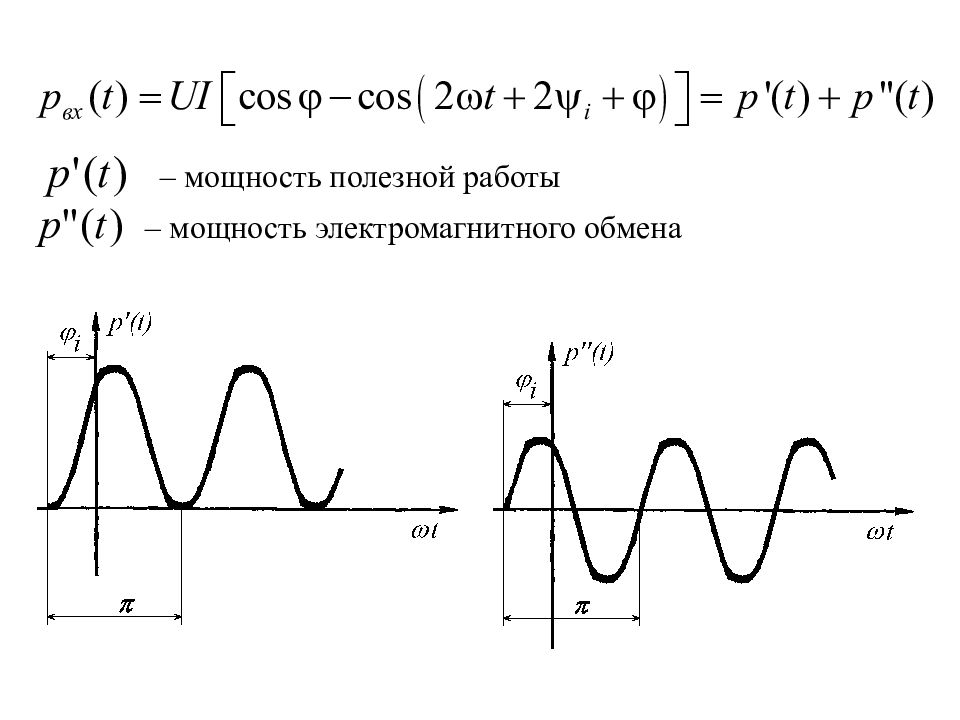
– угол нагрузки (угол между векторами напряжения и тока на комплексной плоскости)
– мощность полезной работы – мощность электромагнитного обмена
Реактивная мощность: Активная мощность:
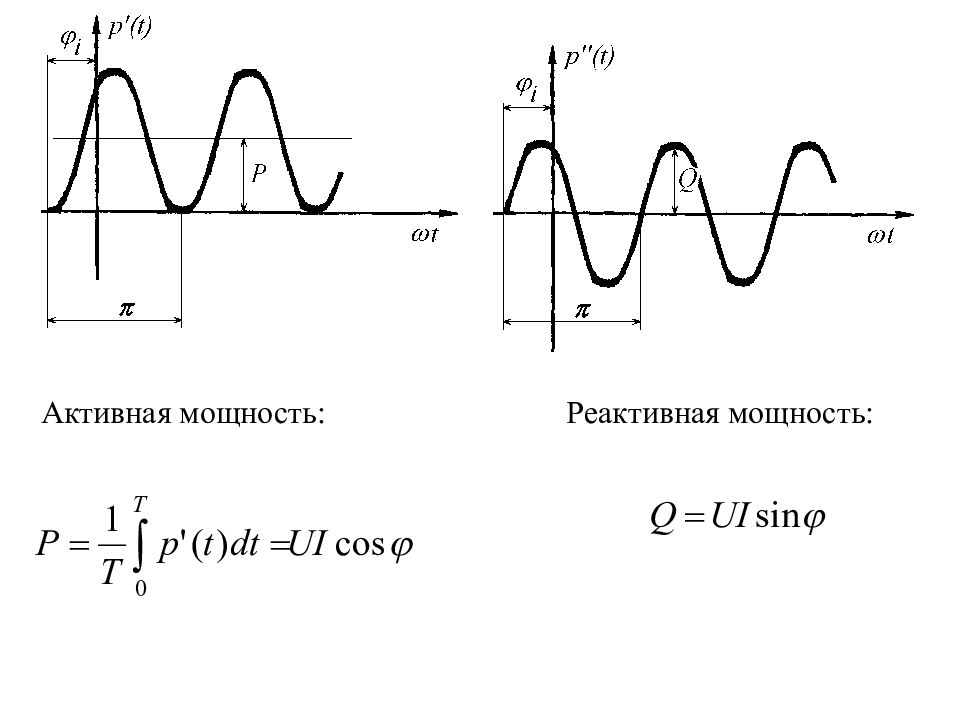
Баланс активной мощности: Баланс реактивной мощности: Полная мощность: Единица полной мощности – Вольт-Ампер ( ВА )
– коэффициент мощности
