Дано U={1;2;3;4;5;6;7;8;9;10;11}, A={1;2;3;7;9}, B={3;4;5;6;10 ; 11}, C={2;3;4;7;8}, D={1;7;1 1 }. Вычислить множества 1) 2) 3) 4) 5)
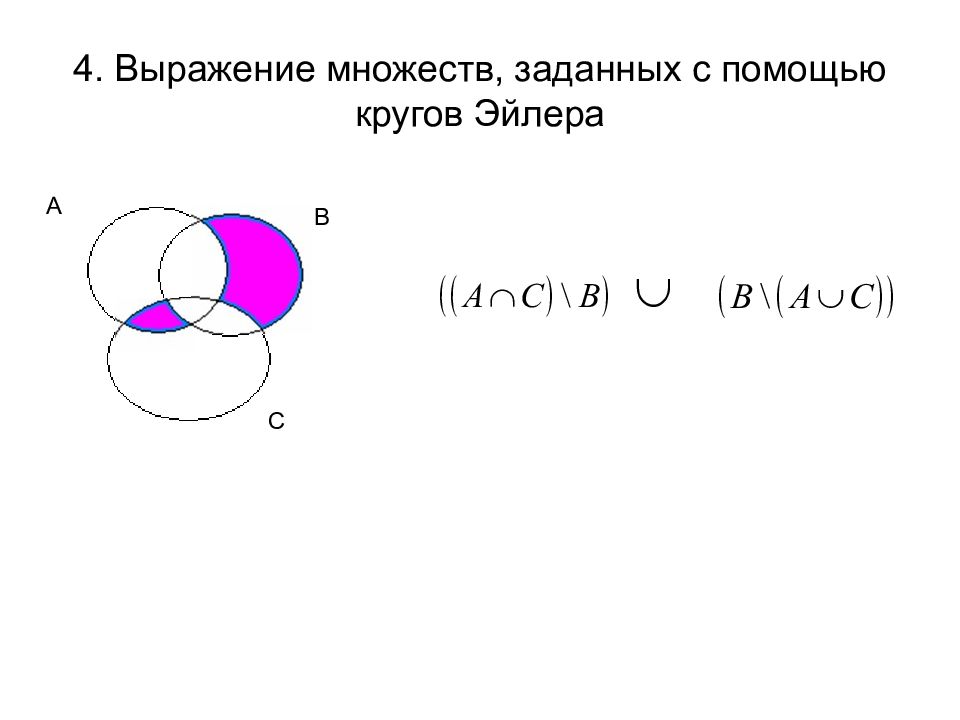
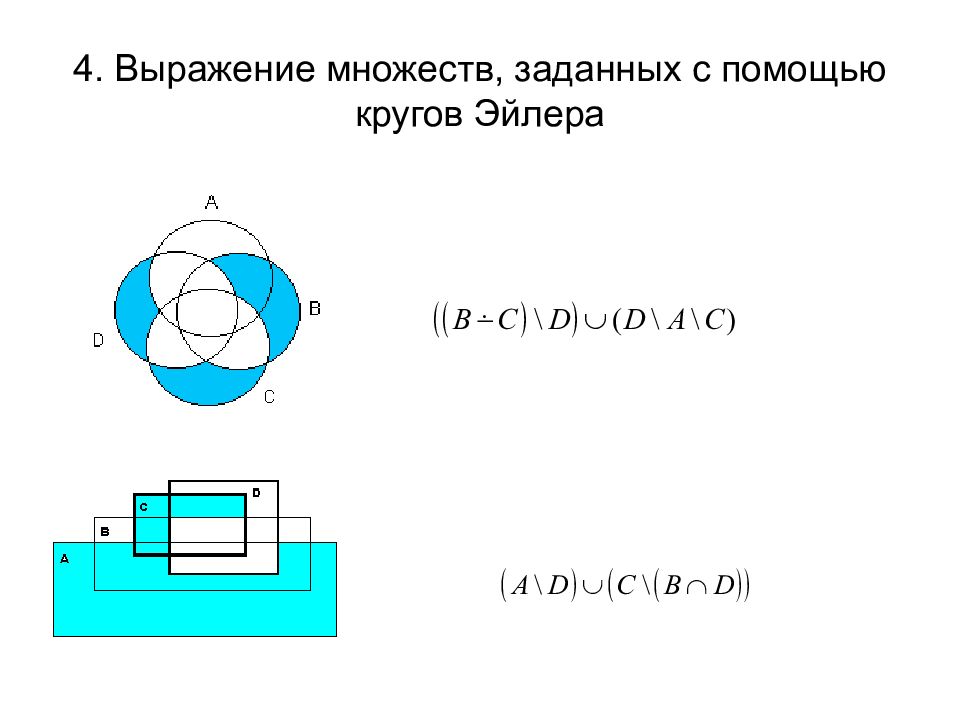
2. Выражение множеств Пусть U={1, 2, 3, 4, 5, 6, 7, 8,9}, A={1, 2, 3, 5}, B={2, 4, 6, 8}, C={1, 3, 5, 7}, D={4, 5, 7, 8}. Выразить через известные множества A, B, C, D следующие множества. {1,2,3,4,5,7,8}= {4, 7,8}= {2,5,6,7}= {2,5}= {5,7,9}= {4,5}= Невозможно выразить через данные множества, так как элементы 4 и 8 одновременно принадлежат или не принадлежат данным множествам.
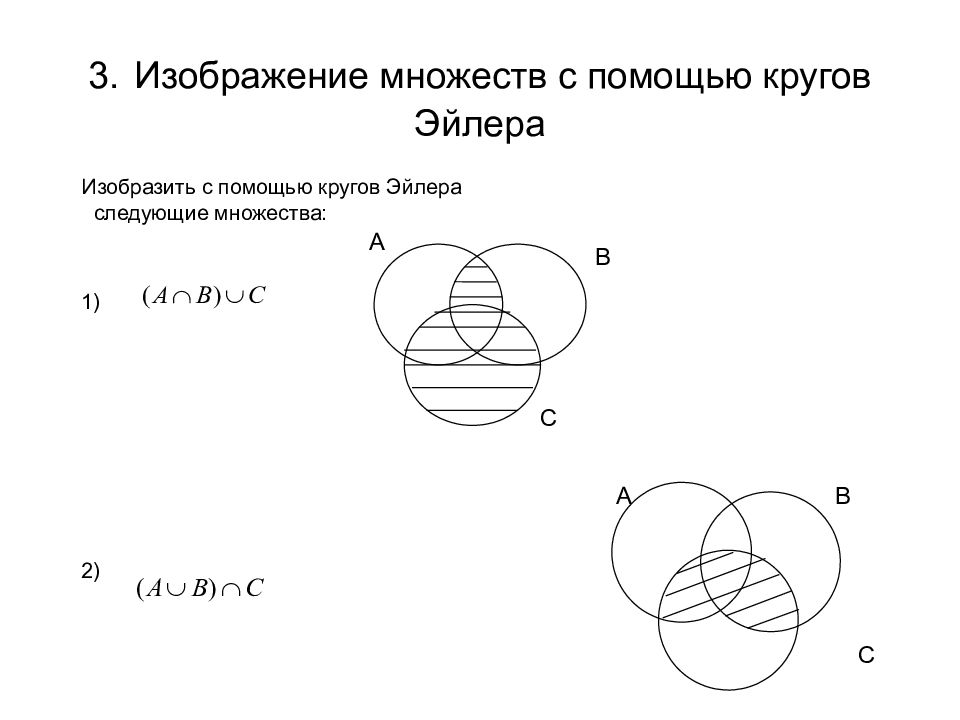
Изобразить с помощью кругов Эйлера следующие множества : 1) 2) A B C A B C
3) 4)
A B C
Декартово произведение Под упорядоченной парой (а; b) мы будем понимать двухэлементное множество, состоящее из элементов а и b, в котором зафиксирован порядок расположения элементов. Отметим два характерных свойства упорядоченных пар: 1) если 2) Определение 1 Декартовым произведением множеств А и В называется множество Пример Пусть A={1;2}, B={a, b, c}, тогда {(1;a);(1;b);(1;c);(2;a);(2;b);(2;c)} ; {(a;1);(b;1);(c;1);(a;2);(b;2);(c;2)}. Очевидно, что, вообще говоря,
Определение 2 а) Множество называется декартовым произведением n множеств; б) - (n cомножителей) – n-aя декартова степень множества А; Пример Пусть,, Тогда
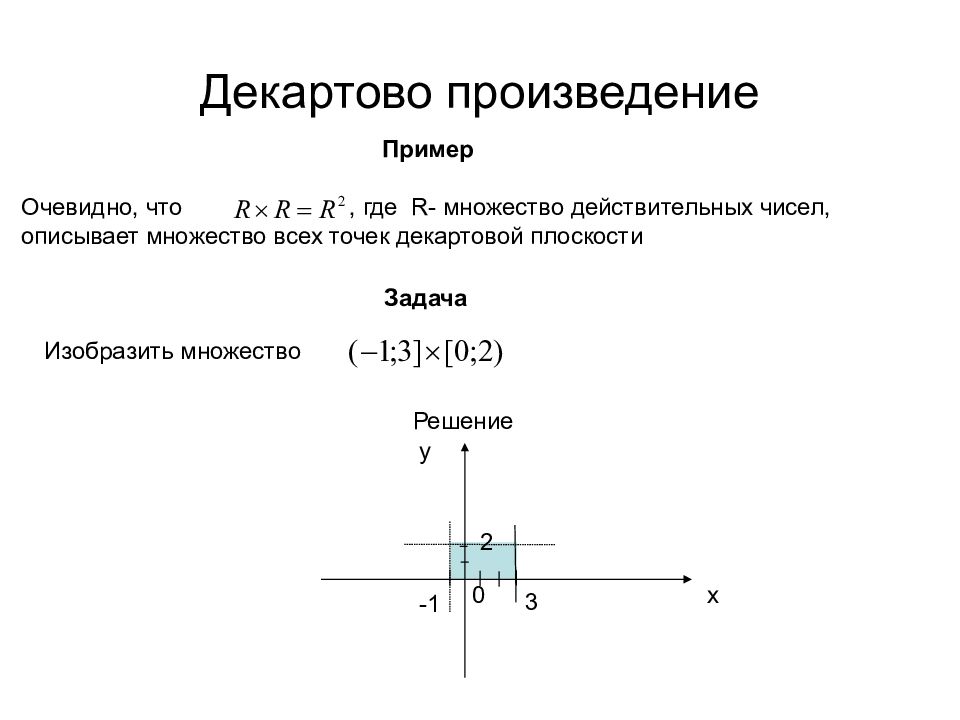
Задача Изобразить множество Пример Очевидно, что, где R - множество действительных чисел, описывает множество всех точек декартовой плоскости Решение -1 3 2 x y 0
Теорема 1 Пусть А, В, С – произвольные множества, тогда
Доказательство Декартово произведение Следовательно
Декартово произведение Доказательство Следовательно
Декартово произведение Доказательство Следовательно
Теорема 4 Если множество А состоит из m элементов, а В – из n элементов, тогда состоит из mn элементов. Доказательство ММИ по числу элементов множества B. n=1. то есть AB имеет m=m*1 элементов. 2) Допустим, что теорема верна при n=k. 3) И пусть теперь В состоит из к+1 элемента, то есть где Тогда, где поэтому множество АВ состоит из mk+m=m(k+1) элементов.
